磁轴承的遗传优化的变论域模糊PID 控制

孙志瑞，张艳兵，王慧芬

（1.中北大学 电气与控制工程学院，山西 太原 030051；2.中北大学 电子测试技术国家重点实验室，山西 太原 030051）

0 引 言

磁悬浮轴承以主动磁悬浮轴承为主，是一种对支撑部件很好的选择，如参考文献[1⁃3]描述它的优点是：可以使转子无机械接触，能够无摩擦转动，使转子的速度大幅度提升，能够达到40 000 r/min。参考文献[1]所述目前主要用在新能源领域的飞轮储能、机床等，在动力领域方面有离心压缩机、分子涡流泵等，通过对径向磁轴承、轴向磁轴承进行控制，达到其支撑的转子能够稳定悬浮并高速旋转，因此，对磁轴承控制算法的要求比较高。

当转子偏离中心位置时，磁轴承产生的电磁力也要发生相应的改变，使转子回到中心平衡位置，这就需要系统快速、准确地响应去满足此要求，因此控制器的选择很重要。目前参数、负载大幅度的非线性变化，使传统的PID 控制很难达到设计的理想初衷[1⁃2]。模糊PID控制因有一定的控制规则，导致对自我校正能力产生很大影响，在消除系统误差上表现很差，当系统趋于稳定时，易引起小范围震荡，难以得到很好的控制精度[3⁃4]。另外，变论域模糊PID 控制虽然通过对基础论域进行划分，对控制精度有一定的提高，但是规则数太多，不能快速地反映实时性。因此，本文通过利用遗传算法对控制器PID 参数值进行离线优化，将其作为在线调值的初值，再通过选用合适的伸缩因子，使基本论域随着控制需要自适应发生伸缩变化，从而提高控制的精度，降低超调，有很好的自适应能力。

1 磁悬浮轴承系统数学模型

单自由度磁悬浮轴承控制系统的结构如图1 所示。转子由左右两线圈相向配置通过励磁电流进行差动控制。位置传感器检测出转子相对于平衡位置产生的误差，将此误差送到控制器，经由事先规定的控制方法回到中心平衡位置所需的控制变量，将其送到功率放大器，经功率放大器产生足够大小的控制电流，使电磁铁产生相应的电磁力，从而使转子能够稳定悬浮。

图1 单自由度磁悬浮轴承控制系统结构图

在均匀气隙磁通，不考虑铁芯磁阻、漏磁的情况下，当转子偏离平衡位置时，经过传感器检测出转子偏离平衡位置的位移为l0，气隙分别为l+l0和l-l0，控制器通过转换电路将检测到变化，并将其转换成控制信号的形式输出，该信号被传输至功率放大器，经过一定处理生成控制电流i，i1=i0+i，i2=i0-i（i1，i2为激励电流）。

驱动电磁线圈产生电磁力之差为F=F1-F2，F1，F2的表达式分别如下：

当转子轴心有微小位移时，由牛顿第二定律得到转子的运动方程为：

用泰勒级数对式（1）在（i0，l）处展开，进行线性化后，可得：

对式（2）进行拉普拉斯变换，得到磁悬浮轴承转子的传递函数为：

2 遗传算法离线优化PID 参数初始值

针对PID 参数整定困难，常规控制器参数往往整定不良，所以选择了与一般整定PID 参数初始值有差异的方法，以遗传算法为基础的寻优对其实施离线优化。优化流程图如图2 所示。

图2 遗传优化PID 参数流程图

优化步骤具体如下：

1）遗传算法的初始步骤是以待优化参数取值范围为依据，生成相关参数组合；

2）经过仿真操作获取参数组合的系统误差，从而成功获取ITAE 指标数据；

3）将ITAE 传送至优化程序即可。

每个参数的编码长度由该参数的取值范围和搜索精度确定。本次研究选取二进制作为编码方式[5⁃7]，且的取值范围依次是[0，50]，[0，150]，[0，10]，图2中几个重要参数的设置情况如下：种群数n 设置为30，最大遗传代数Gmax设置为50，交叉概率Pc设置为0.8，变异概率Pm设置为0.001。个体适应度函数在遗传算法中起重要的作用，在个体的认可过程中作为一种评判能力，个体适应度函数形式如下[5]：

式中J 为ITAE 性能指标。

经由交叉、变异、持续搜索，最终寻找到控制器优化后的PID 初始参数值

3 变论域模糊PID 控制

3.1 变论域模糊PID 控制原理

该控制原理的核心思想在于模糊控制规则的不变性，根据误差及误差变化率的变化，引入一个伸缩因子使得初始模糊论域持续伸缩。如果误差变大，论域就会随之变大；反之，如果误差变小，论域就会随之而变小。这相当于在一个小范围内细分化了原有的控制规则，从而达到提升控制精度的目的[8⁃9]。

假设输入变量的初始论域为[-E,E]，伸缩因子为α(x)，通过不断伸缩改变论域的大小，得到伸缩之后的论域为[-α(x)E,α(x)E]，因此，根据系统需求，通过伸缩因子不断调整初始论域，达到改变论域的目的[10]。

3.2 变论域模糊PID 控制器设计

变论域模糊PID 控制的主要内容是借助于一定条件对论域大小进行伸缩调整，从而满足多种控制器参数的范围和精度要求，根据系统需求的变化进行调控，实现系统的稳定运行。参考文献[11]采用函数形式表达论域伸缩因子，函数模型如下：

式中λ ∈(0,1)，k>0。

考虑到伸缩因子选择的合适与否对控制效果有着较大的影响，因而将伸缩因子的选取作为评价变论域模糊PID 控制器功能高低的准则，从而构建基于遗传算法的变论域模糊PID 控制器，其结构框图如图3 所示。

图3 控制结构框图

图3 中模糊控制器为基于误差e 及误差变化量ec 的PID 增益调整型控制器，控制过程如下：

1）经过误差e 及误差变化量ec 根据伸缩因子函数模型得到输入变量e，ec 的伸缩因子，然后经过变论域模糊推理得到输出变量Δkp，Δki，Δkd的伸缩因子βpid。

2）通过分别调整模糊控制器的量化因子ke，kec和比例因子Lm，m=p,i,d 实现输入输出变量论域的改变。

3）在线整定参数kp，ki，kd以提升系统控制能力的精度。

3.3 系统参数及规则设定

在进行一定量的实验和调试之后，获取输入变量的两个重要指标数据，即位移偏差e 和位移偏差变化率ec，它们的论域范围是[-0.3，0.3]和[-6，6]，而Δkp，Δkd，Δki这3 个输出变量的论域范围是[-3，3]，[-0.6，0.6]，[-3，3]。另外，根据伸缩因子的函数模型（见式（6）），取λ=0.6，k=0.5，可得到输入变量e，ec 的伸缩因子，输出变量Δkp，Δkd的伸缩因子具有与误差的单调一致性，而Δki的伸缩因子的特征与误差具有单调反向性关系，因此，其论域的伸缩因子需要实现Δkp，Δkd较大[12⁃14]，而Δki较小的输出结果，所以Δkp，Δkd，Δki的伸缩因子设置状况如下所有变量的模糊论域取{-6，-5，-4，-3，-2，-1，0，1，2，3，4，5，6}，也就是{NB，NM，NS，ZO，PS，PM，PB}，它们的含义则是以零为中介点，左边代表负大、负中、负小，右边代表正小、正中、正大[15]，其中隶属度函数均采用三角形函数。再者，控制系统按照Mamdani 模糊推理法合成规则，其中，变论域模糊PID 控制只是在模糊PID 控制前面增加了一个对基本论域进行伸缩的过程，实现模糊变论域的调整，模糊PID 参数调整算式为其中为经遗传算法优化的PID 三个初始值，Δkp，Δkd，Δki为模糊控制器的输出，也就是PID 的调整值。

4 系统仿真结果及分析

磁悬浮轴承对转子控制实现稳定悬浮，在Matlab 中的Simulink 搭建仿真图进行仿真分析。

仿真中各参数取值如下：磁悬浮转子的质量为150 kg，位移刚度系数δ2=2.6×106，电流刚度v=129，N=80，s=3.61×10-2m2，l0=0.03 m，量化因子ke=30，kec=0.75，比例因子Lp=0.5，Ld=0.5，Li=0.1。将参数代入式（4），得到控制系统的传递函数为

在Matlab 中的Simulink 进行仿真，仿真结果如图4所示。图中共有3 条曲线，在高峰位置最高的曲线代表的是模糊PID 控制，最低的曲线是遗传算法⁃变论域模糊PID 控制，而中间的曲线是变论域模糊PID 控制。

由图4 可知：模糊PID 控制在约0.14 s 处达到稳定，超调约为10%；变论域模糊PID 控制比前者控制有明显的提高，系统0.11 s 进入稳定，超调大约为6%；而经遗传优化的变论域模糊PID 控制系统约在0.02 s 处达到稳定，可以快速地调节使轴承转子回到稳定平衡位置，更能满足系统的响应需求。因此所设计的经遗传优化的变论域模糊PID 控制更好地改善了控制性能。

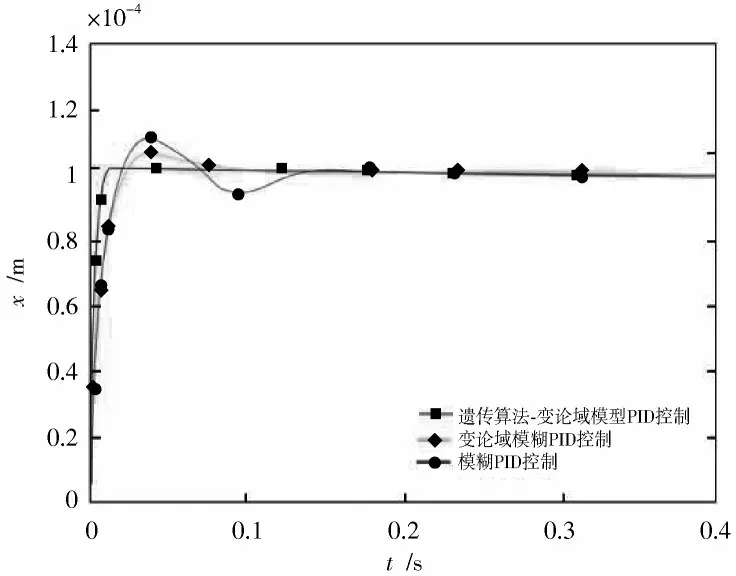
图4 主动磁悬浮轴承位移响应曲线

系统在0.18 s 处突然加一个扰动，改变负载时，通过仿真图5 可以看出，本文提出的控制算法对磁悬浮轴承的控制具有较强的自适应能力，系统响应速度快，约用时0.03 s 恢复到稳定。

图5 系统在0.18 s 处加扰动仿真图

5 结 论

磁悬浮轴承的转子在高速运转状态下，其系统具有很强的非线性，因此对控制器的要求很高。本文根据主动磁悬浮轴承的特性分析，结合变论域模糊控制、PID控制的特点，设计了经遗传优化的变论域模糊PID 控制器，使得系统有很好的动静态特性，提高了系统的响应速度，稳定性达到了要求，满足实验特性，具有很强的适应性。