碳纳米管增强水泥基复合材料的二维代表单元研究

吴正昊 应黎坪 杨宏明 彭一江

摘 要：为了从细微观尺度上研究碳纳米管-水泥基复合材料的损伤破坏过程和破坏机理，从碳纳米管-水泥基复合材料中选取尺寸为100 μm×100 μm的代表单元，建立二维代表单元的细微观层次的数值模型。以势能原理的基面力元法为理论基础，对代表单元进行数值模拟，探究在单轴受压状态下碳纳米管-水泥基复合材料的力学性能变化，并绘制破坏裂纹的发展过程图和最大主应力分布变化过程图。结果表明，该代表单元模型能够较真实地模拟复合材料在单轴压缩状态下的损伤破坏过程，通过数值模拟不同含量的复合材料代表单元模型，发现增强体的含量影响着复合材料的强度及韧性，选择合适的含量范围有利于提升材料的力学性能。通过数值模拟的方法分析碳纳米管增强水泥基复合材料的作用机理，拓展了基面力元法的应用范围，节约了计算资源，其结果丰富了碳纳米管-水泥基复合材料力学性能的研究，可为相关工程应用及基础研究提供参考。

关键词：复合建筑材料;碳纳米管;代表单元;基面力元法;数值模拟

中图分类号：TU529.0 文献标识码：A

doi： 10.7535/hbgykj.2020yx04001

文章编号：1008-1534（2020）04-0211-07

Abstract：In order to study the damage process and failure mechanism of carbon nanotubes reinforced cementitious composites on the micro scale， a representative volume element with the size of 100 μm×100 μm was selected from the composites to establish the numerical model of two-dimensional representative volume element at the meso-and micro-scales. According to the theory of the base force element method based on potential energy principle， a representative volume element was simulated to investigate the change of mechanical properties of carbon nanotubes reinforced cementitious composites under the uniaxial compression and draw the charts of the failure processes and the maximum principal stress distributions. The results show that the model can truly simulate the damage and failure processes of composite materials under the uniaxial compression. Through the numerical simulation of the representative volume element models of composites with different carbon nanotubes contents， it is found that the content of enhancement has an effect on the strength and toughness of composites， and choosing the appropriate content range is conducive to improve the mechanical properties of the materials. By means of numerical simulation method， the mechanism of carbon nanotubes reinforced cementitious composites is analyzed， which is beneficial to the expansion of the application scope of base force element method and the saving of computing resources. The results enrich the study of mechanical properties of carbon nanotubes reinforced cementitious composites， and provide a reference for relevant engineering application and basic research.

Keywords：composite building materials; carbon nanotubes; representative volume element; base force element method; numerical simulation

21世纪以来，水泥基复合材料逐步成为建筑工程领域应用最广、用量最大的工程材料，用戶对水泥基复合材料的要求越来越高。因此，对高性能水泥基复合材料的研究是材料领域的研究热点。吴中伟院士[1]为了改良水泥基材料抗拉、抗折性能较弱的力学特性，在材料中混合加入纤维以达到增韧的效果。然而，水泥基材料中的内部缺陷多为纳米尺度，故添加一些纳微级的增强体制成复合材料，可以更好地达到增强、阻裂、增韧等方面的目的。在纳微级纤维材料不断发展的今天，碳纳米管因其高弹模、大长径比等特点，被越来越多的学者深入研究并应用。对于碳纳米管与水泥基复合材料的研究尚处于试验探索阶段，特别是数值模拟分析及增强、增韧机理研究还处于起步、摸索阶段。

目前，在碳纳米管增强水泥基复合材料方面的研究成果相对较少，且以试验为主。MAKER等[2]通过声波降解、蒸发研磨，最早测得了碳纳米管-水泥基复合材料的弹性模量和强度。TRETTIN等[3]在高强混凝土中加入多壁碳纳米管，使其力学性能显著提升。为了改善水泥砂浆内部孔隙，LI等[4]使用质量分数为0.5%的多壁碳纳米管作为增强相来密实复合材料，增强后其抗压、抗折强度分别提升了19%和25%。徐世烺等[5]将质量分数为1.5%的多壁碳纳米管作为增强相掺入M140砂浆，以羟基化分散剂和水分散剂作对比，观察其增强效果。当以水为碳纳米管的分散剂时，复合材料的抗压、抗折强度分别提高了15.9%和20.7%。

在碳纳米管-水泥基复合材料的损伤机理方面，TAN等[6]通过微观试验发现因多壁碳纳米管在水泥浆体中的纳米填充作用，有效地改善了原先水泥基材料的孔隙率。陆富龙[7]使用多站全自动比表面积及孔径测试系统测定复合材料中孔的数量及分布，并利用热重分析和X射线衍射测试水化产物的力学性质，发现水化产物减少了内部的裂缝。牛荻涛等[8]和刘巧玲等[9]分别对碳纳米管的影响进行系统性分析，发现增强体在结构中起到桥联作用，通过电子显微镜进行细微观观察，发现主要增韧机理为拔出及脱粘作用。

研究表明，利用纳米结构与宏观结构的某些相似性，采用连续介质力学的基本理论进行唯象分析，是非常有效的方法。在材料性能研究领域，由于分子动力学和量子力学所需计算存储空间较大、占用的计算资源较多，其逐渐被基于连续介质力学的有限单元法所取代。在材料细微观研究中，WAN等[10]建立基于连续介质的有限元模型，针对加载过程中的应变能的变化，选取长度不同的单壁纳米管，研究其增强复合材料的载荷传递机理。姚小虎等[11]在分析单壁碳纳米管在纯弯和轴压情况下的变形问题时，采用有限元的方式进行建模，并用分子动力学进行了验证，通过对比证明了在碳纳米管细微观中应用有限元法的正确性。

2003年，GAO[12]提出基面力的概念，并在空间三维体系中以显式表达式的方式，给出任意多面体单元的刚度、柔度矩阵。基于连续介质力学理论，彭一江[13]提出新型有限元方法-基于势能原理的基面力元法。2014年，基面力元法被应用在再生混凝土的细观研究中[14-15]。PENG等[16]成功将基面力元法应用于再生混凝土三维损伤问题中。随后，孟德泉等[17]、崔云璇等[18]、杨欣欣等[19]不断扩大基面力元法的应用范围，分别在不同应变率下的随机骨料模型、细观等效模型中进行模拟，还结合图像处理技术对真实骨料进行细观分析。

本文基于势能原理基面力元法，在细微观尺度上建立碳纳米管-水泥基复合材料代表单元（representative volume element， RVE）模拟单轴受拉试验。在细微观尺度上，绘制应力-应变全曲线，并探求缝纹演变及其延伸规律，以及碳纳米管材料在复合材料中起到的增强增韧作用机理。本研究拓展了基面力元法的应用范围，节约了计算资源，为在细微观尺度上研究碳纳米管-水泥基复合材料提供了新的方法。

1 数值模型

1.1 势能基面力元法

势能原理基面力元法较之常规有限元方法，在求解过程中不需要进行积分，可以减少对能量方程求积分的计算过程，节约了计算资源。单元刚度矩阵是有限元方法的核心，本文采用三角形基面力单元[20]，如图1所示。

1.2 损伤本构模型

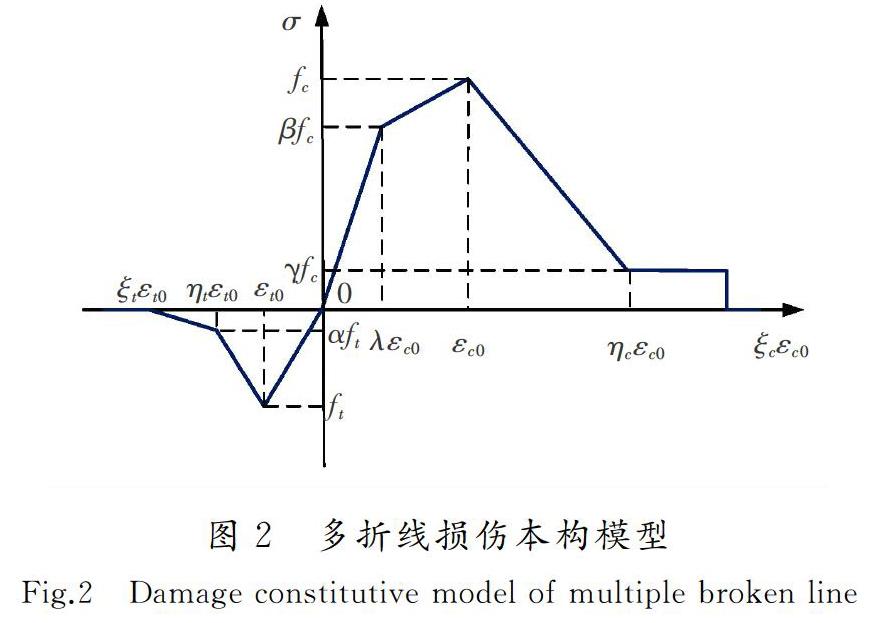
在临近压应力峰值时，水泥基材料呈现出较为明显的非线性特征。因此，基于双折线损伤本构模型，本文中的水泥基材料使用多折线损伤本构模型，如图2所示。

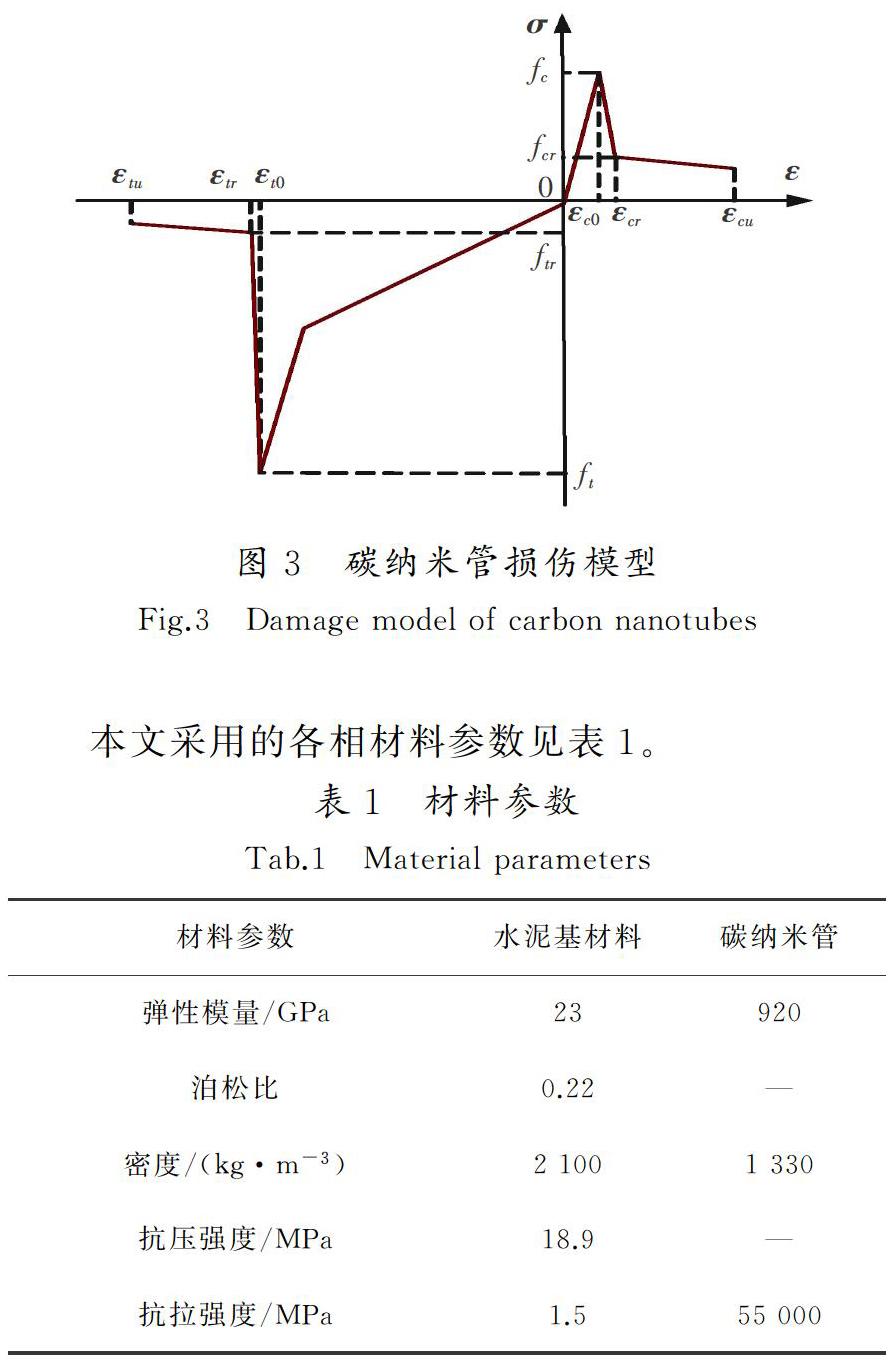
根据分子动力学模拟[21-22]得到的轴向拉压与压缩的应力-应变关系，通过名义应变-应力与真实应力-应变的转换，可得到碳纳米管损伤模型，如图3所示。

本文采用的各相材料参数见表1。

1.3 二维代表单元模型

完整的复合材料细观模型包含大量力学性能差异较大的增强相、基体等，分析材料整体力学性质时，完整模型的计算量过大。因此，根据均匀化的思想，假设复合材料为一个周期性的均匀材料，引入一个合适的单位微元体，称之为代表单元体。将真实非均匀的复合材料转化成均质化的材料，在此基础上展开计算分析，大大节约了计算资源和计算时间，并保证了计算值的精确度。

在建立二维代表单元模型时，首先选择合适的单元尺寸。當代表单元体的尺寸与夹杂相的尺寸之比达到6及6以上[23]时，其力学性能的计算结果保持稳定。本文选取的碳纳米管长度为15 μm，代表单元体尺寸为100 μm×100 μm，这时的代表单元体尺寸与夹杂相尺寸的比值为6.67。碳纳米管的位置坐标和角度由蒙特卡罗法产生的随机数确定，投放到代表单元中。使用Fortran编译程序里QuickWin图形显示模块编译绘图软件，投放过后代表单元图如图4所示。本文选用三角形单元网格剖分，并使用单元映射的方法进行单元属性的判定。

2 数值模拟

2.1 加载模型

在单轴静态压缩条件下，本文所建立的代表单元的加载模型如图5所示。在数值模拟时，底部边缘的节点全部进行竖向位移约束，底部中心节点进行水平位移和竖向位移2个方向的约束。二维代表单元模型的尺寸为100 μm×100 μm，加载方式为均布位移逐级加载，加载步长取0.005 μm/加载步。选取的代表单元中碳纳米管的含量为0.2%（体积分数，下同）。

2.2 试验对比

为了验证代表单元模型的有效性，本文选取相同掺量的复合材料，与高良丽[24]的压缩试验结果进行对比。根据短纤维增强的强度理论，则复合材料的平均应力为

式中：σc为复合材料中碳纳米材料的平均应力;σm为水泥基材料中的应力;cc为碳纳米管材料在复合材料中的体积比;cm为水泥基材料在复合材料中的体积比。在单轴压缩过程中可视为整个单元模型的平均应变为ε，则根据复合材料力学计算公式[25]，可得：

式中：V为复合材料的体积，在二维模型中可视为面积;σk为第k个单元的轴向应力;εk为第k个单元对应的应变;Vk为第k个单元的面积。对应力-应变曲线进行无量纲化，以σ/σ0为纵坐标轴，以ε/ε0为横坐标轴，绘制试验和数值模拟的无量纲的应力-应变曲线（见图6）。

从图6可以看出，在峰值应变前，本文建立的模型与试验所得的曲线的发展趋势一致;当达到峰值应变后迅速发生破坏，应力极速下降，且对下降趋势的描述较为一致。比较的结果验证了代表单元模型的准确性。

2.3 數值模拟结果分析

图7展现了代表单元破坏过程及破坏裂纹的发展过程。由图可知，破坏单元最开始出现在碳纳米管与水泥基体交界处。随着加载的进行，裂纹和破坏单元逐渐发展增多，并沿着基体交界处发展。因为代表单元模型受到的是竖向受压荷载，因此纵向或偏纵向分布的碳纳米管周围单元最先出现破坏，并且破坏发生的最快;而横向或偏横向分布的碳纳米管单元因其与加载荷载相互垂直，起到联结作用，其周围单元不易发生破坏，并且因碳纳米管单元强度高、弹模大，故未发生破坏，并且帮助周围单元分担部分应力，从而周围被破坏的单元较少。此过程与图7所显示的破坏过程一致。已发生破坏的单元无法继续传递应力，故图中所描述现象切合实际情况，证实了数值模拟的加载破坏过程的合理性和正确性。

图8展现了不同加载步时，模型的最大主应力分布。由图可知，数值模拟初期，因为碳纳米管与水泥基材料材性差别较大，已出现应力分布不均匀的现象。随着加载的进行，应力分布不均匀的程度加剧，碳纳米管与水泥基材料的结合处为相对薄弱处，发生应力集中现象，开始出现被破坏的单元。应力伴随着破坏发生重分布，破坏单元两侧的单元可承受应力降低，裂纹破坏加宽加大，裂纹主要方向为斜侧45°。加载继续进行，破坏单元区域相互连接起来，发生合并贯穿现象，材料逐渐失效，最终导致模型破坏的发生。通过应力分布图，可以较为清晰地看出增强相附近区域的应力较大。在受压过程中，碳纳米管单元承担的应力较大，起到增强复合材料的作用。因此在制备复合材料时应当充分将增强体均匀分散，以达到最有效的力学性能。

3 碳纳米管含量的影响

为了进一步探究碳纳米管含量对于复合材料强度的影响，分别选取0.1%，0.2%，0.3%，0.4%，05%的5种不同碳纳米管含量的复合材料模型，进行单轴静态压缩模拟。基于上述建立的二维代表单元损伤分析程序进行损伤计算和机理分析。

图9为单轴静态压缩条件下，5种不同含量的碳纳米管的复合材料代表单元的应力-应变曲线。不同的复合材料二维代表单元的计算数值（包括峰值压应力、应力提高率的具体数值）如表2所示。

可以从图9中较为直观地看到，当碳纳米管含量为0.2%时复合材料的抗压性能最强。与普通水泥基材料对比，强度提升了27.22%，说明增加碳纳米管的含量后，对水泥基材料的抗压性能有明显的增强作用。应力峰值随着碳纳米管含量的不同而发生改变，且碳纳米管含量存在最佳值。在本模型中，最佳含量值应处于0.1%～0.3%。当碳纳米管含量小于最佳值时，其抗压强度和抗压性能随着含量的增大而增大;当碳纳米管含量大于最佳值时，其抗压强度和抗压性能随着含量的增大而减小。

通过上述模拟，发现碳纳米管的增强效果与其含量有关，但是复合材料的强度并没有随着碳纳米管含量的增加而一直增加，证明了复合材料在增加增强相含量时，存在最佳取值范围。在复合材料中，碳纳米管表面包裹着羧酸化形成的水化物，因此两者交界处的作用力主要是化学作用力，起着桥联的作用。当出现局部断裂时，由于拔出作用，分担了大部分外力，消耗了大量能量。同时，碳纳米管的掺入发生了纳米充填作用，大大降低了复合材料中的孔隙率，改善了部分孔结构，使水泥基材料在细微观下的结构更为致密。

4 结 语

通过对碳纳米管-水泥基复合材料二维代表单元模型进行单轴静态压缩的数值模拟，得出以下结论。

1）碳纳米管-水泥基复合材料二维代表单元模型，能较准确地反映出代表单元在加载过程中破坏裂纹的发展过程和最大主应力分布变化过程。在单轴静态压缩条件下，碳纳米管与水泥基材料交界处发生应力集中，破坏单元最先出现，随着加载的进行，裂纹破坏加宽加大，裂纹主要方向为斜侧45°。

2）碳纳米管在复合材料中起桥联的作用，并且因为纳米充填作用，提升了材料的密实度。当发生断裂时，碳纳米管的拔出作用可对复合材料起到增韧作用。此外，选择合适的碳纳米管含量有利于提升材料的力学性能。

3）二维模型可以较好地模拟代表单元的应力-应变关系和损伤破坏过程，但是对于三维空间中碳纳米管的真实分布状态及其影响尚不知晓。未来可以拓展使用三维基面力元法，模拟研究三维材料单元的损伤破坏过程。

参考文献/References：

[1]吴中伟. 高强、特高强水泥基材料的研究与应用[J]. 混凝土与水泥制品， 1992（5）： 4-9.

WU Zhongwei. Research and application of high-strength and extra-high-strength cement-based materials[J]. China Concrete and Cement Products， 1992（5）： 4-9.

[2]MAKER J M， MARGESON J C， LUH J. Carbon nanotube/cement composites-early results and potential applications[C]// Proceedings of 3rd International Conference on Construction Materials： Performance， Innovations and Structural Implications. Vancouver： [s.n.]， 2005： 1-10.

[3]TRETTIN R，KOWALD T. Nanotubes for high-performance concrete[J]. Betinwerk Fertigteil Tech， 2005， 71（2）： 20-21.

[4]LI G Y， WANG P M， ZHAO X H. Mechanical behavior and microstructure of cement composites incorporating surface-treated multi-walled carbon nanotubes[J]. Carbon， 2005， 43（6）： 1239-1245.

[5]徐世烺， 高良麗， 晋卫军. 定向多壁碳纳米管-M140砂浆复合材料的力学性能[J]. 中国科学（E辑：技术科学）， 2009， 39（7）： 1228-1236.

[6]TAN Jingmei， WANG Aiguo， SU Wenjun. Mechanism of the modified carbon nanotubes toughening DSP cement mortar[J]. Applied Mechanics and Materials， 2015， 723： 406-409.

[7]陆富龙. 碳纳米管对水泥基材料的作用机理研究[D]. 广州：广州大学， 2019.

LU Fulong. Study on the Machanism of Carbon Nanotubes on Cement Based Materials[D]. Guangzhou： Guangzhou University， 2019.

[8]牛荻涛， 何嘉琦， 傅强， 等. 碳纳米管对水泥基材料微观结构及耐久性能的影响[J]. 硅酸盐学报， 2020， 48（5）：705-717.

NIU Ditao， HE Jiaqi， FU Qiang， et al. Effect of carbon nanotubes on microstructure and durability of cement-based materials[J]. Journal of the Chinese Ceramic Society， 2020， 48（5）： 705-717.

[9]刘巧玲， 李汉彩， 彭玉娇， 等. 多壁碳纳米管增强水泥基复合材料的纳米力学性能[J]. 复合材料学报， 2020， 37（4）：952-961.

LIU Qiaoling， LI Hancai， PENG Yujiao， et al. Nanomechanical properties of multi-wall carbon nanotubes/cementitious composites [J]. Acta Materiae Compositae Sinica， 2020， 37（4）：952-961.

[10]WAN H， DELALE F， SHEN L. Effect of CNT length and CNT-matrix interphase in carbon nanotube （CNT） reinforced composites[J]. Mechanics Research Communications， 2005， 32（5）： 481-489.

[11]姚小虎， 韩强， 辛浩. 单壁碳纳米管非线性力学行为的数值模拟[J]. 物理学报， 2008，57（1）： 335-344.

YAO Xiaohu， HAN Qiang， XIN Hao. Numerical simulation of nonlinear mechanical behaviour of single-walled carbon nanotubes[J]. Acta Physica Sinica， 2008，57（1）： 335-344.

[12]GAO Y C. A new description of the stress state at a point with applications[J]. Archive of Applied Mechanics， 2003， 73（3）： 171-183.

[13]彭一江. 基于基面力概念的新型有限元方法[D]. 北京：北京交通大学， 2006.

PENG Yijiang. The New Finite Element Method on Potential Energy Principle by Base Forces[D]. Beijing： Beijing Jiaotong University， 2006.

[14]浦继伟. 基面力元法在再生混凝土细观损伤分析中的应用[D]. 北京：北京工业大学， 2014.

PU Jiwei. The Application of Base Force Element Method in Recycled Concrete Meso Damage Analysis[D]. Beijing： Beijing University of Technology， 2014.

[15]PENG Yijiang， PU Jiwei. Micromechanical investigation on size effect of tensile strength for recycled aggregate concrete using BFEM[J]. International Journal of Mechanics and Materials in Design， 2016， 12（4）： 525-538.

[16]PENG Yijiang， WANG Yao， GUO Qing， et al. Application of base force element method to mesomechanics analysis for concrete[J]. Mathematical Problems in Engineering， 2014（5）： 1-11.

[17]孟德泉， 应黎坪， 杨欣欣. 基于界面等效模型的再生混凝土基面力元分析[J]. 河北工业科技， 2018， 35（4）： 248-254.

MENG Dequan， YING Liping， YANG Xinxin. Analysis of recycled concrete base on interface equivalent model using base force element method[J]. Hebei Journal of Industrial Science and Technology， 2018， 35（4）： 248-254.

[18]崔云璇， 应黎坪， 陈曦昀， 等. 不同应变率下再生混凝土动态力学性能分析[J]. 广西大学学报（自然科学版）， 2018， 43（4）： 1547-1553.

CUI Yunxuan， YING Liping， CHEN Xiyun， et al. Analysis of dynamic mechanical properties of recycled concrete under different strain rates[J]. Journal of Guangxi University（Natural Science Edition）， 2018， 43（4）： 1547-1553.

[19]杨欣欣， 应黎坪， 彭一江. 基于数字图像处理技术的再生混凝土数值模拟[J]. 河北工业科技， 2018， 35（5）： 329-334.

YANG Xinxin， YING Liping， PENG Yijiang. Numerical simulation of recycled concrete based on digital image processing technology[J]. Hebei Journal of Industrial Science and Technology， 2018， 35（5）： 329-334.

[20]彭一江， 金明. 基于基面力概念的新型势能原理有限元方法[J]. 北京工业大学学报， 2007， 33（7）： 687-692.

PENG Yijiang， JIN Ming. The new finite element method on potential energy principle by base forces[J]. Journal of Beijing University of Technology， 2007， 33（7）： 687-692.

[21]NI B， SINNOTT S B， MIKULSKI P T， et al. Compression of carbon nanotubes filled with C60， CH4， or Ne： Predictions from molecular dynamics simulations[J]. Physical Review Letters， 2002， 88（20）： 205505.

[22]付称心， 陈云飞， 焦继伟. 单壁碳纳米管拉伸试验的分子动力学模拟[J]. 中国科学（E辑：技术科学）， 2008， 38（3）： 411-420.

[23]徐波. 基于材料细观结构的混凝土数值模拟与性能分析[D]. 杭州：浙江大学， 2008.

XU Bo. Numerical Simulation and Performance Studies of Concrete Based on Matcrial Meso-structures[D]. Hangzhou： Zhejiang University， 2008.

[24]高良丽. 多壁碳纳米管增强M140DSP砂浆的力学性能研究[D]. 大连：大连理工大学， 2009.

GAO Liangli. Study on Mechanical Properties of Multi-walled Carbon Nanotubes Reinforcing M140DSP Motar[D]. Dalian： Dalian University of Technology， 2009.

[25]沈觀林， 胡更开. 复合材料力学[M]. 北京：清华大学出版社， 2006.