从空间经济学学会什么?(下)
[比利时]斯特弗·普罗斯特,雅克-弗朗索瓦·蒂斯(著)
(1.比利时勒芬大学,比利时 勒芬市 3000;2.比利时勒芬基督教大学,比利时 勒芬市 3000)
安虎森,丁嘉铖,周江涛,王 淞(译)
(东北师范大学 地理科学学院,长春 130024)
提要:空间经济学的目的是要解释财富和人口在国际和区域从城市到地方的空间分布中存在峰值和谷值的原因,其主要任务是验证导致经济活动空间聚集的向心力和导致区域以及城市经济活动空间分散的离心力的微观经济基础。交通运输在城市和区域两种空间尺度上都发挥着重要作用但发挥作用的方式不同,它重点研究区际货物流、区域尺度的乘客出行和城市尺度的个人通勤。
四、为什么存在城市
以上借用贸易和地理文献中的观点和概念讨论了区际不平衡问题。在这一部分中,我们将会看到城市是区域发展的引擎,同时把我们的注意力转移到城市经济学研究的一些子领域中,在这些领域中,土地和空间外部性是关键。
尽管城市规模的扩大需要大量成本同时还具有很多劣势,然而城市居民逐渐增多已成了许多国家的一大特征,这就意味着人们是用脚来进行投票的。虽然城市化和经济增长不一定密切相关,然而城市往往比边远地区和农村地区更适合于生存。城市主要的特征是在相当紧凑的空间范围内集中了高密度人口,同时也承载了大量的建筑物和各种各样的基础设施。
根据格莱泽(Glaeser,2011)的研究,城市存在的主要原因是为了方便人们之间的联系。如果人们不需要彼此间的相互接近,那么我们就无法解释在许多国家土地竞争如此激烈以至于居住成本在消费者支出中所占比例迅速上升的现象。家庭和厂商都寻求空间上的相互接近,因为他们因各种经济和社会方面的原因需要各方面的互动。尤其,新思想往往是旧思想的一种新的组合,因此把众多的人相互联系起来,对熊彼特式的创新过程而言是至关重要的。这具有类似于万有引力的性质,这些性质的强度随着区位附近地区的代理人数量的增多而增强,随着它们之间距离的增大而减小。尽管人们偏好短途旅行而不是长途旅行,但他们更偏好更大的空间而不是更小的空间。由于经济活动不能聚集在针尖上,因此厂商和家庭为争夺某区域自然延伸范围内的很有限的土地展开竞争。相对于这些小尺度范围土地而言,那些规模很大的区域所关注的是区域经济学所要研究的问题。
正如贝克曼(Beckmann,1976)的研究所示,个人在稳定和持久的环境中与他人发展互动联系的渴望,促使他们聚集在相对紧凑的空间范围内,因而他们所消耗的土地相对较少。贝克曼的研究告诉我们,空间经济学的基本权衡已经指出了城市存在的原因,即人口分布是促使人际互动的各种倾向实现均衡的结果,而这种人际互动是通过各种机制实现的,这些机制包括那些有利于提高厂商和消费者利益的外部的作用力,称之为聚集力,还包括那些与人口规模有关的各种空间摩擦和拥挤效应,称之为分散力。这些作用力之间的平衡决定了城市规模。
区域经济学关注的是内部规模收益递增与区际商品运输之间的权衡,而城市经济学关注的是厂商外部规模收益递增与劳动力通勤之间的权衡。下面我们首先将深入分析聚集经济;接着讨论城市的主要离心力,即通勤和住房成本;最后将分析交通拥堵和城市不同的交通运输政策问题。
(一)聚集经济
在大城市,消费者需要支付高昂的租金,承受长时间的通勤,还生活在污染的环境中,并面临着高犯罪率。但消费者为什么选择大城市居住?这是因为大城市的工资水平比小城镇高很多。那么,厂商为什么向他们的员工支付高工资?如果厂商在大城市不愿意承担高成本和赚取更高的收入,那么他们应该选择在土地和劳动力都要便宜的小城镇。城市工资补贴的原因是大城市的劳动生产率高于小城市,而且大城市高密度的经济活动①常常造就大城市的各种优势,所以大城市的劳动生产率更高。这些优势常常被涵盖在“聚集经济”名下,聚集经济包括货币外部性和技术外部性,还可能是产业内外部经济或产业间外部经济②。长期以来,聚集经济被看成是黑匣子,它隐藏着丰富的微观经济机制,而这些机制会带来总体水平上的收益递增。黑匣子已经打开了,进而现在对这些不同机制有了更好的了解,尽管它们的相对重要性仍然是一个尚未解决的经验性问题。
接下来我们首先区分厂商聚集经济和消费者的聚集经济。
1.厂商聚集经济的特征
聚集经济通常以不同的方式出现。因此,将与人口密度有关的各种机制分为以下3类是比较有利的:共享、匹配和学习(Duranton and Puga,2004)。它们的共同特点是,将形成收益递增的总体生产函数。
(1)共享主要是指共同利用那些有利于提高厂商劳动生产率的当地公共产品,例如共同利用新的信息和通信技术以及各种交通运输基础设施。共享也指获得大量的具有专业技能的劳动力以及那些大城市可以提供的各种厂商对厂商的服务。尽管厂商将大量的生产活动外包给那些具有大量廉价劳动力的国家,然而它们也只有在那些能够生产这种公共服务系统的地方才能享用这种专业化的服务。
(2)匹配意味着把工作机会很好地分配给劳动力和那些寻求就业的人,或分配给那些提供厂商对厂商服务的各种供应商和消费者。这种匹配对那些密集分布着不同类型劳动力和工作机会的市场相对于那些稀疏分布着的市场更重要。这一思想,最早是由赫尔斯利和斯特兰奇(Helsley and Strange,1990)在30多年前提出来的。当时他们发现大量潜在的雇主、劳动力居住在同一个大城市,因此在不改变原有居住区位的情况下劳动力可以转换工种,这使得劳动力更容易地找到就业岗位。厂商的大量聚集会削弱厂商的垄断力量,因此拥有相同技能的工人在大城市可以获得更高的工资(Manning 2010)。大的劳动力市场也扩大了劳动力找到就业的机会,使得劳动力不会轻易地改变其职业(Di Addario,2011;Bleakley and Lin,2012b)。最后,这种劳动力和就业的高水平匹配,使得大城市中的劳动力相对于小城市中的劳动力更加关注于其核心业务(Kok,2014)。
(3)在城市中,学习可能会让那些认为新的信息和通信技术消除了面对面交流的人感到惊讶。当不同的代理人拥有不同的信息时,收集这些信息就会产生知识溢出,这是对那些因接近研究中心、知识型公司和高技能工人而对所有人带来外部利益的简略的表述方式。思想在本质上是一种无形的商品,人们期望互联网在这些方面发挥重要作用。然而,观察表明,研究和创新活动是在世界范围内其空间分布最为集中的活动(Feldman and Kogler,2010)。这似乎是一种悖论,但可以肯定地说,一旦发现了新的东西,那它们就可以无成本地扩散到世界各地。当然,涉及知识创造和获取时,再次涉及邻近效应问题(Glaeser,1999;Leamer and Storper,2001)。
研发往往需要长时间的交流和讨论,在这个过程中,知识是通过反复的测试和差错逐步成熟起来的。因此,在彼此靠近的代理人之间进行广泛、反复的非正式接触有助于新思想的传播、协调和信任水平的提升。虽然网络可能是最好的图书馆,但它所提供的大量信息使得人们难以捕捉与其搜寻目标相关的信息。向其他人学习往往是最简单的方法,也可以知道发生了什么以及在何处搜索的问题。当研究人员聚集在一起时,就有可能产生巨大的创造力,因此创新在空间上是集中在一起的。例如,格林斯通、霍恩贝克和莫雷蒂(Greenstone,Hornbeck and Moretti,2010)发现,在一个地区布局一个大型的新的工厂会提高该地区其他工厂的生产率。不同研究工作都指出同一个方向,即知识溢出的空间范围往往是有限的③(Arzaghi & Henderson,2008;Belenzon & Schankerman,2013;Buzard et al.,2017)。此外,20世纪90年代的溢出效应与80年代的溢出效应一样,都是局域化的(Lychagin et al.,2016)。这样,不同于凯恩克罗斯(Cairncross,2001)的“新的思想会更快地传播”因而“贫穷国家可以立即获得那些曾经被限制在工业化国家的信息”的主张,经验证据支持的是与格莱泽(Glaeser,2011)的那种甚至在互联网时代,“思想通过走廊和街道比跨越大陆和海洋更容易传播”相一致的观点。太阳底下没有什么新鲜东西。像霍恩伯格和李(1985)这样的经济史学家,长期以来一直强调信息是城市存在的主要原因之一。这些结果也证实了输送人比输送货物更昂贵的观点。
尽管经验证据仍然较少,但知识溢出往往使得有技能的劳动力受益更多。在那些规模较大和受到较高水平教育的人较多的城市,劳动力改换工种比低技能劳动力居住较多的城市更容易。罗森塔尔和斯特兰奇(Rosenthal nd trange,2008)研究支持了这种观点,他们发现如果在5英里内增加50 000名受过大学教育的劳动力,那么受过大学教育的劳动力的工资水平提高6%至12%。贝克罗德、布鲁姆、斯特兰奇(Bacolod,Blum & Strange,2009)和库姆斯、德姆杰、李(Combs,Démurger & Li,2015)注意到,与大城市有关的城市工资补贴来源于认知技能而不是动作技能。这样,类似于内生经济增长理论,所有要素都像劳动力聚集会提高劳动力劳动生产率那样发挥重要作用(Morrtti,2004;Glaeser & Resseger,2010)。但人力资本空间聚集导致的积极影响在空间中迅速衰减。
在信息越来越密集的世界中,知识和信息的价值高于某些经济活动的价值。因此,城市是信息消费活动最佳的区位,尤其厂商在技术迅速变化和激烈的竞争环境中运作时,更是如此。专业化于高新技术产业的城市,可以吸引大量的高技能劳动力,反过来这些高技能劳动力帮助这些城市取得更大的发展。这样,可以确认在第三部分看到的结论是成立的,即空间不均衡越来越多地反映技能和人力资本的城际分布差异。劳动力空间分类的另一个方面是,那些处于衰落或停滞状态的城市被那种没有人力资本所支撑的产业绑在一起的现象。这种局面的形成与当地的低工资水平以及缺乏消费性商务活动密切相关。因此,既然人力资本的空间聚集会促进经济和技术的发展,那么人力资本空间聚集也会带来持久的区际分割(Moretti,2012)。这可能会导致不可忽视的政治和社会现象,即有可能滞后地区的居民通过民粹主义投票反对目前的局势(Colantone & Stanig,2018)。
大城市可能至少有以下3个方面的原因,使得其具有很高的生产能力。除了如本文所述的聚集经济外,大城市还大量聚集了不成比例的高生产率水平的劳动力和高效率的厂商。我们简要讨论一下劳动力分类以及它的作用,将在第五部分(一)中也进行讨论。至于选择高效率厂商的问题,库姆斯等(Combes et al.,2012)发现,如果控制好聚集经济和劳动力分类,那么在法国的大城市和小城市之间选择高效率厂商并没有显著的差异。
2.如何衡量厂商聚集经济
自斯威考斯卡斯(Sveikauskas,1975)、西科恩和霍尔(Ciccone & Hall,1996)的开创性研究以来,城市规模、就业密度和劳动生产率的研究取得了巨大进展。我们的目的不是深入分析为衡量聚集经济而提出的方法问题(Rosenthal &Strange,2004;Combes,Duranton & Gobillon,2011;Combes & Gobillon,2015),相反,我们将选择一些与其解释更为直接相关的主要困难进行讨论。
基本方程把城市c的平均工资ωc与该城市就业或人口密度denc联系起来了④:
log ωc=α+βlog denc+εc。
(1)
通过普通最小二乘(OLS)回归可以得出弹性β,其变化范围为0.03~0.09之间。因此,如果就业密度提高一倍,则可以提高劳动生产率2.1%~6.4%。但由于一些计量经济学的问题还没有真正得到解决,我们主张应谨慎对待这些结果。
首先,可以利用像在式(1)中省略解释变量那种简化形式,而这些变量的影响可以通过就业密度来刻画。例如,如果忽略了解释平均劳动力技能或当地公共产品差异的变量,则这相当于假设技能劳动力或公共产品在城市之间随机分配,并在随机项中加以考虑。但这种做法是难以置信的。一种解决办法是考虑额外的解释变量,主要考虑技能劳动力分布、产业组合体的组成和市场潜力等。在这一过程中,我们将会面临着那种把控制变量无数次地添加到回归方程中的我们很眼熟的过程。使用城市和工业固定效应以及利用个体面板数据时,使用个体固定效应,而不是要控制那些省略的不会随时间变化的变量。然而,随时间变化的变量仍然可能被忽略。
第二,在省略变量的情况下,残差与解释变量的相关性使得OLS估计有偏,但它有可能是由区位的内生选择所致。事实上,冲击往往是局部的,因此对代理人的位置产生影响,而这些代理人常被受益于积极冲击的城市所吸引,并排斥那些遭受负面冲击的城市。显然,这种重新选择区位会影响城市的经济活动水平,从而影响城市就业密度。因此,就业密度与因变量相关,进而与残差相关。换句话说,存在着反向因果关系,即一次不明显的冲击通过劳动力的流动性影响工资和密度,而不是相反。这不应使人感到惊讶,即一旦人们认识到代理人是可流动的,那么就业密度和工资之间就存在着双向关系。不管内生性偏差来自于省略变量还是来自于反向因果关系,解决这些内生性偏差的主要方法就是使用工具变量,这包括寻找与解释变量相关的变量,而不是与残差相关的变量。
第三,如果把高技能劳动力归类为大城市的劳动力,则可以解释大城市工资补贴的原因(Combes,Duranton & Gobillon,2008)。对劳动力劳动生产率的众多解释(例如无法观察到的个人特征或先前个人区位选择对当前劳动生产率的影响)已形成了相当广泛的共识,也就是在其他条件相同的情况下,劳动生产率的弹性相对于当前就业密度略低于0.03。这种弹性可以衡量较高就业密度产生的静态收益(Combes et al.,2012)。最近,德拉罗卡和普加(De la Roca & Puga,2017)也强调了个人在大城市工作时积累经验的重要性,当他们转移到小城市时,这些经验也随之带走。在这种情况下,静态估计也反映了某些动态效应的平均值。
无可争议的是,聚集经济确实存在。然而,有一些问题仍不是很清晰。例如,很难测试一些用特定聚集经济所解释的结果,例如本文讨论的问题以及无法用其他来解释的一些问题。在最近的一项综合研究中,法基奥、席尔瓦和斯特兰奇(Faggio,Silva & Strange,2017)对这些问题给出了合适的解释。他们指出上述各种影响是存在的,但同时强调,聚集经济是完全异质化现象的反映。例如,尽管获益程度不如高新技术产业,但低技术产业也从溢出效应中获益。尽管产业内和产业间外部效应都发挥作用,但它们对产业的影响程度是不相同的。厂商规模也发挥着重要的作用,当厂商规模较小时,聚集经济的影响往往显得更大。换句话说,专业化和垂直分工的厂商受益于空间接近性远大于大规模厂商,这可能与这些大厂商的原材料储备有限有关。
尽管取得了丰硕的成果,但公平地说依然存在许多问题。如果我们想为城市发展或城市重建制定更有效的政策,那么我们还需要深入了解不同规模城市聚集过程背后的驱动因素,以及历史和地理因素。在不同城市环境下,衡量不同类型聚集经济的相对重要性是空间经济学所面临的主要挑战之一(Puge,2010;Moretti,2011)。
聚集经济的存在具有重要意义。一旦建立起具有外部规模经济特性的经济活动,则厂商和劳动力将变得具有黏性。聚集过程的累积性特征使得由此产生的经济活动模式对不同类型冲击的韧性更加强大。私营代理商和地方政府对建筑物和基础设施的各种投资进一步强化了这种影响(Henderson & Venables,2009)。因此,如果在经济活动区位方面具有很大的灵活性,则聚集经济将会促使弹性-黏性空间模式的出现。
尽管上述的文献具有重要的意义,但值得要强调的是,城市经济学家很少关注所研究的产业市场结构,尽管不同行业之间存在着很大的差异。例如,研究商务活动的文献强调那种厂商共享知识的“协同竞争”的重要性,但在产品市场上的竞争是相当激烈的。这种市场结构促进了生产率水平的提升,推动了工资水平的上涨。此外,如果不完全的产品市场(垄断竞争)与完全弹性的劳动力市场相结合,那么劳动力的工资水平将是很低的,因为劳动力的边际生产率与厂商边际收益有关而与市场价格无关。
3.消费者聚集经济
城市也是享受消费、文化和休闲的地方(Glaeser,Kolko and Saiz,2001)。就像厂商一样,生活在大城市的消费者也受益于分享、匹配和学习过程,他们享用各种不同的可交易和不可交易的商品和服务、良好的交通和通信基础设施、广范围人际联系和文化设施以及社会交往机会。城市的高密度人口使得消费者可以以较低的出行成本获得各种各样的商品,因此有必要研究差异化产品的供应如何影响城市居民福利的问题。一个典型的不可交易的例子是餐饮业提供的各种饮食服务,这种饮食服务支出占家庭总支出的5%以上。库特勒(Couture,2016)利用产品差异化研究中开发出来的新的分析工具指出,消费者为享受他们所偏好的饮食,愿意承担高额的出行成本,从而证实了作为一种消费型设施的各种不同类型基础设施的重要性。众多人口也有利于获得那些在人口分散居住的情况下无法获得的地方公共产品。
大量的差异化商品给那些偏好多样化、偏好异质性商品以及收入水平不同的消费者带来巨大的利好。大城市具有巨大的异质性消费群体,寡头垄断理论认为市场竞争越激烈,越能提供种类繁多的商品和高质量的商品(Campbell and Hopenhayn,2005;Berry and Waldfogel,2010;Schiff,2015)。结果,如果其他条件都相同,那么大城市的商品市场价格应比小城市的市场价格低,这符合规模较大区域的价格指数低于规模较小区域的经济地理模型。利用条形码数据,汉德伯里和温斯顿(Handbury and Weinstein,2015)比较了同一连锁店的相同食品的价格。他们的数据包括美国49个城市33 000名消费者的数十万种商品价格。调整商品、零售商和消费者特性后他们发现,价格几乎与人口规模无关。汉德伯里和温斯顿还发现,当城市规模扩大一倍时,商品数量增加20%。当价格指数来解释获得性效应时发现,大城市的杂货价格略低于小城市的杂货价格。例如,对纽约和爱荷华州得梅因市的相同商品而言,纽约的价格要低1.3%。至于服务业,情况可能会有所不同。生产消费性服务的劳动力应该得到更高水平的工资,以补偿他们在大城市承担的高额居住成本和通勤成本。因此,服务行业的价格水平应该更高。在大城市,消费性服务业提供的服务质量高和所提供的服务种类也更多(请参见戈比伦和米尔森特(Gobillon and Milcent,2013)的法国医院案例研究)。
简而言之,除了住房成本之外,城市规模对生活成本的影响仍是一个有待解决的问题。这个问题并不是纯粹的学术问题。当居住成本包括在内时,生活费用随城市规模的扩大而增加是可以预期的。在这种情况下,联邦税或国家所得税以名义收入为基础,就意味着劳动力的城际分配是不合理的。由于劳动力流动是由实际收入差异所驱动,因此劳动力是在受到某种诱导下,从高效率、高工资的城市迁移到低效率、低工资的城市。奥尔伯伊(Albouy,2009)发现,美国劳动力从北部向南部、从人口稠密地区向人口稀疏地区的错配,就导致了美国2008年约280亿美元的福利损失。
然而,在城市效率低下的情况下,消费型基础设施会产生相反的影响,这些主要发生在发展中国家。换言之,城市化不一定意味着工业化和贸易。戈林、杰德沃德和沃尔拉特(Gollin,Jedwab and Vollrath,2016)根据116个发展中国家1960年至2010年数据发现,严重依赖自然资源的国家与消费型城市的出现是很有关系的,这些消费型城市主要生产不可交易的服务。另一方面,生产型城市主要依靠制造业的发展和可交易商品的生产,这些城市的绩效比前一种城市的绩效好很多。在前一种城市的情况下,城市化是荷兰病的征兆。
(二)通勤成本与住房成本的均衡
与城市规模有关的积极影响常伴随着各种负面影响,如昂贵的住房、长距离通勤、交通拥堵、污染和犯罪等。这些影响带来了所谓的城市成本。结果,城市可以视为聚集经济与城市成本之间均衡的结果。
1.单中心城市模型
冯·杜能研究了一个集镇周围农作物的空间分布,他是第一个提出要分析土地分配给不同经济活动的不同分配方式的人。以杜能模型为基础建立起来的权威性的城市经济学模型是一个缺乏特色的单中心城市模型,其中,由唯一的又是外生给出的中央商务区(CBD)提供所有的就业机会,因此城市内不同区位都具有异质性特征。该模型中每个区位的唯一空间特征是它与CBD之间的距离,故而这个模型也打破了第二部分(二)所强调的决策区位时的相互依赖关系。因此,该模型更加符合竞争范式。每个消费者利用单个区位上的土地,并在居住地和工作地点之间进行通勤。因此,单中心城市模型就是研究空间经济学基本均衡的城市版本,也就是主要研究某一区位上的居住面积(居住面积以该区位上使用的土地数量来近似表述)与离CBD的接近程度(接近程度用通勤成本来表述)之间的权衡⑤。
消费者并不喜欢长距离通勤,因此他们为得到尽可能靠近CBD的土地展开竞争。但消费者又偏好较大面积的空间,故消费者也不会挤进中央商务区附近,他们中的一些人愿意长距离通勤。如果向一些消费者分配给接近CBD附近的一块土地,那么间接增加了其他消费者所承担的通勤成本,因为他们被迫离得更远,故确定消费者在城市中的区位是一般均衡问题。完全竞争的土地市场可以维持相同消费者在不同区位上的分布,进而实现均衡时效用水平的均等化。该主张的推理过程很简单且不会引起怀疑,即土地使用者的行为就类似于参与了一场巨大的拍卖活动,在消费者的收入水平和偏好给定的情况下,消费者行为可以由地租竞标函数来表征,而地租竞标函数表述的是对离CBD任何距离x处的单位土地的意愿支付,特定地块就分配给出价最高的投标人。消费者的数量很大(形式上是连续的),且胜出者支付最高的出价,因此,土地租金是消费者地租竞标函数的上包络线。
设V[R(x),Y-T(x)]为间接效用。消费者是同质的消费者,故在均衡时,他们在所有区位上享有相同水平的效用。因此,V[R(x),Y-T(x)]对x的导数必等于零。利用罗伊恒等式,可以得到阿隆索-穆特均衡条件:
(2)
由于长距离通勤产生很高的通勤成本(dT/dx>0),故地租随离CBD距离的增加而降低才能维持上述平衡条件。因此,式(2)意味着与长距离出行有关的通勤成本的边际递增完全可以由居住成本的边际递减所弥补。坦率地说,人们用较便宜的土地换取较高的通勤费用。如果通勤成本与距离无关(dT/dx=0),则地租将恒定且等于土地R0的机会成本。因此,通勤成本是原因,土地租金是结果。在无特色的单中心城市模型中,能够解释城市地租超出土地机会成本的“某种东西”就是与CBD的远近有关的自然距离。此外,消费者占用的土地数量随与CBD的距离的增加而增加。虽然较长的通勤距离导致较低的净收入Y-T(x),但空间均衡条件又导致对土地的补偿需求,而这种补偿取决于土地租金和所有消费者的共同的内生性效用水平。每个消费者的影响力弱,无法影响效用水平,故效用水平看成是已知的。住房是正常商品,因此较低的土地价格意味着更高的土地消费。换句话说,随着与CBD的距离的增加,土地使用越来越多,复合商品消费逐渐下降。反过来,这又意味着人口密度随与CBD的距离的增加而逐渐减少。因此,较低的通勤成本促进了城市的分散化。
尽管相当简单,但单中心城市模型具有一些重要的启示,即当众多的消费者聚集在一起时,土地消费成为一种促使分散的力量。为了解它的运作,我们先假设消费者群体N承担城市成本C(N,u),且享受u水平的效用。城市成本C(N,u)是通勤费用、复合产品生产成本以及城市居民占用的土地的机会成本之和,该成本是消费者实现效用水平u所要支付的成本,可以写成如下:
(3)
其中,Z(h(x);u)是满足等式U[Z(h(x);u),h(x)]=u成立的复合商品数量,B为内生的城市界限,n(x)=1/h(x)为人口密度。可以证明,C(N,u)对N是严格递增且严格凸,对u也是严格递增的(Fujita and Thisse,2013)。因此,如果效用水平要保持不变,那么由居民来承担的城市的平均成本随新居民的增加而增加。换句话说,土地使用和通勤成本对人口规模而言是聚集不经济的。
地租水平不仅反映了与CBD的邻近程度,而且还反映了土地“人为的稀缺”程度,而这种土地稀缺是因土地使用限制、制定空间开放规定或那种维持农产品价格高于国际水平的公共政策所导致的。例如,实施城市规模控制措施,将导致新居民福利水平的下降或迫使一些人离开城市(Glaeser,Gyourko and Saks,2006)。此外,由于控制人口规模,这些政策也无法使得那些生产力水平很高的城市充分利用其潜在的聚集效应。要承认的是,如果从环境和美学方面考虑,则需要绿色的空间。然而,提供这种空间有关的收益,必须根据它们对人口施加的成本加以衡量。根据切希尔、内森和奥弗曼(Cheshire,Nathan and Overman,2014)的报告,“在2010年,英格兰东南部的住宅用地价格是农用地价格的430倍”。我们很想知道应配给绿色空间多少影子价格使得这种价格差异才趋近于合理。
对土地管制所产生的各种社会福利效应进行综合性经济计量分析后,特纳、霍沃特和冯德科劳沃(Turner,Haughwout & van der Klaauw,2014)得出结论说,土地利用管制的边际减少可能带来巨大的福利改进,尤其在现有发达地区的边缘地区更是如此。更令人惊讶的是,谢和莫雷蒂(Hsieh and Moretti,2019)发现,在1964年到2009年期间,对纽约、旧金山和圣何塞住房供应限制降低到中部美国城市水平,使得美国GDP增长了8.9%,这是一个天文数字。当然,要准确评估大量的土地和住房管制的社会成本,还需要做大量的工作。尽管如此,我们可以相信这一成本绝不会很小,因为土地使用限制会导致劳动力在城市间的不合理配置⑥。
因此,与许多媒体和公众的看法相反,许多城市居住成本的上升主要是因为过度管制住房和土地市场的缘故。公共政策通常对住房和办公用地的管制是相当严格的。这些政策通过实行人工的土地配给降低住房供应的价格弹性,还提高了那些与人口和就业规模同步变化的土地租金以及不平衡性。由于边际城市成本dC(N,u)/dN变大,因此这些限制政策的受益者是那些土地和建筑物的拥有者。那些年轻人和新居民是这些价格上涨和排挤效应的受害者,这些影响往往使得他们的生活条件变得更加困难,或阻碍人口的迁入(Ganong and Shoag,2017)。
从单中心城市模型中得出了许多结论,且这些结论与城市的一些主要特征是相一致的。然而,城市经济学的基本模型在预测城市社会结构方面还存在欠缺。例如,如果消费者收入不相同,则该模型得出一个相当极端的结论,即随着离CBD的距离的增加,不同收入水平的家庭是以收入递增顺序进行排序的(Hartwick,Schweizer and Varaiya,1976;Fujita,1989)。因此,如果两个家庭的收入差距越大,那么他们居住地之间距离也就越大,反之亦然。这并不是我们在许多国家观察到的现象,在这些国家的大都市区通常显示出U形或W形的收入空间分布格局(Rosenthal and Ross,2015)。例如,当住房按住房建设年限区分时,富裕的人们既被那些可以消费大面积土地的郊区所吸引,也被那些大规模重建使得新式住房密集的城市中心区位所吸引,这样就形成了U形的收入空间分布格局(Brueckner and Rosenthal,2009)。在这种情况下,使用那些独立于收入水平的通勤成本似乎限制了研究家庭的居住选择,因为有充分的证据表明,时间的机会成本随收入增加而变大(Small,2012;Koster and Koster,2015)。因此,为解释异质性消费者和差异化的城市环境,需要采用更加一般化的办法。但这种分析变得很困难,因为市场结果是通过解决一个多维匹配问题而得出的,而住房消费又依赖于收入。多维匹配问题到目前为止仍是无法解决的问题。
更加重要的是,单中心城市模型仍无法解释就业活动的地理集中。事实上,厂商通过第二个就业中心可以减轻大城市地区城市成本带来的负担(Henderson and Mitra,1996)。为了说明这一点,考虑一下居住面积不变的例子,也就是在不同区位上的居住面积都相同(h=1)。通勤成本为距离的线性函数(T(x)=tx)。如果x=0处的城市为单中心城市,且复合商品消费水平z为给定,那么通过区间[0,N]上的积分R(x)+tx=tN,可以得到如下城市成本水平:
C1(N,z)=tN2+z。
但当城市有两个就业中心分别区位于x=0和x=N处时,城市成本变成如下形式,即
C2(N,z)=tN2/2+z。
由于C2(N,z) 2.城市中心的出现 大川和藤田(Ogawa and Fujita,1980)在一篇很长时间内没有被人们注意到的开拓性的论文中讨论了这个问题,长时间没被关注可能是因为城市经济学仍然处于经济学边缘的缘故。作者使用一种类似于重力模型的简化模式来表示溢出效应,并把消费者和厂商结合到完整的一般均衡模型中,在这个模型中,商品、劳动力和土地市场是完全竞争的。溢出效应作为一种聚集力,其强度受距离衰减律的影响。然而,产业集群增加了劳动力的平均通勤距离,这又使得劳动力支付较高的地租。因此,厂商必须向劳动力支付较高的工资,作为厂商自己要支付的较高地租的一种补偿。换句话说,分散力来源于土地和劳动力市场之间的相互作用,而这些相反力量之间的平衡就导致厂商和劳动力的均衡分布。要注意的是与单中心城市模式的不同之处,即代理人之间的相互作用使得代理人给定区位的相对优势取决于其他代理商的区位,同时厂商聚集使得城市中心的土地变得更加昂贵。 厂商利用固定数量的劳动力和一单位土地生产同质商品,劳动者群体N中的每个劳动力都消耗一单位土地和最终消费品。区位于x(x∈[-b,b])处的厂商的产出水平Y仅取决于厂商分布: (4) 其中,τ为溢出效应距离衰减参数,m(y)为y(y∈[-b,b])处厂商密度。大川和藤田证明,均衡的城市结构是独特的单一中心模式还是不完全合并或分散的模式,主要取决于通勤费率t和溢出效应距离衰减参数τ。首先,如果通勤费用相对于距离衰减参数较高,也就是像在工业化前的城市中那样人们用步行方式通勤,那么均衡时商务活动和居住活动完全混合,也就是每个人都居住在他们工作的地方。在这种情况下,土地利用是非专业化的。随着通勤成本的下降,常常在厂商和劳动力混合分布的地块中形成两个就业中心,而这些就业中心常被居住区所包围。最终,当通勤成本足够低时(由于公共交通工具和汽车的使用),城市结构为单一中心模式。我们总结如下: 城市结构。假设溢出效应遵循线性的距离衰减率以及通勤成本为距离的线性函数,则存在一个常数K:(1)如果满足t<τK/2,则城市结构为单一中心结构;(2)如果满足τK/2≤t≤τK,则城市结构为不完全一体化的结构;(3)如果满足τK 我们根据溢出效应的距离衰减参数重写这些不等式,则当τ大于2t/K时,即溢出效应局限于当地的时候,就会出现单中心城市。在式(4)的情况下,大原(O’Hara,1977)也展示了如何通过在模型中增加建筑部门来解释CBD中摩天大楼的存在问题。均衡时,建筑物高度随离CBD中心距离的增大而下降。 虽然已知该主题很重要,然而很惊讶的是只有少数几篇论文探讨了较为一般化的框架或替代框架。这些缺失使得我们难以采取结构性方法来研究知识溢出问题。藤田和大川(Fujita and Ogawa,1982)考虑了一个负指数衰减函数,并通过模拟证明了多中心结构的存在。这些作者遇到的主要困难之一是均衡的多重性问题。卢卡斯和罗西-汉斯伯格(Lucas and Rossi-Hansberg,2002)利用了新古典生产函数,其中土地和劳动力是两种投入,厂商和劳动力都利用土地。除了一般的存在性定理外,他们的模拟结果与藤田和大川(1982)的结果是一致的。 伯利安特、彭和王(Berliant,Peng and Wang,2002),用受距离衰减影响的类卢卡斯外部性来替代本地厂商密度。更确切地说,厂商将根据柯布-道格拉斯生产函数进行生产: Y(x)=A(x)KαLβ。 在城市,抱怨交通条件与谈论天气一样是很普遍的现象。交通不适主要在于出行过程中因各种负的外部性而导致的各种额外成本。城市内出行时的额外成本主要来自于因当地空气污染、交通事故或气候条件所导致的交通拥堵(Parry,Walls and Harrington,2007)。气候和空气污染的影响并不仅限于交通或城市生活环境。这些外部性能够通过使用清洁燃料、催化式排气净化器、排放安全的汽车以及科学设计的房屋等降低单位活动排放量的方式有效解决。不考虑犯罪,那么城市最重要的负的外部性就是交通拥堵。美国和欧盟至今都没有有效解决在其定价政策和基础设施建设方面的负的外部性,这些是阻碍这些国家的城市健康发展的主要因素。如何解决城市密集而产生的负的外部性以及充分利用聚集经济,将是城市和交通运输经济学面临的主要挑战之一。 人们在城市内出行有很多方面的原因,比如通勤上班、商务联系、接送孩子、在市中心或郊区商场购物以及参加各种家庭和社交活动等。城市经济学主要关注聚集经济与工作地点可达性之间的一种均衡问题。按照这种均衡,城市规模和结构在很大程度上取决于其交通运输系统的状况。为了评估各种政策可能产生的影响,区分两种根本不同的手段是相当重要的,也就是要区分好通过定价和监管更好地利用现有运输基础设施的政策和增加运输能力的政策。 1.通过收费缓解交通拥堵 自从庇古(Pigou,1932)的开创性工作以来,经济学家之间已形成了一种共识(但不是普遍),即道路收费是解决交通拥塞的理想手段。这种观点是很直接的,即如果汽车数量超出特定密度,则出行速度随汽车数量的增加而下降。虽然出行延误所造成的成本由司机承担,然而每个司机都忽略了他们造成其他人出行延误所带来的外部成本,其结果是出行时间的增加和无效率的低速度。因此,提高效率可以诉诸征收相当于边际外部成本的费用。 根据静态峰值负荷定价理论,可以解释如下。考虑两个区位A和B由一条道路相连接。当交通没有拥挤时,出行成本是恒定的,且标准化为零。居住在区位A的N个同质性用户希望同时前往区位B,但道路的通行能力不足以满足这种要求。最简单的情况是,道路上有一个单位时间内只能通过s辆汽车的瓶颈。在这种情况下,(平均)出行成本由ATC(N)=αN/s给出,其中α为出行时间的影子价格。由于总出行成本为TTC(N)=αN2/s,故出行的边际社会成本是MTC(N)=2αN/s,边际外部成本是αN/s。如果每个用户支付αN/s的通行成本,则用户把外部成本内部化了。此外,如果出行的反向需求曲线为D(N),则最佳出行次数由D(N)=2αN/s给出。相比之下,在没有收费的情况下,均衡时的出行次数是由等式D(N)=αN/s给出。因此,传统的峰值负荷定价模型要求在边际社会成本定价情况下,必须减少出行次数。这样,在通过就业活动空间聚集提高城市劳动生产率和降低交通拥堵之间产生了潜在的冲突。 庇古提出的解决方案是静态的。然而,道路拥堵本质上是一种动态的现象,因为出行者不必在同一个时间出行(Vickrey,1969)。现考虑一下由阿诺特、德帕尔马和林赛(Arnott,de Palma and Lindsey,1993)建立的瓶颈模型。开车司机都有在理想的时间内到达目的地的想法,如果他们提前或延迟到达,则会带来计划日程延误费用。设β(β<α)表示早到的单位成本,γ(γ>α)表示晚到的单位成本,如果车辆到达瓶颈路段开始处的数量超过s,则会形成排队,出行总费用是排队延误费用、日程延误费用和通行费用(如果有的话)的总和。设τ(T)表示在时刻T征收的通行费,N(T)表示在时刻T排队的车辆数量,则在时刻T通过瓶颈路口的驾驶员的出行费用为C(T)=αN(T)/s+β(早到时间)+γ(晚到时间)+τ(T)。 由于司机是同质的,因此在每个司机出行期间的均衡出行成本是相同的。如果没有通行费,则排队时间从出行过程开始时的零增加到个体准时到达目的地的时间的最大值,然后在出行过程结束时减少到零。阿诺特和合作者的研究表明,均衡出行成本为δN/s,其中δ≡βγ/(β+γ)。排队时间是无谓的损失,因此均衡是无效率的。排队可以通过征收随时间发生变化的通行费来避免,这种通行费从零开始起步,以β费率线性提高到个人按时到达目的地所需时间最大时的通行费为止,然后以γ费率线性减小到零。在这种情况下,消除了排队成本,然而计划日程延迟成本不变,因为瓶颈路段仍然以最大容量通行且司机到达的时间间隔不变。此时,出行的社会成本从δN/s下降到δN/2s,但包含通行费的私人成本与不收通行费时的私人成本相同,故均衡的出行次数仍由D(N)=αN/s给出。因此,根据随时间变化的通行费,在没有减少出行次数的情况下,出行的社会变量总成本下降了一半。换句话说,与密度相关的益处并没有受到太大的影响(Arnott,2007),但是由于在庇古静态模型中的计划日程延误成本没有变,故不会消除拥堵成本。 到目前为止,我们假设汽车用户重视时间的程度是一样的,然而经验证据表明,个人的出行时间价值并不相同(Small,Winston and Yan 2005)。在这种情况下,如果以高价值出行(商务旅行和高技能通勤者)替代低价值出行,那么道路收费会产生额外的好处。道路收费减少高峰期出行者数量,使得商务对商务的出行更加方便,进而有利于提高劳动生产率。此外,个人在计划日程延迟方面的偏好也不相同(Koster and Koster,2015)。以时间价值异质性和计划日程延迟异质性特征相结合为基础,范登堡和维尔霍弗(van den Berg and Verhoef,2011)揭示了在通行费收入被重新分配之前,如何通过征收随时间变化的瓶颈路段通行费方式,充分利用好偏好的异质性以便实现帕累托改进的问题。上述议题是相当重要的,因为越来越多的证据表明,长距离通勤者容易缺勤,常常迟到,缺乏工作的积极性(van Ommeren and Gutiérrez-i-Puigarnau,2011)。 尽管存在这些告诫,但我们可以得出结论说,瓶颈路段的智能化定价可以把排队等候状况转变为通行费收入,带来时间的节约和生产率水平的提升,这对新的昂贵的交通基础设施建设而言是一种明智的选择,这也可以抑制经济活动的空间蔓延。 2.拥堵收费的艰辛之路 交通运输经济学对拥堵收费已经进行了深入的研究。在经济代理人具有固定生产区位的情况下,我们已较好地把握住了一些成问题的议题,然而文献很少涉及拥堵收费的区位效应问题。我们可以总结出3个方面的认识。首先,道路收费计划的设计对总体净福利的影响非常大(Anas and Lindsey,2011)。例如,斯德哥尔摩实施的计划比伦敦实施的计划更有效。斯德哥尔摩收费系统的交易成本较低,且根据一天中的不同时段实施更加差异化的收费标准。的确,正如瓶颈路段模型所示的那样,区分时段差异对于获取全部拥堵收费收益是至关重要的。像伦敦那种简单地划分为昼夜两个时段,那么基本上放弃了拥堵收费中的大部分收益,且主要依靠减少高峰期汽车出行总数来缓解交通拥堵。其次,对于消除大多数排队状况所需的降低10%~20%汽车使用量中,只有较小部分的(低于40%)汽车出行被公共交通所取代,而其余部分由共享汽车、组合出行或放弃出行等所取代了(Eliassonet et al.,2009)。 第三也是最后,标准的成本效益分析(CBA)只限于分析交通运输部门内部的影响,然而城市经济学认为,高密度交通线路带来巨大的交通便利性,而这种便利性带来更广泛的经济收益。安德斯蒂格等(Anderstig et al.,2016)估算了斯德哥尔摩的交通可达性与劳动力收入水平之间的关系。他们发现,总收入增加与节省时间带来直接收益是同样重要的。因此,标准的成本效益法分析拥堵收费只关注节省时间所带来的直接收益,这可能大大低估了提升交通可达性所带来的总收益。金本(Kanemoto,2013)通过建立空间与运输经济学之间的联系,重新探讨了成本效益分析的基本框架。那些降低城市通勤成本的交通运输项目,可以吸引其他城市的劳动力,这样该城市所增加的聚集收益可能以其他城市的聚集收益损失为代价。在这种情况下,如果其他城市的聚集经济效应更大,则该城市总体收益为负。相比之下,如果该项目影响了不完全竞争市场中生产的商品的运输成本,那么额外的收益始终是正的,且与厂商的定价成正比。因此,当我们要衡量更广泛的利益时,需要更加谨慎。 在美国,关于道路是否收费的问题似乎在公开辩论中是被禁止的,人们关注的更多是收费道路类型的选择问题,比如收费车道等。付费车道常把驾车者引向不收费的其他车道上,因此只有当汽车使用者的时间价值不同或对瓶颈路段通行费进行微调时,付费车道才有可能产生净福利收益(Small & Yan,2001)。霍尔(Hall,2018)考察了瓶颈路段处的拥堵随着排队而加重的现象。霍尔的研究表明,对车道收费即使在收入重新分配之前也可以产生帕累托改进。的确,如果有足够多的高收入驾驶者使用付费车道,则可以缓解免费车道上的拥堵。在欧盟,只有少数几个城市(伦敦、斯德哥尔摩、米兰和哥德堡)实施拥堵收费方案,大多数国家和地方政府基本上都赞成其他的政策,例如高汽油价格、对基础设施的大量投资以及公共交通补贴等。 有人可能不能理解,虽然潜在收益这么高,但为什么道路收费却如此不能流行?德德博杰和普罗斯特(De Borger and Proost,2012)对此提出了政治经济学的解释。人口先验地分为3类:不开车的人、易于转换成为坐公交车的驾驶员(称为边际驾驶员)以及转换成本很高的驾驶员。如果通行费收入在所有人之间平均分配,那么不开车的人将支持拥堵收费。因此,不开车的人和边际驾驶员成了支持拥堵收费的主体。如果所有驾驶员知道的转换成本只是改换为坐公交车的平均转换成本,那么边际驾驶员预期所要承担的转换成本可能比实际的成本还要高,因此,大多数人有可能反对拥堵收费。但如果实施道路收费,则可以解决不确定性,结果边际驾驶员知道他们的转换成本低于预期,因此事后可能会支持拥堵收费。因此,大多数驾驶员可能事前反对道路收费,甚至反对实验,因为他们认为自己的预期收益为负数,但大多数人在实施后可能会支持道路收费。据伦敦和斯德哥尔摩的案例,实施前大多数人反对道路收费,但实施后大多数人支持道路收费。最终决定取决于地方政府组织此类实验的能力。 传统观点认为,拥堵收费提高通勤成本,因此拥堵收费将导致城市更加拥挤。但最近的几篇论文,在假设代理人根据出行成本的变化而改变出行地点的情况下,对拥堵收费的价值提出了不同的看法。高山和桑原(Takayama & Kuwahara,2017)根据上面的瓶颈路段模型指出,如果通勤者为异质性通勤者,那么城市不会发生更加拥挤,相反,根据通勤者偏好的这种分类可能导致均衡时城市拥挤程度较低。布林克曼(Brinkman,2016)根据俄亥俄州哥伦布市的数据校准了包括拥挤成本和聚集经济的空间一般均衡模型。拥堵收费可能会产生负面影响,因为拥堵赋税虽然可以有效降低拥堵程度,但通过分散就业会减弱聚集效应。尽管从部分论文中得出确定的结论似乎为时尚早,但似乎拥堵收费具有各种意想不到的影响,需要更加认真地调查研究。这些论文还强调了统计调查的一个主要目的,即在固定区位或可变区位情况下,参数的变动可能导致截然不同的结果。 3.运输基础设施扩充可以解决拥堵问题吗 建立新的道路基础设施可能提高道路通过能力s的值,并对于任何给定的N,降低了平均出行成本AC(N)。但这种主张忽略了以下事实:扩大道路通过能力时,交通量不会保持不变;新的通行能力吸引了更多的汽车使用者(N变大)。最终,扩大道路通过能力可能会产生自身需求,这种现象被称为唐斯悖论(Arnott & Small,1994)。这种悖论所反映的无非就是对那些随出行成本的变化而变化的交通运输的需求。但这一悖论不仅仅是一种求知欲吧?当杜兰顿和特纳(Duranton and Turner,2011)重新讨论1983年、1993年和2003年美国城市问题时,特别注意到了道路通过能力与交通密度之间的同时性问题。他们的结论,对以交通基础设施建设为基础的拥堵解决政策的有效性提出了质疑。首先,杜兰顿和特纳的研究证实了新的道路建设会产生更多的交通运输的结论。更重要的是,在没有道路收费的情况下,他们发现“新的道路通行能力建设导致与其同比例增长的汽车数量”。换句话说,道路使用对城市车道总长度的弹性接近于1,这样具有了有关唐斯悖论的结论。但增加的出行者从何而来?杜兰顿和特纳发现,新的轿车和卡车几乎同等比例地扩大了交通出行量。此外,道路扩建吸引了大量的公共交通乘客。这又降低了公共交通出行频率,从而增加了等待时间和日常计划延误的成本,这种恶性循环可能导致公共交通替代工具的消失(Arnott and Small,1994)。最终,道路将吸引更多的用户。在美国,这种现象并不罕见,因为美国的汽车使用成本较低,且公交替代工具很少。苏和张(Hsu and Zhang,2014)发现,在日本,道路使用对道路通过能力的弹性相对较高。 就像降低运输成本会影响厂商区位一样,大幅降低通勤成本的大型交通项目可能会影响家庭居住区位的选择。例如,鲍姆-斯诺(Baum-Snow,2007)发现,在1950—1990年期间,穿越中心城市的新建公路将其人口减少了大约18%。他的估计表明,如果不建州际公路系统,那么中心城市总人口大约增长8%。在1960年,中心城市仍然是66%的通勤者的出发地或目的地,但这一比例在2000年已经下降到38%了。这表明工作岗位也已跟随其居民郊区化了。但需要注意的是,好几种力发生作用(Brueckner,2000)。同样,加西亚-洛佩斯、霍尔和维拉德坎斯-马萨尔(Garcia-López,Holl and Viladecans-Marsal,2015)研究了公路建设对西班牙城市化模式的影响。他们发现,在1960年至2011年之间,以中心城市为起点的公路,使中心城市人口减少了8%~9%。此外,公路促使那些有出口匝道的郊区自治市的人口增长20%。最终,每靠近公路出口匝道一千米,提高城市人口密度8%。所有这些都证实了公路通行能力的提高对大都市区人口分布有很大的影响。 上述结果在两个方面与许多政策性建议相矛盾:如果不实施道路收费,则修建新道路可能不是减少交通拥堵的合适的政策;此外,新的道路可能会对城市形态产生意想不到的不利影响,故作为遏制城市交通拥堵的主要政策性工具,交通拥堵收费已成了政策舞台上的主角。尽管决策者对此类工具缺乏热情,但城市交通经济学所获得的大量成果仍鼓励各国政府以比照新的交通项目的长处为基础,认真评估精制收费方案的优缺点。 考虑到运输基础设施的长期影响及其可能产生的外部性,城市运输基础设施需要进行规划。经济学家以标准成本效益分析技术为基础,评估运输项目的可取性。在过去的50年中,标准成本效益分析技术得到了快速发展,已经从杜普伊消费者剩余计算方法发展到纠正外部性、市场缺陷和计算更广泛的经济收益以及公共资金机会成本的方法。然而,标准成本效益分析方法在正确评估这些影响方面仍面临很大的障碍(Redding and Turner,2015)。这就需要建立更普遍化的运营操作模型,把土地使用和运输基础设施(LUTI)与那些经济地理学理论模型所强调的区位间的一般均衡相互作用结合起来。与大多数标准成本效益分析方法不同,LUTI模型是其城市空间由有限区位组合所组成的一般均衡框架。每个区位上的土地都可以用来进行生产和居住,且不同区位是通过交通基础设施相互连接起来的。LUTI模型也考虑聚集经济因素。 有两种类型的模型。一是修改了的模型,在该模型中,收集有关当前均衡的信息,并利用从文献中获得的各种弹性信息来进一步补充,使得该模型更加符合当前观察到的现象。阿纳斯和刘(Anas and Liu,2007)对这种模型进行了详细说明,这可以看作是在第五部分(二)中讨论的空间计量模型的一种解释。第二种模型的很好的例子是托伊林斯、奥萨吉纳和德格鲁特(Teulings,Ossokina and deGroot,2018)的研究,他们利用详细的微观数据,建立了包括荷兰3 000个邮政编码的空间一般均衡模型。该模型允许人口密度、就业区位发生变化,也可以选择不同的经济模式,而这种经济模式具有异质性劳动力和多种运输方式。在评估阿姆斯特丹地区新隧道的影响时,托伊林斯和合作者发现新隧道建设所产生的福利收益主要来自于出行时间的节省,土地用途变更的福利收益大约占总福利收益的30%。 4.大公交可以实现什么 实施城市公交低价政策,通常是作为弥补道路拥堵收费损失的次优收费工具提出的。实际上,便宜的公交票价不能解决道路拥堵问题,它们反而创造了大公交系统拥堵这一新的交通拥堵。如果低廉的公交价格能够解决道路拥堵问题,那么公共交通应成为使用汽车的替代品(Parry and Small,2009)。在式(5)中,最优公交票价应等于其社会边际成本,并以价格与汽车使用的社会边际成本之间的差距进行校正。由于在没有拥堵收费的情况下,高峰期时增加的汽车的成本低于其社会边际成本(Pcar PPT=SMCPT+φ(Pcar-SMCcar)。 (5) 帕里和斯莫尔(Parry and Small,2009)发现,当φ=0.5时,补贴接近城市轨道交通平均运营成本的90%是会得到社会认可的。但是,经验研究发现φ的值通常小于0.5。例如,如果φ=0.2,则峰值时段的最佳补贴从90%下降到10%。 因为强有力的交通密度经济,铁路和地铁系统显示出规模收益递增特征。因此,最优收费会导致巨额赤字,这就需要那种考虑公共资金的机会成本并为弹性较小的用户提供额外收益的拉姆齐-博伊蒂厄克斯定价方案,以进一步减少公共交通系统的赤字。公交系统的规模经济强度较弱以至精准的峰值负载收费也有可能造成公交车系统失灵,而且,除非公交车有单独的车道,否则公交车也会造成道路拥堵。因此,需要更有效的公交车收费系统,这些系统应考虑高峰期出行和非高峰期出行之间的成本差异,并随出行区域和出行距离以及道路拥堵程度而变化。这将提高城市交通系统的整体效率,并减轻城市公共交通机构的财务问题。 道路和公共交通的组合是在拥有各种不同类型用户的城市中做出政治选择的结果,但布吕克纳和塞洛德(Brueckner and Selod,2006)的研究表明,平等的投票制不一定能产生最佳的功能组合。 现在应该很清楚,我们需要更好地整合在上述两节中讨论的不同类型的空间摩擦,以了解作用在不同空间尺度上的力量是如何影响经济的。世界大多数国家的国内贸易规模远大于国家间贸易,大城市又是这种交易过程中的主要参与者。因此,最主要的是要把握城市规模和结构是如何影响区际和国际贸易,以及反过来,贸易和市场一体化是如何影响城市结构的问题。同时,这些应在多区域框架下进行讨论,因为多区域框架可以刻画出尽可能多的一般均衡效应。接下来,我们讨论两种不同的研究路径。首先,要讨论城市系统的形成,因为区域经济状况往往由它们所包括的城市的经济状况所决定。其次,要讨论建立空间计量模型的策略问题。乍一看,这两种路径似乎没有共同点,在分析方法上也有很大区别,但每种路径都可以看作是包容区域和城市经济学众多不同组成要素的尝试。这些各种“新”“旧”要素的不同组合,会给我们提供新的和可供选择的研究路径。 空间经济学中长久不衰的研究议题可能是涉及大中型城市、城镇和村庄的城市体系的问题,这些体系生产和交易不同的商品并容纳各种类型的劳动者。两代模型刻画了这类问题的不同方面。第一代模型关注城市规模和专业化,第二代模型关注城市的技能组成。 1.城市在规模和专业化上的区别 尽管克里斯泰勒(Christaller,1933)和廖什(Lösch,1940)在早期的城市研究阶段做出了巨大的贡献,但仍可以说亨德森(Henderson,1974,1988)是第一个开发出引人注目的最初的城市研究方法的人,这种方法可以描述城市体系的形成过程。他的研究框架涉及大量的从事商品交易的专业化城市。在他的研究框架中,城市体系类似于各种各样的小型开放经济体,在这些经济体中,厂商在完全竞争和外部规模经济条件下从事生产活动,城市市场以土地开发商之间的竞争为主要特征。土地开发商知道,如果以当地土地租金最大化的方式组织城市,又把属于不同工业部门的厂商聚集所产生的外部效应内部化,则可以从中获益。均衡时,各个城市的效用水平相同,每个城市的规模有效率是有限的。如果城市专业化部门不同,那么城市规模也不同,因为不同产业形成不同的外部经济。 藤田和蒂斯(Fujita and Thisse,2013)的研究表明,均衡将涉及如下公式,即 (6) i类城市规模由式(7)给出,即 (7) 其中,k≡(4γ1/t)γ1/(1-γ1)(1-γ1),k随t变大而变小。由于大城市的成本高于小城市,因此大城市的工资水平高于小城市。这反映出一个事实,即大城市的回报率更高。 因此,均衡时i类城市的数量随规模经济强度的提升而减少,随通勤成本的下降而增加;均衡时的城市规模随收益递增强度的提升而变大,随通勤成本的上升而变小。如果对商品i的支出份额很大,则将会存在大量的i类城市,但它们的规模保持不变。根据式(6)和式(7),收益递增和通勤成本之间的基本均衡按如下方式塑造城市体系。(1)如果生产商品i时的规模收益递增强度越大,则i类城市的数量越少,但它们的规模就越大;(2)如果通勤成本上升,则所有城市的规模都变小,但每种类型城市的数量增加。规模收益递增避免了城市数量的剧增(当γi→0时,mi→),而通勤成本的上升避免了城市规模的无限大(当t→0时,)。 一般认为,大公司为像公司总部和生产厂家之间的这种不同职能的组合体。杜兰顿和普加(Duranton and Puga,2005)以这种共识为基础,在城市研究领域取得了新的进展。随着新信息和通信技术的发展,目前厂商能够在地理上相互分割的不同区位上配置不同的功能以便从不同区位属性中获益,但仍需要谨慎行事。生产不仅需要具体知识也需要缄默知识,因此通过电子设备进行的信息传输仍然不完整且不完善(Leamer and Storper,2001)。如果空间上分散区位的总部与工厂间的通信成本很高,那么公司将会整合所有的功能,此时城市系统将显示出类似于在上面讨论的模式。相反,如果通信成本足够低,则杜兰顿和普加的研究表明,总部区位于几个大城市,在那里它们可以享用各种类型的厂商对厂商的服务,而工厂则区位于专业化的小城市。换句话说,城市从部门专业化转向功能专业化。 藤田、克鲁格曼和森(Fujita,Krugman and Mori,1999)提出了很不相同的以经济地理学为基础的研究思路。他们假设,在规模收益递增和垄断竞争条件下,生产一些可交易的商品。农民利用土地生产农产品,但厂商和制造业部门劳动力都不使用土地。在不变替代弹性偏好下,每种商品都具有特定的替代弹性。城际贸易需要支付贸易成本,而不同商品的单位运输成本都相同。藤田、克鲁格曼和森(1999)的研究表明,随着总人口规模的扩大,将出现具有等级体系的城市系统,高等级的城市提供大量的制造业产品。因此,出现了城市多样化趋势。此外,不同城市生产差异化的产品,因此城际贸易是双向的贸易。这样,城市间的水平关系被叠加在城市系统的金字塔结构上。城市和那些农民居住和工作的农村地区之间也存在贸易,但城市并没有空间上的扩展。故该方法仍属于CP模型传统体系中的方法。 德斯米特和罗西-汉斯伯格(Desmet,Rossi-Hansberg,2013)构建了另一种模型,该模型在不诉诸专业化和贸易情况下也可以解释城市体系的形成。人口是由具有相同偏好且完全流动的个体所组成。城市规模分布是生产效率、消费便利设施和空间摩擦3个影响因素相互作用的结果。便利设施是影响偏好的外部因素,主要的摩擦来自单中心城市中的通勤。通勤需要由劳动力税赋资助建设的公共基础设施。该模型对居民人数超过5万人以上的美国城市进行了校准,并利用校准后的模型评估了上述3个影响要素对城市规模分布和公用事业水平的影响。如果消除效率、便利性或摩擦方面的差异,那么将会导致人口在城市之间的重新分配,但这种重新配置所带来的福利提升效应较弱(最多2%)。这意味着劳动力的完全流动性,在“重新优化”城市分布和控制福利损失方面发挥重要的作用。他们对212个中国城市也进行了同样类型的试验,其结果表明这些使得中国城市规模分布发生很大的变化,同时也带来了巨大的福利改进,在某些情况下福利改进超过了40%。对这种差异的一种可能的解释是,中国国内的劳动力转移受到了很大限制,这阻止了中国大城市达到其有效规模(Au and Henderson,2006;Bosker et al.,2012)。这种建模方法有助于人们了解空间经济学中的主要驱动力是如何通过相互作用确定城市分布的问题。但模型过于格式化,以至无法追踪研究劳动生产率差异和便利设施差异的来源问题。 齐普定律是城市数量和人口规模所遵循的很简单但很有用的经验法则,它引起了人们的很大关注。1913年,德国地理学家费利克斯·奥尔巴赫(Felix Auerbach)发现了该经验规律:对于给定国家,城市人口规模及其在规模分布中的等级排名的乘积,大致是恒定的。换句话说,假设有一个最大的1型城市,则两个2型城市各自的人口规模相当于最大城市人口P1的一半,3个3型城市则各自的人口规模为该最大城市人口规模的1/3,依此类推。用Pi来表示在城市等级结构中第i个等级城市的人口,则齐普法则可以写成: log i=log P1-b·log Pi。 其中,b=1,也就是b的最大估计值接近1。如果幂函数能够提供人口分布的最好的近似值,那么b = 1是否为最佳估计值?当利用一种算法并以一致的方式确定那种具有高分辨率地理数据的城市边界时,罗森菲尔德等(Rozenfeld et al.,2011)发现,齐普法则所提供的城市人口分布与英国和美国实际城市人口分布状况是非常接近的。他们还发现,同样的规则适用于区域分布。尼奇(Nitsch,2005)在元分析中汇总了29个研究中的515个估计值,他所得出的系数b的汇总估计值接近1.1。利用城市经济学模型会得出如此惊人的结果吗? 至今,许多研究为解释齐普定律做出了相当大的努力(请参见加贝克斯(Gabaix,1999);伊克豪特(Eeckhout,2004);苏(Hsu,2012);贝伦斯、杜兰顿和罗伯特-尼库德(Behrens,Duranton and Robert-Nicoud,2014)等的论文)。现有大量的研究框架依赖于相当复杂的且有时是专门设计的模型,但这些模型最多只能提供齐普法则的一种近似值。这就是认为它是一个谜,且它持续到现在的最有可能的原因。 2.异质性劳动力与城市 在类似于亨德森模型的一些模型中,在城市里居住的是相同的且同质的劳动力。然而,有据可查的是城市里大量居住异质的劳动力,他们各自的社会组成是大不相同的。尤其,大城市的工资分布随时影响小城市的工资状况。因此,我们要研究劳动力在技能上存在差异时大城市和小城市的情形,这正是新一代模型通过研究城际和城内异质性劳动力的分类来解释的问题。重要的是,这些新一代模型可以详尽地分析人力资本问题,在第四部分(一)中已经强调了研究人力资本的重要性。均衡时,尽管所有市场已出清,但个人不会改变其区位和就业。不同于亨德森(1974,1988)的模型,这些模型不依赖于类似于开发商的“大型代理人”。换句话说,城市是因大量的小型代理人选择之间的相互作用而出现的。 (1)聚集、分类和选择经济由连续的单中心城市和具有不同的技能水平s(s∈+)的个体连续体所组成。个体的劳动生产率取决于两个因素,劳动力技能和该劳动力与某一城市的匹配程度。每个人都知道自己的技能水平,但是他和这个城市的匹配程度c是不可观察到的。当某个人位于某一城市时,他会观察自己的劳动生产率,该劳动生产率可以由φ=c×s给出,其中c(c∈+)为实现就业的随机变量,该变量可以解释那种能够确定该劳动力与城市之间匹配质量的环境因素。根据自己对自己生产率水平的了解,个体将选择成为一名企业家或工人。个人是风险中性的,他消费最终消费品和固定数量的土地,且最大限度地消费最终消费品以最大化其效用,这种最终消费品是利用CES偏好下的差异化投入品组合生产出来的,其中σ(σ>1)为不同投入品之间的替代弹性。企业家成立了一家厂商,该厂商使用劳动力生产一种产品。中间投入品生产厂商是异质性厂商,它们在垄断竞争条件下进行竞争,它们的数量等于企业家的数量。通勤成本为距CBD的距离的线性函数(tx),人均城市成本为tL/4,其中L为城市规模。 上述贝伦斯和他的合作者开发的模型的优点:(1)它可以把来自于城市规模、劳动力分类以及有效率的厂商选择的聚集经济分割开来;(2)它可以研究这些作用力如何相互作用以塑造城市系统的问题。很自然,在人口L和劳动生产率分布F(φ)已知的情况下,先从城市c开始。 人是异质的,因此存在一个临界值φmin,如果个人的劳动生产率水平φ>φmin,则该个人选择成为企业家,而劳动生产率小于φmin,则选择成为工人。生产函数为CES型函数,故企业家所占份额与人口规模L无关,这为库姆斯等(Combes et al.,2012)发现的不存在选择效应现象提供了依据。贝伦斯和他的合作者在研究法国城市时提出,可根据劳动力劳动生产率水平改写最终产品生产部门的生产函数: (8) 因此,与同质性个体中的情形一样,人均总产出与L1/(σ-1)成正比(参见藤田和蒂斯(Fujita and Thisse,2013,chap.4)的《聚集经济学》一书)。提高人口规模L,则会出现更多的生产中间投入品的厂商,这使得最终消费品生产部门更有效率,进而导致厂商支付较高水平的工资。因此,就存在与人口规模有关的聚集经济。如果城市成本扩大速度快于人均收入增长速度,也就是σ>2,则该城市的规模将是有限的。现假设每个个体的劳动生产率由λφ给出(其中λ>1)而不是由φ给出。从式(8)中可以看出,如果要素等于λ2(>1),则人均收入水平Y/L增长。然而,临界值随劳动力技能分布而变化,如果现在的劳动力技能分布为F(λφ),则新的临界值为λφmin。因此,中间投入品生产部门将拥有更多的富有效率的厂商,这些厂商支付较高水平的工资,进而企业家的收入水平也较高。换句话说,高技能的人口产生人力资本外部性,个人生产率水平也随周边人的生产率水平的提高而提升。贝伦斯和他的合作者的研究展示了这些外部性之间的相互作用如何发挥以促使劳动力技能与人口规模之间相互补充的问题,也就是说,劳动力和企业家的收入随个人技能的提高和城市规模的扩大而增加。这与德拉罗卡(De la Roca,2017)的观点相一致,他观察到移居大城市的西班牙移民是由其接受过的教育水平以及个人劳动生产率水平所被分流的。 高技能劳动力因居住和工作在成本较大的大城市而获益,而这些城市的潜在数量还很大,此时存在着唯一的一种均衡,且均衡时城市间的技能水平是相同的,但因劳动力匹配程度c的差异,城市承载着各种不同劳动生产率水平的人,包括异质的劳动力和企业家。均衡的城市体系表现出以下主要特征:城市规模随聚集经济强度(1/(σ-1))和居民技能水平(s)的提高而变大,随城市成本(t)的增加而变小。因此,应通过那些放大聚集经济的技能效应,进一步提升空间经济学基本的权衡水平。由于具有相同技术水平的两个城市的规模相同,因此可以从城市技能水平分布中查找出城市数量。如果技能的累积分布呈凹形,那么大城市数量将很少。在这种情况下,城市系统显示出金字塔形结构,效率最高的城市位于顶部,效率最低的城市位于底部。 毫无疑问,贝伦斯和合作者的研究对城市体系做出了详尽的描述,即不同城市的功能不相同,不同城市承载了大量的具有不同劳动生产率水平的人。他们的研究与其他研究不同的是,该模型确定了劳动力技能和人口规模相互补充的条件。根据亨德森(Henderson,1974,1988)的研究,大城市总体的劳动生产率水平远大于小城市的生产率水平,同时前者的名义工资高于后者,这使人感到很欣慰。两种研究框架都为解释城市工资补贴的存在提供了依据。然而与亨德森的研究不同的是,由于各个城市的生产功能相同,城市生产的最终消费品相同。这意味着城市系统是通过自给自足的过程而形成的。 (2)城市规模和学习能力据我们所知,戴维斯和丁格尔(Davis and Dingel,2019)的研究是第一篇关于各种异质性个体之间的高成本以及自由的面对面交流是如何推动城市化和城市体系兴起的论文。同样,假设经济由连续的单中心城市和那些技能各异的不同个人的组合体所组成。个人消费3种商品——不可交易的服务、可交易的商品和住房。个人在生产不可交易的服务或生产可交易的商品之间进行选择。城市成本等于tL/4,其中L为城市规模。在城市c中,收入水平为y的个人的间接效用水平为V(s,c)=y-npc-tL/4,其中pc(n)为非贸易品的消费价格。 不可交易的产品在规模收益不变条件下生产。相应地,个人收入水平因城市而异,且可以标准化为pc。生产可交易产品的个人的产出水平取决于他的技能和学习机会,这又取决于当地的人口组成。生产可贸易的产品的个人可以在学习和生产之间自由分配他们的时间。他们可以与任何人交流思想并向他们学习,通过与高技能个人的互动可以学到更多的技能。学习是在第四部分(一)中讨论的主要的聚集经济因素之一,在这里视它为内生的、昂贵的且因城市而异。通过提高参与思想和知识交流的个人的生产率水平,学习产生的外部性起到外生的规模收益递增的作用。 戴维斯和丁格尔的核心思想(2019)是个人技能和学习环境质量是互补的。具体地说,技能劳动力的聚集放大每个劳动力自身的生产率优势,这就是聚集力。显然,大城市的城市成本较高,因此服务也因为它必须补偿其生产者的这些较高成本变得更加昂贵,这使得作为分散力的城市成本变得更加重要。生产可交易商品的生产者只要他们的收入水平足够高,则将选择城市成本和服务成本高的大城市。当均衡时,个人选择了就业和居住的城市,且重新分配其时间以最大化其效用水平,此时所有市场全部出清。戴维斯和丁格尔的研究表明,如果城市成本并不是很高,则根据劳动力技能水平,将对空间进行分类,这与作者提供的经验证据相一致,即大城市集中大量的高技能劳动力,大城市高技能劳动力工资水平也很高。否则,与核心边缘模型中的情形一样,如果聚集力相对于城市成本较弱,则稳定均衡时,两个区域的城市规模相等。 (3)劳动力技能的互补性被伊克豪特、平海罗和施密德海尼(Eeckhout,Pinheiro & Schmidheiny,2014)发现,劳动力技能分布的标准差随城市规模的扩大而变大。具体地说,他们发现在美国大城市中,技能劳动力分布具有厚尾特征,即这些城市中的高技能劳动力和从事低水平服务行业的劳动力不成比例。因此,大城市的社会结构比小城市的社会结构更为多样化。伊克豪特及其合作者认为,异质性劳动力之间的互补性驱动了城市的空间分类。所以,核心问题是要确定何种技能组合可以共同提高他们的生产率水平以及高技能劳动力是否从与中等技能或低技能水平同事共事的过程中受益的问题。 城市全要素生产率的差异导致对技能劳动力需求的差异。伊克豪特和合作者把CES效用函数应用于生产函数中,并根据技能水平的高低顺序把劳动力分类为3种类型。然后,分别从最低技能、最高技能以及技能之间的补充或替代4种技能模式对这些3种劳动力市场绩效特征进行了评价。他们发现,如果低技能劳动力之间具有互补性(1和3),则在大城市中的劳动力技能分布显现为是低技能劳动力分布概率的厚尾特征;如果最高技能劳动力之间具有互补性(2和3),则大城市中的劳动力技能分布为高技能人才的集中;最高技能劳动力和最低技能劳动力之间的相互替代所导致的结果是相同的。上述所有这些都支持高技能劳动力和低技能劳动力之间的互补。 上述论文相得益彰。贝伦斯和他的合作者的研究表明,人口规模外部性和人口结构外部性使得劳动力技能和人口互补,从而导致劳动力技能的空间分类。戴维斯和丁格尔(2019)指出,学习的外部性会放大个人的劳动生产率水平差异,从而导致那种大城市高技能劳动力不成比例地增长以及其份额越来越大的劳动力空间分类模式。根据伊克豪特及其合作者的主张,劳动力技能的空间分类主要是由高技能和低技能劳动力之间的互补性所驱动的,这意味着大城市不成比例地承载了大量的高技能劳动力和低技能劳动力。有理由相信,上述3种观点都是有关劳动力异质性的核心思想的一部分。如果在相同框架下重新组合它们,则变为另一个议题。 不幸的是除了藤田、克鲁格曼和森(1999)的研究以外,新的城市系统模型仍然假设城市间贸易是无成本的,或者城市生产相同的商品。换句话说,无法从这些框架中识别出那些对于解释城市规模、产业结构和社会结构至关重要的城市所在的特定区位以及它所嵌入的错综复杂的贸易关系网络,因此城市也就成了一个“浮岛”。城市系统的综合性理论应清晰地解释城市区位。为此,我们必须假设运输成本的存在。事实证明,这是一项艰巨的任务,因为商品在不同城市以不同的价格销售。此外,城市规模取决于城内就业中心的出现与城际贸易流之间的相互作用,因此,应根据局部和整体力量之间的相互作用来确定生产和就业的地理区位。这是空间计量模型旨在完成的任务。 那些重点关注两个对称区域的经济地理学模型大多数都是高度程式化的框架。通过假设具有给定CBD的无特征空间,可以从影响消费者区位选择和城市布局的空间特征中抽象出单中心城市模型。解决空间不均匀性的困难以及解析维度问题的方法的缺乏,导致了新的学术领域的发展,称它为空间计量模型。 1.什么是空间计量模型 空间计量模型(QSMS)的目的是通过开发审慎对待理论问题的一般均衡框架来克服上述限制(参见德米斯特和罗西-汉斯伯格(Desmet and Rossi-Hansberg,2013)、艾伦和阿尔克拉基斯(Allen and Arkolakis,2014)、阿尔菲尔特等(Ahlfeldt et al.,2015)以及雷丁(Redding,2016)等的开创性研究)。如果利用空间计量模型,则我们可以取得比在第三部分(五)中讨论的阿拉布洛克、科泽涅维齐和舒尔曼(àla Bröcker,Korzhenevych and Schürmann,2010)的区域一般均衡模型更大的进步,甚至还能取得比在第四部分(三)中讨论的阿拉阿纳斯和刘(à la Anas and Liu,2007)的土地利用模型更大的进步。具体地说,空间计量模型主要解决在区域和城市经济学中至今还没有解决的主要的聚集力和分散力问题,例如市场准入、生产率和人口密度之间的关系以及城市成本等。当然,在研究中必须排除其他要素的影响,因此理论模型表达式是关键。空间计量模型还要解释大量的那些在基础设施水平和劳动生产率水平方面存在差异的区位。因此,这些模型被视为是促使区域和城市经济学走向综合研究的框架。 空间计量模型的主要目的并不是要提供新的理论结果,而是评估公共政策干预的影响或外生冲击的影响。为了实现其目标,这些模型接受一些外生给定的参数(例如在CES偏好下的替代弹性),而其他参数则根据观察到的变量,也就是对数据进行校准而得到。然后将模型“倒置”以从数据中查找其他不可观察到的变量的值。如果模型的参数与数据之间存在一一对应关系,则可以进行这种倒置。在这种情况下,可以准确识别出模型,并精确地确定均衡时的经济活动空间分布状况。有必要强调指出空间计量模型的一个重要的特征,即均衡必须是唯一的,且确保以模型为基础的反事实具有明确的含义。然而,具有规模收益递增或外部性特征的框架通常会显示出几种不同的均衡状态。在这种情况下,逆映射并非是唯一的。此时,可以对分散力参数施加一些限制以便控制聚集力,通过这种方式可以实现逆映射的唯一性。或者,通过向模型添加足够数量的异质性,也可以证明唯一性的存在(Herrendorf,Valentinyi and Waldmann,2000)。正如雷丁和罗西-汉斯伯格(Redding and Rossi-Hansberg,2017)所观察到的那样,拥有大量数据,则足以说明该映射是唯一的(请参见阿尔菲尔特等(Ahlfeldt et al.,2015)的论文)。 在现阶段,空间计量模型常常用来预测经济政策对均衡时经济活动空间分布的影响,这相当于对数值进行了一场无法通过分析来完成的大型的比较静态实验。空间计量模型具有几个值得肯定的优点。第一,预测考虑了模型所掌控的所有一般均衡效应,简化法是很难实现这一点的。第二,该模型可以得出定量预测。具体地说,一个理论模型可以告诉我们特定的冲击会对某些关键变量产生积极的影响,但这些模型通常无法指出这种影响强度的大小。相比之下,空间计量模型为我们提供了有关影响大小的信息,而简化法侧重于参数和变量间的定性关系。第三,使用此模型进行较大的比较静态分析,可以使人们验证从在第三和第四部分讨论的“玩具模型”中得出的结论的理论稳健性。第四,空间计量模型可以解决新的问题,例如,我们对贝伦斯等(Behrens et al.,2017)所探索的通勤和贸易摩擦如何相互作用以塑造城市系统知之甚少。正如预期的那样,通勤和贸易成本对城市规模至关重要。然而,我们没有预期的是贝伦斯等发现通勤和贸易这两种摩擦都不会显著影响美国城市规模分布。这意味着,就像在德斯米特和罗西-汉斯伯格(Desmet and Rossi-Hansberg,2013)研究中的情况一样,不断变化的空间摩擦会影响城市的相对规模,但不会显著地影响城市区位以及城市在等级体系中的地位。换句话说,空间摩擦的绝对大小不如其相对大小那样重要。 最后,不同模型彼此之间是同形的(例如内部规模经济和垄断竞争对外部规模经济和完全竞争)。在这种情况下,预测对模型簇是有效的,但对单个模型而言是无效的。例如,在完全竞争和阿明顿假设下的框架,与多个区域且内部规模经济和垄断竞争的类赫尔普曼模型的框架是同形的(Allen and Arkolakis,2014)。然而,后者与那些在规模收益不变和完全竞争框架下进行生产的伊顿和科图姆(Eaton and Kortum,2002)的模型,无法得出相同的预测(Redding,2016)。 使用空间计量模型从事研究工作的人员似乎对那些分散力主要来自每个区位固定土地供给的类赫尔普曼(Helpman,1998)模型都很感兴趣。这可能是因为该模型抓住了这样一种基本思想,即人口增长会带来更高的城市成本(参见第四部分)。使用其他模型的研究人员所强调的是基础设施和生产率方面的差异。为了说明这些,简单考虑一下下面的例子。设Ar(s)(>0)为区域r的便利基础设施存量,而在区域r的具有不同技能水平s的劳动力之间不再需要以同种方法进行分类,例如人们可能对便利设施的偏好不相同(参见戴蒙德(Diamond,2016)和(Redding,2016)的研究,他们利用离散选择模型描述了劳动力迁移)。在CES偏好下,居住在区域r的技能水平为s的劳动力的间接效用函数可以写成: Vr(s)=Ar(s)wr/Pr。 其中,wr/Pr为区域r的名义工资(CES价格指数)水平。在这种情况下,劳动力是根据其劳动生产率水平进行分类的,而居民是将依据他们对基础设施的偏好进行聚集的。 2.空间计量模型传递什么 当研究交通运输项目的影响时,空间计量模型的最大优势在于它可以考虑与新的基础设施相关的所有影响。显然,相互连接起来的区位将会受到直接的影响,而那些没有相互连接起来的区位将会受到间接影响,因为一些通过新建交通线路的交通线可能成为成本最低的线路。因此,新建的基础设施将导致劳动力在区际的重新分配。一般均衡方法的较为突出例子可以在艾伦和阿科拉基斯(2014)的研究中找到,他们建立了能够处理大量运输成本的美国的连续区位模型,在建立模型时他们考虑了所有的空间细节,包括如何选择范式的问题。他们假设生产活动是在完全竞争条件下进行,生产函数为CES偏好型函数,且阿明顿假设可以解释发生贸易的原因。艾伦和阿科拉基斯利用他们所建立的框架评估了州际公路系统的影响,而进行评估时他们重新计算了所有没有州际公路情况下的双边运输成本。研究表明,州际公路建设降低GDP总量1.1%至1.4%,这意味着州际公路系统从整体上讲是一项生产性投资,尽管这些州际公路网络设计得较差。 雷丁(2016)通过改变交通网络中某些区位之间的运输成本进行了各种比较静态的试验。根据赫尔普曼(1998)的研究,运输成本的下降促进经济活动的空间分散。雷丁根据类似于赫尔普曼的研究方法发现,如果交通条件得到改善以便影响交通网络垂直和横向路线,那么中心城市的人口趋向于下降,这使人感到很舒心。更重要的是,他利用多区域一般均衡模型进行的分析,使人们可以确定何种地区受到交通改善以及均衡时人口规模变化的积极影响或消极影响。 同样的定量方法也可以用来研究由一系列离散的街区组成的城市内部结构当受到外省冲击时发生何种影响的问题(Redding and Rossi-Hansberg,2017)。如果按照这种思路,那么对现实状况最好的解释可能来自于利用阿尔菲尔特等(Ahlfeldt et al.,2015)所建立的框架的解释。这种框架,既易于处理,又满足实证分析的需要。阿尔菲尔特等考虑了一个很好的自然实验,即柏林墙的倒塌。从第二次世界大战结束到1989年,柏林市被划分为东柏林和西柏林,它们可以被视为是被那些禁止任何交易往来的巨额的交通和通信成本所分开的两个地区性的经济体。柏林的分裂通过各种渠道影响了西柏林,包括那些就业活动高度集中在战前中央商务区和东柏林就业机会减少所导致的各种溢出效应的缺失。柏林墙的倒塌是没有预料到的突发性事件。阿尔菲尔特等把该事件作为自然实验,考察了由此产生的一对区位间距离的变化如何影响西柏林内部经济活动区位的问题。具体地说,他们的目的是从定性和定量角度解释所观察到的城市结构的变化,包括中央商务区区位的重新确定。 就我们的目的而言,以下结果值得要强调。首先,生产和消费都具有很大的空间外部性,且这些外部性是高度局域化的。其次,消费外部性比生产外部性发挥更重要的作用(15%对7%)。最后,城市内部的有关人口密度的劳动生产率弹性大大高于城市间劳动生产率弹性的估测值(7%对3%)。遗憾的是,本文中使用的各种空间外部性仍然是个黑箱。尤其,本部分所使用的聚集经济的表述,无法有效地区分出第四部分讨论的不同类型的聚集经济,且我们还不清楚聚集经济会带来何种舒适环境。 3.如何结合地理和经济增长 经济增长的作用力和地理模型中的作用力是很相似的,因此在两个领域之间存在着出现新生事物的坚实基础。然而,要求经济代理人注意经济活动总体的时空分布状况,将极大地提高问题的复杂性。此外,经济活动高度聚集也不是很合适的,因为不同的经济部门遵循不同的时空模式。因此,我们必须考虑多部门经济,这就增加了额外的难度,至今这仍是遥不可及的目标。德斯米特和罗西-汉斯伯格(Desmet and Rossi-Hansberg,2014)在其开创性的论文中提出了一种解决方法,该方法包括在模型中添加足够的结构,使得代理人在不会影响其当前决策收益的情况下忽略未来的路径。该方法的论证需要两个步骤。 (1)土地与创新。德斯米特和罗西-汉斯伯格(Desmet and Rossi-Hansberg,2012)通过证明土地是厂商做出新技术领域投资决策的关键,对此领域的研究做出了很大贡献。考虑一下单一部门经济,在该经济体中,大量的厂商利用土地和劳动力在规模收益不变生产技术下生产同质商品。空间由X=[0,1]给出。每个厂商都使用单位面积土地,且在每个区位上只有一个厂商。因此,在x(x∈X)处的土地具有不可重复使用的性质。劳动力的边际生产率递减,因此厂商的边际成本递增。结果,每个厂商都有明确的规模。厂商的生产函数是很有规矩的,生产函数可以由Q=AF(1,L)给出,其中L为劳动力工人数量,A为描述厂商技术水平的希克斯中性转换系数。请注意,创新不能通过专利形式被某一厂商所独占,但对某一区位而言是特定的。最后,获取技术A所需成本由C(A)单位产出所支付。由于土地是分配给出价最高的人,故在厂商自由进入条件下,区位x处均衡时的土地租金由下式给出: p(x)C(A)]。 其中,p(x)和w(x)分别为在区位x处的产出价格和工资水平。因此,在厂商自由进入的完全竞争环境下,厂商选择更好的技术进行投资,因为上述土地租金明确了厂商为获得这些技术而承担的成本。换句话说,通过创新,厂商可以提高对土地的竞标价格并确保最佳区位。因此,厂商对创新进行投资直到扣除创新成本的净利润等于零为止。如果土地不是生产要素,那么对于任何新的技术A,厂商将选择投入劳动力使得价格和边际成本均等,因此将导致等于p(x)C(A)的损失。在这种情况下,厂商将选择使用当前技术进行生产。 (2)空间发展。德斯米特和罗西-汉斯伯格(Desmet and Rossi-Hansberg,2014)根据上述思想建立了空间经济的动态模型,其基础是厂商通过两种不同的途径积累知识,即厂商的创新决策和附近厂商的知识溢出。 在每个周期,劳动力都可以在部门之间和区位之间自由分配,劳动力不消耗土地;有制造业部门和服务业部门两个最终产品生产部门,有土地和劳动力两种投入;厂商在每个周期都要做出生产多少以及在技术上进行多少投资的决策;商品和服务是可以进行交易的,且交易需要支付冰山交易成本;当厂商进行创新时,他们可以在本周期内获得创新的收益;在下一个周期之前,新知识是以指数衰减率在不同区位之间进行扩散的,这种知识溢出是模型中的聚集力。分散力,它主要源于土地的不可复制性,它导致厂商层面的规模收益递减;每个厂商的规模都是微不足道的,当期的创新收益只能维持一个周期并在后一个周期扩散到各个区位,因此,当期的创新决策不会影响下一个周期厂商的可用知识储备,换句话说,厂商的创新决策是静态的决策,由于生产制造业产品或服务业产品的厂商产出,随厂商可用知识储备的增加而提高,因此具有高劳动生产率水平的地区将形成多的创新,这是该地区经济增长的主要源泉。因为运输成本和技术扩散都受到距离的影响,故地理位置显得非常重要。 在现阶段,德斯米特和罗西-汉斯伯格(2014)通过借用文献中的参数值并把它处理为CES偏好下的数值的方式,对原有的模型进行了校准。校准的目的是复制1950年以来美国制造业和服务业部门的演化过程。讨论他们得出的所有结论会使我们偏离原有的目标,因此我们把讨论限制在与我们的目标直接相关的事情的讨论上。首先,该模型显示出服务行业的劳动生产率自1995年以来一直追赶制造业部门的劳动生产率,服务行业厂商的空间聚集以及由此产生的创新互动可以解释这一点。 其次,假设制造业部门厂商在空间上是聚集的(在美国,主要聚集在东北部和中西部地区),这使得这些部门厂商的劳动生产率水平很高,因为知识扩散是局域性的。相反,服务行业厂商在空间上是分散的,因此这些行业的劳动生产率水平较低。随着制造业部门劳动生产率的稳步提升,越来越多的劳动力将转向服务行业。如果制造业产品的运输成本很高,则服务行业的厂商将选择靠近制造业集群的区位,使得他们的劳动力更容易获得制造业产品。空间集中度的提高促进了服务行业厂商的技术腾飞。换句话说,很高的运输成本促使在相邻集群中服务行业和制造业厂商的聚集。随着服务行业厂商空间集中度的提高,它们的劳动生产率也因它们不断进行创新而进一步提高。结果,随着制造业部门厂商向某一区域聚集,制造业产品的相对价格逐渐下降,而服务行业产业集群规模的扩大加剧了对土地的竞争。这大大提高了制造业厂商的创新成本,从而激励这些制造业厂商向人口密度较小的地区(例如美国南部)转移。两区域的框架对于这些各种类型的模式而言局限性太大以至无法进行展开,因此也无法捕捉到厂商区位选择的动态演化过程。 最后,我们知道高运输成本通过降低专业化收益,导致静态福利的损失。但上述论证过程表明,高运输成本通过服务行业的空间聚集促进创新,从而提高了福利收益。德斯米特和罗西-汉斯伯格的数值分析表明,与高运输成本相关的动态收益补偿了静态的福利损失。简而言之,动态的多区域框架可能会得出与那些从静态的两区域模型中得出的结论完全不同的结论,例如不同于第三部分讨论的模型的结论⑦。 尽管德斯米特和罗西-汉斯伯格(2014)的模型具有很大的吸引力,但他们的模型也有一些缺陷。例如,均衡与制造业产品和服务业产品运输的相对成本无关。这就很奇怪了,因为制造业产品的运输成本通常比服务业产品的运输成本低很多,且这些服务业产品通常是不可贸易的产品。就像在罗西-汉斯伯格(2005)研究中的情形一样,个人不消耗土地,因此可以在不影响相关土地价格的情况下迁移到集群中就业。否则,集群和相邻区位附近的土地价格将会大幅度上涨,这将使相关区域的吸引力大大降低。在这种情况下,尚不清楚是否会发生两种生产部门的空间聚集。 4.空间计量模型的局限性 毫无疑问,空间计量模型的好处是很多的。但空间计量模型也是有成本的。首先,必须假定特定的函数形式。因此,结果常取决于相应的函数形式。我们认为,空间计量模型的主要缺陷之一恰恰就是重复使用相同的函数形式进行偏好设置,以至我们无法知道论文所得出的预测有多么稳健。更具体地说,CES偏好几乎无处不在。诚然,CES偏好非常方便,并且具有许多众所周知的优点,在此不予进行更多评论。但是,CES也非常独特。确实,CES偏好和冰山贸易成本相结合衍生出了许多特性,但不幸的是,这些特性难以归纳概括(Parenti,Ushchev and Thisse,2017)。是否我们应为此担心?它似乎是这样的,降低运输成本会加剧竞争,这就导致价格水平的下降和厂商数量的减少。此外,不变替代弹性是一个大胆的假设,它忽略了新产品进入挤占产品特性空间使得不同种类产品更容易替代的事实(Salop,1979)。在这种情况下,替代弹性随着产品种类数量的增加而变大,从而出现与厂商进入有关的替代竞争的效果。垄断竞争的CES偏好模型无法解释这些最重要的效应。 其次,通常利用柯布-道格拉斯型(C-D)效用函数嵌套不变替代弹性型(CES)效用函数的形式。在C-D型和CES型效用函数的结合下,整个经济系统中某一部门受到冲击所造成的福利影响,仅限于在该部门直接福利效应方面。然而,人们可以预测,对某一部门的正向冲击将导致财政预算和劳动力在所有部门之间的重新配置。这就等于对一般均衡效应施予了一些限制条件。 最后,CES偏好效用函数具有一些特殊的属性,即在单一部门经济中,垄断竞争结果是社会最优的。但在多产业的经济中,资源在部门间的重新配置不再是最优的,因为不同市场之间的相对价格会被扭曲,而同一市场内的相对价格则不会变化,因此这种最优属性不再成立。但这有关系吗?答案是肯定的。贝伦斯等(Behrens et al.,2016)提供的案例说明,这种组合会带来可能的福利偏差。他们分别考虑了具有CES偏好和不变绝对风险规避(CARA)偏好的多部门垄断竞争模型,然后评估了因价格提升而导致的部门内和部门间的福利损失。贝伦斯等通过量化法国和英国数据而建立的CARA和CES模型发现,在CARA偏好下的总福利损失为6%~8%,而在CES偏好下的福利损失要低得多(不到1%)。 简而言之,空间计量模型主要依靠那些明确理论假设下的框架,这使得此方法是非常可取的。少量的那种把准自然实验作为识别策略的论文表明,这些数据不会拒绝CES偏好(Redding and Sturm,2008;Donaldson,2018)。然而,对模型进行精确校准时,功能规格选择不当容易被忽视。因此,当结构化的方法系统地使用相同的特定模型时,质疑结构方法的有效性并非没有道理。在计算能力和数值方法迅速发展的时代,应该对函数形式进行稳健性检验。 我们尽力对不同类型的文献进行综述,就是要说明一般均衡思想可以回答引言中提出的一些问题,以及许多其他一些问题。在这种过程中,我们常常遇到规模收益递增与商品、人员和信息流动障碍间的权衡问题,而这两者都以不同的形式出现。然而,尽管有这种共同的脉络,但空间经济学仍在寻找一个涵盖区域、城市和交通经济学的总体框架。这些问题相当复杂,因此这种探索很可能会持续到很长时间,这就是要求我们应采取谦虚而认真的态度的主要原因。 那些简单且程式化的框架的分析能力问题已得到解决了,这些框架对于理解各种效应如何相互作用是非常有用的。这种模式的优点是它们带来了前沿的和新的重要成果,这源于区域和城市经济学的融合。从这种角度来考虑,则赤松等(Akamatsu et al.,2017)的研究是大有前途的,他们将不同的模型连接在一个统一的框架结构内,而这种框架结构只依赖于两类基本的分散力,这使得他们可以在更加一般化的环境中预测运输成本的影响。空间计量模型能够从更广阔的视野解决相同的问题。不幸的是,一般均衡结果难以证明,而从简单框架中获得的主要结论又无法推广到异质性空间环境中。除其外,空间计量模型也可以用来检验从简单模型得出的结果的相对稳健性。 我们同意霍姆斯(Holmes,2010)的在实证研究中应采取谦虚而认真的态度的主张。尽管结构性方法因考虑一些一般平衡效应而比较可取,然而对那些估算关键参数的简化型方法而言,还存在许多改善的空间。毕竟,在空间计量模型中使用的一些结构性参数通常借用其他论文估算出来的数值。我们还需要一个更加系统性的结果确认方法,并在某种程度上说,有必要更加系统地研究从一系列致力于研究聚集经济、聚集不经济以及交通运输项目影响的实证研究中得出的结论的稳健性问题。 解决代理人的流动性问题是以极端假设为前提的。大量的区域和城市经济模型假定每个个体的偏好相同且流动无成本,而运输经济学通常假定代理人区位是固定的,这些都是对这些问题把握得很不充分的表现。符合实际的居住转移成本模型更有助于人们更好地理解空间格局的演变过程。大多数为该领域发展做出贡献的研究也假设厂商和劳动力是一起转移的,然而没有迹象表明厂商转移和劳动力个人转移都遵循相同的规则。因此,研究那些包括厂商和个人反应模式不相同在内的模型的稳定状态,将成为该研究领域的重大补充。 众所周知,在偏好相同的代理人假设下得出的经济领域的许多研究结果都缺乏稳健性。例如,厂商异质性对于理解厂商在国际市场上的行为以及不同政策的含义是至关重要的。消费者异质性与厂商异质性同样重要,应对那些已经包括计量空间模型的离散选择模型给予更多的关注以便更好地把控消费者个体的异质性特征。还需要研究新的分析工具,例如博弈分析已被证明对研究交通量拥堵(Beckmann,McGuire and Winsten,1956)和核心边缘模型研究(Oyama,2009)是非常有用的。需要在这些博弈模型方面进行更多的研究⑧。 我们认为,空间经济学已经发展到相当成熟的阶段,进而也可以进行学科间的交叉。莫雷蒂(Moretti,2011)和泽诺(Zenou,2009)的研究位于劳动和空间经济学的交叉点上,他们的研究为可以通过合并不同领域来进行研究提供了富有启发性的案例。人们想知道,为什么城市和区域经济学与交通运输经济学之间的差距还是这么大。例如,住房和当地劳动力市场与运输市场是紧密交织在一起的。此外,这些议题还具有重要的政策性含义。目前在城市经济学如何加强在城市规划中的烙印以及城市规划如何影响城市经济学等方面的研究,仍然相当缺乏。 运输经济学家应该更多地关注与新的运输基础设施建设有关的各种类型的益处,而区域和城市经济学家应该更多地关注运输网络的作用。空间经济学家不应把交通运输部门视为黑匣子,而应把它视为具有特殊属性的产业部门。此外,几乎无处不在的冰山成本假设,忽略了密度经济和距离经济在交通运输成本中的重要作用。交通经济学家还期望区域和城市经济学家帮助他们评估交通基础设施项目在现实中的具体区位和具体福利影响。在此方面的案例很多,包括美国新的运输基础设施建设、巴黎快车道等大型公交基础设施建设,中国西部地区公路建设以及欧盟委员会讨论的一系列运输项目建设等。 最后还得进行评论,经济发达和经济欠发达是经济活动块状分布的一个方面。本综述所涵盖的所有资料都与那些国家土地所有权、专利、建筑管理当局等机构运作良好,以及政府提供必要的基础设施等经济状况较为正规的国家有关,这对于贫穷国家或富裕的国家以及19世纪还是在20世纪都是如此(Glaeser and Henderson,2017)。然而,当经济是非正规且市场机构不能很好运作时,我们需要新的模式。 注 释: ①参见格莱泽和梅勒(Glaeser and Maré,2001)、莫雷蒂(Moretti,2012)和戴蒙德(Diamond,2016)对美国的研究,库姆斯、杜兰顿和戈比伦(Combes,Duranton and Gobillon,2008)对法国的研究,米仰和纳惕齐奥尼(Mion and Naticchioni,2009)对意大利研究,吉本斯、奥弗曼和佩尔科嫩(Gibbons,Overman and Pelkonen,2014)对英国的研究。 ②聚集经济的思想可以追溯到马歇尔(Marshall,1890)。产业内外部经济被称为地方化经济或马歇尔-阿罗-罗默(MAR)外部性,产业间外部经济被称为城市化经济或雅各布斯外部性。这些概念有时成为混乱之源泉。 ③国家间溢出效应也随距离而递减(Keller,2002),它们常常通过国际贸易、外国直接投资等不同的途径溢出。 ④亨德森(2003)通过检验厂商总要素生产率是否受到相邻厂商密度的影响的方式,开拓性地建立了不同的研究途径。 ⑤藤田(Fujita,1989)的里程碑式的著作给出了有关单中心城市模型最好的总结性评论。杜兰顿和普加(Duranton and Puga,2015)最近对城市土地利用模型进行了最详尽的综述。 ⑥著名建筑物的大量存在也起到阻碍城市发展的作用。霍恩贝克和凯尼斯顿(Hornbeck and Kenistin,2017)的研究显示了波斯顿1872大火炬塔是如何为新建筑物的建设提供发展机会的情形。 ⑦德斯米特和罗西-汉斯伯格(Desmet and Rossi-Hansberg,2015)利用类似于上面的模型研究了气候变化对农用土地和工业用土地的影响。 ⑧许多研究者忽略了许多空间模型在总体博弈方面具有特定结构的事实。这种总体博弈是指与那些具有有限数量的纯战略集合、连续支付矩阵的大量的小型或匿名参与者(厂商或劳动者)进行博弈。这种博弈总有纯战略的纳什均衡,并显示为比较灵活(Sandholm,2010)。(三)交通拥挤成本
五、走向区域和城市经济学的综合
(一)城市体系,或者所有城市为什么不相同
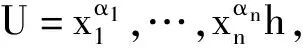
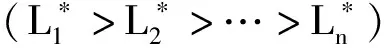
(二)空间计量经济学
六、结束语

