考虑落角约束的制导炸弹有限时间控制制导律

穆忠伟，吴 剑，韩秀枫

(南昌航空大学信息工程学院，南昌 330063)

0 引言

制导炸弹的发展始于第二次世界大战后期，经过数十年的改进与创新取得了长足的发展，具有结构简单、使用方便、射程远、命中精度高、造价低、费效比高等优点，是世界各国机载高精度武器中数量最多的一款空地武器[1]。制导炸弹在现代战场中作为一种精确性极高的制导武器，主要用于攻击地下或地面的坚固目标。未来信息化战争是敌对双方在陆、海、空战场的对抗，将使制导炸弹的需求数量显著增加。制导炸弹作为一种精确的制导武器，其制导律的研究越来越重要，目前的制导需求越来越集中在约束条件上，例如脱靶量、攻击落角、消耗能量、过载及攻击时间等，从而提高了制导炸弹对目标的破坏效能。近年来，一些学者基于不同的理论方法提出了诸如最优制导律、滑模变结构制导律、改进型的比例导引律及其他类型的一些制导律[2]。

文献[3-5]针对拦截机动目标的过程中考虑攻击角度约束的制导问题，都提出了一种考虑导弹自动驾驶仪动态特性的制导律。文献[6-9]提出了关于积分滑模控制的制导律。文献[10]根据精确打击及高效毁伤的指标要求，面向地面的目标，提出了一种满足末端位置、落角及攻击角度约束的最优导引律。文献[11-13]主要是针对有限时间收敛的制导律方面的研究。文献[14]主要是基于多项式函数推导出的具有落角约束的制导方法。文献[15]主要针对导弹攻击机动目标的要求，约束攻击角度，利用滑模变结构控制理论，提出了一种同时满足脱靶量为0和攻击角度约束要求的制导律。

本文基于终端滑模控制方法，选取包含炸弹前置角和落角约束项及脱靶量约束项作为滑模面切换函数，并结合自适应趋近律，设计了一种带落角约束的有限时间控制制导律。该制导律不仅可以使炸弹在有限时间内收敛到期望的攻击角度，而且还有一定的外内部干扰的能力，最后通过仿真验证了此制导律的有效性。

1 弹目相对运动建模与分析

研究制导炸弹的制导律时，需要建立导弹和目标之间的相对运动关系模型。而制导炸弹在飞行过程中，滚转通道处于稳定的状态，弹体的滚转角比较小，可以近似为0。本文仅对纵向平面的情况进行分析，分析的结果同样适用于侧向平面。假设导弹和目标均视为在平面运动的质点，图1给出了导弹和目标的相对运动关系。

图1 纵向平面内弹目相对运动关系Fig.1 Missile-target relative motion relationship in longitudinal plane

在图1中，B表示制导炸弹；T表示目标；Vm为炸弹的速度，Vt为目标的速度；r为目标和炸弹的相对距离；q为弹目视线角；θm和θt为炸弹和目标的弹道倾角。取η为炸弹的速度前置角。

制导炸弹与目标的相对关系方程为

(1)

令炸弹的期望落角为θd(t)，期望的终端视线角qd与目标运行速度倾角θt(t)的关系可表示为

θd(t)=θt(t)+ρ

(2)

对于给定的θd和θt，存在如下的关系[16]

(3)

由于制导炸弹主要是用来攻击地面的固定目标或机动性很弱的目标，假设目标的机动性可以忽略不计，令Vt和θt为0。则式(3)可以简化为

(4)

分别对式(1)中两项左右进行微分，整理得出

(5)

(6)

2 有限时间收敛的预备知识

为了便于下文对导引律有限时间收敛特性的分析和证明，要求系统在有限时间内收敛，因此对有限时间控制理论进行了简要的介绍。

考虑如下非线性系统

(7)

式中：f:U0×R→Rn在U0×R上连续；U0是原点x=0的一个开邻域。

引理2[18]对于系统(7)，若存在连续、正定函数V(x)满足

(8)

式中：d,e>0;0<γ<1均为常数。对于给定的初始状态x(t0)=x0,在有限时间内V(x)≡0,系统状态到达稳定点的时间t取决于初值x(0)=x0,且满足不等式

(9)

即系统状态是在有限时间收敛的。

3 带落角约束的有限时间控制的制导律设计

3.1 稳定性及有限时间收敛特性分析

首先利用非线性控制系统的有限时间收敛性理论和终端滑模变结构控制理论，分别对制导系统的滑模面趋近和沿滑模面运动的2个阶段进行有限时间收敛证明。

针对弹目视线角速率在制导末端变化剧烈的问题，同时考虑制导炸弹以特定的入射角命中目标的性能指标，设计终端滑模面的切换函数为

s=η+k1|x1|αsgn(x1)+k2x2

(10)

式中：0<α<1,k1、k2>0,等式右边的第一项，θm-q=η,当η=0时，即q=θm,则弹目弹道倾角方向和弹目视线方向是一致的，炸弹能够命中目标，且弹道较为平直；第二项为落角约束项，可满足期望入射角要求，能够保证以一定落角约束命中目标；第三项可以满足弹目视线角速率趋近于0，进一步保证命中的精度。

对式(10)两端进行求导，可得

(11)

为保证有限时间到达滑模面，并且满足系统状态轨迹的到达条件和具备良好的动态特性，以及考虑控制系统的时变性，构造自适应趋近律为

(12)

式中：ε，λ>0。该趋近律的自适应性主要体现在滑模面切换函数向滑模面运动的速率随着r的变化进行自适应调整。在末制导开始阶段，弹目距离r比较大，趋近的速率较慢，制导指令的合理分配可有效避免制导指令出现饱和；当弹目距离r越来越小时，趋近的速率迅速增大，促使s收敛到0，避免发散。对式(12)的自适应趋近律进行滑模可达性分析，将其两边各乘以s，可得

(13)

满足系统的状态运动到滑模面上。

针对制导系统到达滑模面的过程，对所构造的函数进行有限时间收敛分析。选取Lyapunov函数为

V1=s2

(14)

对式(14)求导并结合式(13)，可得

(15)

求出式(14)中的s,可得

(16)

将式(16)代入式(15)中,可得

(17)

根据引理(1)可知，制导系统在有限时间内可收敛到滑模动态面s=0。

对系统沿着滑模面运动阶段进行分析，滑模面满足如下条件

s=η+k1|x1|αsgn(x1)+k2x2=0

(18)

根据式(6)可得

(19)

利用Lyapunov稳定性原理证明式(19)是稳定的,并使视线角收敛到期望的视线角，取Lyapunov函数如下

(20)

对式(20)进行求导并结合式(19)，其中令η=(q-qd)e-r=x1e-r，可得

(21)

由式(20)可得

(22)

将式(22)代入式(21)中,可得

(23)

根据引理2可知，系统沿着滑模面的运动是有限时间收敛的。

3.2 带角度约束的有限时间控制制导律设计

联立式(11)与式(12)可得

(24)

由于制导炸弹所攻击的对象是弱机动或固定的，所以将at作为外部干扰项而忽略。将式(24)代入式(6)中,可得

am=

(25)

令式(1)中的vt=0,可得

(26)

对式(26)求解后,可得

(27)

对式(27)求导,可得

(28)

(29)

将式(29)代入式(25)可得出最终的制导律为

(30)

4 弹道仿真与结果分析

为了验证本文提出的制导炸弹有限时间控制制导律的有效性，采用比例系数K=5的经典广义比例导引制导律

(31)

进行对比仿真验证。设炸弹的初始位置为Xm=0m,Ym=4000m;炸弹飞行的速度Vm=260m/s,初始弹道倾角θm=0°。目标的初始位置为Xt=4800m,Yt=0m;目标为静止目标，Vt=0m/s。参数设置为λ=0.1，α=0.1，ε=0.8，k1=12,k2=1.75。设炸弹以垂直角度攻击目标为例，仿真结果如图2～图6所示。

图2 制导炸弹的弹道轨迹Fig.2 Trajectory of a guided bomb

首先由表1可以看出，有限时间控制制导律的制导时间是26.97s，大于比例导引的制导时间24.7s，是因为带角度约束的有限时间控制制导律的制导弹道曲线要比传统的比例导引律的制导弹道曲线要高(如图2所示)。然而在实际情况中，抬高的弹道可以为炸弹提供更快的攻击速度，增大毁伤效能。从脱靶量来看，有限时间控制制导律的脱靶量是0.2585m，而比例制导律的脱靶量要达到1.4519m，可以看出本文所提出的制导律使制导炸弹具有更高的制导精度，脱靶量也非常小。

表1 两种制导律制导效果的比较Tab.1 Comparisons of guidance performance between two laws

从图3可以看出，制导炸弹约束以90°角攻击目标，有限时间控制制导律的实际落角误差是0.0052，而比例制导律的偏差为40.2685。很明显可以对比出，有限时间控制制导律几乎以90°角攻击目标，命中角度很精准，毁伤效能很强。

图3 弹道倾角Fig.3 Trajectory inclination angle

从图4可以看出，当落角约束比较大时，炸弹越接近目标，炸弹的法向加速度幅度越大，炸弹的需用过载越大，但最终收敛于0附近，展现出本文制导律具有良好的收敛能力。

图4 纵向平面内炸弹法向过载曲线Fig.4 Normal overload curves of guided bomb in longitudinal plane

图5给出了视线角随时间的变化曲线，图6给出了视线角变化率随着时间变化的曲线。

图5 视线角曲线Fig.5 Line of sight angle curve

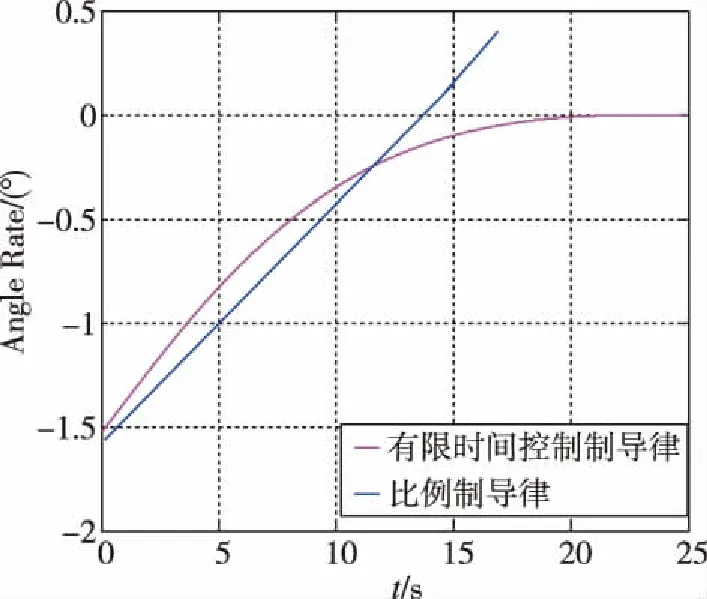
图6 视线角速度变化曲线Fig.6 Line of sight angular velocity curves

5 结论

本文运用变结构理论与有限时间稳定性理论相结合的方法，提出了一种带落角约束的制导炸弹的制导律。该制导律不仅能够使炸弹在末制导阶段的系统状态轨迹快速地到达滑模面，还能够在有限时间内收敛；而且该制导律选取的切换函数使得炸弹能够比其他制导律更加精确地命中目标，并能够满足入射角的约束，使炸弹的视线角及其角速度收敛得更快；同时还能够大幅度地提升制导武器的制导效能，并具备很好的工程适用性。