基于地球坐标系的SINS/GNSS极区组合导航算法

张甲甲，卞鸿巍，王荣颖，马 恒

(海军工程大学电气工程学院，武汉 430033)

0 引言

极区冰层的快速减少，使北极航道逐渐成为新的海上交通动脉。随着对极区导航问题的日益重视，人们针对传统的力学编排方案在极区不再具备导航能力的问题，提出了诸多适用于极区导航的惯导力学编排方案，如极区平面导航、极区格网导航、横向坐标系导航[1]等。然而无论哪种形式的惯导编排，都会表现出惯导固有的特性，如稳定性、振荡性以及对初始条件做出的响应[2]，这些特性对惯导系统精度将产生严重影响。

为保证舰船在极区可以长航时高精度工作，国内外学者对极区阻尼及组合导航技术进行了相关研究[3-8]。文献[3]提出了适用于极区的横坐标系捷联惯导系统(Strapdown Inertial Navigation Sy-stem，SINS)阻尼技术；文献[4]参考传统指北方位惯导力学编排方案，提出了一种基于横坐标系的SINS/多普勒计程仪(Doppler Velocity Log，DVL)组合方案；文献[5]在格网坐标系框架下推导了格网惯性力学编排方程和导航误差方程，结合星跟踪器的输出提出了惯性/星跟踪器极区组合方案；文献[6]提出了极区游动坐标系下的惯性导航系统(Inertial Navigation System，INS)/全球定位系统(Gl-obal Positioning System，GPS)组合导航方案。但是，文献[3-5]的惯导编排都是基于地球球体模型的，存在原理性误差；文献[6]提出的组合导航方案不具有穿越极点的能力。

综上所述，本文结合全球卫星导航系统(Global Navigation Satellite System，GNSS)全球性和高精度等优点[9-10]，研究了一种基于地球坐标系的SINS/GNSS极区组合导航算法，在地球椭球模型的框架下定义了横向坐标系，将地球坐标系确定为惯导计算坐标系，卡尔曼滤波器估计的姿态、速度和位置误差是相对于地球坐标系的，再将地球坐标系下的导航结果转换到横向坐标系。相对于当地水平坐标系算法，地球坐标系下的捷联算法和卡尔曼滤波算法在保证导航精度的情况下，计算效率可以分别提升40%和10%[11]，对实现高精度的导航及滤波算法十分有利。结果表明，地球坐标系下的组合导航算法满足极区航行的需求。

1 基于地球椭球模型的横向坐标系设计

如图1所示，定义0°经线和180°经线组成的大椭圆为横向赤道，取90°E经线和90°W经线的北半球部分组成的半个大椭圆为0°横向经线，定义原地理坐标点(0°，90°E)和(0°，90°W)分别为横向北极点和横向南极点。横向地球坐标系与地球固联，取地球椭球体模型的中心作为坐标原点，X′ 轴指向传统北极N，Y′ 轴指向格林尼治子午线与赤道的交点,Z′ 轴指向横北极点。

图1 椭球横向坐标系Fig.1 The transversal coordinate frame based on the earth ellipsoid model

地球表面上任意一点P的横向纬度定义为地球椭球面外法线与横向赤道面的夹角，其横向经度为地球椭球面外法线在横向赤道面上的投影与OX′ 轴的夹角。定义横向地理坐标系(n′)的横地向轴D′沿参考椭球体的法线方向，横北向轴N′在垂直于D′轴的平面内，指向横北极的方向，根据右手定则确定横东向轴E′。

根据以上定义，利用几何关系可以得到横向经纬度与地球坐标的关系为

(1)

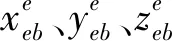
依据传统经纬度与地球坐标的关系为

(2)

可得，传统经纬度与椭球横向经纬度的变换公式为

(3)

根据式(3)，RN用横向经纬度表示为

(4)

式中，R0为赤道半径。

惯导系统直接输出地球坐标系下的导航参数，经过以下变换可得到横向地理坐标系下的导航参数。根据定义可以得横向地球坐标系与横向地理坐标系的坐标转换矩阵为

(5)

从地球坐标系到横向地球坐标系的坐标转换矩阵为

(6)

由式(6)可以得到,地球坐标系到横向地理坐标系的坐标转换矩阵为

(7)

则横向地理坐标系下的速度为

(8)

横向地理坐标系下的姿态矩阵为

(9)

由式(1)可得,由地球坐标系下的位置到横向地理坐标系下的位置的计算式为

(10)

由于式(10)中等式右侧包含L′、λ′、RN项，且RN是横向经纬度的函数，故式(10)需经过多次迭代才能得到。一般可取前一时刻的横向位置作为迭代初值。

2 地球坐标系下的惯导编排

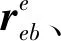
(11)

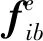
(12)

(13)

其中，μ为地球引力常数，取值为3.986004418×1014m/s2，J2为地球第二引力常数，取值为1.082627×10-3[13]。

惯性导航系统误差模型不仅是系统误差分析与控制的基础，而且还可用于系统中实时故障检测和卡尔曼滤波的执行。捷联惯导系统在地球坐标系下的误差模型可表示为[14]

(14)

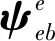
(15)

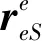
3 地球坐标系组合导航算法

在本文研究的SINS/GNSS组合导航系统(见图2)中，捷联惯导系统选用地球坐标系作为导航解算坐标系，卫星导航系统直接输出地球坐标系下的位置和速度信息作为量测量输入到卡尔曼滤波器，对SINS误差进行估计。将滤波器估计的SINS误差反馈到惯导系统中对导航参数进行校正，再对校正后的地球坐标系下的导航参数进行导航信息转换，得到横向地理坐标系下的导航参数构成组合导航系统输出。

3.1 系统状态方程

(16)

根据式(14)可得系统状态方程为

(17)

式中，ws为系统噪声向量，G为系统噪声分布矩阵，系统矩阵F表示为

(18)

其中

(19)

3.2 系统量测方程

将GNSS测量的地球坐标系下的载体位置、速度与惯导输出的位置、速度的差值作为观测量，建立量测方程为

(20)

则量测方程的矩阵形式为

z=Hx+wm

(21)

式中,wm为量测噪声，用I3表示三阶单位阵，测量矩阵近似为

(22)

4 仿真验证

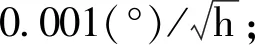
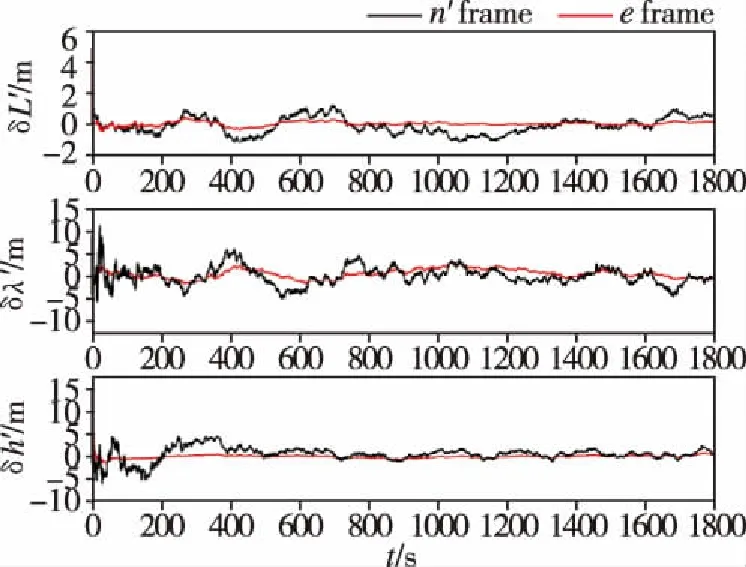
图3 横向位置误差对比Fig.3 Comparison of transverse position errors

图4 横速度向误差Fig.4 Comparison of transverse velocity errors

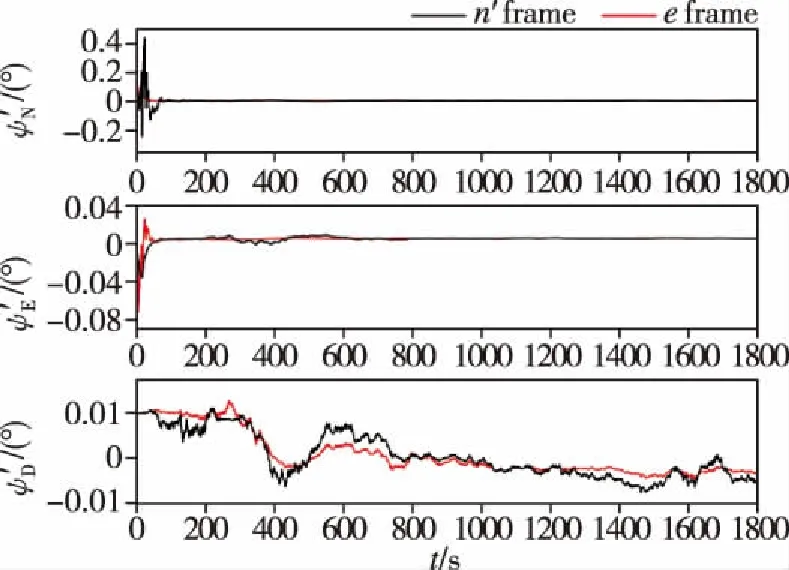
图5 横向姿态误差对比Fig.5 Comparison of transverse attitude errors

由图3～图5可得，在1800s的仿真时长内，两种组合导航方法输出的横向地理坐标系下的导航信息均获得了较好的收敛效果。基于地球坐标系的SINS/GNSS极区组合导航方法的横向定位误差不超过2m，横向速度误差不超过0.02m/s，姿态精度达到0.4′。在1100s左右穿过极点时，各导航信息未发生跳变，系统十分稳定。其中地球坐标系下的组合导航方法得到的位置和航向精度优于横向地理坐标系下的组合导航方法，且输出导航信息更加稳定。这是因为在极区范围内，地球表面形变较大，不能很好地与地球椭球模型吻合，而地球坐标系下的组合导航方法脱离了地球椭球模型假设，具有更高的导航精度。由此可以看出，本文研究的组合导航系统能有效解决极区环境下惯性导航系统误差随时间积累的问题，满足极区航行作业的需求。

5 结论

本文研究了一种基于地球坐标系的极区SINS/GNSS组合导航算法，给出了横向坐标系的定义，建立了地球坐标系与横向坐标系之间的转换关系。捷联惯导系统的计算更新在地球坐标系下完成，将GNSS测量的地球坐标系下的载体位置、速度与惯导输出的位置、速度的差值作为观测量进行滤波估计，最后将解算结果转换到横向坐标系下。算法在保证导航精度的情况下，大幅度提升了计算效率。仿真结果表明，该算法满足极区航行的要求，并且在舰船穿越极点时，也可提供高精度的导航信息。