基于蚁群算法西安旅游路线的优化研究
李梦丹
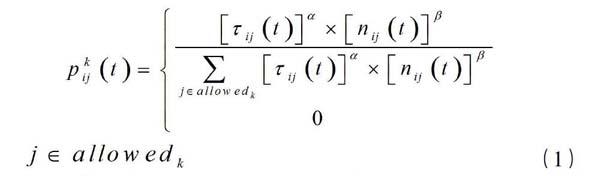
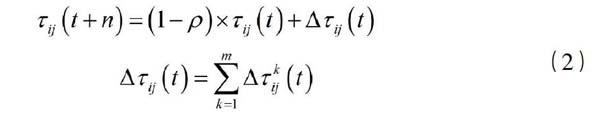

摘要:随着人民需求的日益增长,出外旅游成了生活的一部分。但是如何规划旅游线路节省时间使路径最短是论文考虑的问题。文章利用matlab软件通过蚁群算法对西安著名的16个景点进行了路径规划,实例证明,蚁群算法在解决路径优化这类问题是相对有效的。
Abstract: With the increasing demand of the people, traveling abroad has become a part of life. But how to plan the travel route to save time and make the route shortest is the issue considered by the thesis. The article uses matlab software to carry out path planning on 16 famous scenic spots in Xi'an through ant colony algorithm. The example proves that the ant colony algorithm is relatively effective in solving such problems as path optimization.
关键词:蚁群算法;最优路径;matlab软件
Key words: ant colony algorithm;optimal path;matlab software
中图分类号:F252 文獻标识码:A 文章编号:1006-4311(2020
0 引言
随着科技的发展,互联网技术使得网上订酒店车票非常方便,利用各类app进行查询旅游景点相当方便,所以随着生活水平的提高,自助游将会越来越受到人们追捧。人们会根据出行的时间合理的规划旅游行程,选择合适的景点个数,但是实际出行中,还会伴随其他问题的产生,例如旅游路找的规划、旅游费用等,这个时候需要合理的方法解决这个问题。许多学者对这个问题进行研究,最早源于TSP旅行商问题[1],随后对该问题的算法进行深入研究,解决这类问题常用的方法有蚁群、粒子群、遗传算法等等。论文结合蚁群算法,对陕西省著名旅游景点进行路径规划,蚁群算法可以为我们提供最佳的旅游顺序。
1 算法介绍
蚁群算法(Ant Colony Optimization,ACO)于1992年由Marco Dorigo提出,来源于实际生活中蚂蚁寻找食物过程中发现路径的行为,最早用来解决旅行商问题[2]。
如图1所示,有两条路线,ABD和ACD,其中ABD是一条直线,ACD是一条曲线,ACD长度是ABD长度的两倍,C点是曲线ACD的中点。假设有两只蚂蚁分别为a、b,蚂蚁a采取ABD路线,而蚂蚁b采取ACD路线。同时从A地出发赶往D然后再回A地。当a到达D时,b正好到达C,当a从D回到A时,b正好到达D。此时残留在ABD途径中的激素是ACD途径中的激素的两倍[3]。
算法相关规则主要包括两种:
①路径转移规则。
开始状态,每只蚂蚁被随机放到其中的一个城市上,第k只蚂蚁在t时刻从城市i到城市j的转移概率为:
式(1)中,τij(t)表示t时刻路段(i,j)户上的信息素的量,在初始时刻各条路径上的信息量相等,即τij(0)=常数,nij(t)为启发函数,nij(t)=■。dij表示路段(i,j)的长度。allowedk表示蚂蚁可选择的节点集,α表示轨迹相对重要性的信息启发因子,β表示能见度相对重要性的期望启发因子。
②轨迹更新规则。
在迭代过程中,蚂蚁需要使用本地更新规则在移动的每个步骤中更新相应路径上的信息素浓度,更新规则如式(2)所示:
式(2)中ρ表示信息索挥发系数,且ρ的取值范围为ρ∈(0,1),由于信息素更新策略的不同,全局搜索能使我们得到更好的解决方案,因此采用如式(3)所示的全局信息索更新规则:
式(3)中,Q表示蚂蚁循环一周时在一定程度积累的信息素总量Lk表示本次循环中,蚂蚁k所走路段的长度[4]。
2 实例验证
2.1 实例介绍
陕西省是一个具有浓厚历史韵味和人文特色的著名旅游城市,论文选取陕西省16个著名景点作为分析对象,其中包含自然景观、历史遗址、现代建筑等等相对具有代表性的旅游景点。其中包含秦始皇陵及兵马俑、华清池、大雁塔、唐长安城大明宫遗址、城墙永宁门、钟鼓楼、回民街、小雁塔、大唐芙蓉园、陕西历史博物馆、西安世博园、白鹿原、西交大(曲江)、西工大、马嵬驿、华山等16个景点。这些景点有些分布陕西省城区,有些分布在西安市内,分布不一,如果没有做好规划,会造成路线的重复,这样既浪费时间,又增大成本,因此应重点对旅游的顺序进行一个简单的排序,论文以距离最小化为求解目标,展开西安旅游景点的路径规划。
景点坐标如表1所示。
2.2 matlab结果分析
文章所表示的距离,是用地理坐标直接计算,换算为实际距离需乘以地球半径,这里简单处理,得出旅游顺序即可。通过matlab结合蚁群算法,对旅游路线进行规划迭代。
将表中的数据写成的矩阵形式导入到MATLAB中,蚁群算法中种群数量设置与城市的个数相对应为16。根据若干次MATLAB仿真试验结果对蚁群算法的其他参数进行设定:激素重要程度参数设置为1,启发因子重要程度参数设置为5,激素蒸发系数设置为0.1,激素增强系数为100,最大迭代的次数设置为200,利用同样的参数和程序对西安市旅游景点进行多次MATLAB仿真计算。最优结果如图2所示。
最短距离:3.7215(地球半径)
最短路径顺序:7—4—6—5—10—3—8—9—13—11—2—1—16—12—14—15—7
3 结束语
路径优化是实际中一个很常见的问题,在生产调度,资源优化等等问题中都有较多的应用,而论文对旅游线路的规划也具有一定的实际意义。通过多次调整,最终实现路径最短,迭代最快,达到我们所要实现的目标。但是论文对于实际中的费用等因素没做考虑,今后的研究应重点针对实际影响因素,这样蚁群算法可以更好地解决实际问题。
参考文献:
[1]邹腊英.基于TSP问题的旅游路线安排[J].兰州文理学院学报(自然科学版),2015,29(05):23-25.
[2]肖艳秋,焦建强,乔东平,杜江恒,周坤.蚁群算法的基本原理及应用综述[J].轻工科技,2018,34(03):69-72.
[3]开吉,杨金云,蒋其岑,王玉琴,开晶晶.基于蚁群算法的物流配送路径的研究[J].物流工程与管理,2018,40(02):74-76.
[4]万慧云,蒋艳.基于蚁群算法的5A景点旅游路线规划问题研究[J].软件导刊,2019,18(04):141-144.

