水流作用下悬浮隧道耦合动力数值模拟分析

郭晓玲，金瑞佳，刘名名，耿宝磊

(1.国家知识产权局专利局专利审查协作天津中心，天津 300304；2.交通运输部天津水运工程科学研究所 港口水工建筑技术国家工程实验室 工程泥沙交通行业重点实验室，天津 300456；3.中国海洋大学，青岛 266100；4.成都理工大学，成都 610059)

水下悬浮隧道(Submerged Floating Tunnel，简称SFT)作为一种跨越海峡、海湾以及湖泊等的新型交通结构物，通常悬浮在水下方30 m左右。水下悬浮隧道内部空间较大，足以满足公路甚至铁路等交通方式的要求。有些自然条件十分恶劣的峡湾，由于环境条件及技术的限制，传统的跨越方式(如：跨海大桥、沉管隧道)并不可行，而SFT提供了跨越的可能性。耿宝磊等[1]对悬浮隧道水动力问题进行过概述，指出对于工作水深较深的悬浮隧道而言，波浪对其影响较小，而水流对其影响较大。

1 研究背景与现状

针对水流与悬浮隧道的耦合动力分析，很多学者都有过相关研究。麦继婷[2]考虑流固耦合效应，研究了表面流速、隧道断面形式和支撑形式对悬浮隧道动力响应的影响。分析发现，表面流速会显著影响悬浮隧道系统的响应位移，但基本不影响沿隧道轴向的应力分布形态。王广地[3]分析了海流横向升力作用下悬浮隧道结构所受荷载随悬浮深度、海水深度、海流速度以及管段截面尺寸等参数的变化规律。龙旭[4]研究了不同的浮重比下水中悬浮隧道的动力响应，给出选用模型的水中悬浮隧道在水流载荷下的最优浮重比范围。上述研究在讨论水流荷载时，均采用基于Morison公式的升力经验公式，并未详细考虑悬浮隧道对流场的影响。为了准确描述水流经过悬浮隧道后流场的变化，罗刚等[5-6]通过基于大涡模拟(Large Eddy Simulation, LES)的方法在数值上分析比较了断面形式不同、来流速度有差异以及迎流面宽度也不尽相同的情况下固定式悬浮隧道所受的流体作用力及周围流场分布情况，研究发现耳形断面形式悬浮隧道结构物具有最好的稳定性，并且其升力系数和阻力系数较小，是最为合理的截面形状，然后依次为圆形、椭圆、六边形和矩形。

由于悬浮隧道通过锚泊系统悬浮在水中，在流体作用力下就会发生运动，周期变化的升力使弹性支撑的悬浮隧道在垂直于水流方向发生振动，也就是“涡激振动”(Vortex-Induced Vibration，VIV)。当涡脱落的频率接近悬浮隧道结构的自振频率时，共振或者说锁定(Lock-in)现象将会发生。锁定的发生同时意味着结构发生了最不愿意出现的共振现象，此时运动振幅将明显增大，更会显著增大结构的疲劳损伤程度，从而对工程安全造成不利影响。国内外很多学者对涡激振动问题开展了实验研究和数值模拟。Feng[7]早在1968年就于风洞实验室开展了弹性支撑刚性圆柱的涡激振动物理模型实验，成为了研究这一现象的经典。Williamson和Khalak[8-9]以及Govardhan等[10]于1996年开始，在水槽中进行了低质量比弹性支撑刚性柱体的涡激振动物理模型实验，同样十分经典，成为后续很多数值模拟的验证试验。随着数值模拟技术的飞速发展，学者们逐渐采用数值模拟方法对涡激振动问题展开研究，Lu 和Dalton[11]对雷诺数为13 000 情况下，仅在横流向发生运动的圆柱涡激振动问题进行了数值模拟，模型中的湍流方程采用大涡模拟的方法进行封闭。Dong 和Karniadakis[12]针对雷诺数为10 000的受迫振动圆柱受力问题，采用了直接数值模拟(Direct Numerical Simulation，DNS)的方法进行分析研究。郭晓玲等[13]研究了低雷诺数下串联双圆柱涡激振动机理，主要研究了双圆柱间干涉作用对涡激振动的影响。何长江和段忠东[14]，方平治和顾明[15]同样对涡激振动现象进行了数值模拟。Ge等[16]、Kang等[17]应用von der Pol方程模拟了悬浮隧道在水流作用的涡激振动问题，并研究了悬浮隧道锚链间距对隧道振动幅度以及锚链受力的影响。Su和Sun[18]应用尾流振荡模型同样模拟了悬浮隧道的涡激振动问题，发现涡激振动共振发生时，结构的运动轴向应力显著增加，但这些研究均是采用经验公式研究的悬浮隧道涡激振动问题，没有采用精确地计算流体力学(Computational Fluid Dynamic, CFD)模型对其模拟。还有其他国内外学者都进行过相关研究，但是其研究大多针对某一特定雷诺数的涡激振动问题，而并没有计算根据某一特定工程背景研究一系列雷诺数下的水流与结构物的耦合运动问题。

基于上述研究背景，本文通过应用有限元数值方法求解不可压缩粘性流体雷诺平均Navier-Stokes方程，结合ALE动网格方法，建立了高雷诺数下水流与结构物耦合的数值模型，通过精确地CFD数值模拟，研究了雷诺数从1 000到100 000这一范围内的水流与悬浮隧道的耦合运动问题，并选取某一特定雷诺数，研究不同浮重比对悬浮隧道在水流作用下振动的影响，为实际工程提供参考价值。

2 数学模型的建立

对于水下悬浮隧道而言，由于结构自身尺度较大，同时隧道所处位置通常位于峡湾，水流流速较快，使悬浮隧道周围的流动通常表现为湍流态。目前，对于湍流的模拟可以通过DNS或采用合适的湍流模型进行近似，本文采用湍流模型的方法进行模拟。与此同时，由于悬浮隧道结构长度远大于断面尺寸，因此我们可以近似为二维水流与结构物的流固耦合问题。二维模型通常会计算出较大的计算结果，但是仍然可以揭示自振频率与振动幅值和受力特性的关系，很多学者(Lu和Dalton[11]，Dong和Karniadakis[12])同样也采用二维模型来求解类似问题。

2.1 控制方程及湍流模型

二维不可压缩粘性流体的雷诺平均N-S方程作为流动基本控制方程在ALE观点下可以表示为[19-20]

(1)

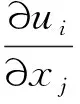
(2)

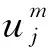
(3)

式中：υt为湍流粘性系数；k为湍动能；δij为Kronecker函数。

为了封闭湍流方程，本文采用了SST(Shear-Stress Transport)k-ω湍流模型[21-22]。所有参数均与Menter[21]以及Menter 等[22]相同，其所采用的参数已被广泛的接受和成功的应用，当模拟具有负压力梯度的边界层时，计算结果表现较好。SSTk-ω湍流模型的控制方程形式如下

(4)

(5)

其中

式中：Ω为涡量的绝对值；y*为到最近壁面的距离；F2和Dkω定义如下

其他参数通过F1求得

σk=F1σk1+(1-F1)σk2；σω=F1σω1+(1-F1)σω2；α=F1α1+(1-F1)α2；β=F1β1+(1-F1)β2

湍流模型用到的常数见表1所示。

表1 SST k-ω湍流模型中的参数Tab.1 Parameters of SST k-ω turbulent model

当计算得到流场和压力场后，通过对表面压力和粘性剪切力积分得到结构物所受到的流体作用力，进而得到结构物受到的拖曳力和升力，再对其无量纲化得到拖曳力系数CD和升力系数CL

(6)

(7)

2.2 悬浮隧道运动方程

对于悬浮隧道在水流作用下的振动问题，由于需要保证锚索结构始终在弹性范围内，因此尽管悬浮隧道管体会发生运动，将整个系统仍简化成质量-阻尼-弹簧系统。为了研究更有针对性，本文只考虑悬浮隧道在垂直水流方向(即横流向)的振动响应，其运动方程可表示为

(8)

式中：m，c，k分别为悬浮隧道的质量、阻尼以及刚度；Fy为悬浮隧道受到的垂直波浪力，由上一节的流动方程确定。

根据结构动力学关系，c/m=4πξfn，k/m=(2πfn)2，并定义悬浮隧道的质量与悬浮隧道排开水的质量之比m*=4m/πρD2，D为悬浮隧道外径，从而可得

(9)

式中：ζ为结构的阻尼比；fn为圆柱的固有频率；m*为质量比。

进一步定义如下的无因次关系式

(10)

式中：U为水流流速，同时根据升力系数的定义，Fy=0.5ρU2DCL，将式(9)进行整理，可以得到如下无因次结构运动方程

(11)

上式右端的升力系数前面已经给出表达式，即可通过上式计算圆截面悬浮隧道的动力响应。

2.3 计算模型及边界条件

应用圆柱来模拟悬浮隧道在水流作用下的运动，计算模型及边界条件如图1所示，将坐标原点设立于圆柱初始圆心，对计算模型进行无量纲化处理，圆柱直径D=1。在入口处指定无量纲的速度u=1，v=0；侧壁采用了对称边界条件∂u/∂y=0，v=0；出口处的速度边界条件为∂ui/∂t+c∂ui/∂xi=0，其中c为局部平均流速；圆柱表面的边界条件为不可滑移条件u=dx/dt，v=dy/dt。计算中，在出口处指定相对压力p=0，在其他边界采用∂p/∂n=0的压力边界条件，n为指出流体域的外法向单位矢量。在初始时刻，流场中速度及相对压力分布均设为零(即初始速度场满足连续方程)。

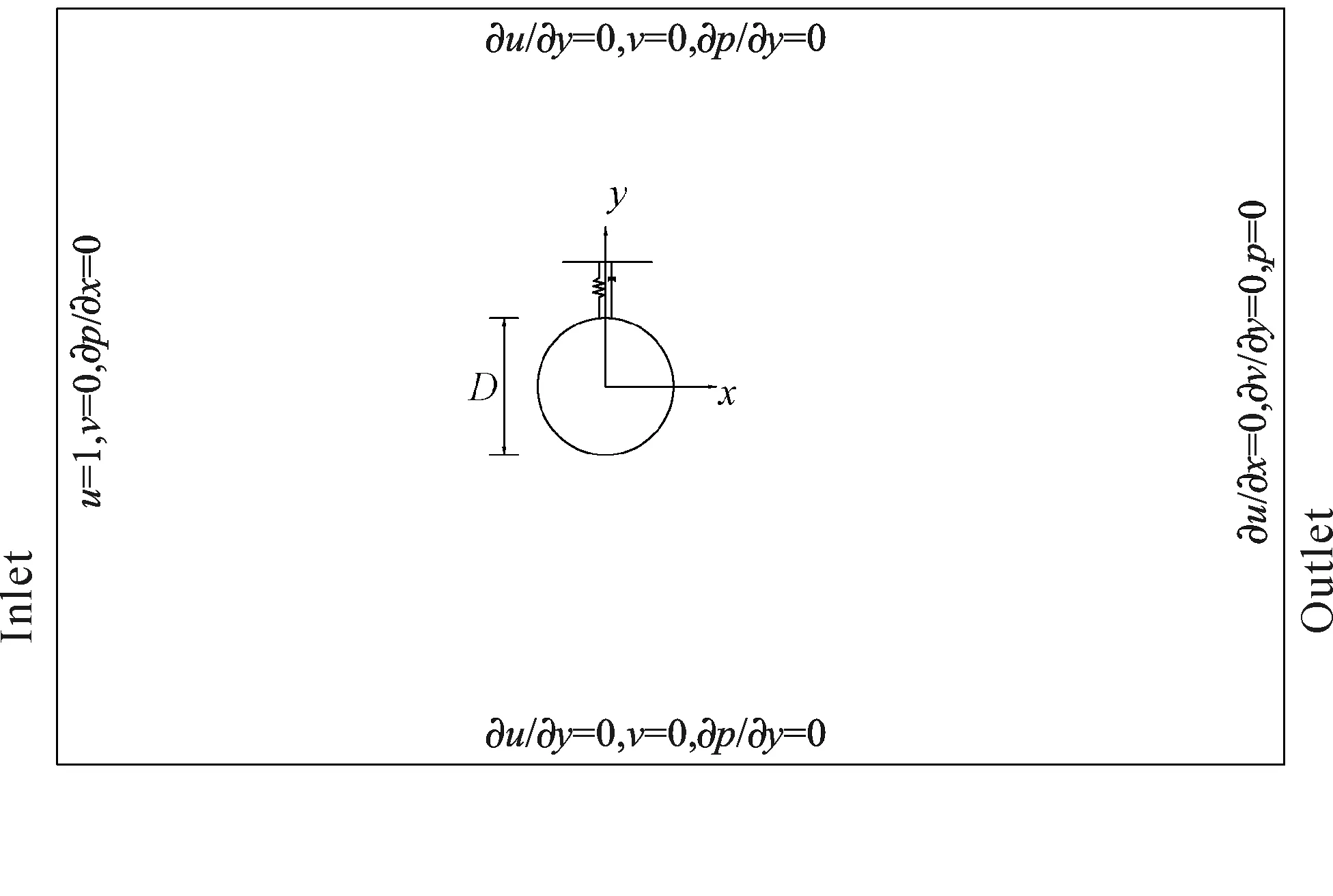
图1 计算域及边界示意图Fig.1 Sketch definition of computational domain and boundary conditions

3 数值离散及网格更新

本文对流扩散方程采用流线迎风有限元(SUPG-FEM)方法[23]进行求解。首先忽略压力项，只考虑对流和扩散项的中间速度；随后通过求解压力方程得到下一个计算时间步的压力；最后考虑压力梯度项修正流场。

针对结构运动方程的Newmark-β求解方法，对于时间步进，本文采用动态时间步长进行求解，表达式如下

(12)

式中：Sc为网格的面积；ue为网格中心点的流速；min表示在计算域内取最小值；Cs为安全系数，取Cs=0.2。而由于悬浮隧道在水流作用下会往复运动，针对该流固耦合问题采用ALE观点下的动网格方法对其进行数值模拟。本文将计算域内网格给予一定弹性模量，当网格运动时，其运动和变形可以通过求解线弹性动力学控制方程来获得[24]。应用该网格更新方法，使网格节点的位移较为均匀，大大提高了数值计算的稳定性；同时，还可以通过调整计算网格弹性模量来避免网格发生畸变。

4 数值模型验证

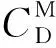
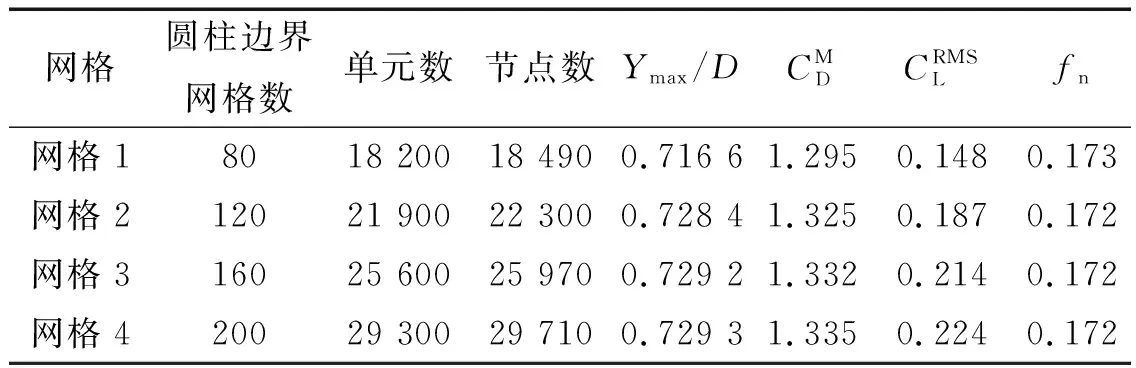
表2 网格收敛性验证结果Tab.2 Grid convergence verification results with different mesh solutions

应用计算收敛的网格，计算不同固有频率下的弹性支撑圆柱在水流作用下的振动，并同Khalak和Williamson[8]做过经典试验结果进行对比，计算参数与Khalak和Williamson试验中完全一致，雷诺数12 000，质量比m*=2.4，质量阻尼比m*ξ=0.013，计算结果如图2所示，图中横坐标表示不同的自振频率，纵坐标为垂直水流方向的振动幅值。从对比结果看，本文的模型所得到的幅值以及“锁定”区间和Khalak和Williamson的实验结果吻合良好。说明本文所建立的模型可以用于高雷诺数流固耦合问题的研究。

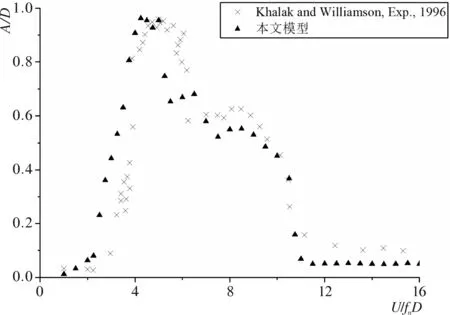
图2 弹性支撑圆柱计算结果同物理模型试验结果对比图Fig.2 Calculation result comparisons of cylinder with spring and damping between numerical model and experimental test

5 算例分析

5.1 不同雷诺数下悬浮隧道动力分析

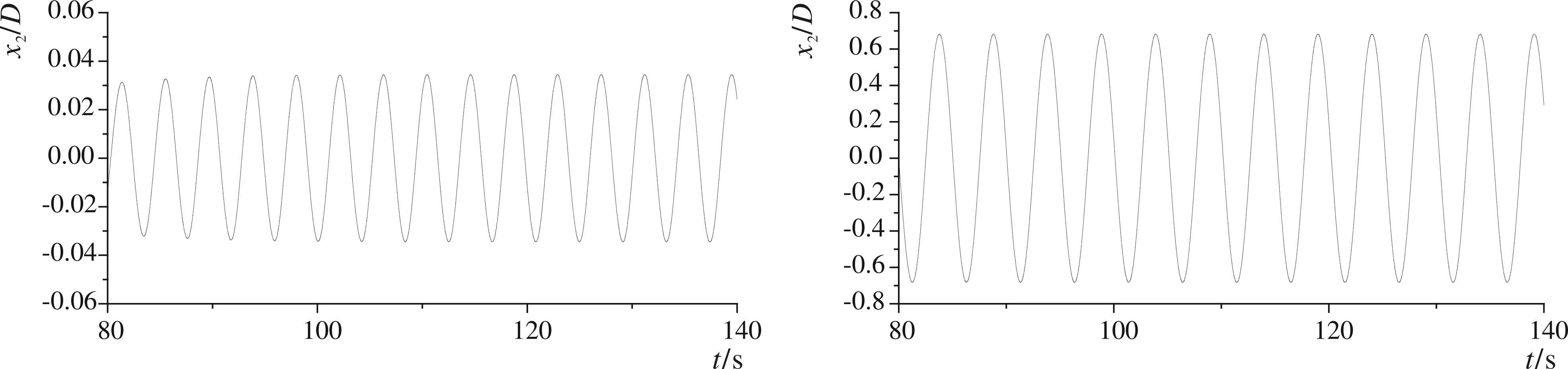
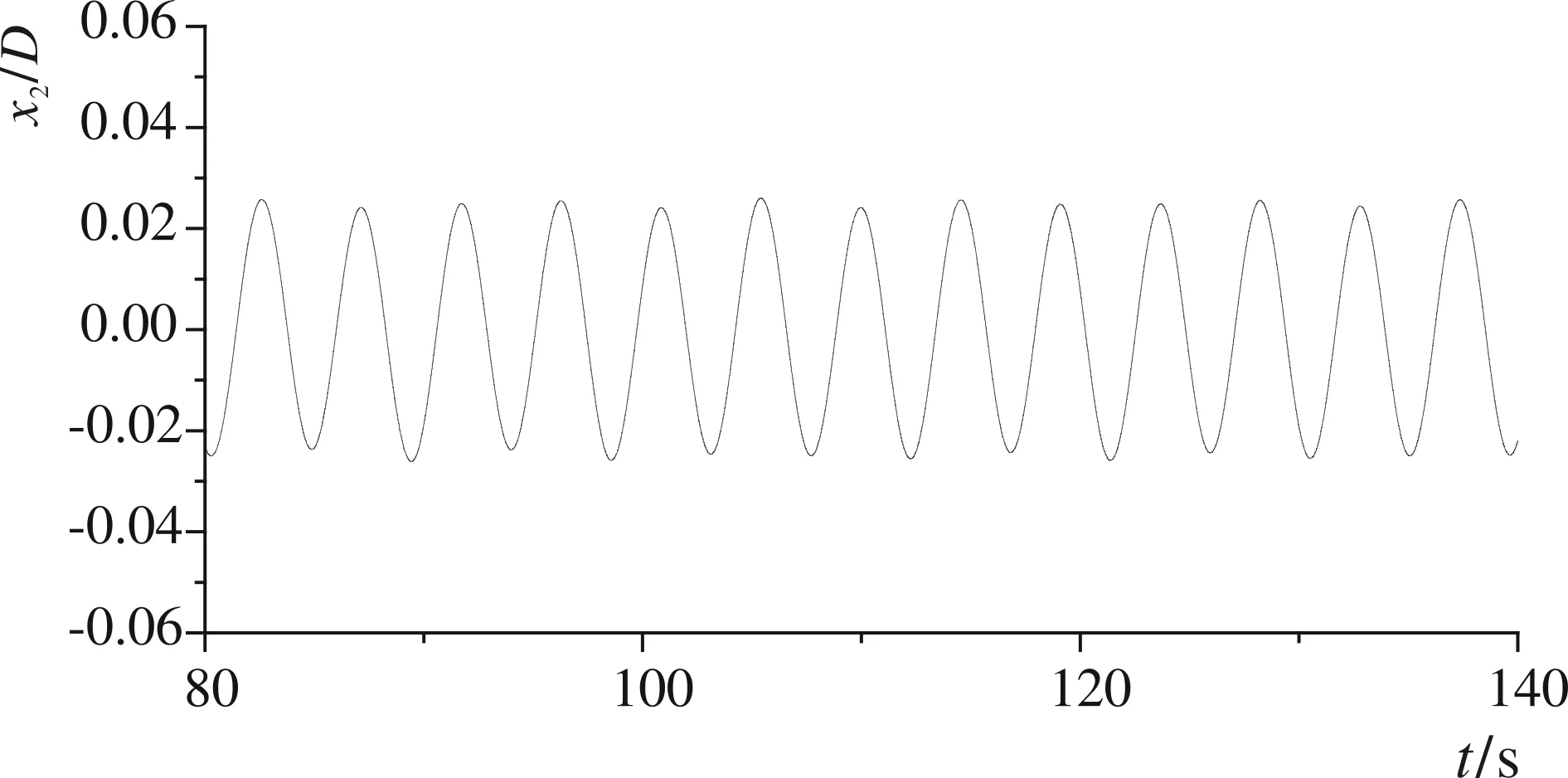
基于上述数值模型，本文计算了悬浮隧道在不同约束刚度，以及不同雷诺数下的运动情况。雷诺数从1 000计算到100 000，根据之前学者的描述，在这一区间内流体流动呈现湍流性质，尾流发生分离。在实际自然环境中，由于悬浮隧道尺度较大，在自然环境的水流作用下符合上述雷诺数。首先介绍雷诺数50 000，悬浮隧道质量比m*=2.5，系统的阻尼ξ=0.007、自振频率分别为 0.500 Hz、 0.200 Hz和0.083 Hz情况下的垂直水流方向的运动时间历程曲线，如图3所示。

3-c 自振频率fn=0.083 Hz(Re=50 000，m*=2.5，ζ=0.007)图3 不同自振频率情况下悬浮隧道运动时间历程曲线Fig.3 Time histories of SFT motion under different natural vibration frequencies

通过图3，可以发现当结构自振频率为0.5 Hz和0.083 Hz时，悬浮隧道垂直水流方向振动幅值较小，而当结构自振频率为0.2 Hz时，结构振动幅值较大。随后取振动幅度较大和较小的工况，分别对其流场进行分析，如图4和图5所示。

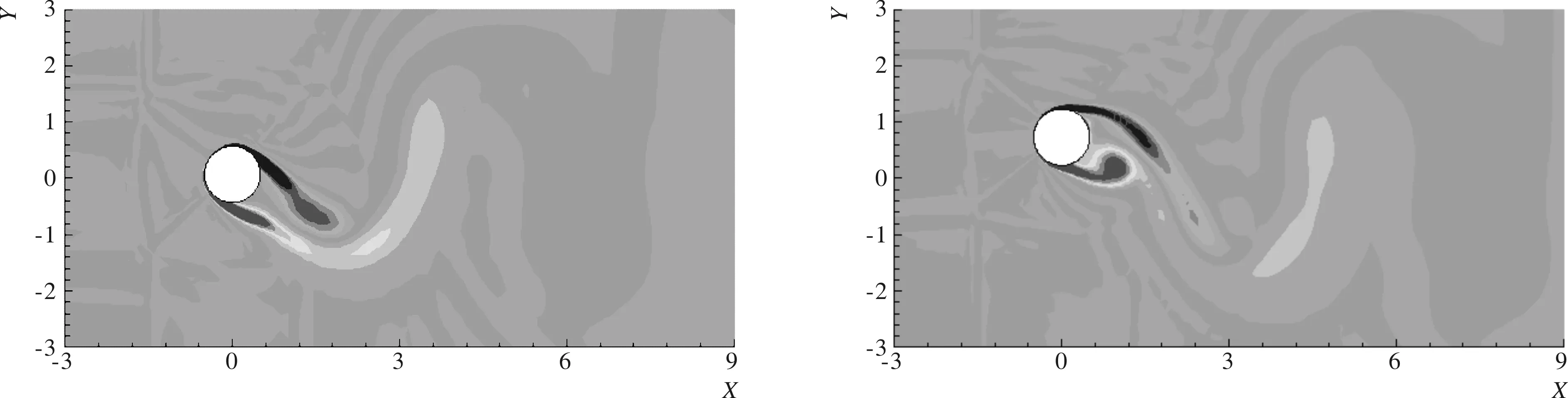
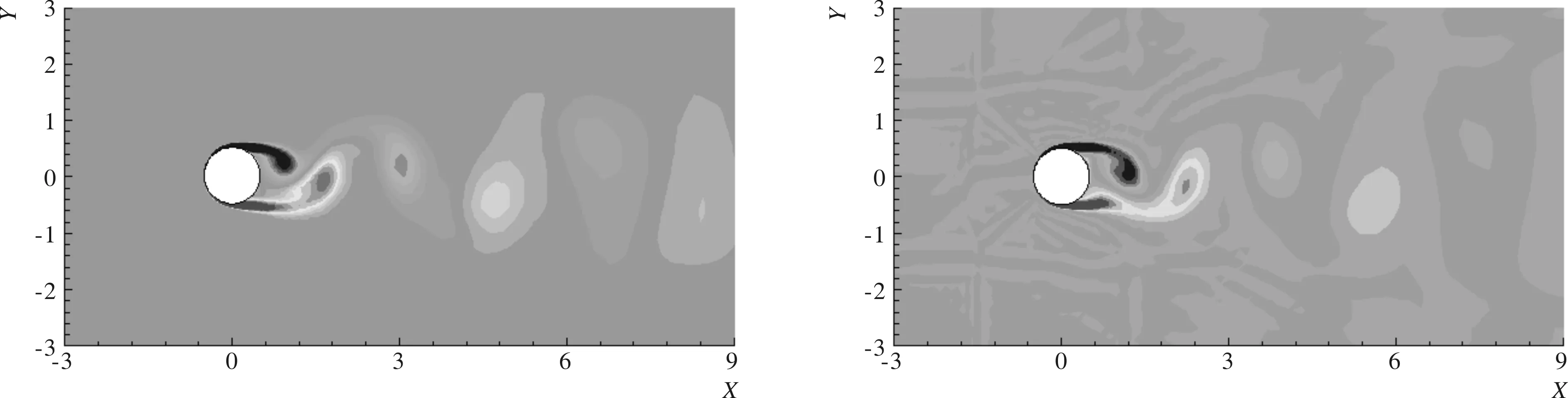
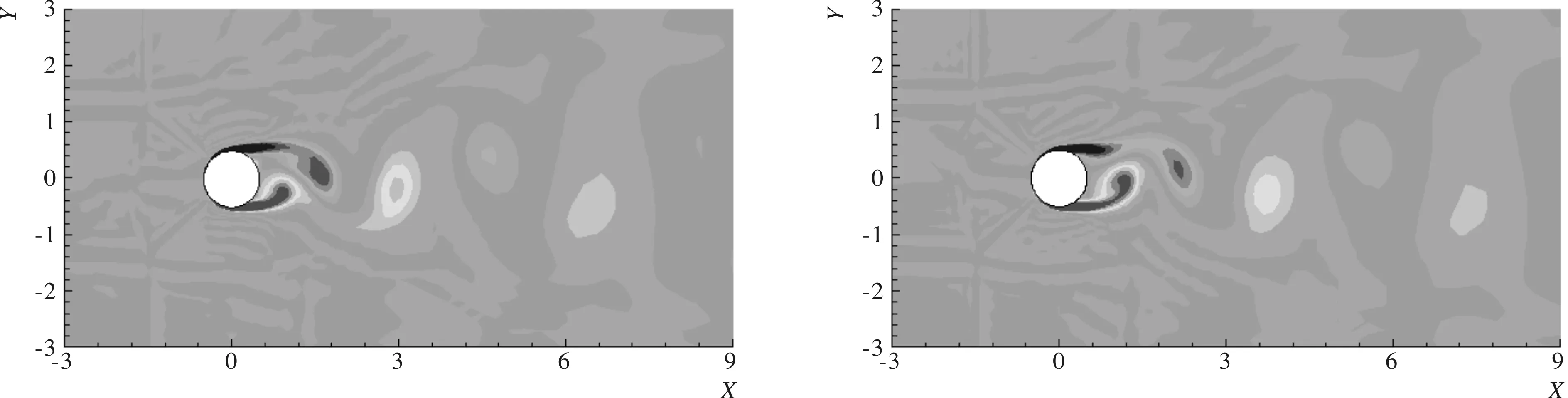
通过上述对比可以看出，当悬浮隧道系统自振频率为0.500 Hz和0.083 Hz时，此时涡脱落频率远离结构自振频率，悬浮隧道的涡激振动现象不明显，仅发生小幅值振动，其尾涡模式如图5所示，在同一振动周期内尾涡形态也很规律；但是当通过调整弹簧刚度使结构自振频率为0.200 Hz时，涡脱落频率与该频率较为接近，悬浮隧道在水流升力作用下发生了大幅度的VIV现象，悬浮隧道振动幅值达到了0.7 倍的悬浮隧道外径，其尾涡模式如图4所示，可以看出尾涡在剥离开后，有较长的“尾巴”，尾涡形态也没有规律。接下来我们比较该雷诺数下结构不同自振频率情况下水流与悬浮隧道的耦合作用，统计得到悬浮隧道在不同频率下的振动幅值，如图6所示。

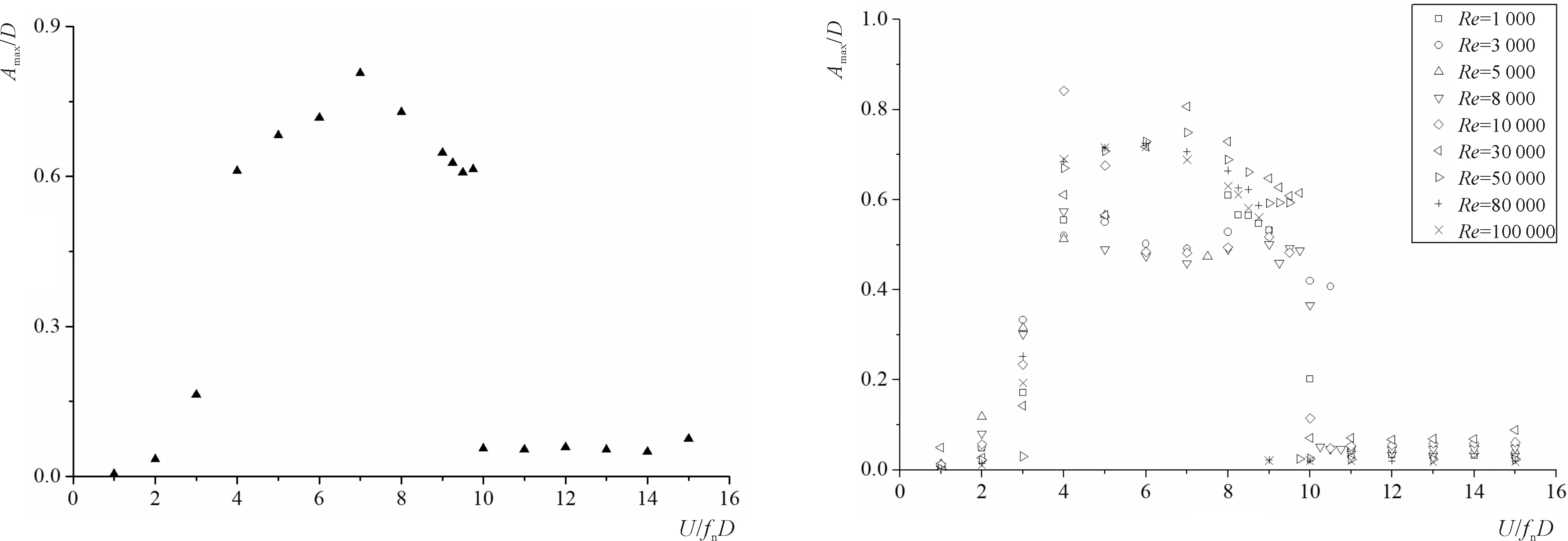
从计算结果可知，当悬浮隧道结构频率从0.1～0.25 Hz时，在水流作用下结构发生了“锁定”现象，而在其他频率时，结构运动幅值较小，随后比较相同质量比和阻尼情况下，不同雷诺数下的悬浮隧道涡激振动现象，计算结果如图7所示。从不同雷诺数下悬浮隧道的涡激振动结果来看，雷诺数对振动幅值影响较大。而对发生“锁定”的区间影响不大，无论雷诺数多大时，发生“锁定”的结构自振频率为0.12～0.25 Hz，因此悬浮隧道的自振频率要尽量避免在此频率范围内。

5.2 不同浮重比情况下悬浮隧道动力分析

浮重比对悬浮隧道影响很大，假设悬浮隧道水中尺寸不变，则其受到浮力不变，悬浮隧道浮重比越大，表明自身质量越轻，所需建造成本也就越小，但是带来的弊端就是锚索系统的预张力也就越大，因此为悬浮隧道找到一个合适的浮重比十分重要，接下来分析悬浮隧道浮重比(BWR)1.1、1.3、1.5、1.7和1.9五种情况，对应的质量比(m*)分别为2.1、2.3、2.5、2.7和2.9，现计算质量比为上述各值时其在水流下的动力响应和受力特征。计算中，随着悬浮隧道浮重比的变化，其受到的约束条件会相应改变，从而保证结构自振频率研究区间不变。再研究雷诺数Re=100 000，阻尼ζ=0.007的情况，计算结果如图8和图9。

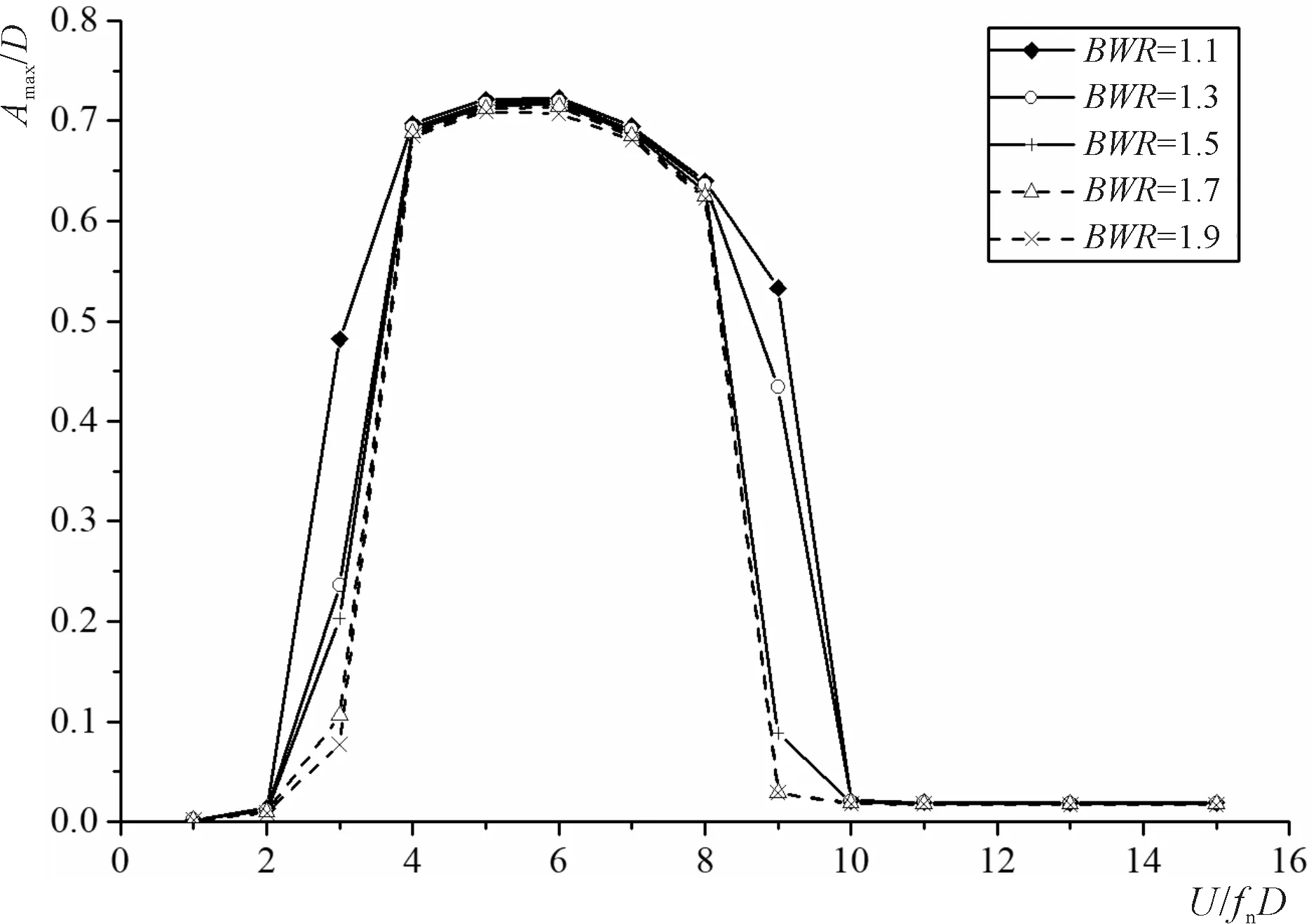
图8 不同浮重比情况下悬浮隧道在不同自振频率下的振动幅值(Re=100 000，ζ=0.007)Fig.8 Vibration amplitude of SFT versus natural frequency at different BWRs (Re=100 000, ζ=0.007)

图8为不同浮重比情况下悬浮隧道在不同自振频率下的振动幅值分析，从结果可以看出，浮重比对振动幅值影响不大，但是对引起“锁定”的频率区间有较大影响，当浮重比较小时，其发生“锁定”的区间较大，而当浮重比大于1.3后，发生“锁定”的结构自振频率区间区域一致，因此建议悬浮隧道的浮重比不要选择过小，这样可以更好地避免悬浮隧道发生涡激振动“锁定”现象。

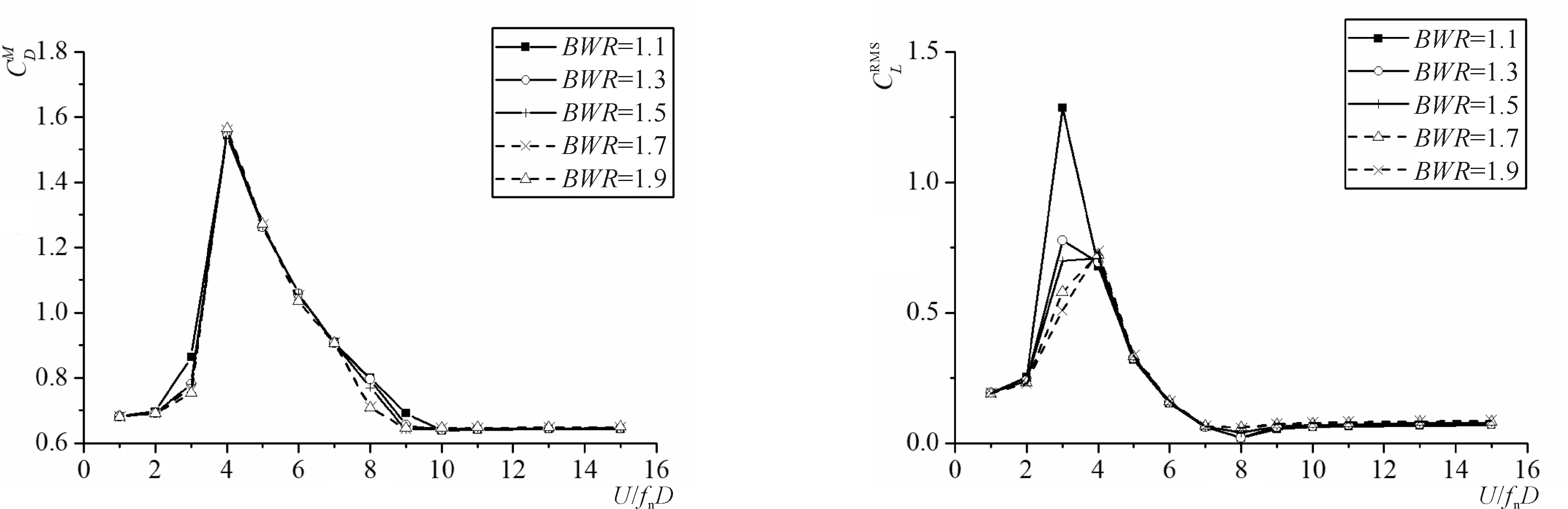
图9为不同浮重比情况下悬浮隧道在不同自振频率下的受力特性分析，从结果可以看出，浮重比对平均拖曳力系数和升力系数均方根影响不大，只是对个别频率下的升力系数有较大影响，建议在悬浮隧道设计时结构远离该自振频率。

6 结论

本文应用有限元数值方法求解不可压缩粘性流体雷诺平均Navier-Stokes方程，结合任意拉格朗日-欧拉(ALE)动网格方法，通过精确的CFD数值模拟，对不同雷诺数下悬浮隧道的涡激振动问题进行了研究，主要结论如下：

(1)通过网格敏感性分析证明数值模型的稳定性并找到了兼顾计算效率和精度的网格，随后通过模拟圆柱在高雷诺数下的涡激振动问题，与其他学者的实验结果对比，证明本文所建立的模型可以用于高雷诺数流固耦合问题的研究。

(2)通过悬浮隧道在水流作用下的涡激振动研究，分析了在不同结构自振频率下悬浮隧道的受力和运动情况，并研究了不同浮重比情况下悬浮隧道的受力和运动的结果。研究表明，雷诺数对发生“锁定”的区间影响不大；对于不同浮重比的悬浮隧道，浮重比对振动幅值和受力特性影响不大，仅对个别频率下的升力系数有较大影响，建议在悬浮隧道设计时结构远离该自振频率，但是对引起“锁定”的区间有一定影响，当浮重比较小时，其发生“锁定”的区间较大，因此建议设计时在保证锚索张力安全的情况下，尽量避免选取较小浮重比情况，既可以节省成本，又可以减小“锁定”区间。