离散点的导数算法

白东玉　赵康　张杰　杨文

摘  要：目前的微积分总体说来都是利用函数求微分和积分而来，最近几年发展起来的线性回归也需要先把数据训练成一个模型后才能对数据进行预测。文章介绍一种脱离数据到模型的方式，提出一种数据即模型的理论，这种模式仅采用最简单的数学计算得出导数斜率，从而获得离散数据中的导数，这种导数将突破微积分导数的概念，但这种导数具有和微积分导数同样的作用，即线性的变化趋势。相信这种方式在大数据的今天能得到广泛实践。

关键词：离散曲线;切线;数据科学;微分

中图分类号：O241.82      文献标识码：A 文章编号：2096-4706（2020）05-0035-03

Derivative Algorithm for Discrete Points

BAI Dongyu，ZHAO Kang，ZHANG Jie，YANG Wen

（Power China Kunming Engineering Corporation Limited，Kunming  650000，China）

Abstract：In general，the current calculus is the use of functions to differentiate and integrate，the development of linear regression in recent years also needs to train the data into a model before the data can be predicted. This paper introduces a way of breaking away from data to model，and puts forward a theory of data as model. This model only uses the simplest mathematical calculation to get derivative slope，so as to obtain derivative in discrete data. This derivative will break through the concept of calculus derivative，but this derivative has the same function as calculus derivative，that is，linear change trend. I believe that this way can be widely practiced in todays big data.

Keywords：discrete curve;tangent;data science;differential

0  引  言

一直以来，对于离散数据点曲线都存在一种认知，从总体上看，离散数据点可以构成一条直观的曲线，也认为它应该能够有类似导数的意义来确定某个位置的发展变化，但从微观上看，离散数据点是不连续的，且无法构成真正的线条，因此无法使用导数来研究其中的变化趋势。

目前对微积分的研究，大部分是利用函数作为研究对象，对具体的函数进行微分或积分处理，虽然这样的理论体系与函数的理论体系完美契合，但是对于那些不知道函数，只有一堆数据集合的情景却无法处理，特别是在当前大数据的时代里，没有像导数、积分等的数学术语来描述一个离散数据曲线的变化状态。而对于离散数据的研究更多的是以概率论与数理统计这样的方式来得出一个结论。

对离散数据的导数理论注定要打破传统导数理论的定义。如微积分中的导数定理为：设函数y=f（x）在点x0的某个邻域内有定义，当自变量x在x0处取得增量Δx（点x0+Δx仍在该邻域内）时，相应地，因变量取得增量Δy=f（x0+Δx）-f（x0）;如果Δy与Δx之比当Δx->0时的极限存在，那么称函数y=f（x）在点x0处可导，并称这个极限为函数y=f（x）在点x0处的导数，记为f ′（x）。而离散数据中的导数不仅不会利用极限定理，并且要将数据扩大到更大的邻域，用更多的邻域点参与计算得出切线。

1  概念理论

1.1  导数的意义

导数的几何意义在于表示函数曲线在点P0（x0，f（x0））处的切线的斜率（导数的几何意义是该函数曲線在这一点上的切线斜率），另外导数也表示曲线在某一点上的变化速率。本文主要探索导数的切线性质和表示变化速率的特征。

1.2  猜想

由于是离散数据，因此只能利用已有数据进行探索。无论从曲线的直观感受来看，还是以导数在函数中的定义来看，某一点x0的导数是由其位置及左区间、右区间决定的，但是如果在离散数据中仅以一两个点来做导数分析，相当于导数仅由少数几个点决定，必定会有巨大的波动。因此我们选取固定x区间的所有点位进行运算，至少要达到用肉眼能够判断得出的切线是否正确。

做此实验需要有一个相对正确的方法来确认这个方法的正确性，这里笔者使用sin函数+随机数的方法产生离散数据集。利用sin′（x）=cos（x）的导数公式来确认某一点的导数值。

由于本方法与之前函数求导的方法完全不同，因此也需要一个不同的计算方法。假设两个点a（x1，y1）和b（x2，y2），直线ab的斜率k1为（y2-y1）/（x2-x1），另外两个点c（x3，y3）和d（x4，y4），直线cd的斜率k2为（y4-y3）/（x4-x3），两条直线的平均斜率k3=tan（（arctan（k1）+arctan（k2））/2），当有n个斜率时，平均斜率为tan（1/n*arctan（ki）），也就是先求出n条线角度的平均值，再求这个平均角度的正切值。这个公式虽然从三角公式转化很难转化，但是我们使用到计算机程序实现时会变得十分方便。

制定好基本方法后，接下来就是具体操作。主要有以下步骤：

（1）生成规范数据样本。

（2）生成噪音数据，并将噪音数据融入规范数据样本。

（3）从噪音数据的头到尾依次选取切线计算点，针对每个计算点选取对应三种数据样本：切点位置区域样本;前置区域数据样本;后置区域数据样本。

（4）利用步骤（3）选取的三种数据样本，在求切线的时候，分别使用前置区域数据样本和切点位置区域样本、后置区域数据样本和切点位置区域样本计算斜率。关系点对应关系为[ai，bi]。

（5）利用两组斜率kn1和kn2。再利用kn1和kn2综合求出平均角度及其斜率。

（6）用图形化工具pyplot生成图形。

本文使用的x区间为[0，2π]，其中一共有10 000个点平均分布在x区间，设置一个波动值surge来确认随机波动数的波动幅度。每次选取的三个数据样本分别是100个，相当于x长度为2π/100。在样本生成结束后，从第150个点开始到9 850结束，选取这样的范围是为了满足前置、中置、后置的数据样本数量一致。

2  效果、调整与结论

2.1  初步尝试

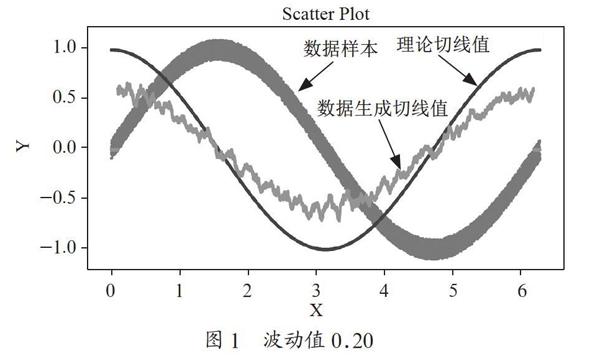
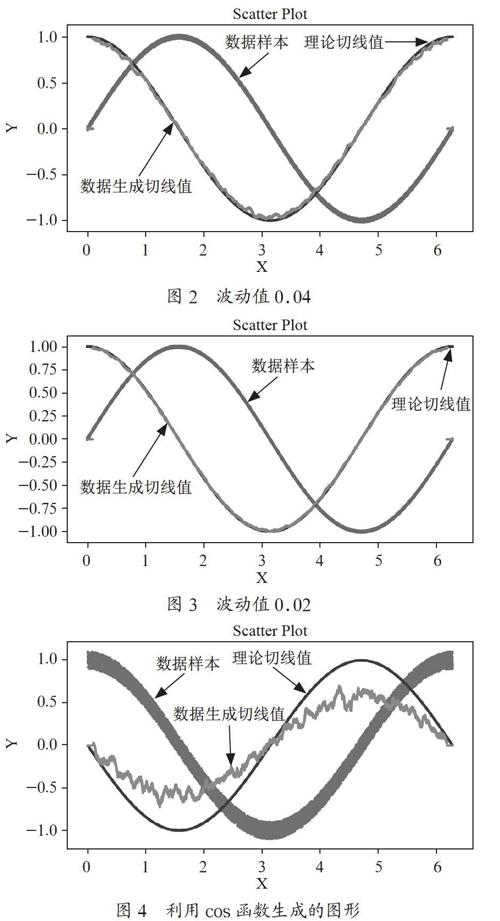
通过生成的结果发现，生成的切线趋势与原函数的切线趋势基本相同，但受波动值的影响较大，图1～图4分别展示了波动值为0.20、0.04、0.02的效果图，其中数据样本为数据点，理论切线值为sin函数的切线斜率，数据生成切线值为利用本论文的方法得出的斜率值，其中数据生成切线值线条两端的0点值为空缺占位值。

以下四幅图中，数据样本曲线是原函数值+噪音数据的结果曲线，当数据样本曲线较粗时，表示噪音数据的波動区间较大，如图1和图4所示;当数据样本曲线较细时，表示噪音数据的波动区间较小，如图2和图3所示。

理论切线值表示由原函数导数生成的切线值，图1、图2和图3的理论切线值由sin（x）的导数也就是cos（x）生成。数据生成切线值是由样本曲线中的数据利用1.2节所述方法生成的曲线。数据生成切线曲线和理论切线值差异越大，说明利用本方法计算的切线越不正确，如图1和图4所示，当数据生成切线值与理论切线值保持一致甚至看起来融合成一条线时，说明利用本方法计算的切线越正确，如图2和图3所示。

由上述方法，可能存在两个区域间的点间直线交叉的问题，假设前置区域有两点[a（1，2），b（2，3）]，切线区域有两点[c（3，1），d（4，5）]，斜率k（ad）和斜率k（bc）的平均斜率为0.333 00，斜率k（ac）和斜率k（bd）的平均斜率为0.162 27，因此笔者猜测，减少交叉直线可以减少切线波动。

2.2  新的猜想

为解决2.1节的猜测，在1.2节的步骤（3）和步骤（4）之间增加一个步骤，将步骤（3）选取的三个区域按照y值进行排序，且称为步骤（3.5）。这样步骤（4）用于计算的直线将不会存在交叉的关系。生成的效果图如图5所示。

由图5所示，可以看出增加步骤（3.5）后，数据生成切线比图1所示的数据生成切线能更好地与理论切线值融为一体，这说明改进后的方法能更好地计算切线值。

2.3  总结

由图1、图2、图3可见，波动值越小，切线斜率预测值与原函数的切线值越相近，两条线也越接近。由图4利用cos函数验证此方法的普遍性，说明此方法并非仅针对正弦函数适用。

由图5可见，计算前将区间数据按照y值排序后进行计算能够大幅提升切线的准确度。

3  结  论

本文依托Python进行具体实验，并得出图示，依托这些实验，也提出一种新的观点：数据集即函数。在这种概念下，寻找离散数据集导数的首要任务将不再是总结出原函数f（x），而是找到求导点位x0的当前区间、左区间及右区间，仅利用这些区间就求出点位x0的导数。此种方法也还有其他实验空间，如将三个数据集进行排序后再进行计算、其他数据集等。

本方法在如今的大数据时代，将离散的数据变得像函数一样处理具有重要意义，很多函数相关理论可以通过另一种形式来指导实践中的发展方向，可以帮助众多企业透过数据看趋势。由于本方法的数据取样仅是附近区间的数据而不是全部数据集，因此可以加快实时处理速度，对前置区间、当前区间、后置区间的区间长度的设置，能够针对自己的数据集设置不同区间，从而降低区间过大或过小带来的数据影响。

本方法能应用的领域很多，在计算机领域能够用于服务器网络速度的变化趋势、硬盘空间的增长趋势以及显卡性能分析等等，在基础建设工程中能够分析水位线的变化趋势、边桩沉降趋势、地质板块变动趋势等，在金融领域可以分析股票的变化趋势、全球经济变动趋势、消费者微观消费趋势等，在人体方面能够用于分析一个人的体能变化趋势、饮食对体力的影响趋势、心跳趋势等。

参考文献：

[1] 同济大学数学系.高等数学：第7版 [M].北京：高等教育出版社，2014.

[2] 盛骤，谢式千，潘承毅.概率论与数理统计：浙大·第4版 [M].北京：高等教育出版社，2012.

[3] 唐亘.精通数据科学：从线性回归到深度学习 [M].北京：人民邮电出版社，2018.

作者简介：白东玉（1989.08-），男，汉族，云南文山人，助理工程师，本科，研究方向：数据分析。