一种基于关联规则的MLKNN多标签分类算法*

杨岚雁，靳 敏，张迎春，张 珣

(1.北京工商大学计算机与信息工程学院，北京 100048；2.北京工商大学信息网络中心，北京 100048)

1 引言

分类算法是机器学习方法的重要内容，能够有效解决应用领域数据的分类问题。传统分类算法主要解决的是单标签分类问题，然而随着信息技术的发展，多标签分类已经成为分类问题中不可或缺的一部分，在现实生活中多标签分类[1,2]问题的应用也变得越来越广泛，例如，场景分类、生物信息学、多媒体自动标记与数据挖掘等领域的应用。在多标签分类问题中，标签之间存在着一定的关联性，若忽略标签之间的关系，则会损失标签间的关联信息。故本文采用关联规则[3,4]算法挖掘标签之间的相关性，将标签之间的关联规则应用到多标签分类算法中进行改进，这样既不改变样本分布，又能避免标记增多时的“维数灾难”问题。

在多标签研究中，主要有2类多标签分类算法：问题转化法和算法转化法。问题转化法是将多标签分类问题分解为多个单标签分类问题，再利用传统的单标签分类方法进行分类，简单易行，但这样就忽略了多标签数据集的所有特性。如复制转化CO(COpy transformation)[5]法通过直接复制样本将多标签的问题转换成多类问题，简单易行，但是完全把多标签问题当成单标签问题进行求解，忽略了多标签数据集的所有特性。二元关联BR(Binary Relevance)[6]算法通过将多标签学习问题转化为每个标签独立的二元分类问题，并为每个标签构建一个独立的分类器，每个分类器使用全部训练样本进行学习，这种算法忽略了标签和标签之间的相关性，分类准确率有待提升。标签幂集LP(Label Power-set)算法考虑了标签之间的相关性，通过二进制编码将每个样本可能拥有的标签合并成为一个新的标签，但是该算法会导致融合后的标签呈指数级增长，样本不足不具备良好的泛化性。多标签随机游走RAKEL(RAndom K-labELsets)算法[7]是由Tsoumakas等人提出的一种随机选择多个标签集合的子集建立LP分类器的多标签分类算法，为了弥补LP算法的短处，其在原始标签集中随机选用部分标签子集来训练每个分类器。但是，由于RAKEL算法是随机构造标签空间，并未充分考虑到样本和多个标签之间的相关性，从而造成分类精度不高。

算法转化法是通过对传统的分类方法进行改进，使其能适用于多标签数据的分类。该类算法主要有AdaBoost算法[8,9]、C4.5算法[10]、多标签K近邻算法MLKNN(Multi-Label K-Nearest Neighbor)[11]和反向传播多标签学习BPMLL(Back-Propagation for Multi-Label Learning)算法[12]等。AdaBoost算法是由Schapire等人[8]提出的一种基于迭代的多标签文本分类算法，其核心思想是针对同一个训练集训练不同的分类器(弱分类器)，然后把这些弱分类器集合起来，构成一个更强的最终分类器(强分类器)。这类算法可以根据弱分类器的反馈，自适应地调整假定的错误率，执行的效率高，但在训练过程中会使得难于分类样本的权值呈指数增长，导致算法易受噪声干扰。此外，这类算法依赖于弱分类器，而弱分类器的训练时间往往很长。C4.5算法是由Quinlan[9]提出的用于产生决策树的算法，该算法产生的分类规则易于理解且准确率较高，但该算法在构造树的过程中，需要对数据集进行多次顺序扫描和排序，因而导致算法的效率较低。MLKNN算法是Zhang[10]提出的一种基于KNN的多标签分类算法。该算法的基本原理是通过KNN算法寻找和样本最近的k个样本，然后对这k个最近邻样本的标签集进行统计分析，计算出这些近邻样本包含各个标签的概率，利用最大后验概率方法来确定当前未知样本的标签集。此算法易于理解且容易实现，但并未考虑标签之间的相关性。BPMLL算法[11]是在流行的反向传播算法中引入了一个考虑排序损失的新误差函数，该算法考虑标签两两之间的相关性对泛化性能有一定的帮助，但是当现实中数据之间的关联性超过二阶时，此类处理方法就会受到一定的影响。

为克服现有技术的不足，本文提出一种基于关联规则的MLKNN多标签分类算法FP-MLKNN。该算法针对多标签数据考虑标签与标签之间的相关性，采用关联规则算法挖掘标签之间的高阶相关性，用标签之间的关联规则改进MLKNN算法，并通过了算法的有效性检验。实验结果表明，本文所提出的基于关联规则的MLKNN多标签分类算法极大地提高了多标签数据分类的准确性。

2 相关介绍

2.1 多标签问题的定义

令X={x1,x2,…,xn}表示样本空间，L={l1,l2,…,ln}表示标签集合，Y={yx1,yx2,…,yxn}表示标签空间，对于L中的任意一项li(1≤i≤q)，都有li∈{0,1}，li取0时表示该标签为无相关标签，li取1时表示该标签为相关标签。给定训练集D={(xi,li)|1≤i≤n,xi∈X,li∈L}，多标签学习的目标是从给定训练集D中训练得到一个多标签分类器h:X→2L，通过训练得到的多标签分类器来预测未知样本所包含的标签集合。但是，在大多数情况下，多标签分类系统的输出对应于一个实值函数f:X×L→R，f(xi,li)为样本xi包含标签li的置信度。当给定一个样本数据xi，若样本xi的标签集yxi中包含标签li，则f(xi,li)的值较大；反之，f(xi,li)的值较小。多标签分类还可以由此函数得到：h(xi)={li|f(xi,li)>t(xi),li∈L}，其中t:X→R作为阈值函数，用来决定是否应该将数据xi归属到标签li中。

2.2 关联规则

基于关联规则的分类是针对数据集挖掘频繁模式建立分类器，实现对未知样本分类的方法。相关定义如下：给定数据集D，|D|为数据集样本总数，I={i1,i2,…,im}为所有项的集合，is和it是I中任意项集，数据集D中的关联规则表示为蕴含式is⟹it，且is⊂I，it⊂I，is∩it≠∅，关联规则的强度可由支持度和置信度来度量，支持度表示规则的频度，置信度表示规则的强度。

规则is⟹it在D中的支持度是指同时包含is和it的样本数与数据集样本总数之比，记作：

Support(is⟹it)=P(is∩it)=

Freq(is∩it)/|D|

(1)

其中，Freq(is∩it)表示同时包含is和it的样本数。

规则is⟹it在D中的置信度是指同时包含is和it的样本数与包含is的样本数之比，记作：

Confidence(is⟹it)=P(is|it)=

Freq(is∩it)/Freq(is)

(2)

其中，Freq(is)表示包含is的样本数。

关联规则挖掘就是在数据集D中找出支持度和置信度分别大于用户给定的最小支持度(Minsup)和最小置信度 (Minconf)的关联规则。当规则的置信度和支持度分别大于Minsup和Minconf时，认为该关联规则是有效的，称为强关联规则。关联规则挖掘算法主要有Apriori算法和FP-Growth算法[12]，Apriori算法效率相对较低且存在冗余模式，因此本文采用FP-Growth进行关联规则的挖掘，进而得到多个标签之间的相关性。FP-Growth算法只需要对数据库进行2次扫描，通过FP-tree[14]数据结构对原始数据进行压缩。

2.3 求解策略

目前，基于标签相关性的求解策略主要有3类：

(1)一阶策略：逐一考察单个标签，将多标签分类问题转化为多个独立的二分类问题。此类策略将标签之间的关系看作是相互独立的，彼此之间没有任何影响，需要针对每一个类别或者一组标签训练一个分类器。虽然这类策略实现简单，但是没有考虑标签之间的相关性，在标签个数较多的时候需要训练很多分类器，分类效率和准确率可能不是最优。

(2)二阶策略：考察标签两两之间的相关性(例如相关标签与无关标签之间的排序关系等)，此策略在一定程度上考虑了标签之间的相关性，对泛化性能有一定的帮助，但是当现实中数据之间的关联性超过二阶时，此类策略就会受到一定的影响，且在标签规模较大时需要考虑的两两标签的相关性将变得非常多。

(3)高阶策略：此类策略考虑了标签之间的高阶相关性，对每一类标签，需要考虑标签集中其他标签对其的影响。该类策略可以较好地反映真实世界问题的标签相关性，并且相对于以上2类标签相关性建模方式有更强的建模能力。关联规则可以发现标签之间的高阶相关性，本文基于标签之间的关联规则对现有的多标签分类算法MLKNN进行优化。

3 基于关联规则的MLKNN多标签分类算法FP-MLKNN

3.1 基于FP-Growth算法的频繁项集挖掘

FP-Growth算法是通过构造一个树结构来压缩数据记录，使得挖掘频繁项集只需要扫描2次数据库，该算法不需要生成候选集合，效率比较高。

3.1.1 多标签转化为项集

对多标签数据集中的标签进行处理，将其转化为关联规则中的项集，以便后续的挖掘应用。多标签数据集中样本的标签是形如F=[1,0,0,1,0,1,…]的形式。数组F的长度表示数据集标签的数量，F[i]表示第i个标签，当F[i]为0时，表示样本不包含该标签；当F[i]为1时，表示样本包含该标签。本文首先对数据集标签进行处理，将其转化为项集的形式。如F1=[0,1,1,0,0,1]转化成[1,2,5]的形式，表示该样本拥有的标签下标为1,2,5。本文对多标签数据进行样本标签的转化(即把数据集中的样本用样本所包含标签的下标来表示)，便于关联规则的挖据。

3.1.2 生成关联规则

对多标签数据集中的标签进行处理，采用FP-Growth对多标签数据集标签的项集进行频繁项集的挖掘，根据频繁项集生成多标签数据标签之间的关联规则，然后对规则进行筛选。FP-Growth算法主要分为2部分：构建FP-tree以及利用FP-tree进行频繁项集的挖掘，算法过程如下所示：

(1)对转化后的数据样本标签进行扫描(第1次扫描)，得到所有频繁项集的计数以及对应的支持度，然后删除支持度低于阈值的项，将频繁项集放入项头表，并按照支持度进行降序排列。

(2)对数据进行扫描(第2次扫描)，将读到的原始数据删除非频繁项集，并按照支持度降序排列。

(3)读取排序后的数据构建FP-tree，构建时按照排序号的顺序插入FP-tree中。排序靠前的节点是祖先节点，靠后的节点是子孙节点。如果有公用的祖先节点，则对应的公用祖先节点加1。插入后，如果有新的节点出现，则项头表对应的节点会通过节点链表连接上新节点。当所有的数据都插入到FP-tree中后，FP-tree建立完成。

(4)从项头表的底部项依次向上找到项头表项对应的条件模式基，从条件模式基递归挖掘得到项头表项的频繁项集。

(5)如果没有限制频繁项集的项数，则返回步骤(4)得到所有的频繁项集，否则只返回满足项数要求的频繁项集。

3.2 基于MLKNN算法求样本的特征置信度

利用MLKNN算法计算出每个样本根据特征得到的拥有标签的概率，即特征置信度。MLKNN算法是通过KNN算法寻找和样本最近的k个样本，统计这k个样本中每个类别的个数，再通过最大后验概率计算样本包含每个标签的概率。设训练集X={x1,x2,…,xn}，标签集Y={yx1,yx2,…,yxn}。

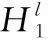
基于贝叶斯概率公式的MLKNN算法的分类函数如式(3)所示，通过式(3)来确定样本xi是否包含标签l。只需看b∈{0,1}中哪种情况使得式(3)的值最大，若b=1时最大，则xi包含标签l，yxi(l)=1；若b= 0时最大，则xi不包含标签l，yxi(l)=0。

(3)

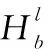
(4)

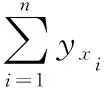
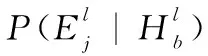
(5)

(6)

其中，j代表测试样本xi的k近邻中包含标签l的个数；c[j]代表在所有训练样本中，其k近邻有j个含l标签，且其自身也有l标签的样本个数。c′[j]代表在所有训练样本中，其k近邻有j个含l标签，且其自身不含l标签的样本个数。

本文通过式(7)计算得到样本xi包含标签l的概率：

(7)

基于MLKNN算法求样本的特征置信度过程描述如下：

%计算先验概率

forl∈ydo

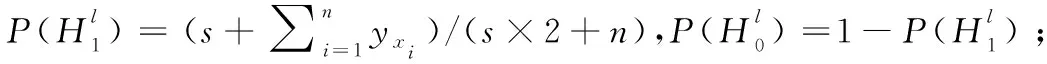
end

%计算后验概率

IdentifyN(xi)，i∈{1,2,…,n};/*N(xi)为样本xi的近邻集合*/

forl∈ydo

forj∈{0,1…,k}do

c[j]=0;c′[j]=0;/*c[j]和c′[j]初始化均为0，用来存储k个近邻中分别包含和不包含标签l的个数*/

end

fori∈{1,2,…,n}do

δ=Cxi(l);

if(yxi(l)==1)then

c[δ]=c[δ]+1;

elsec′[δ]=c′[δ]+1;

end

forj∈{0,1…,k}do

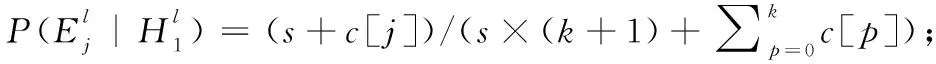
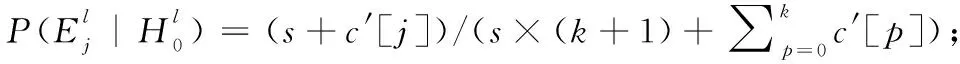
%计算训练样本的特征置信度P(l)

end

forl∈ydo

j=∑a∈N(t)ya(l);/*j表示测试样本t的k个近邻中包含标签l的个数*/

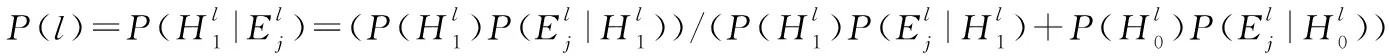
end

3.3 FP-MLKNN算法流程

本文提出了一种基于关联规则的MLKNN多标签分类算法，采用关联规则算法挖掘标签之间的高阶相关性，并将其融入到MLKNN中进行改进。算法流程如下所示：

步骤1利用MLKNN算法计算出每个样本根据特征得到的拥有标签的概率，即样本的特征置信度。

(8)

其中，Confm(li)表示样本拥有标签的li预测概率。

步骤2采用FP-Growth算法进行关联规则的挖掘生成频繁项集，通过调节支持度与置信度得到一系列强关联规则Confa。

(9)

其中，Confa是求所有A⟹li的置信度，{A，li}组成的所有集合为基于FP-Growth算法挖掘生成的频繁项集。

步骤3通过步骤1将预测概率大于0.5的标签筛选出来组成集合Lt，然后从步骤2中筛选出集合A属于集合Lt子集的最大Confa，即max(Confsa)，其中，Confsa为Confa中的元素。再计算样本最终拥有某标签的概率。

P(li)=w*Confm+(1-w)*max(Confsa)

(10)

其中，P(li)为样本最终拥有某标签的概率，w为标签相关性的影响程度。

基于关联规则的MLKNN多标签分类算法FP-MLKNN如算法1所示：

算法1FP-MLKNN算法

输入：训练数据集X，测试集T，近邻数k，标签相关性的影响程度w。

输出：测试集T对应的标签集Yt。

标签集合L={l1,l2,l3,…,lq}

fori=1,2,3,…,qdo

根据式(8)计算得到测试集T的特征置信度。

end

由关联规则算法，通过调节支持度(support)与置信度(confidence)得到一系列强关联规则Confa;

fori=1,2,3,…,q)do

将T对应的标签li的特征置信度大于0.5的作为转化为集合Lt

end

forConfsainConfa do

ifConfsa中的A是Lt的子集then

Confsa=p(li|A={l1∪l2∪…∪ln})

end

fori=1,2,3,…,qdo

由式(10)计算标签概率P(li);

ifP(li)>0.5then

li∈Yt

end

4 实验与分析

4.1 实验数据

本文在yeast、emotions和enron 3个不同领域的数据集上进行实验，数据集的具体信息如表1所示。

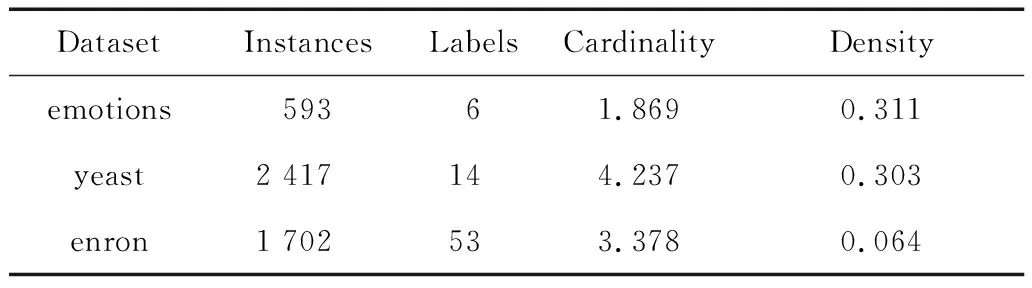
Table 1 Experimental datasets

其中，Cardinality和Density分别表示标签的基数和标签的密度，标签的基数为样本的平均标签个数，标签的密度为标签的基数与标签总数的比值。

本文采用十折交叉验证法，即将数据集分成10份，轮流将其中9份作为训练数据，1份作为测试数据进行验证。本文进行了10次十折交叉验证，并求其平均值作为最终对模型精度的估计。

4.2 评价指标

实验采用Hamming loss、One-error、Coverage、Ranking loss和Average precision多标签分类算法评价指标对FP-MLKNN多标签分类算法进行有效性验证。

Hamming loss指标考察样本在单个标签上的错误分类的情况，即属于该样本的标签没有出现在该样本的标签集合中，不属于该样本的标签出现在该样本的标签集合中。该指标越小，被错分类的情况越少，算法性能越好，最优值为hloss(h)s=0。

(11)

其中，h为分类器，Δ表示2个集合之间的对称差(异或)，s表示测试样本个数，q表示所有标签个数，h(xi)表示样本xi预测标签的集合，Yi表示测试样本xi实际标签的集合。

One-error指标用来评估在输出结果中排序第一的标签并不属于实际标签集的概率。该指标取值越小算法性能越优，最优值为one-errors(f)=0。

(12)

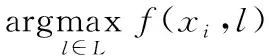
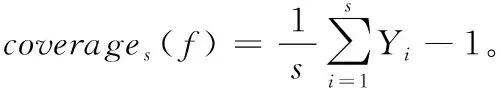
(13)

Ranking loss指标表示在样本拥有的标签集合排序序列中出现错误排序的情况，即无关标签在排序序列中位于相关标签之前。该值越小算法性能越优，最优值为rlosss(f)=0。

(14)

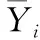
Average precision指标表示在样本拥有的标签集合排序序列中，排在相关标签集的标签前面，且属于相关标签集的概率。该指标越大算法性能越优，最优值为avgprecs(f)=1。

rankf(xi,l),l′∈Yi|)/rankf(xi,l)

(15)

其中，rankf(xi,l)为实值函数f(xi,l)对应的排序函数,f(xi,l)表示标签l的预测概率。

4.3 实验结果及分析

采用改进后的算法在yeast、emotions和enron 3个数据集上进行实验。首先，选取合适的支持度与置信度筛选出每个数据集合适的强关联规则；然后调整相关性的影响程度w进行验证。表2～表4是近邻数k为3,6和10时原始算法与改进算法的实验结果比较；表5是近邻数k为10时改进算法与MLKNN、AdaBoostMH、BPMLL这3种算法的实验对比。符号↓表示该指标越小性能越好，↑表示该指标越大性能越好，加粗表示在同一行中对应参数下最好的结果。

从表2～表4中可以看出，近邻数越大，分类效果越好，这是因为k值越大，近邻中包含的信息越多，从而能更好地利用标签之间的相关性使得分类结果更加准确，但是较大的k值需要找到更多的近邻，从而增加了算法的复杂度。而对于参数w(0≤w≤1)，在取值变化过程中,对于包含不同标签集的数据集而言，w并不是取值越大越好，对于不同的数据集，使得算法性能最好的w值是不一样的。这是因为不同的数据集中样本的个数以及标签集的大小是不同的，其对应标签的关联规则也是不同的。因此，要选择合适的w进行算法的改进。

从表中的实验结果可以看出，选择合适的w改进的算法相对于原始算法MLKNN性能有所提升。这是由于标签之间是存在相关性的，MLKNN算法没有考虑标签之间的相关性，因此本文采用关联规则算法挖掘标签之间的相关性，并将标签之间的关联规则应用到MLKNN算法改进中，使得最后的分类效果所有提升。改进算法相对原始算法复杂度也有所增加，在样本数为N、标签数为M的数据集中，寻找某个样本的k近邻，需要计算出其与所有样本的距离，时间复杂度为O(N)，然后对这些距离进行排序，使用最优排序算法的时间复杂度为O(NlogN)，所以MLKNN算法训练过程的时间复杂度为O(N2logN)。本文算法在MLKNN算法的基础上增加了对标签之间相关性的挖掘，相对MLKNN算法增加了关联规则算法的复杂度。使用FP-Growth算法进行关联规则的挖掘，在第1次遍历数据库时，时间复杂度为O(N)，第2次遍历数据库时，完成对FP-tree的构建，时间复杂度为O(NlogN)，挖掘频繁模式时，对所有项的条件模式进行递归查找，时间复杂度为O(MlogM)。综上所述，关联规则算法复杂度为O(N)+O(NlogN)+O(MlogM)。

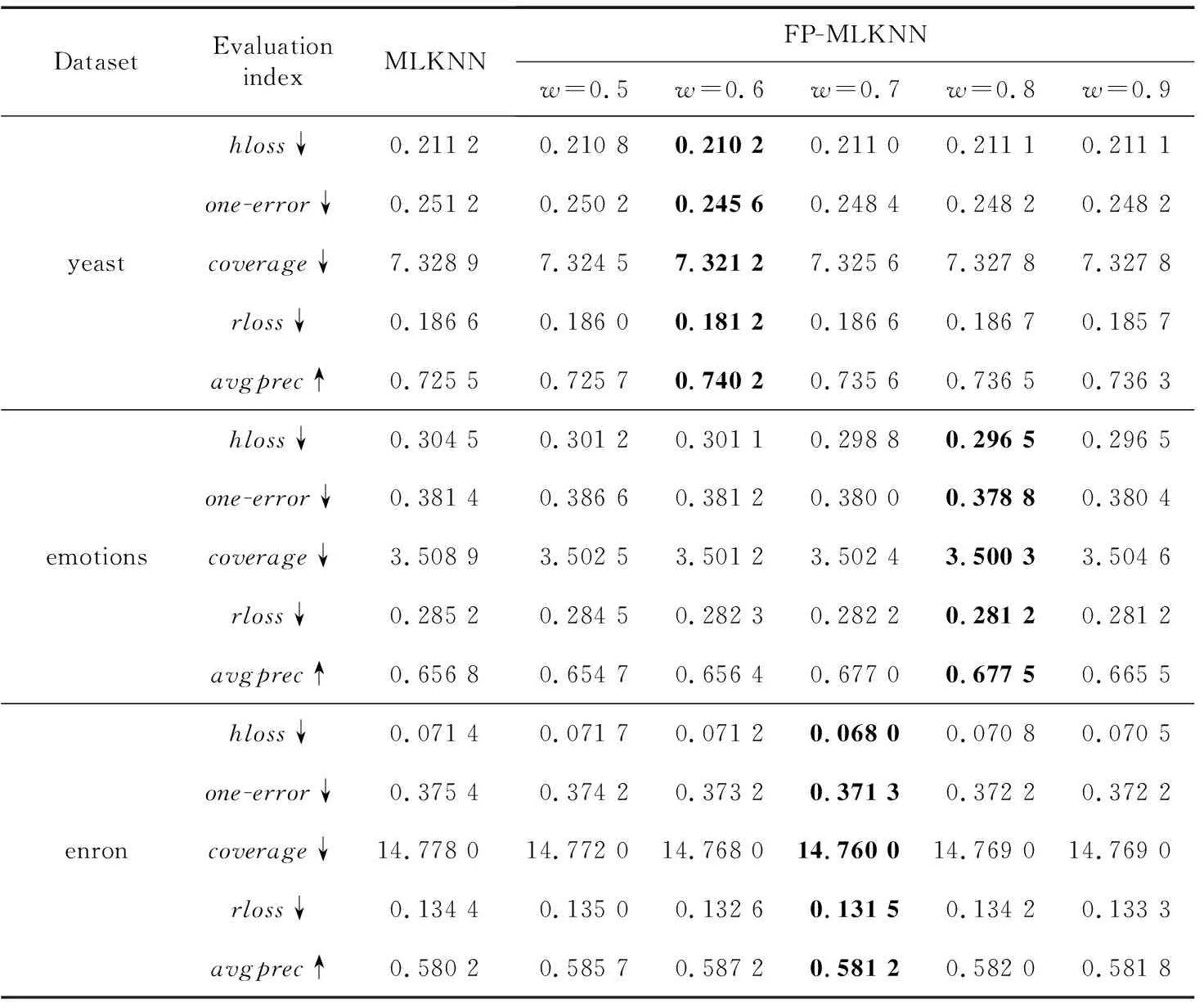
Table 2 Comparison of experimental results between the original algorithmand the improved algorithm with differentwvalues whenk=3

Table 3 Comparison of experimental results between the original algorithmand the improved algorithm with different w values whenk=6

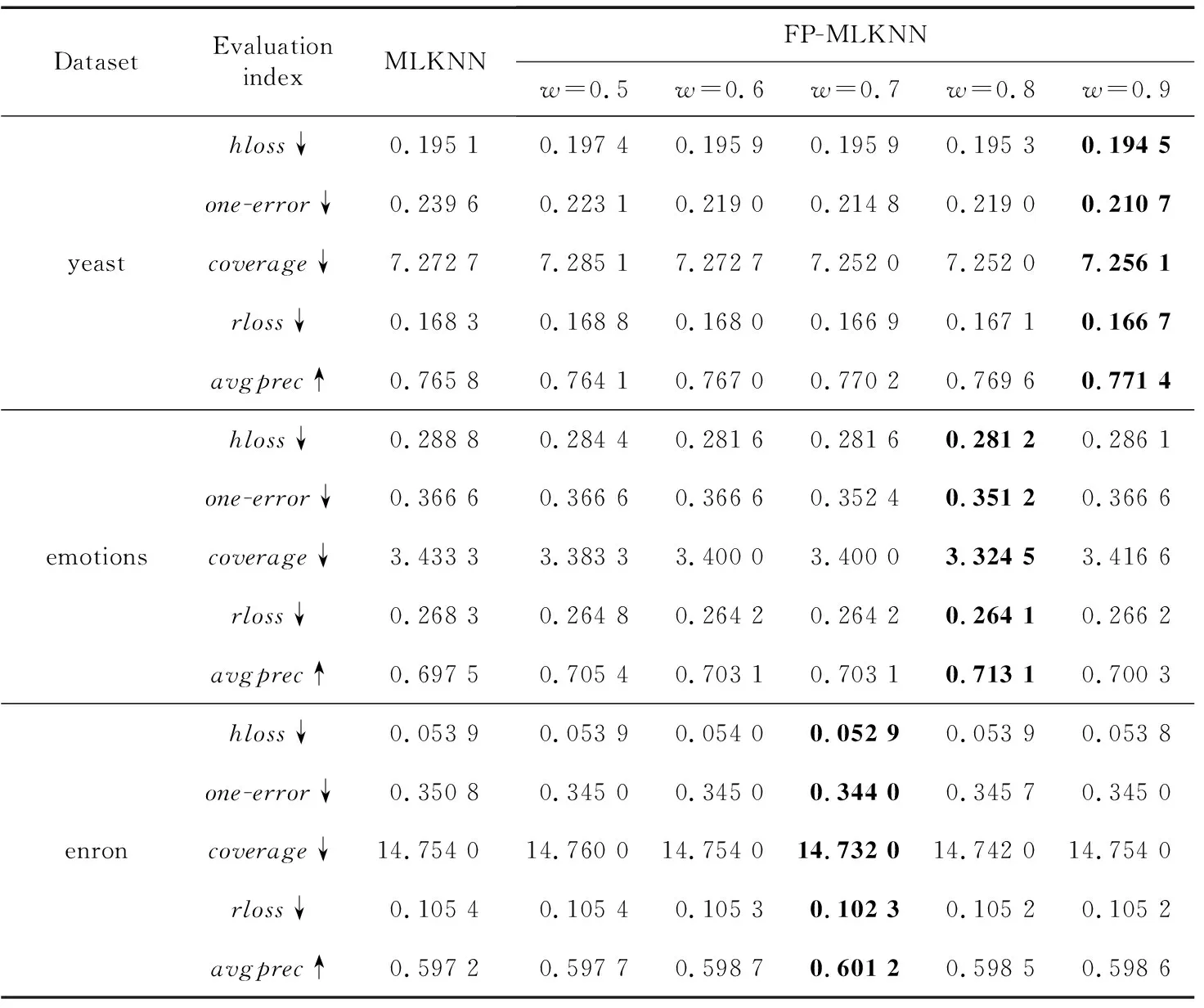
Table 4 Comparison of experimental results between the original algorithmand the improved algorithm with differentwvalues whenk=10

如表5所示，将改进后的算法FP-MLKNN与其他多标签分类算法MLKNN、BPMLL和AdaBoostMH进行实验对比，其中 MLKNN 和 AdaBoostMH 算法属于一阶处理方法，BPMLL是二阶处理方法。实验中FP-MLKNN和MLKNN的k取值都为10，FP-MLKNN算法在yeast、emotions、enron数据集上w的取值分别为0.9,0.8,0.7。从实验对比可知，本文提出的基于关联规则的MLKNN多标签分类算法FP-MLKNN在3个数据集上的性能均优于其他多标签分类算法的，这说明了本文所提出的基于关联规则的MLKNN多标签分类算法的科学性和准确性。

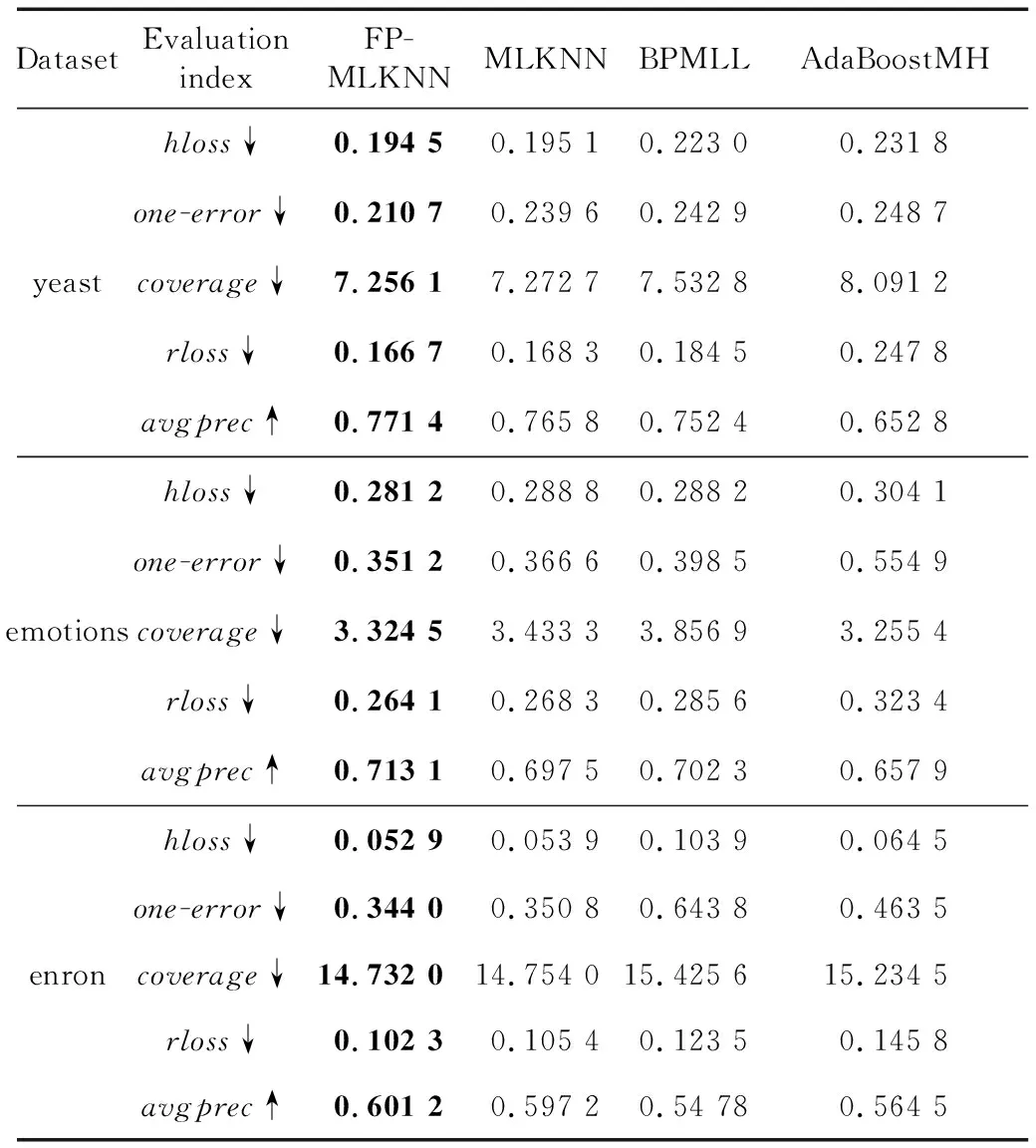
Table 5 Experimental comparison ofmulti-label classification algorithms

5 结束语

在多标签学习中，标签之间的相关性是一个不可忽略的因素，已有的MLKNN算法并没有考虑标签之间的相关性。为了充分利用标签之间的相关性来优化多标签分类算法的性能，本文提出了一种基于关联规则的MLKNN多标签分类算法FP-MLKNN。针对多标签数据考虑标签与标签之间的相关性，采用关联规则算法挖掘标签之间的高阶相关性，将标签之间的关联规则应用到MLKNN算法改进中。在具体实施中，采用改进后的算法对yeast、emotions和enron 3个数据集进行实验，并将改进后的算法FP-MLKNN与其他多标签分类算法MLKNN、BPMLL和AdaBoostMH进行实验对比，实验结果表明，本文所提出的基于关联规则的MLKNN多标签分类算法极大地提高了多标签数据分类的准确性。