伽罗瓦连接在构造拟阵中的应用*

王 刚,毛 华,武振宇

(1.河北大学生命科学学院,河北 保定 071002;2.河北大学数学与信息科学学院,河北 保定 071002)

1 引言

拟阵是由Whitney[1]于1935年提出的，构造拟阵是其研究内容之一。伴随着拟阵在许多领域的应用[2 - 20]，原始的拟阵结构[1]在不断地扩展[14 - 18]。从这些拟阵的扩展过程推测，将处理数据的理念用到拟阵论研究中是可行的。事实上，如何将处理数据的有效方法应用到构建拟阵结构，促使拟阵论以更多方式应用到数据处理中，是目前拟阵论研究中需解决的问题之一。

伽罗瓦连接(Galois Connection)根植于伽罗瓦理论，由背景(Context)产生。该定义不仅在形式概念分析(或称概念格FCA(Formal Concept Analysis))中得以应用[12,13,21 - 24]，而且还在数据挖掘等领域也有运用[25 - 29]。概念格理论是由Wille[30]始创的，是支持数据分析的一种有效工具。构建概念格是其研究内容之一，现已有不少有关的算法[21,22,31 - 33]。近来，人们关注背景与映射之间的关系问题，以及背景与完备格、闭包算子和拟阵之间的关系等问题，取得了不少成果[9 - 12,21,22,34 - 43]。

为探讨拟阵、伽罗瓦连接、概念格和背景之间内在作用，已有学者研究在一些拟阵和一些概念格之间的关系[9 - 11,43]，以及利用与贪心算法有关的方法[2,3,15 - 18,44]找到一些特殊背景下的概念格[45,46]，还有用粗糙集理论等构建拟阵结构[8,36]。

综上可知，需要有更新的方法融入到构造拟阵的研究中。虽然构造概念格的方法很多，但是构造拟阵的方法相对较少。如果改变这个现状，那么对拟阵的发展和应用必会起到推动作用，对FCA理论应用领域的扩大也会有效。为此，分析已有的一些相关性质是必要的，现总结如下：(1) 由拟阵闭包公理可知，1个拟阵可由1种特殊的闭包算子唯一确定[2,3]。(2) 结合已有结果[7,9 - 13,20 - 22]确信，拟阵有能力成为研究FCA的一个工具，而FCA中的一些结果也能应用到拟阵研究中。(3) 从概念格定义可知[21,22]，对1个背景(O,P,R)，存在2个映射′和′：一个是定义在P(O)上的′，另一个是定义在P(P)上的′。(O,P,R)的概念格就是由构成1对伽罗瓦连接[21,22]的映射(′,′)所决定的。

由(1)～(3)可知：深入的研究需找到拟阵与背景之间的深层关系，而关键问题是：对于以σ为闭包算子的集合O上的拟阵，以及1个背景(O,P,R)上所产生的1对映射(′,′)，在何种条件下有σ=′′成立？为寻找到此问题的答案，首先分析已有的一些相关结果：(1)文献[2,3]给出了拟阵与几何格之间的关系;(2)文献[3,47]给出了有向拟阵的格理论特征;(3)文献[4,48]分别给出了格论与Coxeter拟阵之间的一些关系线索；(4)文献[21,22]得到了背景与格论之间的关系，还得到完备格与概念格之间有相互对应的关系；(5)文献[10]利用简单拟阵的闭集族的格论性质，给出简单拟阵与某些背景之间的关系。

综合这些结果可推断：伽罗瓦连接和格论在探讨拟阵的构建中会起到重要作用，或许通过这种作用可找到上述关键问题的答案。本文研究将沿此思路进行。具体工作如下所示：(1) 借助伽罗瓦连接揭示背景与拟阵之间的关系；(2) 找到由1个拟阵构造伽罗瓦背景的方法；(3) 找到由1个伽罗瓦背景建立拟阵的一些方法；(4) 用实例说明所得方法的有效性。

本文其余安排如下：第2节说明后续工作所需定义和术语；第3节挖掘伽罗瓦背景与拟阵之间的关系，给出所求关键问题的答案；借用构造概念格的一些已有方法，在第4节将得到建立拟阵的一些方法；第5节为实例；第6节为结束语。规定本文所讨论的内容均为有限。

2 预备知识

设S为1个集合，用P(S)代表S的所有子集构成的集合。

定义1(1)令O和P为2个集合，R⊆O×P。若X⊆O，Y⊆P，则令K(X)={y∈P|∀x∈X，(x,y)∈R}；L(Y)={x∈O|∀y∈Y，(x,y)∈R}。称这对映射(K,L)是O和P之间的1个伽罗瓦连接[49]。若J:P(O)→P(O)满足条件①～③，则称J为O上的1个闭包算子。令X,Y⊆O，有：①X⊆J(X)；②X⊆Y⟹J(X)⊆J(Y)；③J(J(X))=J(X)。

对于X∈P(O)，若J(X)=X，则称X为闭的。闭包算子J的所有闭集构成的集合记为B(J)。

(2)设M1=(E1,I1)和M2=(E2,I2)是2个拟阵，其中Ij为Mj的独立集族。若存在双射f:E1→E2满足：X∈I1⟺f(X)∈I2，则称M1和M2是同构的，记为M1≌M2[2,3,50]。

说明1(1) 定义1中的伽罗瓦连接和闭包算子，均与文献[21,22]中相关内容一致。

(2)定义1(1)中称(K,L)为1个伽罗瓦连接是对的，因其与伽罗瓦理论中相关内容[51]一致。

有关格论的内容参见文献[21,22,52]。下面给出FCA的内容，未尽事宜参见文献[21,22]。

定义2(1)一个背景是指1个3元组(O,P,R)，其中的O和P是集合，R⊆O×P。对于A⊆O和B⊆P，定义A′={m∈P|∀g∈A，(g,m)∈R}，B′={g∈O|∀m∈B，(g,m)∈R}。称(′,′)为(O,P,R)衍生的1对算子。若A′=B且B′=A，则称(A,B)为(O,P,R)的一个概念(Concept)。(A,B)的外延是A，内涵是B。(O,P,R)的所有概念集合记为Gal(O,P,R)[21,22]。

(2)设(Oj,Pj,Rj)为1个背景(j=1,2),f:O1→O2和g:P1→P2为1对双射。若(f,g)满足：(n,m)∈R1⟺(f(n),g(m))∈R2,则称(O1,P1,R1)同构于(O2,P2,R2)，记为(O1,P1,R1)≌(O2,P2,R2)[21]。

引理1设O和P为2个集合，R⊆O×P。

(1)令K:P(O)→P(P),L:P(P)→P(O)为1个伽罗瓦连接，则LK为O上的闭包算子[49]。

(2)设(′,′)为定义2中给出的(O,P,R)衍生的1对算子，则(′,′)形成1个伽罗瓦连接[21]。

说明2从定义1、定义2和引理1(2)可得，对一背景(O,P,R)，必存在O和P之间的1个伽罗瓦连接(K,L)。有时也称(K,L)是从(O,P,R)产生的，或说(K,L)是对应于(O,P,R)的。

引理2(1)由Gal(O,P,R)产生1个格结构，将此格称为概念格(Concept Lattice)，或称伽罗瓦格，仍记为Gal(O,P,R)[21,22]。

(2)令BO:={A⊆O|A″=A}，则BO是(O,P,R)外延的全体，并且(BO,⊆)是1个同构于Gal(O,P,R)的格，称(BO,⊆)为外延格，简记为BO[22]。

引理3设(O,P,R)为1个背景。若(K,L)为对应于(O,P,R)的1个伽罗瓦连接。(′,′)为定义2中给出的，由(O,P,R)衍生的算子，则LK=″。

证明由引理1(2)知，(′,′)形成1个伽罗瓦连接。再考虑定义2得：对于X⊆O有X′={y∈P|对于任何x∈X都有(x,y)∈R},进一步地有(X′)′={a∈O|对于任何b∈X′都有(a,b)∈R}。根据已知条件，(K,L)为对应于(O,P,R)的1个伽罗瓦连接。再考虑定义1得：对于X⊆O有K(X)={y∈P|∀x∈X，(x,y)∈R}。进一步地有，L(K(X))={c∈K(X)|∀d∈K(X)，(c,d)∈R}。对比(X′)′和L(K(X))得(X′)′=L(K(X))。若简记(X′)′为(X)″，L(K(X))为LK(X)，则有(X)″=LK(X)。又据X的任意性，必有LK=″。

□

说明3设(O,P,R)为1个背景，(K,L)为对应于(O,P,R)的伽罗瓦连接。

(1) 由定义1和定义2确信：对∀X⊆O和∀Y⊆P有K(X)=X′和L(Y)=Y′。再由引理3得BO=B(LK)。

(2) 引理3说明，上面(1)蕴含着：对应(O,P,R)的伽罗瓦连接是唯一的。

此处利用文献[2,3]给出拟阵的一些性质。有关拟阵的其它内容参见文献[2,3]。

引理4令M为集合E上的1个拟阵，且F为其闭集族。

(1)P(E)上的1个函数σ是M的闭包算子，当且仅当σ为E上的1个闭包算子，并且满足条件(s4)：对于任何的Y∈E以及y,z∈E，若y∉σ(Y)但是y∈σ(Y∪z)，则z∈σ(Y∪y)[2,3]。

(2)(F,⊆)是1个几何格[2,3]。

(3)由几何格L产生的定义在L的原子集合上的拟阵M(L)，这一对应是有限几何格族与简单拟阵族之间的1个双射[2]。

说明4根据引理4(1)，本文用(E,σ)表示集合E上的1个拟阵M，其中σ为M的闭包算子。虽然由定义1和引理4(1)知，σ是P(E)上的1个闭包算子，但是E上任一个闭包算子J不一定是E上的某拟阵的闭包算子。由定义1(2)以及引理4(1)可知，对于2个拟阵M1=(E1,σ1)和M2=(E2,σ2)，若M1≌M2，即存在M1到M2的同构映射f，则对∀X⊆E1有：X=σ1(X)⟺f(X)=σ2(f(X))。

3 伽罗瓦连接与拟阵的关系

本节要找到伽罗瓦连接与拟阵之间的关系。挖掘用拟阵的闭包算子建立拟阵的方法，它们不同于以往的方法[2-4,8,10,12,13,36,53,54]。本节结果将会回答第1节提出的关键问题。

首先给出1个定义。

定义3设(O,P,R)为1个背景，(K,L)为由(O,P,R)产生的伽罗瓦连接。若(O,LK)是1个拟阵，则称(O,P,R)为1个伽罗瓦背景。

注1(1) 根据引理2(1)和文献[21,22]可知：为了获得关键问题的答案，需要关注伽罗瓦背景。

(2) 由引理3、定义1和定义3，下文视情况讨论伽罗瓦连接与拟阵的关系和背景的伽罗瓦性质。

下面的引理将保证：对于1个给定的拟阵一定存在1个与其相关的伽罗瓦背景。

引理5设M=(O,σ)为1个拟阵，定义R⊆O×P(O)为：对于x∈O和Y⊆O，有(x,Y)∈R⟺x∈σ(Y)。若(K,L)为由背景(O,P(O),R)产生的伽罗瓦连接，则σ=LK。

证明分2步完成证明。

步骤1 证明(O,P(O),R)是1个背景。

由定义2(1)以及R的定义可得所需。

步骤2 证明σ=LK。分2方面进行。

一方面证：LK⊆σ。令X⊆O且x∈X。则由定义1知：K(X)={Z⊆O|∀x∈X,(x,Z)∈R}且L(K(X))= {a∈O|∀Z∈K(X),(a,Z)∈R}。又由引理4和定义1得x∈σ(X)。因此，σ(X)∈K(X)。令a∈L(K(X))且U∈K(X)。依据LK和R的定义有a∈σ(U)成立。再由σ(X)∈K(X)，可得a∈σ(X)。故L(K(X))⊆σ(X)。

另一方面证明：σ⊆LK。令X,Z⊆O，对于任意的x∈X，若x∈σ(Z)，则X⊆σ(Z)。进而根据定义1(1)和引理4(1)必有σ(X)⊆σ(σ(Z))=σ(Z)。因此，若b∈σ(X)，则有：对于任意Z∈K(X)有b∈σ(Z)。所以有(b,Z)∈R。故而，b∈L(K(X))成立。即有σ(X)⊆L(K(X))。

□

注2运用构造性的方法，引理5给出从1个拟阵产生一个伽罗瓦背景的方法。该引理也说明定义3是有意义的。

考虑引理5的逆命题是否成立?答案是不一定。原因如下：

(1)例1表明对某些伽罗瓦连接(K,L)，必有1个以LK为其闭包算子的拟阵。

例1令(O,P,R)为1个背景，满足R=O×T，此处T⊆P。令(K,L)是由(O,P,R)产生的伽罗瓦连接。由定义1，对于任意的X⊆O，必有K(X)={y∈P|∀x∈X,(x,y)∈R}=T且L(K(X))=O。因此，易得LK满足引理4(1)中的条件(s4)。从而由引理4(1)知：M=(O,LK)是1个拟阵，并且B(LK)= {O}。

(2)如果假设引理5的逆命题总是成立，那么讨论如下：令(O,P,R)为1个背景。由于定义1和说明3(2)，存在且仅存在1个从(O,P,R)产生的伽罗瓦连接(K,L)。根据引理1，LK是O上的1个闭包算子。假设M=(O,σ)是1个拟阵且σ=LK。由定义1和引理4(1)知M的所有闭集集合F为{X⊆O|σ(X)=X}。又由定义1知：LK的所有闭集的集合B(LK)={X⊆O|LK(X)=X}。故由σ=LK有F=B(LK)。依据引理4(2)，(F,⊆)是1个几何格。这导致(B(LK),⊆)是几何的。结合说明3(1)得BO=B(LK)，有(BO,⊆)是几何格。再用引理2知格Gal(O,P,R)是几何的。然而对任一背景(O1,P1,R1)，格Gal(O1,P1,R1)不一定是几何的[10]。这就导致矛盾。该矛盾说明引理5的逆命题不成立。

基于此，下方引理将会发现，何种条件下1个伽罗瓦连接(或说1个背景)可创建1个拟阵。

引理6设(O,P,R)为1个背景，(K,L)为由(O,P,R)产生的伽罗瓦连接。如果LK满足条件(s4)，那么(O,LK)是1个拟阵。

证明根据说明3(2)知，(K,L)=(′,′),再由引理3有LK=″。从引理1得知：LK为集合O上的1个闭包算子，进一步地，据引理4(1)，以及LK满足条件(s4)，可确信(O,LK)为1个拟阵。

□

引理6看上去简单，但却是判定(O,LK)为拟阵的基础。

接下来，将继续讨论拟阵与伽罗瓦连接之间的关系问题。

例2设(O,P,R1)和(O,P,R2)为2个背景，此处，对于某个t∈P和T2⊆P满足T2 ≠∅有R1=O×{t}且R2=O×T2。设(Kj,Lj)(j=1,2)为对应于(O,P,Rj)的伽罗瓦连接。显然，R1≠R2使得(K1,L1)和(K2,L2)之间存在差异。然而，例1的结果保证：LjKj是拟阵Mj=(O,LjKj)的闭包算子(j=1,2)。类似地，对于任意的X⊆O必有L1K1(X)=O=L2K2(X)。因此，由引理4(1)和L1K1=L2K2得到：M1=M2成立。

例2表明，不同的伽罗瓦背景可能产生相同的拟阵。下面将讨论在何种条件下，可以克服这个非唯一性。先引入如下的定义。

定义4[12]设(Oj,Pj,Rj)为1个背景，其相应的伽罗瓦连接为(Kj,Lj)，j=1,2。若存在1个双射π：O1→O2满足：对于任意的X⊆O1有：X=L1K1(X) ⟺πX=L2K2(πX)。则：(1) 称(K1,L1)是伽罗瓦同构(Galois Isomorphic)于(K2,L2)，记为(K1,L1)≌G(K2,L2)；(2) 称π为(K1,L1)和(K2,L2)之间的1个伽罗瓦同构映射；(3) 称π为(O1,P1,R1)与(O2,P2,R2)之间的1个伽罗瓦同构映射；(4) 称(O1,P1,R1) 是伽罗瓦同构于(O2,P2,R2)，记为(O1,P1,R1)≌G(O2,P2,R2)。

说明5(1)文献[2]指出，对于2个拟阵M1=(O1,σ1)和M2=(O2,σ2)，即使(F1,⊆)≌(F2,⊆)，仍不能够保证存在1个双射π0：O1→O2满足：X∈F1⟺π0(X)∈F2。即此时不能够保证有M1≌M2。

(2) 对于背景(O,P,R)，最实质的研究是：构造格Gal(O,P,R)(或者在格同构意义下构造(BO,⊆))。从说明2和引理3可以发现，若(K,L)是从(O,P,R)产生的伽罗瓦连接，则有BO=B(LK)。

(3)文献[12]指出：(O1,P1,R1)≌(O2,P2,R2)⟹(O1,P1,R1)≌G(O2,P2,R2)，但反之不然。这表明，伽罗瓦同构是比同构要求条件弱的一种形式。

为了处理背景与拟阵之间的关系，需要下面的拟阵和伽罗瓦背景的性质：

引理7[12](1) 设(Oj,Pj,Rj)为对应于1个拟阵Mj=(Oj,σj)的伽罗瓦背景，并且(Kj,Lj)为从(Oj,Pj,Rj)产生的伽罗瓦连接，j=1,2。那么M1≌M2⟺(O1,P1,R1)≌G(O2,P2,R2)。

(2) 设(Oj,Pj,Rj)为一个背景且(Kj,Lj)为与其对应的伽罗瓦连接，j=1,2。那么(K1,L1)≌G(K2,L2)⟺(O1,P1,R1)≌G(O2,P2,R2)。

定义3、定义4和引理7结合可得到下面的结果：

定理1在伽罗瓦同构和拟阵同构意义下，伽罗瓦背景族与拟阵族之间存在1个双射。

证明令Mj为集合Oj上的拟阵，且σj为其闭包算子，j=1,2。由引理5可发现1个由Mj产生的伽罗瓦背景(Oj,P(Oj),Rj)，j=1,2。若M1≌M2，则据引理7(1)有(O1,P(O1),R1)≌G(O2,P(O2),R2)。

反之，令(Oj,Pj,Rj)为1个伽罗瓦背景，(Kj,Lj)为由(Oj,Pj,Rj)产生的伽罗瓦连接，j=1,2。那么由定义4知：存在1个定义在Oj上的拟阵Mj，满足LjKj为其闭包算子，j=1,2。若(O1,P1,R1)≌G(O2,P2,R2)成立，则由引理7(1)有M1≌M2成立。

□

推论1在伽罗瓦同构与拟阵同构意义下，由伽罗瓦背景产生的伽罗瓦连接族与拟阵族之间，存在1个双射。

证明考虑定理1、定义3、定义4和引理7(2)，很容易得到所需结论。

□

注3(1) 结合说明3(2)可以断言：定理1和推论1回答了第1节提出的关键问题。

(2) 定理1和推论1提供了将拟阵理论应用到伽罗瓦连接研究中的坚实基础。

说明6(1) 对背景(O,P,R)，引理5的逆命题不成立，故或许无拟阵M=(O,σ)满足σ=LK，其中(K,L)为(O,P,R)产生的伽罗瓦连接。这与例1之后的(2)结果一致。这也说明了定理1的正确性。

(2) 在伽罗瓦同构与拟阵同构意义下，存在唯一1个拟阵对应于伽罗瓦背景(O,P,R)。

4 伽罗瓦连接构造拟阵的方法

现已知的一些构造拟阵算法分别依据拟阵的独立集公理[2,3,50,53]、覆盖图[10]、格结构[6,12]等[8,36]原理完成算法过程。据拟阵的定义[2,3,50]，对1个分别以I，F为其独立集族和闭包集族的拟阵，必有|F|≤|I|。所以第3节是有意义的。本节将提供2种利用伽罗瓦连接建造拟阵的方法。

算法1构造M的算法

输入：(O,P,R)为1个背景。

输出：是否有1个拟阵M，且LK为M的闭包算子。

步骤1找到BO(也就是B(LK))，即{X⊆O|X=LK(X)}。

步骤2对于任意的X∈B(LK)和a,b∈O，若a∈LK(X∪b)LK(X)成立，则检查是否有b∈LK(X∪a)。若为是，则转步骤3,否则转步骤4。

步骤3由引理4(1)知B(LK)为O上拟阵M=(O,LK)的闭集族。

步骤4由定理1知LK不为O上任何拟阵的闭包算子。

说明7(1) 已有的得到BO的算法(或者由说明3(1)等价地说，得到B(LK)的算法，或者由引理2(2)等价地说，得到Gal(O,P,R)的方法)[21,22,32,33]，其中任一个都可完成步骤1中的任务。

(2) 由引理 6，若要构造1个拟阵(O,σ)满足σ=LK，则需执行步骤2。

(3) 事实上，到现在为止，用拟阵的闭集族的性质构建1个拟阵的方法不多[10,12,13]。虽然已有在同构意义下，找到1个闭包算子的所有闭集的方法[55]，但是对于1个具体的问题，文献[55]给出的算法，对于有附加要求的结构性质来说通常不作考虑。因此可以断定：算法1可成功地利用伽罗瓦连接的闭集族完成拟阵构建。

(4)在已有的方法中[21,22,32,33]，NextClosure算法[21]是得到BO的最著名算法。对于任何A⊆O,得到A+∈BO的算法时间复杂度是O(|O||P|2)，这是线性时间，从而也是一个多项式时间。得到BO的全体，即{A+|A⊆O}的时间复杂度为O(|O||P|2|BO|)。对于X∈BO，步骤2的时间复杂度为O(|O|2)，因此步骤2的时间复杂度为O(|O|2|BO|)。由于|BO|≤2|O|，所以算法1的时间复杂度为O(|O|(|O|+|P|2)2|O|)。再因为已知常用的求BO的算法中，在时间复杂度方面，NextClosure算法是较低的。即便如此，读者可根据问题的实际情况和喜好方便程度，决定采用哪一种方法完成步骤1。若设步骤1的时间复杂度为C，则算法1的复杂度为O(|O|22|O|+C)。

算法2构造O上1个拟阵

输入：(O,P,R)为1个背景。

输出：是否有1个以LK为闭包算子O上的1个拟阵M。

步骤1用已有的方法，或者如文献[56]中的软件,得到格Gal(O,P,R)，再可得到(BO,⊆)，即(B(LK),⊆)；或者采用1个已有的直接得到(BO,⊆)的方法，即得到(B(LK),⊆)。

步骤2判断(B(LK),⊆)是否为几何的。若是，则转步骤3；若否，则转步骤4。

步骤3在同构意义下，B(LK)是O上的1个拟阵M的闭集族并且LK为其闭包算子。

步骤4由引理4(3)，得出在O上不存在1个拟阵M以LK为其闭包算子。

说明8(1) 根据已有的讨论[2,3,52]，要完成步骤2，需要完成下面2项判定工作。第1项：(B(LK),⊆)中的每1个元都是原子(即在(B(LK),⊆)中覆盖最小元的元)的并。第2项：在(B(LK),⊆)中，对任何x,y∈B(LK)都有：x和y覆盖x∧y⟹x∨y覆盖x和y。

(2) 当得(B(LK),⊆)时，第1项完成。故可在进行第1项工作时，直接选择能够生成(B(LK),⊆)的格图(即Hasse示图)的方法，例如文献[56]中给出的方法,可以很快得到(B(LK),⊆)的原子集。

(3) 由文献[2,3,52]，第2项工作可等价地陈述为：在(B(LK),⊆)中，任何2个元x,y之间的极大链有相同的长度且h(x)+h(y)≥h(x∧y)+h(x∨y)，此处h为高函数。从定义发现，在时间复杂度方面，判断极大链的长度和得到h与第2项工作一致，故可根据实际问题选择第2项的具体方法。

(4) 虽然文献[56]是公开的，但在时间复杂度方面并无公开信息。步骤2的时间复杂度为O(2|B(LK)|)。文献[22]中BO和(BO,⊆)同时产生的算法时间复杂度为O(2|O||P|)。但是，该方法尚未找到对应的软件。

算法1和算法2比较如下：

(1) 2个算法的步骤2在时间复杂度上都是O(2|B(LK)|)，故无太大区别，只是方法上有所不同。

(2) 2个算法的步骤1均需找B(LK)。算法1无需从(B(LK),⊆)上寻找某种性质，故对任何生成B(LK)或Gal(O,P,R)的方法，都可使用。算法2需考虑(B(LK),⊆)的原子全体，故为了使所得(B(LK),⊆)的结果中，其原子全体可以直观地显示出来，建议在选择算法或软件时，采用可以直接生成(B(LK),⊆)的全体，又可同时得到(B(LK),⊆)的Hasse示图的算法或软件。

(3) 算法1产生的拟阵是唯一的，但不一定是简单的。算法2得到的拟阵一定是简单的，且在拟阵的同构意义下和格的同构意义下，得到的拟阵是唯一的。

说明9由于本文中给出的2种构造拟阵的算法，利用了处理数据的有效工具FCA中一些理念和思想，所以当将算法1和算法2与已知的方法比较时，选取的对比方法也须是与处理数据有关的方法，这样才会更有说服力。在已有的研究成果中，文献[10，12]的方法相对更好一些。

算法1和算法2与一些已知方法的比较结果如表1和表2所示。

Table 1 Comparison between algorithm 1and method in reference [12]

Table 2 Comparison between algorithm 2and method in reference [10]

从表1和表2可以总结如下：

(1) 从计算机的辅助工作方面：算法1和算法2优于文献[10]和文献[12]的。

(2) 可以推测：算法1和算法2在未来的工作中，必会结合其它理论和想法，应用到FCA的探索中，而文献[10]和文献[12]的方法则不一定。

(3) 算法1构造的拟阵不一定是简单的，文献[10]的方法得的拟阵一定是简单的，所以算法1比文献[10]中的方法适用范围更广。在实现过程中，算法2的工作量小于文献[10]的方法的工作量。

(4) 算法1和算法2是直接产生拟阵，而文献[12]的方法在数据的存储空间上比算法1和算法2的都大。

5 应用举例

本节通过实际例子说明第4节给出的算法的应用与实现。

例3采用文献[10]中表2的数据,其对应的数学表示如表3所示。

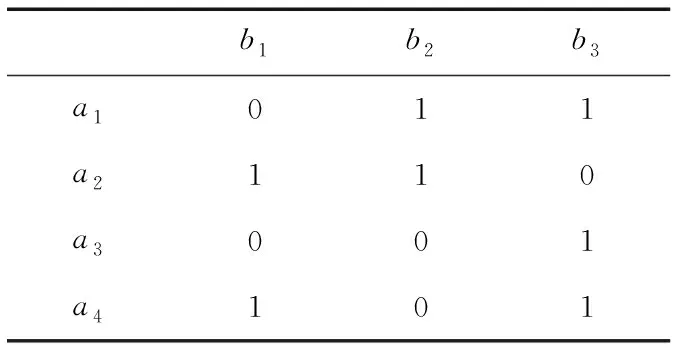
Table 3 Mathematical representation oftable 2 in reference [10]

下面将用算法2构造该背景的拟阵。利用文献[56]的软件得到表3对应的形式背景(O,P,R)的伽罗瓦格，如图1所示，其中O={aj:j=1,2,3,4}，P={bj:j=1,2,3},R如表3所示。其中，R⊆O×P,aiRbj在表3中对应的值为1，否则为0(i=1,…,4,j=1,2,3),在表3中，a1=钩刺豆芫菁，a2=墨江豆芫菁，a3=扁角豆芫菁，a4=戈勒姆豆芫菁，b1=体腹侧并不全都散布黑毛，b2=体背侧主要散布棕毛，b3=体腹侧散布有黑色长毛，0为“是”，1为“否”。

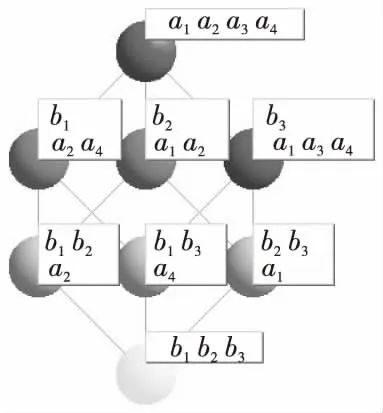
Figure 1 Galois lattice of (O,P,R)图1 (O,P,R)的伽罗瓦格

由BO和Gal(O,P,R)的关系，立刻得到：BO={{∅},{a1},{a2},{a4},{a1,a2},{a2,a4},{a1,a3,a4},{a1,a2,a3,a4}}。利用Gal(O,P,R)≌(BO,⊆)，以及BO=B(LK)可得(B(LK),⊆)的原子集是{{a1},{a2},{a4}}。还可以直接获得(B(LK),⊆)中其他非最小元的元与原子的关系，进而可知(B(LK),⊆)是一个几何格。由算法2中的步骤3可知，(O,LK)为1个拟阵，并且B(LK)是该拟阵的闭集族，LK是该拟阵的闭包算子。

说明10将例3与文献[10]中的例2相比较可知，对于同一个背景，由于算法2与文献[10]构造拟阵的方法不同，得到的拟阵不一样，也说明算法2是一个创新的方法。

例4用文献[57]中表3给出的数据，其对应的数学表示如表4所示。易知(O={aj:j=1,…,16},P={bj:j=1,…,9},R1)为1个背景，R1如表4所示。R1⊆O×P,aiR1bj在表4中对应的值为1，否则为0(i=1,…,16;j=1,…,9)。

Table 4 Mathematical representation oftable 3 in reference [57]

令S⊆{aj:j=1,…,16}×{bj:j=1,…,9}定义为：xSy⟺{x}′={y}′。易证S为等价关系，且由定义2(1)得：[a1]S={a1},[a2]S={a2,a15},[a3]S={a3},[a4]S={a4,a5,a6,a8,a13},[a7]S={a7},[a9]S={a9,a10},[a11]S={a11,a12},[a14]S= {a14},[a16]S={a16},其中[x]S为关于S的x所在的等价类。令[a1]S=o1,[a2]S=o2,[a3]S=o3,[a4]S=o4,[a7]S=o5,[a9]S=o6,[a11]S=o7,[a14]S=o8,[a16]S=o9。由表4得到依S产生的聚类背景表，如表5所示。 则得背景(O1={oj:j=1,…,9},P={bj:j=1,…,9},R2)，R2如表5所示。R2⊆O1×P,oiR2bj在表5中对应的值为1，否则为0(i=1,…,9;j=1,…,9)。

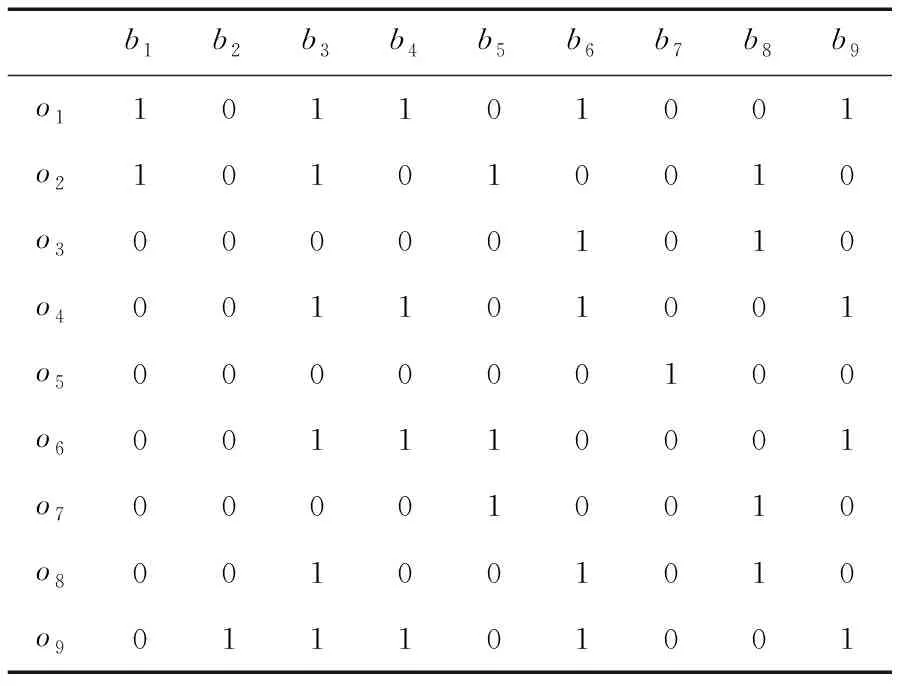
Table 5 Clustering context produced from table 4 based onS

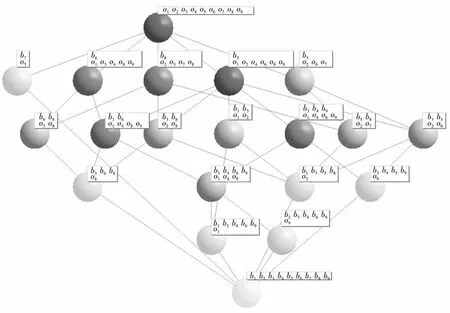
Figure 2 Galois latticeGal(O1,P,R2) corresponding to table 5图2 表5的伽罗瓦格Gal(O1,P,R2)

根据文献[56]可以得到表5的伽罗瓦格Gal(O1,P,R2)如图2所示。由B(LK)与Gal(O1,P,R2)的关系可得B(LK)={{∅},{o1},{o2},{o5},{o6},{o8},{o9},{o3,o8},{o2,o6},{o2,o7},{o1,o2},{o2,o8},{o1,o4,o9},{o2,o6,o7},{o1,o4,o8,o9},{o1,o4,o6,o9},{o2,o3,o7,o8},{o1,o3,o4,o8,o9},{o1,o2,o4,o6,o8},{o1,o2,o3,o4,o5,o6,o7,o8,o9}}。取X={o1}，则X∈B(LK)且LK(X)=X。取o8,o9∈O1，则o8,o9∉LK(X)。因LK(X∪o9)=LK({o1,o9})={o1,o4,o9}，LK(X∪o8)=LK({o1,o8})={o1,o4,o8,o9}，故o9∉LK(X∪o8)，而o8∉LK(X∪o9)。由算法1知：LK不为O1上任何拟阵的闭包算子。

说明11(1) 在生物聚类分析中，若2个样本具有完全相同的生物特征，则认为两者为一类。例4中的二元关系S在生物上是有意义的。

(2) 虽然例4中LK不为O1上任何拟阵的闭包算子，进一步地，伽罗瓦格Gal(O,P,R1)与Gal(O1,P,R2)是同构的[21,22]。故在昆虫聚类分析中，对表4的分析也可说是对表5的聚类分析。对表4的聚类分析中，目前生物学家们常用聚类图一种树状结构图，表示分析的结果。又由树为一个无圈简单图，由此可以得该树的圈拟阵[2,3,50]，该拟阵的独立集族与闭集族完全一致。

(3) 从文献[57]中对于表4的聚类结果，即文献[57]中的图1可知，将该图从左向右看，图中最上的坐标标尺为l,则可以得到以下结论：第0层(l=0)组成元有：{aj},j=1,…,16；第1层(l=1)组成元有：{[aj]S},j=1,…,16；第2层(0

从组成元与图2对比可知：第0层为表4的对象集；第1层为表5的对象集；第2层中{[a3]S,[a14]S}为{o3,o8}在图2的对应节点，文献[57]中图1得到此点是根据[a3]S和[a14]S有共同的生物特征b6和b8，而在图2中此节点为(o3o8,b6b8)。

事实上，拥有b3和b6昆虫的是为{o1,o4,o8,o9}={[a1]S,[a4]S,[a14]S,[a16]S}={a1,a4,a5,a6,a8,a13,a14,a16}。即文献[57]中的图1没能将拥有生物特征b3和b6的所有昆虫全部找出来。图2中{o1o4o8o9,b3b6}恰好将所有拥有生物特征b3和b6的昆虫全部显示的1个节点。继续分析文献[57]的图1中第k层组成元(k=3,…,8)也会出现类似于上述关于第2层分析的情况。另外，图2还给出了文献[57]图1中没有出现的其它一些节点，如(o1o3o4o8o9,b6)，它们在生物上也是有意义的，这里不再展开。分析发现图2在生物上是有意义的。图2也是一个图，一定存在多个生成树，哪一个生成树更能体现所研究的生物背景的聚类结构，将是今后数学和生物学者们共同考虑研究的问题。

6 结束语

通过分析拟阵、背景、伽罗瓦连接、闭包算子之间的关系，得到背景之间同构定义的一种拓广形式，即伽罗瓦同构。进一步地，得到在何种条件下，一个拟阵的闭包算子为一个背景产生的伽罗瓦连接。再者，用这种关系，得到由伽罗瓦连接构建拟阵的2种方法。

在未来：(1) 对背景(O,P,R)，将会研究如何选取已有构造概念格的算法，找到检查(O,P,R)是否为一个伽罗瓦背景的新算法。(2)在伽罗瓦背景或说在伽罗瓦连接帮助下，得到新的拟阵闭包公理，搜寻到更多拟阵族的格结构。(3)考虑将拟阵应用到生物聚类分析的研究中。