自适应远光照明均匀性的解决方案

郭壮柱，杨志，庞宏力，郭青杰

(曼德电子电器有限公司保定光电分公司，河北 保定 071000)

引言

随着照明技术的发展[1]，汽车灯具变得越来越智能[2]，逐渐从最初的被动式照明向主动安全式照明方向发展[3]，并且随着整车网联智能化的发展，汽车灯具的安全照明在自动驾驶的发展过程中显得尤其重要，例如车灯的自适应远光(adaptive driving beam，ADB)功能[4-6]，使驾驶者便于看清前方路况的同时也避免了前方车辆内驾驶者的眩目[7]。对于智能防眩目远光的设计，存在一个矛盾点——防眩目远光整体光型的均匀性与单个分区防眩目角度的矛盾，此矛盾点在低分区数量的光型中表现得尤其明显。当要保证分区精度的前提时，相邻两个分区则需叠加角度较小，从而极易产生明暗相间的条纹；当要保证远光整体光型均匀时，相邻两个分区则需叠加角度较大，但分区间的相互影响变大，导致防眩目角度成倍的增加[8]。

针对此矛盾点，可通过提高分区的精细度来降低矛盾程度，遮蔽眩目区域的角度占整体光型的百分比较小，可实现效果较佳的防眩目效果，但此种方案需要分区数量至少为20个，价格相对较高，针对普通车型应用较为困难。对此，本文通过对矛盾点的介绍，提出一种新的ADB设计思路——逆向设计思维，从整体光型着手进行设计，针对此矛盾点对每个分区的光强进行推导计算，使得分区数量较少的情况下中和此矛盾点。

1 矛盾点介绍

1.1 分区角度精度较高的光型

图1(a)为模拟的一种精度较高的光型图，相邻的两分区之间叠加0.3°@0.5 lx，单个分区角度为2.6°@0.5 lx，叠加分区较少，在叠加区域外的光型互不影响。此种光型的优势为当ADB功能启动时，单个独立分区的占比为70%，此时只关闭其中一个分区，暗区角度为1.4°；当车辆跨越其中两个相邻分区的叠加区域时，此时关闭其中两个，暗区角度为3.4°，故当前方车辆在识别角度小于等于1.4°时，则暗区的角度为1.4°或3.4°；当前方车辆在识别角度小于等于2.8°时，则暗区的角度为3.4°或5.4°，以此类推，与设计角度相差较小，尤其出现多个车辆时，由于分区之间互不影响，故在非叠加区域的暗区也互不影响，可近似等于1.4°×C(车辆数)，并且当单个分区角度越大时，所产生暗区的角度相差相对也就越小，但单个暗区的角度则会增大；而此种光型明显的缺陷如图1(b)所示，由于叠加区域较少，故整体光型在叠加区域部分则会产生相对的“暗缝”，整体光型水平H-H线上的光强分布如图2所示，产生峰值差较大的波浪状。

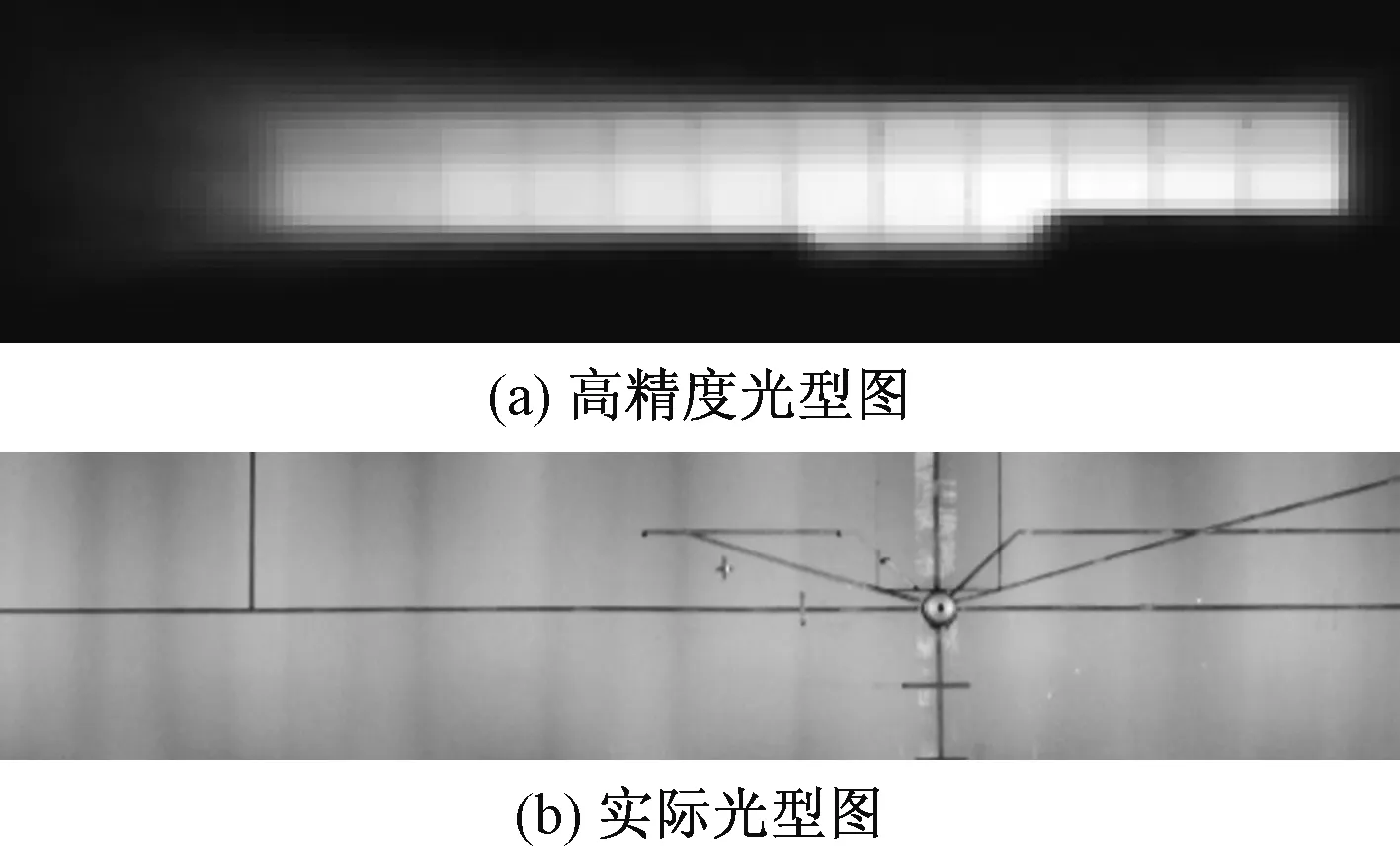
图1 光型图Fig.1 Lightpattern

图2 光强分布图Fig.2 Light intensity distribution

1.2 整体光型较均匀的光型

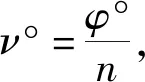
图3 整体光型均匀的光型图Fig.3 Homogeneous light pattern

此光学方案由于每个分区是由多个光型叠加而成，不会形成明显的明暗边界，整体光型较为均匀，且由于“n排”光型进行叠加形成的分区，故总分区数量要比颗粒数量多n个；并且当光型关闭一个分区时，由于关闭的为n颗颗粒，故产生的光型如图4(a)所示，暗区边界梯度较小，过渡均匀；但也正是由于分区由多个光型共同叠加形成，因此当一个光学分区关闭时，左右两侧相邻(n-1)个分区都会受到影响，当出现两个及以上并且相对角度较大的状况时，整个光型变化则会成倍的变化，如图4(b)所示。

图4 暗区光强图Fig.4 Light intensity distribution in dark segment

当车辆前方出现k个需要关闭的防眩目点时，则此光型关闭的分区φ°≤ν°+k×(n-1)ν°，故成比例增加暗区角度。图5(a)为整体光型水平H-H线上的光强分布，基本无峰值的差距；图5(b)为产生一个暗区时整体光型在H-H线上的光强分布，明暗过渡较为均匀；图5(c)为产生两个暗区时整体光型在水平H-H线上的光强分布，暗区较大。

图5 H-H线上的光强分布图Fig.5 Light intensity distribution at H-H line

2 逆向设计理论

从均匀ADB照度分布作为目标开始，采用逆向设计计算ADB分区的光型，X和Y分别是ADB照射的水平角度和垂直角度范围，且照射范围内(x,y)处的光强用E(x,y)表示。

2.1 单排光型设计

由于是单排光型，故在叠加时只考虑X方向的叠加即可，令Y=y，则在此平面上的光强分布E(X,y)，如图6所示。

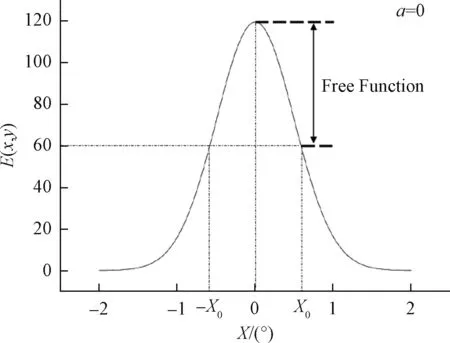
图6 单个分区平面光强分布图Fig.6 2D light intensity distribution map of one segment

1)每个分区光型相同。每个分区光型相同，若边界叠加、过渡均匀，则需满足

E(X0,y)=E(-X0,y)=0.5×Emax

(1)

E(X,y)+E(-X-(b-2×(X-a)),y)=

Emax(X≥a)

(2)

E(X,y)=E(-X,y)

(3)

其中b为单侧叠加角度，a为单个光型存在Emax值的单侧边界。

故整个光型在叠加区域X∈(a,a+b)、X∈(-a-b,-a)中，只存在一个自由函数E(X,y)，满足

a≤X≤a+b/2

(5)

即在整体光型设计时，除均等的最大值外，边界只需给出一个自由函数即可。

现构造一个自由函数，图7所示为任意一个光型的水平H-H线上的光强分布图，其中Emax及单个光型展宽2×(a+b)为光学设计时设定，每个光型间的中心距则为2×a+b，令

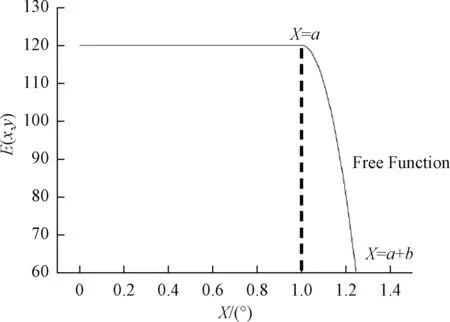
图7 自由函数Fig.7 Freefunction

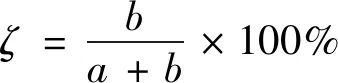
(6)

ζ定义为光型之间的影响程度，ζ值越小时则光型之间影响程度越小，此值在设计时应当考虑。当E(X,t)=-K×(X-a)2+Emax，X∈[a,a+b/2]时，进行逆向设计。

在Y方向上，中心区域满足

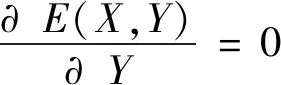
(7)

由于为单排分布，故在Y方向的边界上无需满足与X方向上的一致性。

当自由函数设计完成后，整个光型函数则如图8所示。E(X,y)=E(1)+E(2)为设计自由函数，根据式(1)～式(4)及

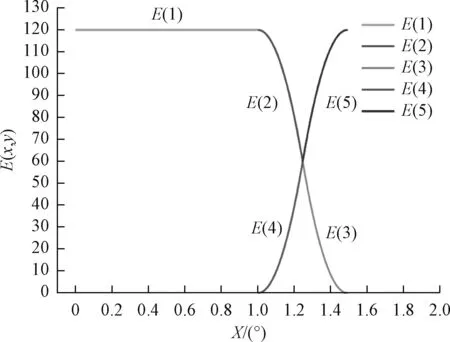
图8 光型函数Fig.8 Optical type function

E(2)=-K×(X-a)2+Emax，X∈[a,a+b/2]

(8)

可得

E(3)=K×(X-a-b)2，X∈[a+b/2,a+b]

(9)

E(4)=K×(X-a)2，X∈[a,a+b/2]

(10)

E(5)=-K×(X-a-b)2+Emax，

X∈[a+b/2,a+b]

(11)

叠加后，X∈[a,a+b/2]时，

E(X,y)=E(2)+E(4)=Emax

(12)

X∈[a+b/2,a+b]时，

E(X,y)=E(3)+E(5)=Emax

(13)

故此时叠加光型与为未叠加部分的光强保持一致。图9(a)为正向模拟结果，图9(b)为相对应分区逆向的模拟结果，可见对整体光型均匀性提升较高。

图9 正向模拟和逆向模拟的光型对比Fig.9 Optical comparison of the forward and reverse simulation result

2)每个分区光型不同。在实际设计过程中，由于对ADB整体光型的需求及节能减排的目的，且考虑实用性，ADB每个分区的光型做成不相同的光型，亮度值从中心向两侧逐渐降低，故从此角度出发同样进行逆向设计，避免叠加时的矛盾点。从整体光型出发，整体光型在H-H线上的光强图如图10所示。

图10 整体光型光强分布图Fig.10 Overall light intensity distribution map

光型左侧斜率：k1=tanα

(14)

右侧斜率：k2=tanβ

(15)

中间部分：E(X,y)=Emax

(16)

此三个数值为设计时确认。在单个分区光型光型设计时，左侧第n个光型中心亮度(定义为Enmax)与单个分区所处分区角度相关：

Enmax=E1max+k1×(Xn-X1)

(17)

故两个相邻分区之间的中心亮度差值为

En+1max-Enmax=k1×(Xn+1-Xn)=k1×(2×a+b)

(18)

故在叠加时进行此两光强光型之间的叠加设计。

在单个光型均匀叠加的基础上进行峰值更改，不变量为叠加区域b，故增加后的中值E(a+b/2，y)位置不变，如图11所示。

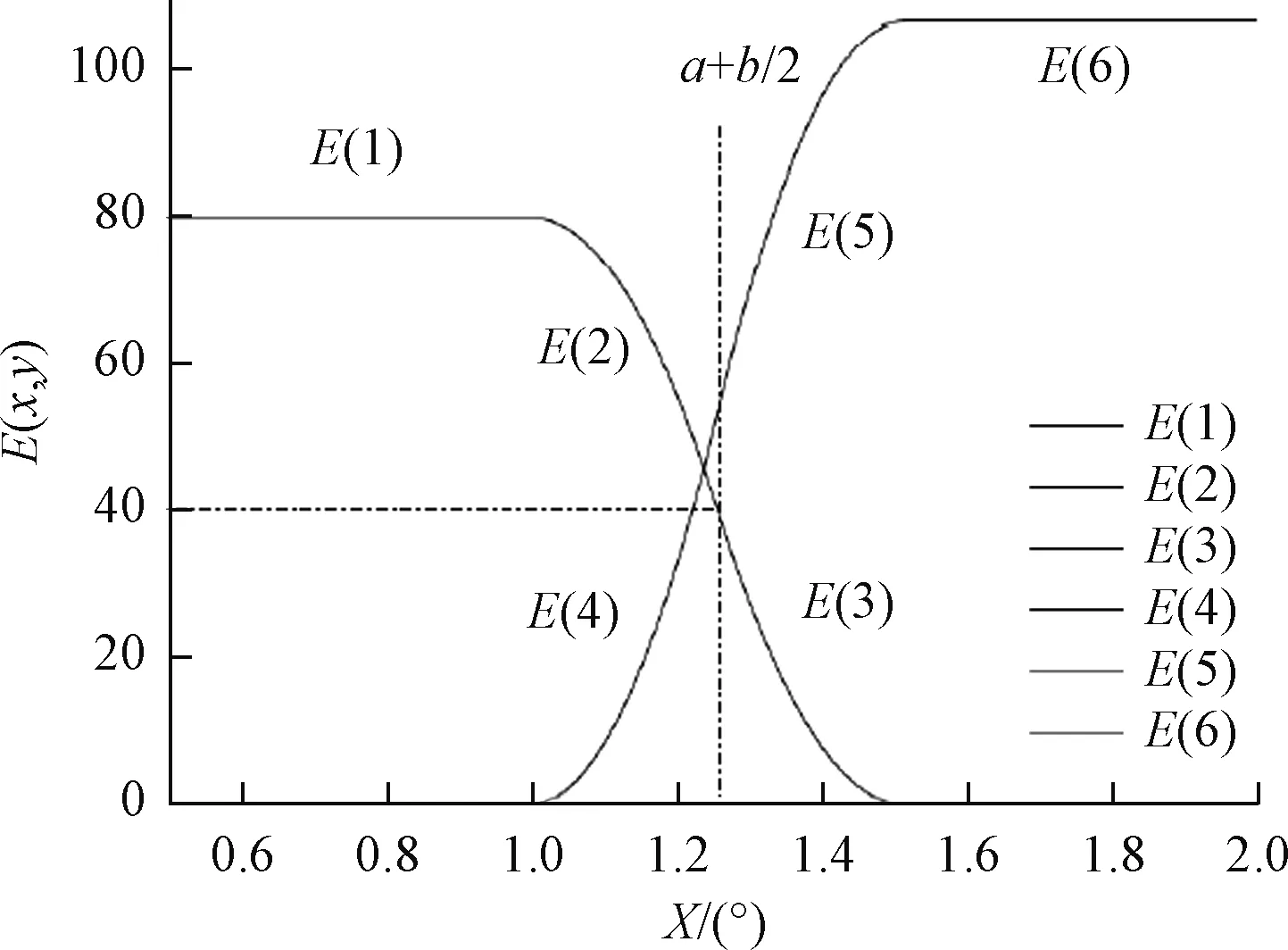
图11 叠加部分光强图Fig.11 Light intensity distribution of the superimposed part

其中：E(6)-E(1)=k1×(2×a+b)

(19)

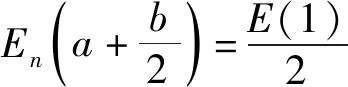
(20)

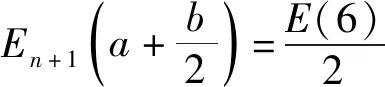
(21)

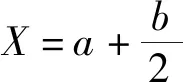
故在E(1)～E(6)叠加区域中，光强叠加从a到a+b的中点为平均光强。

假设

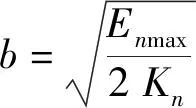
(23)

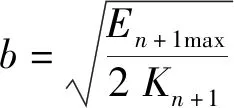
(24)

故E(3)=Kn×(X-a-b)2，X∈(a+b/2,a+b)

(25)

E(4)=Kn+1×(X-a)2，X∈(a,a+b/2)

(26)

叠加区域：

E(7)=E(2)+E(4)=Enmax+(Kn+1-Kn)×(X-a)2，X∈(a,a+b/2)

(27)

E(8)=E(3)+E(5)=En+1max+(Kn-Kn+1)×(X-a-b)2=En+1max-(Kn+1-Kn)×(X-a-b)2，X∈(a+b/2,a+b)

(28)

(29)

故Kn、Kn+1只与Enmax和E(n+1)max相关，与其他变量无关。

综上，此种光型的叠加区域均匀过渡且连续，如图12所示。

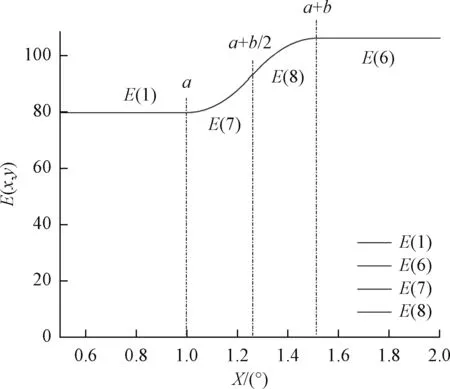
图12 叠加后光强Fig.12 Light intensity distribution after superposition

同理，在整体光型的右侧同样以此进行设计，区别为Enmax值。

2.2 多排光型设计

多排光型设计时，除上述的X方向的叠加需均匀外，同时也需要对Y方向的颗粒叠加进行与X方向相同的逆向叠加方式设计，整体光型则在X、Y双方向上叠加都较为均匀。

针对逆向多排光型设计理论，当设计完成后对整体光型需进行二维均匀性评判，评判方法如下：

假设ADB整体光型在Y=y下的光强函数为E(X，y)，在模拟结果中转化为点数据，每0.1°为一点，共X×Y=n×m个点，形成相对应的矩阵，横向为X，纵向为Y，对应的光强为Exy，此点对应设计值为E(x,y)。

故

(30)

整个Y方向上离散量的平均值为

(31)

当σ(X,Y)值越小时，其与理论值越接近，整体光型也就越均匀。

3 结束语

逆向设计理论在ADB设计的过程中很好地解决了暗区角度与整体光型均匀性之间的矛盾，使得ADB各个分区从随机型设计变成理论型设计，在实现ADB功能的前提下，更好地兼顾了远光的照明效果。在汽车向自动化驾驶发展的背景下，L1～L4级自动驾驶是条必经之路，人车交互将成为趋势，ADB也会随之出现更多的驾驶模式，以帮助驾驶者在夜间更好地驾驶车辆。