基于蝙蝠算法的花粉算法改进
第五杨萌, 贺兴时
(西安工程大学理学院,西安 710600)
花粉算法(Flower Pollination Algorithm,FPA)是英国剑桥大学学者Yang[1]提出的模拟花授粉的新型元启发算法. 该算法所用参数少、易编码,算法中的Lévy飞行机制[2]使得算法搜索路径更优等特点,已广泛应用到经济、管理、军事、科学和工程设计等[3-4]领域的优化问题.
近年来,国内外学者为了提高花粉算法的全局搜索能力和收敛速度,对该算法进行大量研究. 在改进收敛速度方面,高昂等[5]通过种群所有个体信息的交流协作、逐维比较和更新当前迭代产生的最优解,从而加快算法收敛速度;李前等[6]改进步长因子,同时在迭代过程中加入差分进化,提高算法寻优能力;肖辉辉等[7]提出了基于单纯形法和自适应步长的花粉算法,该算法利用单纯形法提高局部搜索能力,通过自适应步长提高收敛速度. 上述几种改进虽然使算法能很快收敛,但是收敛精度较低. 在全局搜索能力改进方面,张新明等[8]将共享机制的小生境策略融合到花粉算法中,增强算法跳出局部最优的能力;吴文斌等[9]通过在较优位置引入遗传算法[10]的改进交叉和变异策略,增强了全局搜索能力;乔现伟等[11]通过立方映射产生的混沌[12]序列,初始化花粉种群,增强了算法的全局搜索能力;卞京红等[13]提出基于萤火虫算法的自适应花粉算法,改进了花粉算法初始种群的质量. 这4 种改进方法虽然提高了算法的寻优精度,但是收敛速度一般.
为了同时提高花粉算法的收敛速度和收敛精度,本文提出一种基于蝙蝠算法(Bat Algorithm,BA)的改进花粉算法(BA-FPA),因为蝙蝠算法[14]通过随机飞行在最优解附近会产生局部的新解,用其初始化[15-16]花粉配子,可以改进花粉算法收敛性能,仿真实验结果证明改进后的BA-FPA 收敛速度和收敛精度都优于基本BA和FPA.
1 算法改进
1.1 花粉算法(FPA)
基础的花粉算法包括自花授粉过程和交叉授粉过程.
交叉授粉即全局授粉过程,

1.2 蝙蝠算法(BA)

在局部搜索中,如果蝙蝠个体选择了一个最优解,那么将在此最优解附近随机生成一个新解:
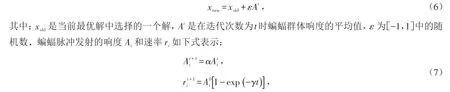
其中:α 和γ 是常数,并且有:0<α <1,0<γ .蝙蝠算法步骤:
Step 1:种群初始化,即蝙蝠以随机方式在D维空间中扩散分布一组初始解. 最大脉冲音量A0,最大脉冲率r0,搜索脉冲频率范围[ ]fmin,fmax,音量的衰减系数α,搜索频率的增强系数γ,最大迭代次数iter_max.
Step 2:随机初始化蝙蝠的位置xi,并根据适应度值的优劣找到当前最优解x*.
Step 3:蝙蝠的搜索脉冲频率、速度和位置分别按照公式(3)~(5)进行更新.
Step 4:随机生成[0,1]间的随机数rand,如果rand>r,则对当前最优解进行随机扰动,按照公式(6)产生一个新解.
Step 5:随机生成[0,1]间的随机数rand,如果rand<Ai且f(xi)<f(x*),则接受Step 4产生的新解,然后按公式(7)进行更新.
Step 6:对所有蝙蝠的适应度值进行排序,找出当前的最优解和最优值.
Step 7:重复Step 2~Step 5直至满足设定的最大迭代次数.
Step 8:输出全局最优值和最优解.
1.3 基于蝙蝠算法的花粉算法(BA-FPA)
蝙蝠算法通过随机飞行在最优解附近产生局部的新解,能使花粉算法在初始时刻有较大的搜索范围,加强了算法整体的局部搜索能力. 因此用蝙蝠算法优化花粉算法的初值,来改进花粉算法初始化种群的质量.
BA-FPA算法步骤:
Step 1:用蝙蝠算法初始化花粉配子.
Step 2:定义一个转移概率p,最大迭代次数N.
Step 3:对于种群中所有的n个花粉配子进行授粉:随机产生一个随机数rand,若rand<p,则进行全局授粉;否则,进行局部授粉. 评价新解,若新解更好,则更新种群. 找到当前的最优解.
Step 4:若算法停止准则满足,则停止;否则转入Step3.
Step 5:输出全局最优值,算法结束.
2 仿真与结果分析
2.1 测试函数及实验参数设置
仿真实验使用Matlab 2017版运行,本文从Benchmarks测试函数[17]中选取6个典型的函数进行测试. 如表1所示,其中Egg creat函数、Sphere函数和Griewank函数为多峰函数,其他为单峰函数.
FPA算法种群规模n=20,转换概率p=0.8. BA算法种群规模n=10,响度A=0.25,脉冲发射率r=0.5.

表1 测试函数Tab.1 Test functions
2.2 实验结果及分析
图1~图6分别是BA-FPA算法、标准BA算法和FPA算法在6种测试函数上的寻优曲线图,可直观看出3种算法的收敛性能. 从图1和图2可以看出,对于2维的Cube和Egg creat函数,3种算法都能成功收敛,同样迭代次数下,BA-FPA的收敛速度明显快于标准BA和FPA的收敛速度;从图3可以看出,对于3维的Rosenbrock函数,迭代次数为1000次时,BA-FPA的收敛速度明显快于标准BA和FPA的收敛速度,BA-FPA能快速收敛到最优值,BA还不能收敛到最优值. 从图4~图6看出,随维数增加,BA-FPA 的收敛性能明显好于标准BA和FPA的收敛性能.
为了检验算法寻优的稳定性,分别用BA-FPA算法、标准BA算法和FPA算法对每个测试函数优化50次,统计结果如表2所示.

图1 Cube函数寻优曲线Fig.1 Optimization curves of Cube function

图2 Eggcreat函数寻优曲线Fig.2 Optimization curves of Eggcreat function
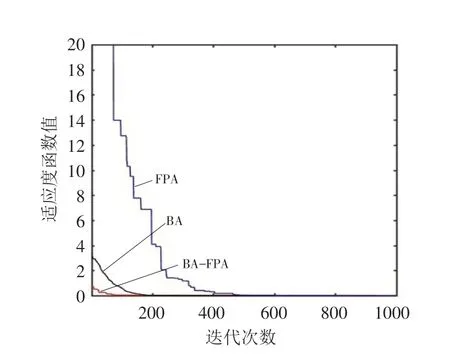
图3 Rosenbrock函数寻优曲线Fig.3 Optimization curves of Rosenbrock function
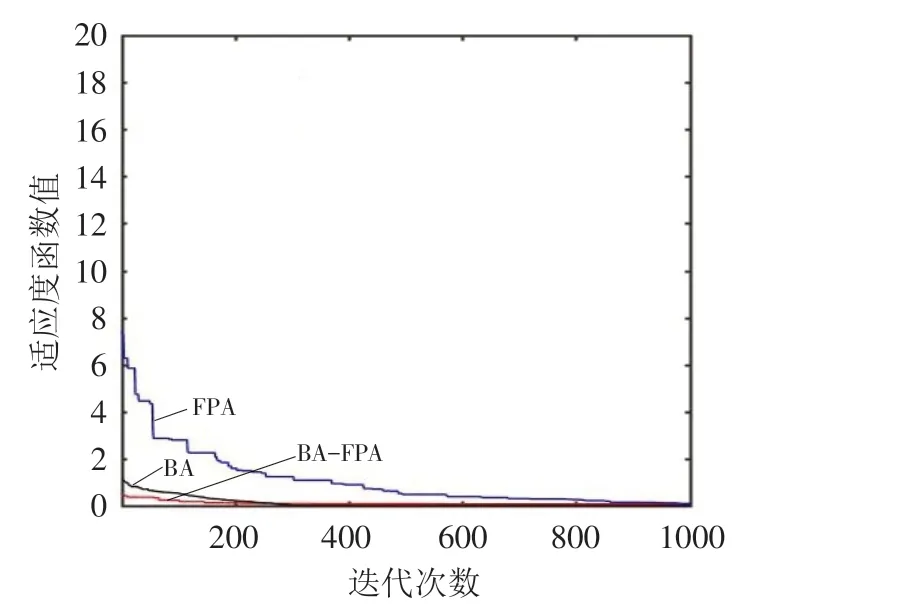
图4 Sphere函数寻优曲线Fig.4 Optimization curves of Sphere function

图5 Griewank函数寻优曲线Fig.5 Optimization curves of Griewank function
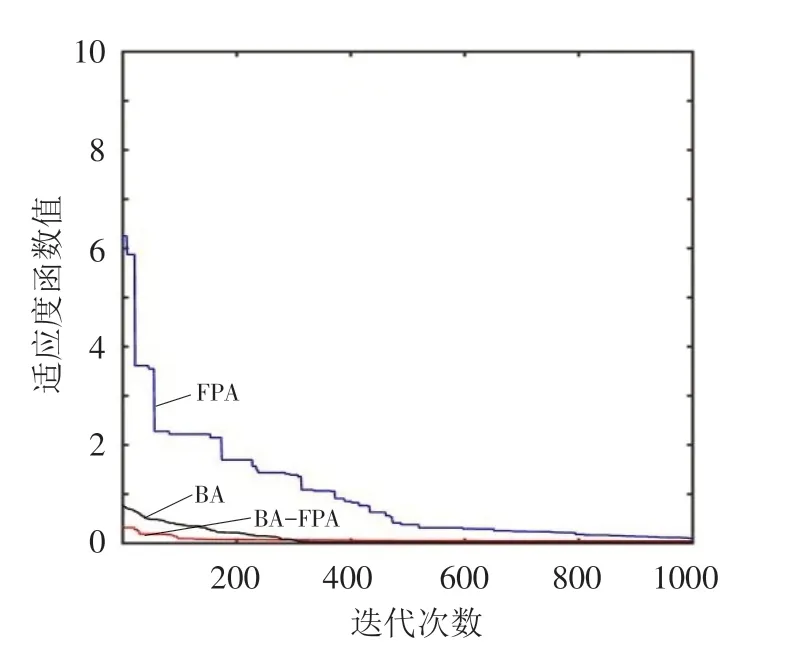
图6 Schwefel 2.21函数收敛曲线Fig.6 Optimization curves of Schwefel 2.21 function
从表2 中仿真实验结果可以看出,BA-FPA 算法运行得出的最小值、最大值和均值比标准BA 算法和FPA算法在收敛精度上有较大提升. 而且测试函数有不同模态(unimodal,multimodal),还有不同维数(2维、3维和10维). 因此,改进后的BA-FPA算法收敛性能(收敛速度和收敛精度)比标准BA算法和FPA算法有较大提升.

表2 BA-FPA、BA和FPA算法性能比较Tab.2 Performance comparison among BA-FPA,BA and FPA
3 结语
本研究将蝙蝠算法引入花粉算法来优化花粉配子的初始位置,建立基于蝙蝠算法的花粉改进算法. 通过任意选取6个基准测试函数对算法进行性能测试,结果表明改进后的BA-FPA算法比标准的BA和FPA具有更快的收敛速度和更高的收敛精度.

