考虑干湿循环的大理岩统计损伤本构模型
王 辉, 王 伟, 朱鹏辉, 李 尧, 刘志航
(1.河海大学岩土力学与堤坝工程教育部重点实验室,南京 210024; 2.河海大学土木与交通学院岩土所,南京 210024;3.中交上海航道勘察设计研究院有限公司,上海 200120)
岩石在不同的位置裂隙分布具有很大的差别,而岩石的干湿循环试验结果与岩石的裂隙发育情况具有很大的关联. 因此本文着重以岩石的裂隙微元体的发育情况来定义岩石的劣化损伤模型. 近年来,研究人员在岩石劣化损伤模型研究方面取得十分丰富的成果. 曹文贵[1]提出了强度破坏准则来表示微元强度,发现了岩石在一定应力下产生的损伤应用微元强度能够更好地描述. 张梦成等[2]在连续损伤原理的基础上引入最小耗能原理,并应用各向同性假定构建损伤本构模型. 冯晓伟等[3]对水化学腐蚀作用砂岩三轴蠕变实验数据进行研究,运用广义Kelvin模型构建了砂岩的损伤流变本构模型. 石崇[4]引入虎克-布朗准则、郑志[5]引入Mogi-Coulomb准则、田振元[6]引入拉德-邓肯破坏准则等不同的破坏准则描述岩石的微元强度,都说明应用微元强度描述岩石的劣化具有一定的优越性. 张慧梅等[7]基于Weibull分布角度,通过冻融与荷载耦合作用建立了岩石损伤模型,考虑了损伤特性等多因素作用,验证了损伤本构模型对试验结果较好的拟合效果.
水电站周期性的蓄水与排水等情况会造成库岸边坡的干湿循环交替,其劣化机理复杂. 目前,研究人员就干湿循环造成的岩石劣化损伤进行了研究. 谢学斌[8]基于砂岩的单轴压缩与干湿循环耦合作用的劣化机理,证实砂岩在干湿循环作用下力学性质明显劣化. 傅宴等[9]通过CT扫描的方法对干湿循环下砂岩进行研究,证实在干湿循环下其内部胶结物质溶蚀,松散颗粒增多,孔隙、裂隙也随着增多,强度也相应降低. 姚远[10]统计了泥岩在干湿循环下裂缝面积,证实了在干湿循环下最初几次的干湿循环样品裂缝发育面积最大,并得出岩石强度损失是由于样品裂缝快速发育的结果. 这些研究大多集中于研究砂岩与泥岩在干湿循环条件下岩石的劣化损伤机理,针对大理岩在干湿循环作用下的损伤本构模型目前还比较缺乏.
本文以锦屏大理岩为研究对象,结合对干湿循环作用下大理岩单轴压缩试验数据,建立考虑干湿循环效应的统计损伤本构模型,描述大理岩干湿循环下的劣化规律,为边坡稳定性设计提供一定依据.
1 损伤本构模型的建立
岩石损伤本构关系模型一直以来是人们普遍关注的问题,研究者利用统计学原理研究损伤,对于岩石的统计损伤本构模型的研究取得了突破性的进展[11-12].
1.1 损伤变量的定义
建立损伤本构模型之前,要先定义损伤变量[13-14]. 本文利用材料的微元体随机分布推导损伤本构方程.运用统计损伤理论来建立损伤本构模型,本文以统计微元体的数目来定义损伤变量:

式中:D为损伤变量;ND发生破坏的微元体数目;N为假定的微元体总数目. 微元体在岩石中不同的位置具有不同的分布,但是通过分析可以得出其规律.
分析微元体分布情况对损伤本构模型的建立起到的关键作用. 岩石材料的内部充满孔隙、裂隙、节理,且是随机分布,其对应的微元强度也是随机分布. 本文假设岩石微元强度服从Weibull分布[15],定义微元体强度F分布服从概率密度函数,表达式为:

式中:m,F0为Weibull分布函数参数;F为岩石微元强度.
微元强度F的概率密度函数确定后,任意应力区间出现的破坏微元体数目则可以用NP(x)dx 来表示,破坏微元体数目对应力区间积分得到发生破坏时微元体数目为:

将式(3)带入式(1),可以得到微元强度与损伤变量D的关系公式为:

1.2 考虑干湿循环作用的大理岩统计损伤本构模型建立
由于D-P破坏准则在岩石破坏中考虑中主应力的影响,适用性较广,参数形式简单,对比于其他的破坏准则有其独特的优势,更加精确地反映岩石的受力情况,所以本文采用D-P破坏准则表达岩石的微元强度准则,基于D-P破坏准则建立度量微元强度[16]表达式为:


2 模型参数辨识与模型验证
2.1 岩石损伤本构模型参数辨识
本文确定Weibull分布函数参数方法采用线性拟合法[19]. 线性拟合法计算的函数参数物理意义不太明确,但是计算过程比较简单,计算过程中不容易出错,一般计算Weibull分布函数参数采用这种方法.
为了确定Weibull分布函数参数,将式(17)、(18)、(19)、(24)带入式(4),可得到
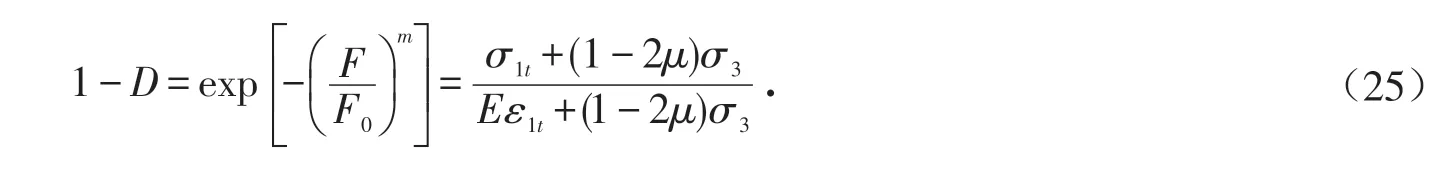
对表达式同时取对数:

对表达式再次取对数,其表达式为:

对其进行线性化处理,令:
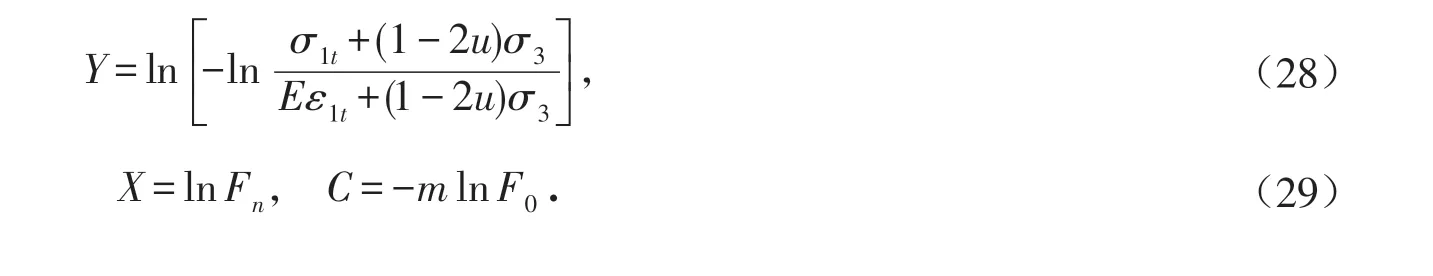
则可以将其转化为线性表达式:

由式(30)可知,其中Weibull函数参数m决定线性曲线的斜率,-m ln F0决定线性曲线的截距,将不同干湿循环次数下数据带入表达式(30)中,通过线性方法可以求Weibull分布函数参数m、F0.
2.2 岩石损伤本构模型的验证
对本文建立大理岩统计损伤本构模型进行验证,结合引用王伟[18]等大理岩干湿循环力学特性试验研究试验数据验证模型,为了便于数据验证,可以考虑单轴试验下数据对统计损伤本构模型进行验证,在单轴条件下,试验围压数值σ2=σ3=0,将其带入式(24),则单轴条件下大理岩干湿循环损伤本构模型表达式为:

为了将统计损伤本构模型与试验所记录数据结合,将统计损伤本构方程转化为与偏应力σ1t有关的表达式,则大理岩干湿循环条件下统计损伤本构模型的偏应力σ1t表达形式为:

采用线性拟合法来确定Weibull分布参数m、F0. 在单轴试验中,对0次、12次、28次、44次干湿循环的试验数据来进行计算,可以求得Weibull函数参数m、F0,如表1所示.

表1 各循环次数下参数m,F0与阶段损伤率ΔDs值Tab.1 Parameters m,F0 and stage damage rate ΔDs under each cycle number
通过对不同循环次数下m、F0与阶段损伤率ΔDs变化趋势研究发现,Weibull分布函数参数m在不同循环次数下变化较小,可以视为一个常数,取其平均值m0来替代m在不同循环次数下的取值. F0在不同干湿循环次数下变化较大,对于不同干湿循环次数下F0取值要分不同的情况. 同时,m、F0、ΔDs在不同干湿循环条件下具有相同变化趋势,即可认为m、F0共同决定了岩石损伤速率.
引用王伟等[18]大理岩干湿循环力学特性试验研究单轴试验数据,可以得到模型参数如表2所示.

表2 本构模型参数Tab.2 Constitutive model parameters
将模型参数带入大理岩统计损伤本构模型(26)式,可以得到在不同的干湿循环条件下大理岩统计损伤本构模型理论曲线,将其与试验曲线进行对比分析,如图1~图4所示.

图1 干湿循环0次Fig.1 Dry-wet cycles of 0 times

图2 干湿循环12次Fig.2 Dry-wet cycles of 12 times

图3 干湿循环28次Fig.3 Dry-wet cycles of 28 times

图4 干湿循环44次Fig.4 Dry-wet cycles of 44 times
由图1可知,对不同干湿循环条件理论曲线与试验曲线对比可以看出,在岩石破坏的弹性阶段,统计损伤本构模型曲线能够较好地拟合试验数据,但是在塑形阶段,理论曲线与试验数据曲线具有较大的差异,统计损伤本构模型对曲线的拟合效果不太理想.
3 结论
1)文章通过大理岩干湿循环作用下0次、12次、28次、44次劣化现象的研究,通过大理岩的微元体强度服从Weibull分布函数,并且结合连续损伤理论,Lemaitre 应变等效假说和虎克定律,运用了统计学的方法,提出了考虑干湿循环效应大理岩的统计损伤本构模型.
2)通过对比在不同干湿循环次数下,Weibull 函数参数m、F0与阶段损伤率ΔDs变化趋势发现,m变小较小,可视为一个常数,F0在不同干湿循环次数下变化幅度较大,对不同干湿循环次数下要取不同的数据进行拟合,且m、F0与阶段损伤率ΔDs具有相同的变化趋势,可以认为m、F0是反映岩石在不同干湿循环条件下岩石损伤速率的参数.
3)依据统计损伤本构模型所得到的理论值与不同干湿循环作用下大理岩试验数据进行拟合,通过对拟合曲线进行研究,发现在不同的干湿循环次数下,损伤本构模型理论曲线在大理岩弹性变形阶段能够较好地拟合试验数据,但是在塑形变形阶段,不能达到理想的拟合效果.

