上行与下行人腿膝部受力问题分析

卢冠辰

(洛阳市第一高级中学，河南 洛阳 471000)

0 引言

人类下肢的结构十分精密，膝部是下肢的一个重要支撑作用集中点[2,4,7,8]。它除了承载由人体自重而产生的静态重力作用外，运动过程中的惯性力也由膝部承担。事实上，国际上对于腿部运动的研究是相当深入的，重视加之合理的下肢运动方式，有利于减少膝部受损情况发生的几率。虽然相关讨论众多，但这些讨论大多基于对行走式机器人相关关键要素的分析，对于腿部运动对应的人身基础受力问题，现有分析并不足够充分和深入。从现存模型上看，尽管整体机器的多连杆运动经典模型，可被应用于下肢运动研究及规律分析，然而，对于人体的下肢多样化的运动方式及相关运动环境因素、或对于人本身面临的下肢运动问题的分析及判断等，在实际人腿运动受力方面，较为复杂的研究模型就显得并不方便，也并不容易得到膝部具体受力与运动方式上的明确关联。显然，提出一种简化的易于理解的下肢运动模型，并具体分析人腿膝部受力的量化问题，一方面可以得出明确的腿部运动与腿部受力间的数量关系，同时，对普及或推动下肢健康运动的认识也会形成有益的讨论，而所有这些对于引发初学者的步行式机器人的入门研究也会产生一定的促进作用[1,6,9-11]。因此，本文以上下行腿部运动为研究对象进行模型简构，并作受力分析，以期为腿部运动的受力关系及相应的膝部关节相关防护方面进行有意义的讨论。(参见图1(b))

图1机器人(a左)来自网络(BU robot)；机器人(a右)，是已被Google的“Atlas”双足机器人； (b)腿部关节简图及膝部具体结构

腿部支撑身体重力，人体通过腿部常见的肢体运动来实现身体的物理迁移。基于现代化的工具或设备使得目前人体的移动方式主要建立在滚动的运动形式上，但肢体的运动方式仍然无法被全面替代。一方面，人们出于关注健身方面问题的需要，有益的下肢运动是人们关注的热点，另一方面，连接杆式运动在智能化社会进程发端之初也是科学家十分关注的研究课题[1,2,5,6,9-11]。(如下图1(a)普通滚动行走机械人及行走下肢行拟人行走机械人)。

1 建模及过程分析

作为人腿行走的主要方式，上行与下行地位的重要性是显而易见的。由于上下楼过程步长以及步高(或步深)有显著的周期性(见图2)，为了问题研究的方便，我们将腿部的上下行行为简化为常见的上下楼过程，并以此为基础进行腿部模型构建和简化分析。

图2 上下楼梯平衡过程真人模拟：(a)(b)上楼梯准备及模拟启动； (c)(d)下楼梯准备及模拟启动

在上楼过程中，前腿起人体主支撑作用，后腿辅助身体迁移至上级台阶，当前腿直立时，原后腿移至上级台阶并弯曲，此时，身体重心切换迁移至新的前腿，并完成后面腿部的直立，直到最先启动的腿再度移动至上一台阶并发生弯曲，如此完成一个上行周期。在下楼过程中，后腿起人体主支撑作用，前腿辅助并移至下一台阶。当后腿直立时，身体重心切换移至前腿，前腿发生弯曲后直立，直到最初的后腿再度移动至下一台阶并发生弯曲，如此完成一个下行周期(见图3)。

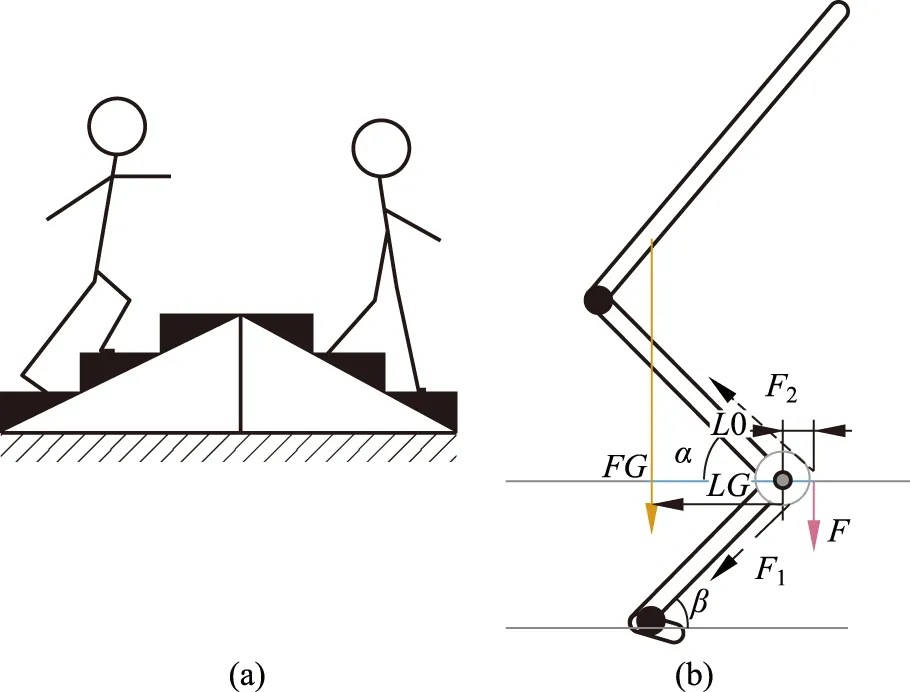
图3(a) 上下行楼梯的简图; (b) 受力腿的弯曲及其受力图示

从以上实际过程分析及图示分解可以看出，上下楼梯过程是身体重心在腿部支撑作用下的曲腿直立过程，膝部是整个人体上下行的受力核心。假如在每一个移动过程中，人体均处于受力平衡或平衡运动状态，便可以方便地将这一曲腿直立的受力过程进行简化。如图3(b)所示，为了保持身体平衡，身体的重心落于支撑曲腿的足部，而腿部关节的角度在可调范围变化，其过程均满足重心落于支撑腿足部的基本规律。有了这个基本前提，同时考虑忽略腿部自重，视腿部为轻质刚性连杆，便可简构此过程的静态及平衡运动模型，并在此基础上对承力腿的受力进行过程分析。

1.1 静态平衡上下楼受力分析

1.1.1 上楼梯的平衡受力分析

如图4所示，依照人体重心通过提供身体支撑的前腿足部，腿部的受力处于平衡。此时，以膝关节中心部位为实际支点，大腿所受外力处于力矩平衡状态，因此可得如下关系：

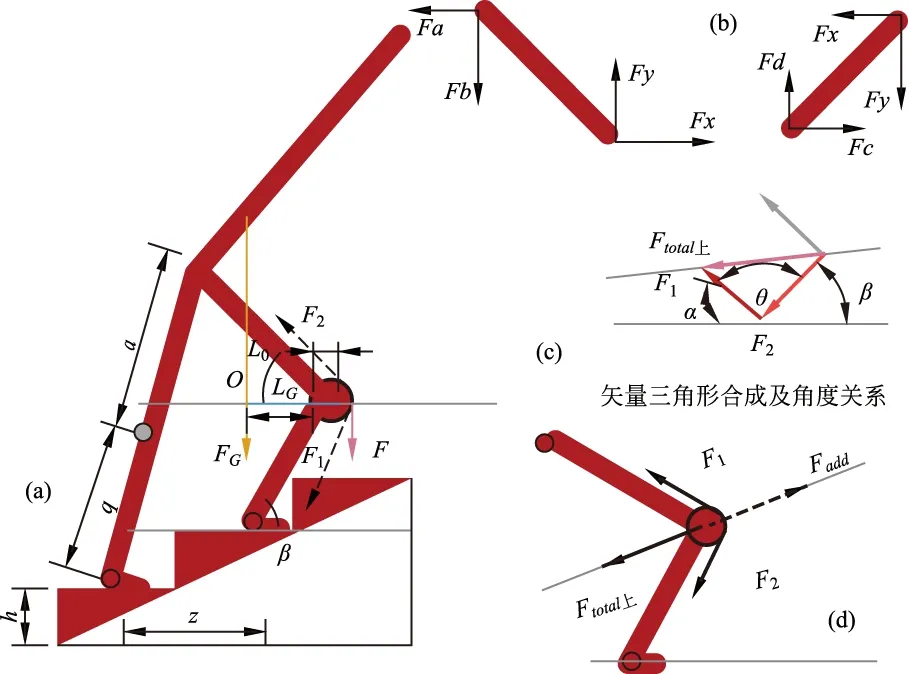
图4(a) 上楼梯时运动模型(含相关参数); (b) 大腿、小腿分解受力; (c) 膝部受力合成； (d) 弱化膝部受力的补充力图

(1)

如图4中，F1为通过膝关节前端的髌骨由肌肉肌腱一体产生的沿大腿向上的拉力，F2为通过膝关节前端的髌骨由肌肉肌腱一体产生的沿小腿向下的拉力。其中作用于膝关节的切线竖直向下的力为F，F到膝关节中心的距离为L0，由于自身重力而产物的逆时针力矩为由人体在大腿上产生的力FG与力臂长LG的积，b为小腿长度，β为小腿与水平地面的夹角，M为人自身的质量，g为重加速度。因此可得：

(2)

显然，此时，沿膝关节前方切线所受竖直向下的力由人体自重Mg、小腿长度b、小腿与水平地面夹角β、及人体重力方向到膝关节中心的距离L0共同决定。

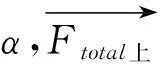
根据力的三角形法则(图4-Ⅲ)及余弦定律，可得如下方程：

结合方程(1)可得：

显然，Mg、b、L0为常量，为了分析膝部受力的变化情况，可将膝部的受力作以下简化：

(3)

其中ε为由Mg、b、及L0规定的常量。

由此可见，上楼梯时，膝部受力对于特定的人而言(小腿长b及体重Mg一定)，膝部受力主要和小腿与水平地面的夹角β，及大腿与水平台面的夹角α有关。其中夹角β越大，膝部受到拉力越小。根据力的合成法则，而沿膝部髌骨的双向拉力的合力随二力的夹角的增大而减小，而这一合力的夹角θ与α及β的和成负相关的关系，因此，α及β的夹角和越大，膝部的受力越小。同时，设大腿与小腿外延长线的夹角为θ′，其角度的变化是一个容易观察的量，由图5中所示的几何关系，可得到如下角度关系：

图5(a) 重力支撑腿各方向角度关系; (b) 矢量三角形合成及对应角度关系对照图示

而人上行时，受力腿所对应的θ′逐步变小，结合夹角β的变化，依据方程(3)，理论上可得膝部所受合力的变化情况。

上述为理论推导过程，真正要得出腿部的过程受力，还需要进行相应的实际测量。由于图中所标注的夹角α及β随时间变化，为了记录其变化与时间的关系，实验中我们采用了水平录像的方法，将所得影像进行处理，按固定时间间隔选取图像，以作图软件(Coreldraw，亿图等)对所选图像中对应的夹角进行测量，可得如下α及β随时间变化的图形(如图6所示)。由图可知，通常情况下观察者上楼时腿部角度按图6所示发生变化，两种角度的值随时间同步增加，上楼启动阶段，以承重腿开始撑体重为起点，此时相应的两角度均为最小值，这样我们可以结合方程(3)以及表1中实际的腿部骨骼数据，能够比较方便计算出正常情况下一般人群膝部受力大小以及上行时的受力变化情况。

表1 根据我国公布的成人躯干的平均数据,如表所示,确认人体各部分的长度[3]

图6 实测鸿儒小区10#楼上台阶时主支撑体重大小腿与水平面夹角随时间变化图(台阶平均高：156.5.mm台阶平均宽：299.0mm)：■表大腿与水平地面夹角α的度数，•表示小腿与水平地面夹角β的度数

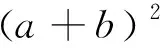
其中，设κ为步长z的比例系数，当在上述观测点测量时，对于同一人及相同楼梯而言，此方程可以进一步简化，设

则可得上楼梯时，α、β两夹角存在下列关系：

(4)

联合上述方程(2)，(3)，(4)，结合腿各部分长度以及人体自重等已知量，便可以十分方便地计算出在静态及平衡受力时膝部的受力情况。(过程见下图7人上楼梯身体重心从双足间切换至与单足垂直同线过程图示)。依据上述结论，可以进行实际情况下的膝部受力计算及极值分析：

图7 上台阶启动初期台阶与腿各部长度及角度关系示意图

1.1.2 下楼梯的平衡受力分析

如图8所示，将人下楼梯的样式做出简图，依照平衡状态下重心通过支撑前腿足部，腿部的受力处于平衡。此时，以膝关节中心部为实际支点，求大腿处力矩平衡方程，可得：

方程中，各物理量所指均与上楼梯相同，因此我们依然可以得到以下方程：

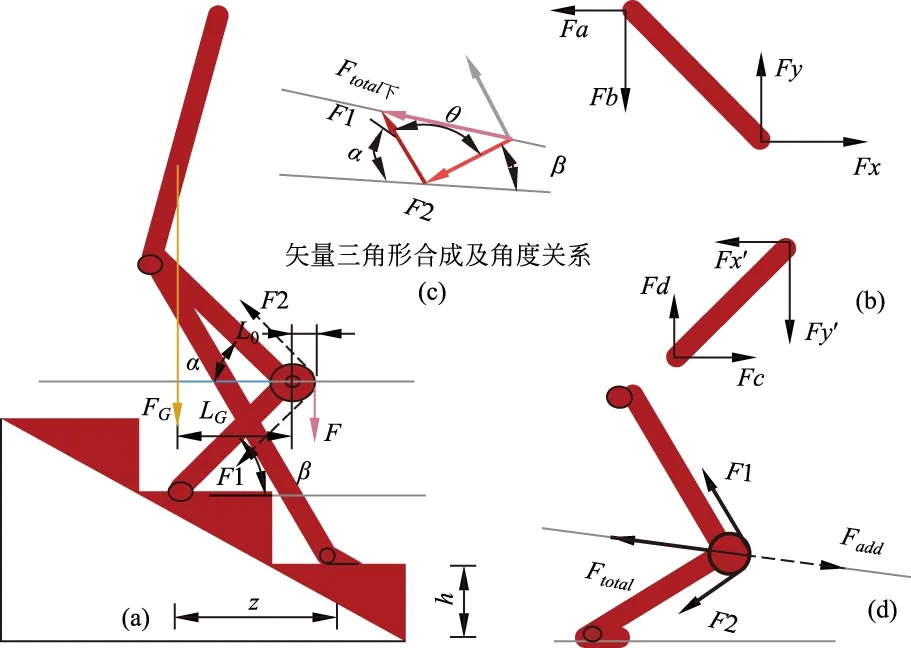
图8(a) 下楼梯时运动模型(含相关参数); (b) 大腿、小腿分解受力; (c) 膝部受力合成; (d) 弱化膝部受力的补充力图示

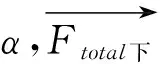
根据力的三角形法则及余弦定律，可得如下方程：

结合方程可得：

(5)

显然，由于Mg、b、L0为常量，故膝部的受力可简化为：

其中ε为由Mg、b、及L0规定的常量。

同时，从图9所示的情况来看，下楼梯也将出现与上楼梯相类似的情况，我们仍然可以得到提供支撑力的大腿与水平面夹角或小腿与足部所在平面间夹角间的关系式：

图9 下楼梯启动初期台阶与腿各部长度及角度关系示意图

从上面讨论的结果，可以得出结论：在参与计算的所有关系量一定的情况下，上楼与下楼腿部膝关节受力情况并无差别。两种情况下，膝关节的受力只与大小腿与水平面的夹角有关。

2 结果与讨论

2.1 实际非平衡条件下的膝关节受力拟合

前面的讨论仅限于静态或受力平衡状态下人腿上下行的受力分析。很显然，现实情况要繁杂的多。为了将模型的应用更接近现实，我们要做进一步讨论。

现实生活及医学证据常常证实，人们在下楼梯时膝部关节受到力要大些。从长期来看，当膝关节受力较大且持久时，造成膝关节损伤的可能性也更大。因此有人认为人们进行腿部运动时应尽量避免较多的下行活动：如上下楼时，要减少下楼运动，而生活中也有“上山容易下山难”的体验。很显然，实践得出的认知从一定程度上与前本文中讨论的结论出现了偏离。这主要与上面讨论模型的成立以静平衡态为前提有关。实际情况下，人在运动过程中，均会出现一定的偏离平衡态的情况，一旦整个上下行过程中出现了不平衡受力情况，相应的人腿上下行过程的受力则要在原来的模型基础之上进行相应的条件叠加，以使其与实际情况相适应。如下图所示，实际条件下，人的上下行过程都伴有一定的加速度，为了让模型合理，我们应在其中引入惯性力。此时，原模型中的方程要发生相应变化：

方程中的μ为在运动中引入的竖直加速度分量，显然，这一条件下，我们将得到一系列新的方程：

此时，我们依照实际角度来考虑上下楼梯时的区别：当下楼梯时，人的运动将伴随着势能转化为动能的过程，而上楼时，这一能量转换过程主要是人体内能转化为人体势能的过程。同样条件下，下楼时身体重心将产生较大的向下惯性力(a′

据上面讨论，上下行过程膝部受力方程如下：

(8)

2.2 减缓膝部受力分析

国际上通常利用脚底缓冲的方式来降低运动中膝部的损伤。例如，一般认为在塑胶材料上进行运动可以有效减少膝部损伤，该方法本质相当于减小了人体的向下惯性力。基于文中模型推导的结果，我们自然也希望本简构模型能在上下行中膝部受力的缓解方面产生作用。

如图10所示，从图中我们发现，膝部所受合力的方向与运动方向大致反向(其具体方向由力的三角形合成法则决定)，如果能在图中对膝部施加一个与此合力Ftotal相反的力Fadd，从理论上讲，可以起到减弱膝部受力的效果。为了得到这样一个力Fadd，设想在大腿与小腿间添加一个弹性物体，当大腿与水平面的夹角α以及小腿与脚部平面间的夹角β较小时，根据前面的结论，此时膝部所受合力也最大，这也是最易造成膝部受力损伤的时候。然而，与此同时，大腿与小腿间添加的弹性物体所受的压缩形变也最大，弹性体可以产生的弹性反作用力也较大，因此，Fadd此时也应最大。两力叠加，即可达到有效减缓膝部受力的作用效果。最终膝部的受力应为：

图10 膝部受力及介入式减缓作用分析

F=Ftotal-Fadd

(9)

3 结论

通过上述有关上下行人腿膝部受力问题量化研究，我们可得到如下结论。

1) 从静态或平衡运动状态上讲，人的上下行过程中，膝部受力和腿与平面的角度、小腿的长度、人的体重、楼梯的高及步长等因素有关。但由于上行与下行过程中对应的各数量因素相同，因此两种情况下膝部受力并无区别；

2) 从上下行的实际情况上看，由于惯性力的存在，使得实际上膝部受力与平衡状态下不同。由于上下行时两种情况人体躯干重心产生不同的加速度，其中下行加速大于上行加速度，因此下行运动时膝部受力要明显大于上行情况。从而用数据说明，人们认为的下行易伤膝的说法成立；

3) 文中模型可以得到上下行运动中膝部受力变化趋势，膝部受力的极值问题也可以依具体情况可以得出。这些数据可为医学、运动学、步行机器人的下肢构建、甚至建筑学中台阶各尺寸的合理设置等，提供有价值的参考借鉴；

4) 基于及缓解膝部受力的观点，我们在腿部简构受力模型中引入了附加力(详见式(9))。从原理上有望成为一种减缓膝关节损伤的便宜方式及有效途径；

5) 最后，文中提到的产生弹力形变的材料设计、选取、组装，以及设置等问题将会成为本课题下一步探索的重要研究内容。