三维空间中由坐标和电势确定匀强电场矢量的矩阵公式

李 力

(重庆市清华中学，重庆 400054)

1 由坐标和电势确定匀强电场矢量的矩阵公式

在三维空间中建立直角坐标系O-xyz，任意三点A,B,C的位矢各为ri=(xi,yi,zi)，其中i=1,2,3。设空间中有匀强电场E=(Ex,Ey,Ez)，测得原点O以及A,B,C的电势分别为φi(i=0,1,2,3)，进而算出此三点到原点O的电势差分别为Ui0(其中i=1,2,3)，则由静电场电场强度与电势梯度之间的关系E=-φ[1]，并注意到匀强电场场强是恒矢量，得

E·ri=-Ui0=U0i=φ0-φi(i=1,2,3)

(1)

可以写出分别沿r1,r2,r3的三个方程为

(2)

如果令矩阵

(3)

那么上面的线性方程组(2)可以写成矩阵方程的形式[2]

RE=U

(4)

如果行列式|R|≠0(几何意义为r1,r2,r3不共面)，由克莱姆法则得方程组(2)的解为

(5)

当然在行列式|R|≠0的条件下，表明存在逆矩阵R-1，那么方程(4)的解可写为

(6)

由上述可知，从这个物理问题建立的数学方程分别是矢量方程形式(1)、线性方程组形式(2)和矩阵方程形式(4)，求解的一般公式中最简明的是矩阵公式(6)。

从上述推导过程还可以看出，在三维空间中确定匀强电场的场强矢量，需要已知不共平面的任意4个点的电势(或相应的3个电势差)。于是不难明白，如果已知匀强电场与某平面平行，则只需已知不共直线的3个点的电势(或相应的2个电势差)，式(2)～式(6)将改写为相应的更容易求解的二维形式，此处不再赘述。

2 几个三维和二维例子

例1已知匀强电场中点A(1,1,1),B(2,1,3),C(0,3,4)的电势分别为10V，17V,24V,而原点电势为3V，坐标轴上单位长度为1m，求场强矢量。

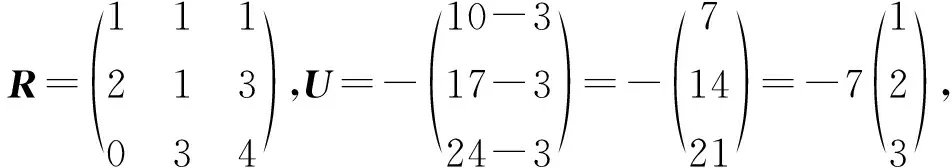
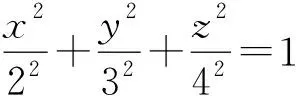
解：不用照套公式，从式(1)可得式(2)形式的方程组为Ex·2=1-3，Ey·3=1-4，Ez·4=1-5，故E=(-1,-1,-1)V/m。

例3一匀强电场的方向平行于xOy平面，平面内a,b,c三点的位置如图1所示，三点的电势分别为10V,17V,26V，求电场强度的大小。

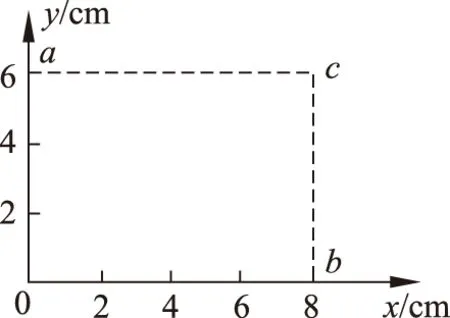
图1 二维问题举例

解：这是2017年全国高考课标Ⅲ卷的第21题，是一个平面问题，通常用寻找等势点的几何方法求解是比较繁琐的[3]。当然可以直接用套用退化后的二维形式解决，这里采用更简洁灵活的解题策略[3]。因为ao//cb且ao=cb，根据匀强电场性质φa-φ0=φc-φb，得φ0=1V，所以

3 结语

本文用线性代数方法，导出三维空间中由电势确定匀强电场场强矢量的矢量形式方程(1)、线性方程组形式(2)和矩阵方程形式(4)，给出了解的一般公式(5)和公式(6)，求解了几例三维问题和二维问题。这一方法无需寻找等电势点和复杂的几何关系，即使当所给位置关系或电势数值比较一般化甚至为一系列已知字母时，也能直接统一、简洁地求出场强矢量，明显优于“通过寻找等电势点再确定等势(面)线及场强方向最后计算场强大小”的几何方法。