航空电连接器力学性能和电学性能仿真

张 彤，郁大照

（海军航空大学，山东烟台264001）

随着机载涉电部附件日益增多，机载涉电部附件的安全平稳运行已经成为飞机健康飞行的重要保证。电连接器是用于实现器件、组件和系统之间电信号和相关控制信号的传输的基础性元件，其性能与功能的优劣对整个系统能否稳定工作影响较大，具有应用的广泛性与功能的不可替代性[1]。

力学性能和电学性能是电连接器最主要的2个性能，是电连接器性能退化的研究重点。电连接器的力学性能和电学性能主要包括插拔作用下的应力应变情况，温度、电流、振动作用时的接触压力、接触电阻变化情况，以及动力学相应特性等。在插拔仿真方面，任万滨等人在研究电连接器微动磨损的失效机理时，以某型电连接器的接触对进行实物建模，提出了基于ABAQUS 的电连接器接触对插拔特性和电特性的有限元仿真分析方法[2]。骆燕燕等人利用ANSYS建立了某型号三针圆形电连接器接触件模型，该型号连接器的插孔为四开槽结构，并对插拔过程进行仿真，分析了接触件结构尺寸变化时，接触压力等参数的变化规律[3]。在振动仿真方面，钟泽南通过ANSYS仿真软件对电连接器进行了振动分析[4]。

对力学和电学性能进行仿真分析，有利于发现不同载荷作用下，电连接器的性能退化趋势。与试验结果进行比较，既能验证仿真的有效性，又能为试验结果提供理论支撑。

1 电连接器力学性能、电学性能理论分析

振动导致的电连接器接触表面机械变形和损坏会影响着电连接器的电性能、安全性能以及机械性能，也是电连接器性能退化的主要诱因之一[5-7]。振动在机载设备上普遍存在，插针与插孔在外界机械振动应力作用下，会发生运动幅度很小的相对运动，这种相对运动会对接触斑点产生各种磨损效应，称之为微动磨损，振动必然会对电连接器产生微振磨损[8]。振动的幅度与频率的不同，对电连接器性能的影响也不尽相同[9]。振动应力导致的电连接器接触表面机械变形和损伤会影响电连接器的额定电压、电流等电性能，绝缘电阻、耐压等安全性能以及插拔力、机械寿命等机械性能[10]。振动会引起电连接器接触表面产生微动磨损，导致接触配合不良，造成电流瞬断，而且振动产生的摩擦热会进一步促进氧化膜层的生长，致使电连接器的接触性能发生变化[11]，而振动的幅度与频率的不同，对电连接器性能的影响也不尽相同[12-13]。

电连接器的接触件是以锡青铜为基体材料[13]，其表面有镀金层。基于镀金工艺问题，在镀金层的表面存在很多微孔和裂纹，这些微孔和裂纹会直接暴露出基体材料。空气中的水分子会进入到接触斑点表面裸漏的基体材料内部，经过一定时间后会形成电解液。由于铜和金的电极电位不同且铜的电位低于金，在金-铜界面会形成原电池，进而形成氧化腐蚀物Cu2O ，如图1 所示。当反应物所处的环境温度越高时，参加反应的分子内能就会越大，反应速率也会随之加快。累积的氧化腐蚀物不断地堆积在斑点表面，从而加速了产品的失效进程，使得接触电阻不断增大，最终可能出现接触失效[14]。

图1 裸漏基体材料的氧化腐蚀Fig.1 Oxidation corrosion of bare leaky matrix material

插拔对电连接器接触件造成的直接影响有2个方面：接触斑点剪切断裂与材料转移、接触斑点磨损。接触斑点在长期的贮存过程中，斑点表面的镀金层和氧化膜层在插孔提供的接触压力作用下会紧密接触，并会出现原子之间的相互扩散运动，使得插针和插孔构成的接触斑点之间产生轻微的粘着现象。当对电连接器进行拔出、插入2个相反方向的运动时，接触斑点表面材料会在插拔应力作用下被剪切撕裂，剪切断裂的材料颗粒大部分停留在接触斑点表面，其余部分会与下一斑点发生粘结，这会使得接触斑点的形态和位置发生一定的变化，从而导致接触性能出现一定的退化。另一方面，剪切撕裂会产生新的微孔，使基体铜出现裸漏，裸漏的基体铜在温度应力作用下缓慢氧化生成新的氧化腐蚀物，使膜层电阻增大[15]。在插拔应力作用下，接触件表面的接触斑点间会发生刮擦磨损现象。插拔剪切的材料颗粒停留在接触界面上并会刮擦斑点表面上的镀金层，使得基体铜出现裸漏。此外，插拔也会引起接触斑点表面的微孔扩散和裂纹扩展，由此带来的影响是基体铜的进一步裸漏[16-18]。

2 插拔分析

实际生产中，连接器插孔在根据图纸制造出来之后，插孔直径略大于插针直径，插孔与插针之间属于间隙配合。因此，插孔在制造成型后需要对插孔簧片进行收口处理。

接触件为圆柱式开槽结构，依靠插孔簧片的弹性变形产生接触压力，插孔结构可简化为悬臂梁模型。接触压力表达式为：

式（1）中：E为插孔材料的弹性模量；δ为挠度；L为簧片长度；Ix为中性轴x的截面惯性矩。

由于不考虑惯性力和阻尼影响，采用静力学分析模块可以提高计算速度，节省计算资源，而且能够满足插拔分析的仿真需要。

2.1 模型建立及前处理

根据中航光电科技股份有限公司提供的图纸数据，使用Solidworks来建立GJB 599A型电连接器插针插孔的三维模型，并对模型进行合理处理和简化，单个接触件模型如图2所示。

图2 接触模型Fig.2 Contact model

插针半径为1 mm，插孔半径为1.05 mm，插孔为双开槽结构，插针与插孔间为间隙配合。GJB 599A型电连接器的接触件基体材料为QSn4-3，接触件材料参数见表1。由于镀层较薄，只是对表面摩擦有影响，并不能对接触件的机械性能产生影响，因而建模时使用镀层的摩擦系数，结构上建模忽略镀层。

表1 接触件基体材料力学属性Tab.1 Mechanics properties of contact basis material

网格为四面体网格，划分方式为自适应方式，为防止网格产生明显畸变，在插孔簧片外圆弧面和插针头部倒角半圆面这些接触区域的相邻面进行网格细化，细化程度系数为1，模型的网格划分情况见图3。

图3 模型网格划分图Fig.3 Graph of model grids

2.2 设置载荷及求解

接触件插拔动作的仿真过程总共分3步：第1步，为插孔簧片施加收口力10 N，使插孔簧片产生要求的屈服变形，将变形结果用Workbench 的Beta 功能更新到模型中，得到具有实际收口量（0.16 mm）的插孔模型，如图3所示；第2步，插针匀速插入插孔，至插孔内2.5 mm 处停止；第3步为插针匀速拔出插孔的过程，至起始位置处停止。

图4 插孔收口模型Fig.4 Model of shell nosing

2.3 仿真结果及分析

第一载荷步仿真的是插针插入插孔的过程。载荷步时间为0～2 s，插针从0 s 开始向x轴负方向匀速直线运动。在0.68 s 时，插针开始与插孔簧片接触，插针头部圆形倒角和插孔簧片唇口倒角开始出现应力，插针插入受阻，插入力从0开始快速上升；随着插入量的增加，插入力逐渐增大，在0.8 s 时，插针与插孔的位置处于开始接触与插针圆形倒角完全进入簧片收口端倒角的中间阶段，插入力达到峰值，为2.8 N，插拔力如图5 所示；在0.88 s 时，接触压力最大，为120.89 MPa，接触压力如图6所示；在0.96 s 时，插针圆形倒角完全插入插孔簧片倒角，簧片变形量达到最大，为0.08 mm。此时，插针插入插孔0.42 mm，插入力为1.87 N。当插针与插孔稳定配合后，插孔簧片变形量不再增加，簧片变形量如图7所示。

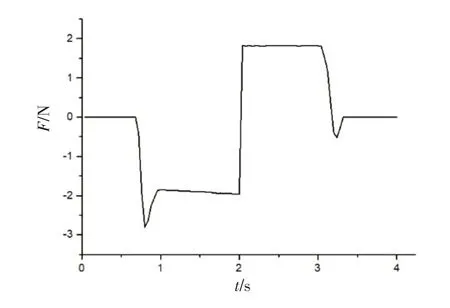
图5 插拔力Fig.5 Insertion and extraction force

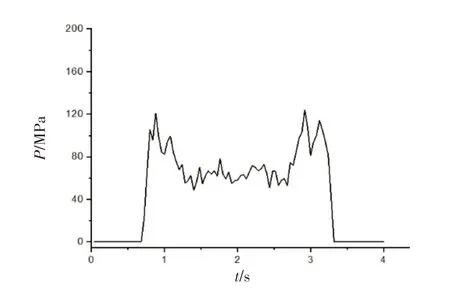
图6 接触压力Fig.6 Contact pressure

图7 簧片变形Fig.7 Reed deformation

第二载荷步仿真插针拔出插孔的过程。载荷步时间为2～4 s，插针从2 s 开始向x轴正方向匀速直线运动。第2 s 开始拔出，拔出力保持为1.8 N；从第3 s开始，插针与插孔簧片逐渐分离，接触区域变小，摩擦力变小，拔出力开始减小；从3.2 s 开始，拔出力出现负值，这是因为拔出过程中，为保证插针匀速运动，需要为插针提供一定推力来抵消簧片收口端对插针的弹力；到第3.32 s 时，插针与插孔完全分离，插拔力为0。

在插针插入的过程中，最大应力位于簧片根部截面内侧开槽处。插针完全插入后，应力数值趋于稳定，应力主要分布在簧片根部，最大值529 MPa，应力梯度显著，如图8 所示。簧片应力主要集中在截面内侧和外侧边缘，中间大部分区域没有应力作用，这是因为在插针插入的过程中，插孔簧片的内侧受到拉伸作用，外侧受到挤压作用，插孔内侧应力如图9所示。

图8 簧片根部等效应力分布云图Fig.8 Stress distribution of strip root

图9 插孔内侧等效应力分布云图Fig.9 Stress distribution inside of jack

3 接触电阻分析

Cooper、Mikic 和Yovanovich 提出了关于微凸体接触导热的单通道模型，即单点接触模型，也称CMY模型。根据接触面温度分布，得出温度场函数和边界条件，求解热传导的微分方程，得到单点接触热阻的解析解：

式（2）中：pa为接触应力；H为接触面微硬度；Ar为实际接触面积；Aa为名义接触面积。

式（2）考虑了接触应力和材料微硬度，便于对接触电阻进行计算。COMSOL软件将CMY模型应用到电接触分析中，经过对相应变量的替换和简化，得到了接触电阻的表达式：

式（3）中：V1、V2为接触面两端电压；hc为接触阻抗；J1、J2为流过接触面两侧导体的电流密度矢量；σ1、σ2分别为接触面两侧应力值；n为接触面单位向量；nd为接触面的单位法向量；σcontact为接触应力值；σasp为粗糙表面平均高度；masp为粗糙表面平均斜率；p为单点接触应力；Hc为表面微硬度。

3.1 模型建立及前处理

将之前通过ANSYS建立的连接器接触件插合状态模型导入COMSOL 仿真软件，生成有限元分析模型，实体如图10所示。

图10 COMSOL实体图Fig.10 Stereogram in COMSOL

对电连接器接触电阻的仿真涉及电阻热、固体力学的建模。因此，须要选择焦耳热多物理场，对应电流、固体传热、固体力学物理场接口，需要考虑的多物理场为电磁热，对模型进行稳态分析。定义插针、插孔基体材料为锡青铜，材料属性如表2所示。

表2 接触件基体材料热、电属性Tab.2 Thermal and electrical properties of contact basis material

3.2 设置载荷及求解

电流物理场中，接触件材料为固态金属，因而材料类型选择为固体。通常针孔结构的电连接器电流流向为从插针流向插孔，所以设置插孔尾端接线端面为接地面，在插针尾端接线端面施加1 A 的终端电流。电子接触对选择插针插孔接触对，收缩电导选择CMY相关性，电导率选择基于温度的线性电阻率。

在固体力学物理场中，材料设置为各向同性，杨氏模量、泊松比和密度等材料特性全部来自表1 给定值。力学的接触对同样选择插针插孔接触对，接触压力算法采用增强拉格朗日算法。根据ANSYS中仿真的接触压力，在接触压力初始值中输入相应值，模型初始温度设为24.3℃。

3.3 仿真结果及分析

1）接触电阻随接触压力的变化。通过ANSYS仿真得到连接器接触件在不同接触压力下接触的接触模型，导入COMSOL 中，分别进行接触电阻的仿真计算，得到接触电阻与接触压力的关系如图11所示。

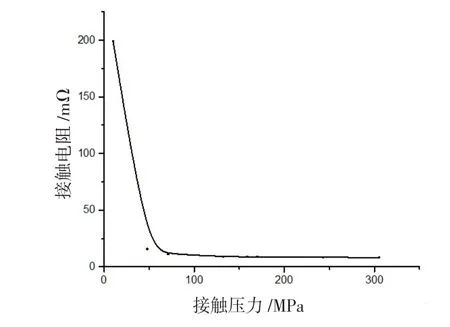
图11 接触电阻与接触压力关系图Fig.11 Diagram of relationship between contact resistance and contact pressure

接触压力越大，宏观层面接触件之间总的接触面积就越大，微观层面每个接触区域内接触的导电斑点变形越大，导电斑点的接触区域就越多，收缩电阻减小。同时，接触压力还会破坏膜层电阻，接触压力越大，表面膜层破坏越严重，膜层越薄，膜层电阻越小。

2）接触电阻随接触面状态的变化。由理论分析可知，接触电阻的大小与接触表面状态具有直接联系，通过COMSOL 分别仿真接触表面粗糙平均高度和粗糙斜率与接触电阻的关系，如图12、13所示。

由图12、13可知，粗糙平均高度越高，粗糙斜率越小时，接触电阻越大。这是因为粗糙平均高度越高，微观上各凸起接触的面积就越少，电流就会在更小的接触面形成更大的收缩电阻。当粗糙斜率减小时，接触面上的凸起就会呈现“短粗”的特征，导致实际接触面积减小。当粗糙斜率增大时，接触面凸起会呈现“陡峭”的特征，产生一些啮合点，也容易塑形变形产生更大的接触面积。

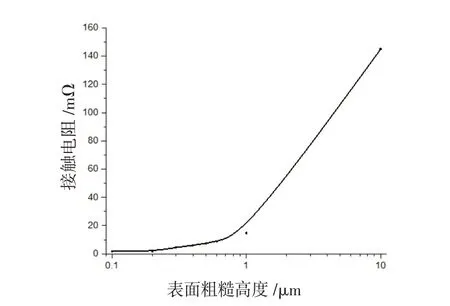
图12 粗糙平均高度与接触电阻关系图Fig.12 Diagram of relationship between contact resistance and average height of rough

图13 粗糙斜率与接触电阻关系图Fig.13 Diagram of relationship between contact resistance and rough slope

4 振动分析

4.1 模态分析

模态分析对于研究结构动力学具有重要地位，它根据模型的结构属性和材料属性，通过矩阵形式来反映单元质量和刚度，将多自由度系统简化为单自由度系统求解特征值问题，从而获得模型的固有频率、振型和对于载荷的动态响应等模态参数。

将插合状态下的模型进行模态分析，固定约束保持不变。对接触件进行模态分析，前6 阶固有频率见表3。固有模态如图14所示。

表3 连接器固有频率Tab.3 Inherent frequency of connector

图14 接触件固有模态云图Fig.14 Natural vibration mode of connector

4.2 瞬态动力学分析

瞬态动力学分析反映载荷随时间变化时的结构响应，可以对振动过程中结构响应进行仿真分析。瞬态动力学分析采用非线性的瞬态动力学方程，允许使用非线性的材料、几何和接触类型，考虑惯性力和阻尼力，瞬态动力学模块适合对插针插孔的摩擦接触模型仿真。对模型分别在x方向和y方向施加激励载荷，载荷的动力学方程为：

式（4）中：A为振幅；f为振动频率；θ为相位角。

最小步长时间Δt是瞬态动力学分析的关键参数，最小时间步长应该小到足够获取响应频率、载荷突变和接触频率等动力学现象。为保证求解精度和计算结果的准确性，每个振动周期设为一个计算步，每个计算步内设立20个子步，使得最小步长时间Δt满足：

瞬态动力学分析使用插孔收口的配合模型，前处理与插拔分析基本一致。

由动力学模型可知，插针的振动状态与外部环境基本一致，插孔簧片处于受迫振动状态。仿真时，分别在插针插孔平行轴线的水平方向和垂直轴线的垂直方向施加振动载荷，仿真振动方案如表4所示。

表4 步进振幅激励表Tab.4 Amplitude of load

先根据式（4），计算出对应时间点的位移载荷，再由式（5）确定最小时间步长，完成相应仿真参数的设置，进行求解。求解结果中，选取每个振幅的振动周期中最小接触压力，绘成曲线如图15所示。

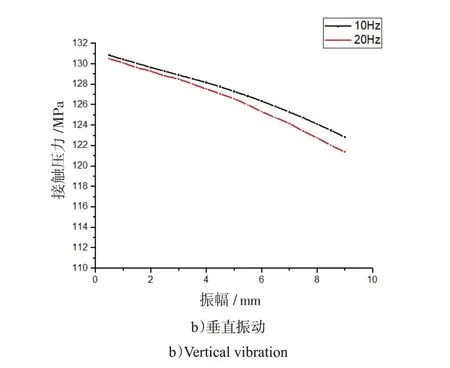
图15 最小接触压力与振幅关系图Fig.15 Relevance between minimum contact pressure and amplitude

图15表示了在一定频率振动时，最小接触压力与振幅的关系。由图可知，当振动方向和振动频率保持不变时，最小接触压力随振幅的增大而减小。水平振动时，振幅越大，最小接触压力下降的速度越快。同一振幅时，10 Hz 振动时的接触压力大于20 Hz 时的接触压力。这是由于在频率保持不变时，振幅越大，接触件运动的速度就越快，对簧片的弹开作用也就越明显，摩擦系数越小时，这一现象越不明显。垂直振动时，最小接触压力随振幅的变化并不明显，这主要是由运动方式决定的。垂直振动时，插针、插孔间会产生明显的不同心度，虽然最小接触压力有所减小，但是平均接触压力呈显著增大趋势，不同心度的变化导致了接触区域的位置和接触面积的明显变化，接触电阻受接触压力和接触面积共同影响。

5 总结

本文介绍了电连接器的力学性能和电学性能含义，并从物理、化学微观分子层面分析了电连接器接触失效的微观机制。采用有限元仿真分析的方法，研究了电连接器的力学性能和电学性能。通过ANSYS Workbench 的静力学模块，分析插拔应力作用下的应力应变情况。在插针插入的过程中，最大应力位于簧片根部截面内侧开槽处。通过COMSOL 对接触界面的粗糙度对接触电阻的影响进行了分析，接触件粗糙平均高度越高，粗糙斜率越小时，接触电阻越大；通过ANSYS 和COMSOL 结合的方法，获得接触压力与接触电阻的关系曲线，当振动方向和振动频率保持不变时，最小接触压力随振幅的增大而减小。