自动全站仪的监测精度估算及验证分析
王伟才,彭成山,杨晨辉,张晨浩
(上海地矿工程勘察有限公司,上海200072)
1 引言
相对于静力水准、电子水平尺等仪器,自动全站仪可以获得监测点的水平和垂直2 个方面的数据。相应的,由于在隧道内影响测角和测距精度的因素较多,其对自动全站仪监测数据常要进行相应的处理。因此,需要对自动全站仪的测站精度进行估算与验证。在隧道内,其气压、温度、湿度与地面略有不同,在测试过程中选用了徕卡0.5s 级全站仪TM50,测距精度为0.6mm+1×10-6mm。通过对距离、高差的重复观测,了解其测量精度的分布情况[1]。
2 精度估算
2.1 平面精度估算
试以其测角方差为0.5″,测距方差为0.8mm[2,3]。若假定距离为200m,角度为170°18′35″,那么测得其平面坐标的公式为x=x0+scosα,y=y0+ssinα(其中,x0、y0为测站坐标;s为平距;α 为测站至目标点方位角)。由于X和Y公式类似,故以下推导仅以X为例,Y方向的精度可类似推导。由于平面坐标与距离和角度是非线性关系,应用协方差传播律求两点间高差的方差σx2,因为观测边长和观测角是相互独立的,故其方差阵为:
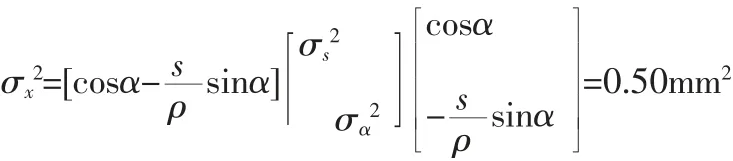
从而可得其测坐标的中误差为0.7mm,即200m 范围内,该全站仪的估算精度在0.7mm 以内。
2.2 高差精度估算
采用强制对中观测支架独立测站测量的单点高差精度的推算。若测得的水平距离为D=200m,其方差为md=0.8mm2,垂直角a=15°,其方差为0.5″,设边长观测值和角度观测值是独立观测值,应用协方差传播律求两点间高差的方差,因为观测边长和观测角是相互独立的,故其方差阵为[4]:

式中,σD为平距方差;σα为角度方差,ρ 为弧度换算秒常数,取206 265。
从而可得其中误差为0.76mm,即200m 范围内,在不考虑大气折光差的影响,精度是优于0.8mm。
3 实际验证
3.1 隧道内的大气折光差
3.1.1 隧道内的大气参数改正
以苏州轨道交通1 号线为例,通过2019 年9 月(共4 次进入隧道内)对隧道内的气压、温度、湿度的连续观测,并与地面进行对比,如表1 所示。

表1 隧道内大气参数统计表
TM50 全站仪,采用EDM 电子距离测量。EDM 本身是一种可见红色激光测距,属于1 类激光产品,其波长为785nm,最高平均辐射功率3mW,脉冲时间17ms,脉冲重复频率小于29Hz。由TM50 可见红色激光测距的改正公式[5,6]:

式中,ΔD1为大气改正值,10-6m;P为气压,mbar(1mbar=100Pa);T为温度,℃;h为相对湿度,%,α=1/273.15,x=7.5T/(237.3+T)+0.7857。将温度为24.8℃,湿度为73.6%,气压为1.02×105Pa,代入式(1)中进行计算得到ΔD1=10.23×10-6m。
3.1.2 几何水准、三角高程同名点高差较差的测定
通过对隧道内大气参数的测定,代入TM50 可见红色激光测距的改正公式中,在200m 范围内距离改正约2mm。具体实施过程中,由TM50 重复观测获得高差之差的精度较高,但通过与同点位几何水准所得高差的比较,并不一致,如表2 所示。

表2 几何水准与三角高程较差
表2 中,距离表示全站仪测站至各点之间的距离。水准测量按二等水准施测,严格控制前后视距差,采用闭合线路,观测3 次,取平均值,并进行严密平差;全站仪三角高程测量,采用单向盘左、盘右观测3 测回;通过计算,得到两种方法较差最大2.06mm。可知:
1)在隧道内“活塞风”的作用下,设距离小于150m,垂直角小于16°,则TM50 全站仪测距精度对高差的精度影响小于0.5mm;
2)高差之差的精度影响包括垂直角和距离,测点与测站距离越小,其较差越大。因此,选择测站时,应适当调整其测站与测点之间的距离关系;
3)因采用几何水准测量时,严格控制了视距和i角等,则可认为,其较差为大气折光差,根据表1 和表2 中数据可计算球气差改正系数,又因监测所获取的成果为变形量,通过近似等距、等角的观测,球气差对变形成果的影响较小,对测站控制点成果有一定的影响。
3.2 全站仪精度实际验证
测距、高差验证。本次测试,与精度估算设置条件类似,采用1 测站盘左盘右观测,使用ATR 自动锁定方式,观测14 个测回,镜站采用大棱镜组GPH1。经整理,其数据如表3 所示。

表3 外业实际验证测试数据表
通过对观测数据的整理及对距离、高差之方差的初步计算,并进行观察得出初步评价:
1)在近170m 之内,平距的均方差非常小,最大仅0.25mm,其误差的分布较为集中,且盘左盘右均值差仅为0.17mm,准确度亦较高。
2)因在自动化监测中,常采用单向单面观测,故而本次测试也采用该方法进行测量。在近170m 之内,盘左盘右的均方差较为接近,盘左为0.48mm,盘右为0.50mm,略低于二等水准常用的电子水准仪精度往返测0.3mm/km,但优于估算精度。
3)在测得的高差数据中,盘左与盘右数据均值较差略大,为-13.72mm。该数据与实际采用人工照准方式测量较为接近。这表明,采用ATR 模式观测的三角高差其精度较高,分布较为集中;不过,准确度上,存在一定的系统误差。根据厂方建议,该值需要调校。
4)若采用半测回单向观测,从监测的重复测量的特点上看,并不影响监测成果。但是,在控制网的测设中,若缺少对向观测数据的条件下,进行半测回观测,无法消除仪器自身的系统误差,这不利于控制网的测设。
4 精度分析
4.1 分布情况
表3 中均方差的计算采用14 次重复观测的数据,而在实际测量中,一周期观测某一点,通常只观测1 次。观测的方式为单向,半测回。所以,实际作业过程中的观测数据的精度不能采用重复观测数据代替,故而需要在统一设计和整体布控的过程中进行合理的设计。在表2 中,某一点高差的观测值是等精度的,通过重复观测后,获得一组观测值,即其样本各精度指标为:
若设,该组观测值X~N(μ,σ2),则其均值X¯和σ2为该组观测值的最大似然估计量。故而,在该组观测值中其算术平均值即为点估计值。其样本标准差与二阶中心矩之差尽管很小,但样本标准差相对来说,更贴近于实际情况,如图1 所示[7]。
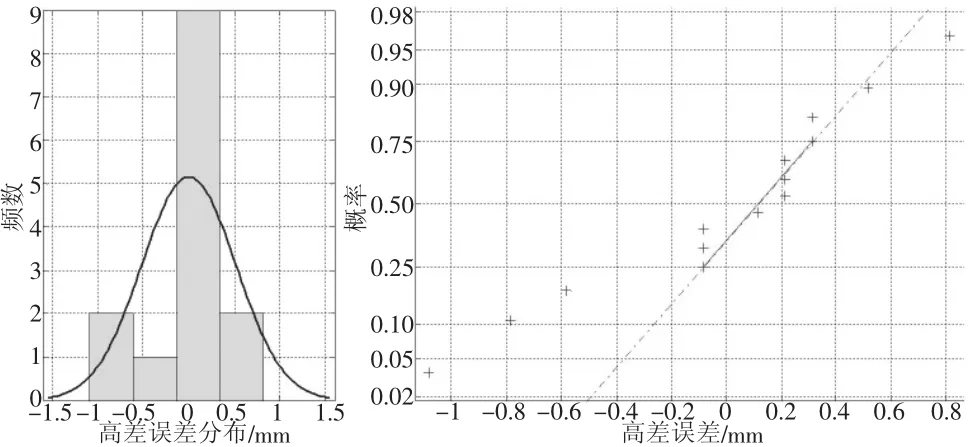
图1 误差分布及概率分布图
然而,在实际作业中,为节约时间,提高观测效率,以牺牲精度为代价,通常只进行单方向、半测回的观测。在观测的过程总是出现个别点变量较大的情况,这也反映出点估计值并不能完全代表实际作业过程中的误差分布情况。
4.2 方差σ2 的包含区间
σ2 的无偏估计为s2,则有方差σ2的包含水平为1-α 的包含区间为:
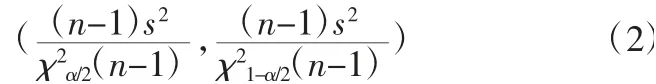
在表2 高差样本中,设标准差σ 的包含水平为0.955。则有,α/2=0.0225,n-1=13,计算得χ20.0225(13)=25.084 6,χ20.9775(13)=4.8917,S=0.51 代入式(2)中,得σ2包含水平为0.955 的包含区间为(0.13,0.69),即标准差的包含水平为0.955 的包含区间为(0.37,0.83)。
由于绝对值大于3 倍中误差的偶然误差出现的概率为0.3%,为小概率事件,通常以3 倍中误差作为偶然误差的极限值。σ 的包含水平取0.997 时,则α/2=0.001 5,计算得χ20.0015(13)=33.368 1,χ20.9985(13)=2.823 3,S=0.51 代入式(2)中,得σ2包含水平为0.997 的包含区间为(0.10,1.20),即标准差的包含水平为0.997 的包含区间为(0.32,1.09)。
由此可见,要满足P(-3σ<Δ<+3σ)=99.7%的极限误差,其绝对值的分布在区间(0.32,1.09)之内几乎为必然事件。
5 结语
实际监测过程中,每期数据观测结束后,要对本次成果与上次成果的数据进行比较,判别其产生的次变量是由误差引起的,或者是监测点的位移量。这需要建立一个基础数据库,通过该基础数据库计算方差,并进行区间估计,在区间之内则可认为是由误差引起的变量值;不在区间之间的则可认为是误差产生的低概率事件,或者可认为是变形值。
这样,在自动化监测设计时,其高差的观测不能仅观测几个测回,或者是几个单方向的半测回,而是在初值采集过程中,有必要对其150m 范围内的典型测量进行多测回的观测,并计算中误差,以作为判别累计位移量的基础数据。
本文对自动全站仪的测站水平及垂直方向的观测精度做了一定程度的探讨,并通过实际验证对隧道内的影响因素气压、湿度、温度进行了测量计算。从实际测量模式出发,对观测点可能出现的数值情况进行一定程度的计算,为了解自动全站仪测站精度提供了一个新的思路,供各同行参考。

