基于改进阈信函数的小波去噪算法研究
葛佳悦 唐春晖


摘要:为更好地消除心电信号(ECG)处理过程中存在的基线漂移、工频干扰和肌电干扰等噪声,提出一种基于改进小波阈值的去噪算法。该算法选定coi5作为小波基进行分解,选取分解尺度为8层,使用改进的阈值选取方法对每一层信号系数进行去噪。该阈值函数不仅克服了硬阈值函数不连续的缺点,而且解决了软阈值函数存在的恒定偏差,同时具有良好的自适应性。实验结果表明,该方法与传统阈值法相比,信噪比提高了24.26%,均方误差降低了21.42%;与当前国际上先进的去噪算法相比,信噪比提高了2.01%,均方误差降低了6.9%,去噪效果显著提升,验证了该算法的有效性。
关键词:心电信号;小波变换;阈值;去噪算法;信噪比
DOI:10.11907/rjdk.192684 开放科学(资源服务)标识码(OSID):
中图分类号:TP312文献标识码:A 文章编号:1672-7800(2020)006-0061-05
0 引言
心电信号(Electrocardiogram,ECG)处理是生物医学领域重要的研究对象之一,心电信号参数提取是心电图信号分析诊断的关键,其准确性和可靠性直接影响到心血管疾病的诊断与治疗效果。但心电信号较为微弱,在采集过程中,由仪器本身、人体其它信号、人体活动等因素带来的噪声对心电信号的影响不可忽略,如工频干扰、基线漂移、肌电干扰、运动伪差等,故心电信号去噪是心电信号研究的前提。
针对心电信号去噪的处理,Huang等提出的经验模态分解(Empirical Mode Decomposition,EMD)方法可实现自适应分解,但在分解过程中会产生模态混叠、端点震荡效应,影响去噪效果。为了克服这一缺点,Wu等提出以EMD方法为核心的集中经验模态分解(Empirical Mode De.composition,EEMD)算法,基于高斯白噪声频谱分布均匀的特点,通过在原始信号上多次加入白噪声的方法成功解决了模态混叠问题,但信号分解后的模态分量计算量非常大。小波变换能够提供一个随频率改变的“时间一频率”窗口,具有良好的时频特性,不仅能获取到频率,而且能够准确地定位到时间。同时,小波变换能够利用多种分辨率解析信号,在消除基线漂移、运动伪差等干扰方面效果较好,更适用于具有局部突变的非平稳信号处理,且差分阈值运算简单,计算复杂度较小,被广泛应用于心电信号去噪过程中。
小波阈值去噪算法主要思想为:将ECG信号分解为不同层次的小波,选择合适的阈值处理各层信号系数,然后重新构建信号以达到降噪效果。确定最佳小波函数、分解层数、阈值及阈值函数的方法,是心电信号小波阈值去噪算法研究的重点。
本文提出一种新的小波去噪算法,在实现去噪效果的同时,减少去噪过程对原始信号造成的影响,最大限度保证函数连续,并且具有很强的自适应能力。通过对MIT-BIH数据库中心电信号的仿真实验,得到的信噪比与最小均方误差达到了理想效果。
1 小波变换去噪原理与方法
基于小波变换的心电信号去噪方法如下:
(1)选取合适的小波基函数对心电信号进行多层小波分解(a=2j,a为尺度,j为层数),得到各层中的近似分量(低频Aj)与细节分量(高频Dj)。
(2)对每层细节系数采用改进阈值函数进行去噪。
(3)将第N层近似分量与每一层经过处理的细节分量进行重构,得到去噪后的心电信号。
小波分解可以将原始信号分解为一系列近似分量与细节分量,并使用小波变换适当尺度中的近似分量进行特征识别,而信号噪声集中表现在细节分量上,使用一定的阈值处理细节分量,经小波重构后可以得到平滑的信号。详细步骤如图1所示。
1.1 小波基选取
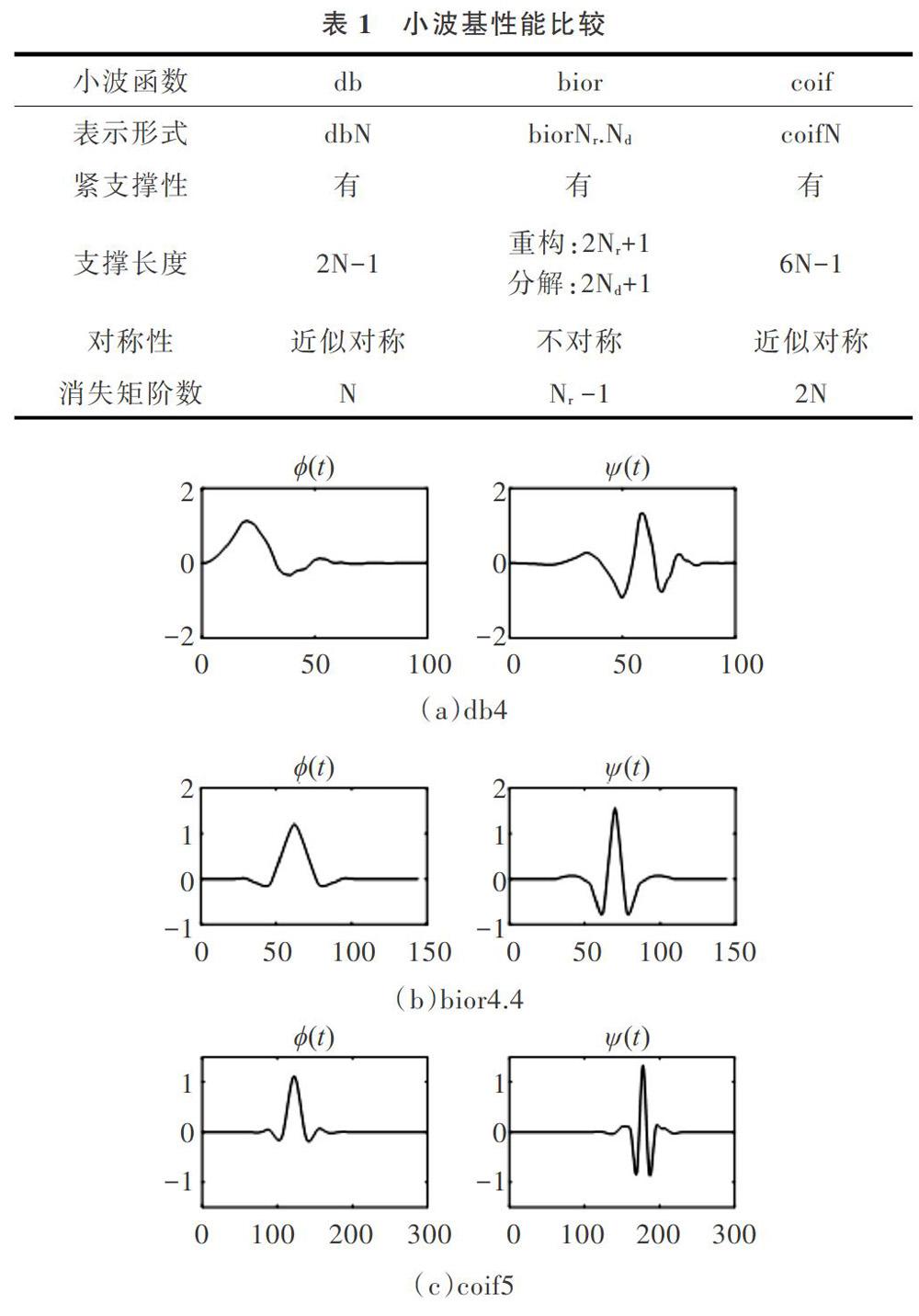
不同于傅里叶变换,小波函数不具有唯一性。对于同一个工程应用问题,采用不同小波基得到的分析结果相差甚远。适当地选择小波基,使小波函数(ψ(t))在时域上为有限支撑,在频域上也比较集中,便可使小波变换在时、频两域都具有表征信号局部特征的能力,因此有利于检测信号的瞬态或奇异点。选取小波基时主要从支撑长度、对称性、消失矩阶数和正则性4个方面进行考虑。根据心电信号特性,需重点考虑基小波的消失矩阶数与正则性。其中,消失矩越大,小波系数为零的项则越多,越有利于数据压缩与消除噪声。正则性好的小波在信号重构中可获得较好的平滑效果,并减少量化或舍人误差的影响。一般情况下,正则性越好,支撑长度越长。在当前研究中常用的小波基有db小波、bior小波、coif小波,对心电信号都可进行合理的分解重构。小波基性能比较如表1所示,尺度函数与小波函数波形比较如图2所示。
为了使有用信号分解与噪声分解对应小波系数的差异尽量明显,应选择与心电信号波形最相似的小波函数。由表1和图2可知,3种小波基中coifs函数与心电信号相似度最高,且具有良好的对称性,故本研究选取coil5小波基进行小波分解与重构。
1.2 分解尺度选取
人体心电信号频率较低,主要频率范围为0.01-100Hz,且大部分能量集中在0.1~35Hz之间。基线漂移和运动伪差在7Hz以下,其中由呼吸引起的基线漂移大约在0.5~2Hz,肌电干扰主要分布在30~300Hz,工频干扰一般在50Hz及其倍频附近。
本文选用心电数据的采样频率为360Hz,根据奈奎斯特采样定理可知,信号最高频率为180Hz。因此,第l层细节部分频率分布在90~180Hz,包含肌电噪声;第2层细节频率分布在45-90Hz,包含工频干扰噪声与一部分肌电噪声;第3、4层细节部分包含肌电干扰与心电信号的主要部分即QRS波,其能量集中在0.1-35Hz;基線漂移成分被认为主要存在于第7、8层中。第8层细节系数频率分布为0.703125-1.40625Hz,在涵盖绝大部分噪声的同时,也能保证信号的完整性,故本研究选择对小波信号进行8层分解。
1.3 阈值方法选择与改进
经过小波变换后,有用信号的能量集中在一些幅值较大的小波系数上,而噪声能量分布于整个小波域内,并且所对应的小波系数幅值较小。根据这一原理,可以利用设定阈值对信号进行去噪。
小波阈值去噪方法相比一般传统方法可实现更好的去噪效果,但仍存在一定的局限性。比如小波阈值去噪方法需根据待分析信号选择合适的小波基函数、阈值函数、阈值等,并设置可行的分解层数,缺乏一定的自适应性。在传统阈值处理算法中,硬阈值或软阈值方法都有其不足之处。其中,硬阈值是令绝对值小于阈值信号点的值为零,缺点是在某些点会产生间断,重构信号会产生一些震荡;软阈值方法是在硬阈值基础上将边界不连续点收缩到零,从而可以有效避免间断,使得重建的信号比较光滑,但由于与原始信号间有一个恒定误差,会造成信号失真、边缘模糊。
因此,需提供一种新的阈值选取函数,在实现去噪效果的同时,降低与原始信号之间的偏差,同时具有自适应性。文献中提出运用自定义阈值函数对小波分解后每一层细节系数分别进行处理,函数如下:
文献提出根据每一层小波分解的噪声水平估计调整阈值的去噪方法,且在阈值边界的小波系数采用不同表达式进行计算,适用于心电信号等微弱信号的去噪过程。该算法可根据需要调节两个参数变量α和β,不仅克服了硬阈值函数不连续的缺点,而且解决了软阈值函数存在的恒定偏差,从而在去噪的同时减少原始信号的丢失。公式如下:
其中,Wj为第j层分解得到的小波系数,Qj为第j层阈值之后的小波系数。其中,α→0,β→0为硬阈值函数;α→1,β→∞为软阈值函数。根据j的不同,阈值函数可以实现自动调节,但由于阈值λ固定,仍不能最大限度地保留心电信号有效信息。
针对阈值系数的选取,由上文可知,第l层主要为噪声,可将阈值系数直接置为0,以去除90~180Hz频率成分和基线漂移;第2-6层系数波形与心电波形较为相似,每层的频带范围递减,故阈值系数以对数形式呈现;第7-8层包含的噪声主要为基线偏移,阈值系数适当增大。具体公式如下:
2 小波变换去噪算法仿真结果
本文选用数据为MIT-BIH的心率失常数据库(MIT-BIH Arrhythmia Database)中的MLII导联数据,该数据库包含48条记录,每条记录持续时长为30min,采样频率为360Hz。使用频率为0.2Hz、幅值为0.1mV的正弦信号仿真基线漂移噪声;用频率为50Hz、幅值为0.2mV的正弦信号模拟工频干扰;采用标准差为0.02、均值为0的高斯白噪声仿真肌电干扰,将3种噪声叠加在从数据库中选取的心电信号中。
2.1 心电信号去噪结果比较
本节选取心律失常数据库中编号为100、104、105、108、201、203、222、228的8组近似无噪声的干净信号作为原始信号,采用本文第2.1节所提的db4小波、coil5小波、bior4.4小波函数及db3、db5、coif3、coil4、bior5.5、bior6.8小波基分别对信号进行分解,运用传统无偏似然估计软阈值进行处理,得到心电信号去噪效果,如图3所示。不同小波基的去噪效果可由信噪比(SNR)与其均方误差(MSE)表示。公式如下:
式中,x(n)为原始信号,y(n)为经过小波分解重构后的信号,N为采样个数。
实验结果显示,经coil5小波函数分解重构得到的去噪结果信噪比最大,表明coil5小波函数的去噪效果最好,故本文算法采用coil5小波函数作为小波分解的小波基。
2.2 改进阈值函数去噪结果比较
本节选用20组数据作为原始数据,在加入噪声后,采用coil5小波对其进行分解与重构,使用式(2)-式(4)确定每一层小波细节系数的去噪阈值,取最佳参数α为1,β为1。将本文提出的阈值函数与传统软硬阈值方法及文献、提出的阈值算法进行比较,信噪比与均方误差两项指标对比结果如图4与表2所示。
由图4、表2可知,采用本文改进后的阈值选取方法,平均信噪比为22.8055,平均均方误差为0.0027。与传统硬阈值方法相比,信噪比提高了24.26%,均方误差降低了21.42%,去噪效果显著提升;与文献中当前国际上先进的去噪算法相比,信噪比提高了2.01%,均方误差降低了6.9%,证明了该算法的有效性与适用性。采用本文算法的去噪效果如图5所示。
3 结语
本文结合传统软、硬阈值小波消噪的优点,提出一种运用自定义阈值函数的小波分解与重构去噪算法。不同尺度下的小波系数选取不同阈值,以在尽可能保留信号有效量的同时实现去噪效果。所选小波基为coif5,对信号进行8层分解,并在各层阈值选取过程中添加了阈值系数,可根据不同信号类型设定参数,具有很强的自适应性。去噪效果与现有去噪方法相比有所提高,且提高了重构信号的信噪比,减小了消噪后信号与原始信号的偏差及信号震荡。
然而,本研究尚存在以下不足:①研究中发现,在不同人体中采集的心电信号具有差异性,去噪效果也有一定差别,故如何使去噪算法更具有通用性,需要作進一步研究;②在研究过程中所选取的采样点为2000,基数较小,而在临床应用中需要处理的数据量非常大,故今后研究的重点是如何提高处理速率以适应实际临床应用需求。

