人工智能中启发式搜索研究综述
李鹏 周海 闵慧


摘要:启发式搜索(Heuristic Search,HS)是目前解决人工智能领域诸多问题的重要手段之一,在启发式搜索质量和效率评价相关定义的基础上,对目前几种典型启发式搜索算法原理进行分析,指出其优点及不足,并以人机大战为例提出启发式搜索的应用价值及未来研究方向。
关键词:人工智能;启发式搜索;评估函数;可接受启发;At算法
DOI:10.11907/rjdk.191017 开放科学(资源服务)标识码(OSID):
中图分类号:TP301文献标识码:A 文章编号:1672-7800(2020)006-0035-04
0 引言
人工智能诞生于20世纪中期,曾经历两起两落的重要历程。人工智能技术作为21世纪最前沿技术之一,其重大突破必将影响新一轮产业革命,目前它已在医学、教育、研究等领域得到了深远应用。
目前,人工智能面临的问题越来越复杂,其中以非结构化问题居多,以往盲目搜索需要搜索所有节点消耗了大量时间,这种弊病将会严重限制搜索能力,究其原因在于顾及了所有可能性,即一个一个盲目搜索。针对该问题,人们需要运用有知识的生成器避免走一些明显不可能搜索到正确答案的路径,即启发式搜索。启发式搜索已成为实际中求解智能规划问题的重要工具,特别是不确定性规划问题。近年来,放松规划在图规划问题中的探究、基于单值变量的启发式研究等均推动着对启发式搜索的探索。用启发式搜索思维构建问题解成为一种常用的思考方式,比如最大权独立集问题、普遍共享骑行问题等。启发式搜索结合模糊逻辑、频谱频率分配等领域技术更是加快了众多领域搜索发展的进程。归根究底,人们还是希望搜索路径沿着自己认为有希望的方向前进,这样就可以大大减少搜索时间。本文首先追溯研究起点,再从源头到人机大战应用对启发式搜索及其启发能力等进行探讨。
1 问题描述
启发式搜索,简而言之,即一种运用启发先验知识或者信息引导搜索方向的方法。为了评价启发式搜索的质量和效率,文中给出如下几个定义:
定义1搜索代价函数
F(p)=C(p)+H(p)
指算法在一次启发式搜索过程中,从搜索起点S(Start.point)到达目标点D(Destination)所耗费的代价(如距离等)。其中,G(p)表示从S出发到达某一中间节点p(point)的代价;H(p)表示某一中间节点p到达D的代价。
其中,当搜索已在节点p时,需要决定接下来的搜索路径,然而当前节点不知道接下来路径的真实值H(p),于是需要评估得到H*(p)。如果H*(p)的值与真实值存在较大偏差,可能引导节点向相对错误的方向搜索。于是給出如下定义:
定义2可被接受的启发搜索
在上述定义l中,对于所有可能经过的节点p,如果满足G(p)>0,H*(p)≤H(p),即中间任意一点p到S点的距离大于零,中间任意一点p到达D点的距离评估值H*(p)不大于真实值,则认为H*(p)是可以被接受的估计值,并称满足这种条件的启发搜索是可以被接受的启发搜索。
然而仅仅依据定义2的条件判定的启发式搜索并不一定最优,因为从S点出发前往某个未知p点的距离也同样需要估计。由此继续给出如下定义:
定义3搜索算法单调
在满足定义2情况下,如果对于任意节点p,满足G(p)的估计值C*(p)小于G(p),即从搜索起点S到节点p的路径是最优路径,称满足上述所有条件的搜索算法是单调的。
算法单调虽然是理想目标,但是现实问题中一般较难达到这样苛刻的条件。以下围绕搜索代价函数阐述几种不同的启发式搜索算法。
2 启发式搜索算法
2.1分支定界法
首先讨论一种特殊且简单的情况。当H*(p)=H(p)=0,即F(p)=G(p),这就是简单的分支定界法满足的条件。这种方法每次都会优先选择当前距离最短的路径前进,以最少距离为目标进行节点扩展。这种方法也会抛弃一些不可能得到最优解的节点,以此达到缩短搜索路径距离的目标。
如图1所示,(a)是待搜索的二叉树,(b)表示从起始节点A开始搜索,没有达到目的地,继续往下搜索,扩展A节点得到B和C。图1(c)发现往B方向路径距离短,并且没有达到目的地,继续扩展B节点搜索得到D和E。同理继续扩展到达图l(e),此时已经搜索到了一条到达目的地的路径,其距离为16。因为还可能存在其它路径的距离比16更小,于是继续扩展当前距离花费最小的C点(相等花费条件下遵守从右边开始扩展的规则)。直到距离可能比16小的所有路径搜索完为止,如图1(f),最终找出距离最短的路径。
简单的分支定界法固然满足定义2中启发搜索是可接受的条件,但是实际情况中H*(p)往往会有很多变化,更不可能固定为零,因此该方法显然存在较大的局限性。
2.2 两种分支定界法改进方法
2.2.1 使用低估值的分支定界法
易知上述简单纯粹的分支定界法对H(p)处理上存在缺陷,故采用对H(p)低估值的方法改进分支定界法,即H*(p)=underestimate(H(p))。显然,这种启发也是可以被接受的,同时比没有启发搜索能力的分支定界更强。
如图2所示,设矩形内的值表示该节点到目的地Goal的低估计值。从根节点开始,发现不是目标节点,则扩展该根节点,如图2(c)所示,得到两个评估函数的值20(6+14)、23(15+8),选择较小者继续扩展,直到找到了一条到达目标节点的路径,如图2(e)所示,之后继续搜索其它距离可能更短的路径,如图2(f)所示,搜索完所有可能达到最短路径的节点。
采用低估值的方法有效提高了搜索质量,更加符合实际情况,但是就其搜索速度而论并没有明显改观。
2.2.2 基于最短路径的分支定界法
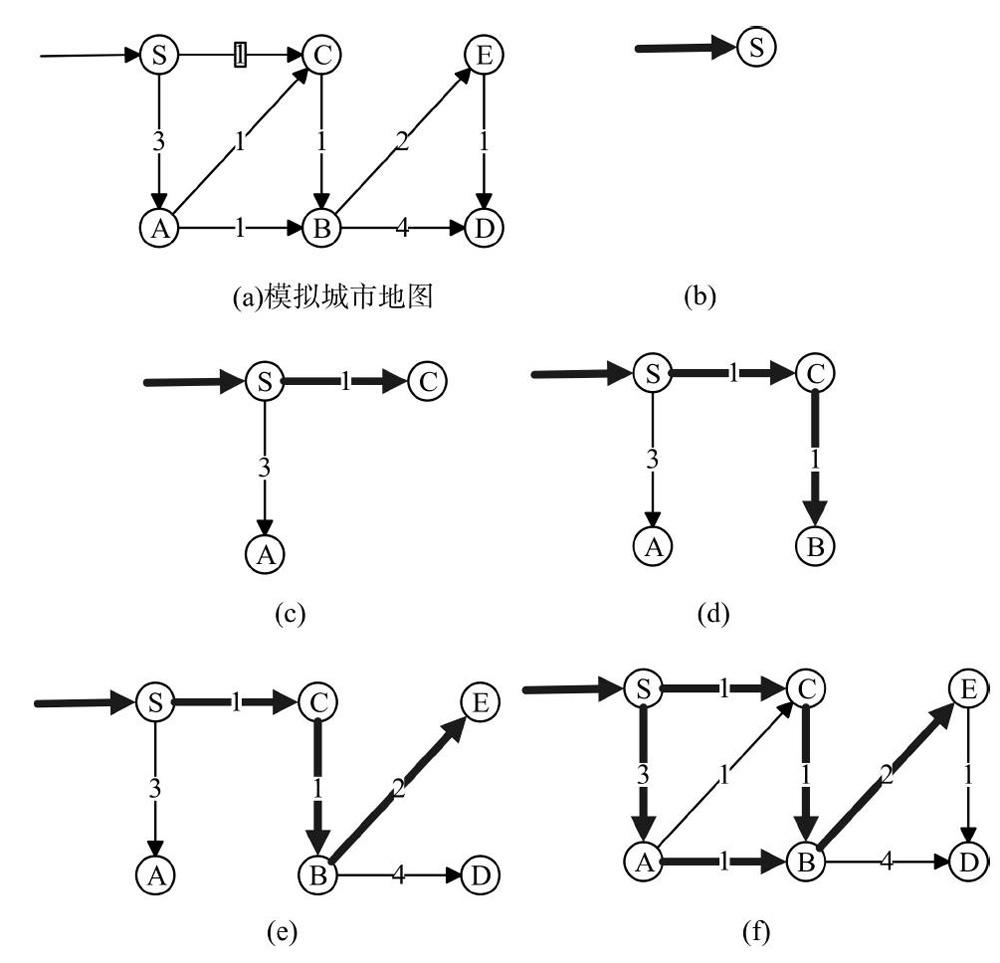
由现实生活经验可知,如果两条或多条路径到达同一节点,只需要存储距离消费最小的那条路径的距离即可。通过一个抽象处理后的实例对原理加以说明。若要求从S点城市前往D点城市,以下说明存储最短路径的分支定界法,如图3(a)-图3(f)所示。
从S点出发,面临A、C两点选择,由于C点距离更短则选择C点,如图3(c)所示。到达C点后只能前往B点,此时距离S点距离为2,如图3(d)。同理继续前往正点,如图3(e),此时距离S点距离为4。接下来扩展距离比4更小的路径,即S→A→B(其实还有另一种走法S→A→C,基于后经过优先级更高的原则选择B点),此段距离到达B时距离S点为3,此时是第二次访问B点,于是依据最短路径原则选择到达B点最短的距离2,即保证存储了最短路径S→A→B。
这类似于动态规划,要记录下已经访问的节点,下次继续访问相同节点时,只需要在已经被访问的节点中查找到达某点的最小花费取出来使用即可。虽然这种方法仅仅对到达同一节点的情况进行了优化,但也已在许多相关路径问题解决中见到它的缩影,如快递物流优选路径问题、城市路径规划问题等。
3 A*算法
上文对简单的分支定界法提出了两种优化策略,如果将两者优点结合起来就是A*算法。下面将用经典的三数码问题说明A*算法,假设采用的低估值为曼哈顿距离,其中用到的算子(简单理解,算子就是每一步的操作,具体一点也可理解为每一步的步骤)是空格上下左右4种方向的移动,具体实例如图4所示。
在图4中,标注有*号的三数码块F(p)=2+4=6的原因说明:*号三数码块距离起点完成了两个算子操作,由此G(p)=2;与Goal相比,数字l至少向下移动1步可以到达Goal,同理数字2、3分别是2步和l步,因此步数相加为4步,即H*(p)=4。另外,*号数码块与起点数码块状态相同,因此通过比较存储最短距离对路径进行优化。
由此还可以观察到,用曼哈顿距离作為搜索低估值时,有时收敛会更加快速。其实,空格的上下左右移动类似于走弯弯折折似正方胡同的小巷,因此曼哈顿路径又称为出租车路径。尽管A*算法已然是启发搜索能力较强的一种方法,但是在面对多条最小路径选择时有时也会存在因为搜索范围过大而导致搜索时间过长的缺点。
4 蒙特卡洛树搜索
人和机器在围棋中的较量比拼已是试验机器的试金石,其中核心部分便是蒙特卡洛树搜索。该搜索建立于二人零和博弈基础上,其搜索基础是最大最小搜索。最大最小搜索的中心思想是轮到我方搜索扩展时选择最有利于我方的扩展;轮到对方搜索扩展时选择最不利于我方的扩展。最大最小搜索有两大明显缺点:①搜索树宽度太广,导致该树非常“胖”;②搜索树深度太深,导致该树非常长。
蒙特卡洛树搜索便是一种解决这两个问题的有效方法。蒙特卡洛树中每个节点表示一种棋面,其搜索步骤如下:
(1)选择。从某点s向下扩展,根据启发函数选择进入s的某一子节点si。启发函数:
(2)扩展。选择启发函数最大值的点simax扩展。
(3)模拟。从simax开始模拟接下来的输出,一直到零和博弈结束为止。
(4)回溯。也称反向传播,用模拟的结果更新节点参数信息。
以上4个步骤反复迭代,一直到结束。列举一次简单的迭代过程,如图5(a)-图5(d)所示,圆内A/B表示O(s)。
通过计算启发函数选择扩展O为3/3节点如图5(a),然后通过模拟更新沿路经过的所有节点的值,即沿路反向传播的节点模拟次数加1,结果如图5(d)所示。
蒙特卡洛树搜索所用的启发知识不是固定的先验知识,而是通过搜索过程中模拟反向传播得到的带有概率的知识,具有及时性特征,非常符合围棋这一类多可能性且实时的特征,然而对于搜索树不是非常庞大的情况,比如象棋路径搜索,其效果就不如围棋好。
5 结语
启发式搜索已在众多领域得到了落实,比如路径规划、智能机器人等,但是在今后智能规划等任务中,仍然需要理论和实践的创新突破,例如更加精确的搜索代价函数、机器及时对当前现状进行动态更新的启发能力、尽量减少时间或空间消耗等。可以预见,有了更加高效且相对低成本的搜索策略,将对许多领域起到巨大推动作用。

