基于多变量LSTM网络的太阳黑子活动预测分析*

梁 波，林语琦，戴 伟，冯 松，杨云飞

(1. 昆明理工大学信息工程与自动化学院，云南 昆明 650500；2. 昆明理工大学云南省计算机技术应用重点实验室，云南 昆明 650500)

太阳黑子是日面上最常见的一种太阳活动现象，它们的数量随时间的变化呈现大约11年的周期变化。太阳黑子数的增加往往伴随着太阳爆发活动的增强。灾害性空间天气会引起地球磁场的扰动，干扰雷达和无线电通讯的正常工作，同时也间接影响地球的气候变化[1-2]。通过观测数据预报未来太阳活动周强度可以提前预知太阳活动。太阳活动周的预测主要是预测下一个太阳活动周活动指数的最大振幅、持续时间以及最大振幅出现的时间。

太阳活动的预测方法主要有3类：前体预测法、外推方法和模型预测法。在前体预测法中，无论是采用地磁度量值[3]还是极地测量值[4]预测太阳活动的最大幅度，预测结果普遍存在延迟。外推方法包括线性回归和非线性回归法[5-8]。模型预报法中的模型主要是指太阳发电机组[9-10]，是建立在大量物理基础上的物理模型，详见文[11]。

目前，第24个太阳活动周已经接近尾声，所以太阳活动周的预测都是围绕第25周展开[12-14]。随着机器学习和深度学习技术的出现，许多方法被应用于第25活动周的预测分析[15-17]。其中，文[15]采用长短期记忆网络模型预测了第25个太阳活动周期的峰值出现在2022年7月，介绍了如何在一个很长的太阳黑子序列中开发预测模型，并将预测结果与真实观测值之间的均方根误差作为模型预测效果的参考依据。

长短期记忆网络最早由文[18]提出，后发展为循环神经网络(Recurrent Neural Network, RNN)的一种。长短期记忆网络的工作单元由 “门” 保持或抑制单元状态以及单元内外的信息交流，单元之间按链式链接的特殊结构为数据间提供长期的依赖关系，这种信息持久化的特性被广泛应用到时间序列的相关工作中。长短期记忆网络的递归特性使得单元不会立即输出当前输入的响应，而是等待时间间隙的到来，时间间隙由时间步长控制。文[15]采用长短期记忆网络模型和时间步长为1的单变量预测方法预测了第25个太阳周期的黑子数。

本文提出了一种构建多变量的方法，结合长短期记忆网络预测未来10年的太阳黑子数，并对比了单变量和多变量分别在单时间步长和多时间步长的预测结果，最后得出最优策略预测未来10年的太阳黑子数，该策略由预测结果的最小均方根误差得出。结果证明多变量在多步长预测的效果更好，并且用图例上3个点的准确度证明了本文的结论，3个点分别是周期的起始点、结束点和最大振幅位置。

1 数 据

太阳黑子数据采用SILSO网站(http://www.sidc.be/silso/datafiles)发布的太阳黑子2.0版本中的13个月平滑月度数据(Source: WDC-SILSO, Royal Observatory of Belgium, Brussels)。从1749年6月到2019年3月，历时270年，包含3 237组数据，如图1，图中横坐标为每个太阳周期的起始日期，由太阳黑子的13个月平滑月度数据得出，发布在SILSO网站的太阳黑子周期记录中(http://sidc.oma.be/silso/cyclesmm)。例如第1个周期从1755年2月至1766年5月，第2个周期从1766年6月到1775年5月。下文将13个月平滑月度太阳黑子数简称为月平滑黑子数。

图1 1749年到2019年间的13个月平滑月度太阳黑子观测值Fig.1 13-month smooth monthly sunspot observations from 1749 to 2019

2 方 法

2.1 长短期记忆网络模型

长短期记忆网络在神经网络快速发展的当今，被广泛应用到深度学习领域，并成为一种应用广泛的神经网络模型，与基础神经网络相比，长短期记忆网络处理时间序列的特性不仅在层与层之间建立了权连接，在相同层之间也建立了权链接。长短期记忆网络模型是一种循环神经网络模型，循环神经网络是一类以序列为基础，在序列的演进方向进行递归并将所有节点按链式链接的递归神经网络，这种链式链接的特性揭示了序列之间的密切关系。长短期记忆网络解决了循环神经网络在处理长序列数据时梯度消失的问题，所以，长短期记忆网络适用于处理时间序列中间隔和延迟相对较长的事件，例如语音识别、机器翻译以及时间序列的预测。

长短期记忆网络中的工作单元内部如图2，单元接收当前时刻的输入信息xt、上一时刻的隐藏状态ht-1和单元状态Ct-1，并由3个门实现信息的持久化和抑制。它们分别是遗忘门、输入门和控制门。遗忘门通过sigmoid激活函数决定了对前一时刻的隐藏状态ht-1“遗忘” 多少信息。输入门包含两部分：(1)通过sigmoid函数选择保留什么值，(2)通过激活函数tanh生成候选向量值，二者的乘积作为一部分状态量与遗忘门中生成的ft和上一时刻状态量的乘积之和作为当前的单元状态Ct。最后，输出门通过tanh生成候选向量，经过sigmoid函数选择保留下来的信息，并将结果ht作为当前隐藏状态传输给下一个单元和上一层的同一时刻单元。

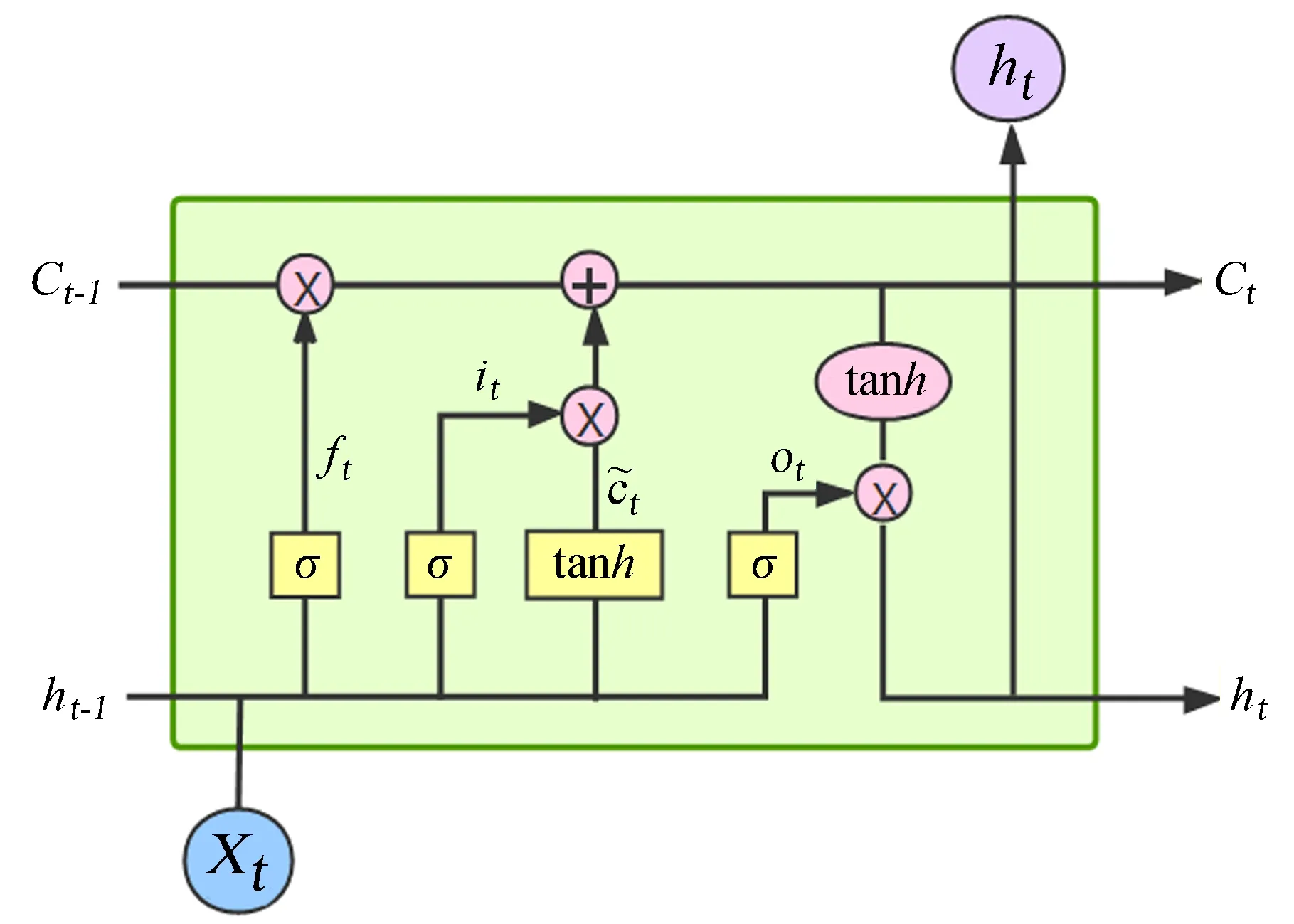
图2 长短期记忆网络单元Fig.2 LSTM cell

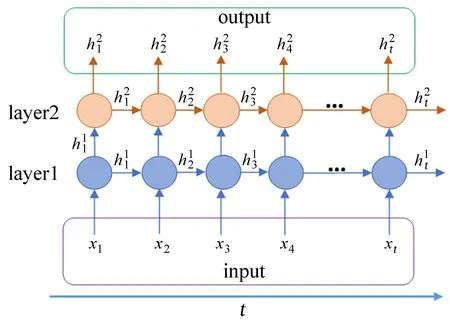
图3 长短期记忆网络的网络层Fig.3 LSTM network layers

由此可知，当设时间步长为1时，只有一个单元提供权重和输出输入的响应，所有数据通过一个单元建立时间序列数据的信息持久性。而在多个时间步长的网络中，多个单元为时间序列提供不同的权重，并且不仅在单元自身建立信息的持久性，在链式链接的单元之间也为时间序列建立信息的持久化，并增加了时间序列数据在时间上的相关性。所以，从一定程度上说，多时间步长的网络模型能为时间序列在响应过程中提供更丰富的权链接和多重的信息相关性，基于此提出了多步长的预测方法。

2.2 多步长设计

为了验证多步长方法的效果并取得最优步长，提出了多组多时间步长的策略，如表1。为了能够充分利用数据，所有的步长设置为120的约数，每组步长与滞后数之间满足跨越120个数据的间隔，这与本文的目的相吻合，即预测120个月后的月平滑黑子数。时间序列按照时间步长分为多个有序数据段，滞后数表示每个数据段起始值之间相隔的数据个数。步长为1、滞后数为120的为单步长预测，其余15组均为多步长的设计方案。

表1 时间步长策略Table 1 Time step strategy

2.3 多变量构建

在时间序列的预测范畴里，只用太阳黑子数据作为输入数据预测黑子数的方法属于单变量预测。除了上述的多步长预测太阳黑子周期，这里提出一种加入太阳黑子周期长度构建多变量预测的方法，按照第1节提到的太阳黑子周期记录，把每一个太阳黑子周期中的原黑子观测数据以它们在周期中的位置记录下来，作为除黑子原数据以外的另一个输入数据，把输入数据的维度增加到二维，这就是构建多变量的预测方法。具体方法举例：在一个黑子观测值个数为135的太阳周期中，将黑子在该周期中的观测值作为其中一个输入数据，并构建一个以0开头到134的序列，序列值与观测值一一对应。这不仅记录了观测值在周期中的相对位置，也记录了该周期的长度。月黑子平滑数在第1个最小周期开始之前有一段不完整的数据，用黑子周期的平均长132作为该不完整周期的长度，从66开始记录至132作为该67个观测值的序列。yi为太阳黑子的观测值，ki为该观测时刻的序列值，n为观测数据的个数，多变量特征表示为

[y1,k1],[y2,k2],[y3,k3],…,[yn-1,kn-1],[yn,kn].

(1)

2.4 子序列采样

在整个太阳黑子的时间序列中，为了保留观测值对时间的依赖性，采用滑动窗口的方式选择连续的子样本，从而创建多个连续子序列分别构建模型，并在已有的观测值上评价开发策略。测试采用交叉验证的方法验证模型的预测效果，使得模型有更高的可靠性。

整个数据集分为两种长度的子序列，分别称为分片11和分片6，分片11有11个子序列，分片6有6个子序列。每个子序列的数据被分为训练集和测试集，其中训练集用来训练长短期记忆网络模型，测试集用来评价长短期记忆网络预测模型。在深度学习方法中，为了使模型更健壮并且 “学习” 到更多的特征，在建模过程中使用的训练集数据量往往比测试集庞大。当数据集的样本或观测值充足时，在保障测试集的数量能够有效验证模型并且满足实验目的的同时，尽可能地扩充训练集。本文用测试集数据量的5倍和10倍分别作为分片11和分片6的训练集。此外，训练集的数据量要大于等于240，因为训练集被划分为两部分：输入序列和目标值序列，二者起始值之间相差120个数据，并且无论输入序列的长度为多少，目标值序列的最小长度为120。本文输入序列和目标值序列取相同长度，所以，当要预测未来120个月的太阳黑子数时，测试集的长度只能为120。

分片11和分片6的训练分别包含600和1 200个观测值，以及相同长度的120个测试数据，每个子序列之间起始数据分别相隔250和380个观测值，采样参数如表2。该采样方式虽然有两种长度的子序列，但两种分片跨越的数据总长度都是3 220个，序列最后的17个数据没有被采用。在最后的预测工作中，训练数据由相同采样训练集的时间最邻近数据重新构建。

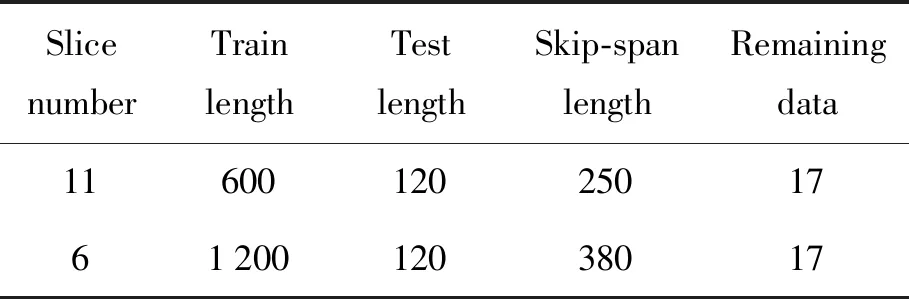
表2 分片11和分片6的采样参数Table 2 Sampling parameters of 11-slice and 6-slice

2.5 验证方法

在已有的观测值上做预测的目的是给所设计模型的预测结果提供一个可靠的依据，所以，在月平滑黑子数据集中采样后的每一个子序列采用相同的模型以及模型中相同的超参数开发预测模型，将每一个子序列预测结果与该时刻的观测值的均方根误差作为在此子序列上的预测效果。最终，对于一个完整的数据集，将所有子序列的平均均方根误差作为在该数据集上评判预测模型的效果。也就是说，对于11个子序列的采样方式，有11个均方根误差，对它们求均值，该均值就是在该种开发策略上的预测效果。

3 实验结果和分析

用PyTorch框架作为开发模型，长短期记忆网络的设计使用两个网络层，50个隐藏单元，并用Adam作为优化器，采用MAE作为损失函数。并用Visdom工具实时检测损失函数的收敛情况，模型一共训练100个周期。

结合第2.4节中的采样方式，对比单变量和多变量所有步长方案，即表1中的预测效果，分别用所有子序列均方根误差的平均值(AVG)和所有子序列均方根误差的标准差(STD)说明。

3.1 结 果

3.1.1 单变量预测

首先对比了单变量在不同步长策略的预测效果，其中包括单步长预测和15种多步长的多步预测，表3分别展示了分片11和分片6在单步长预测和最优多步长的平均均方根误差。分片11中步长为8、滞后数为15的多步长实验取得最低均方根误差平均值为43.1，相比单步长预测的45.0降低1.9，标准差从20.2降低到19.1。分片6中步长为5、滞后数为24的多步长实验取得最低均方根误差平均值为50.4，相比单步长预测的53.5降低3.1，标准差反而从16.6增大到18.1。

表3 分片11和分片6的单变量在单步长和最优多步长的结果Table 3 Univariate results of 11-slice and 6-slice in single-step and optimal multi-step

3.1.2 多变量预测

多变量的预测同样对比了在单步长和多步长方法的效果，表4分别展示了分片11和分片6在单步长预测和最优多步长的平均均方根误差。分片11在步长为6、滞后数为20时的多步长取得最小均方根误差为42.8，相比单步预测的45.4降低2.6，标准差为15.6，比单步预测的23.6减小8.0。分片6在步长为12、滞后数为10时取得最小均方根误差为51.6，比单步预测的55.1降低3.5，标准差从20.1增大到23.4。

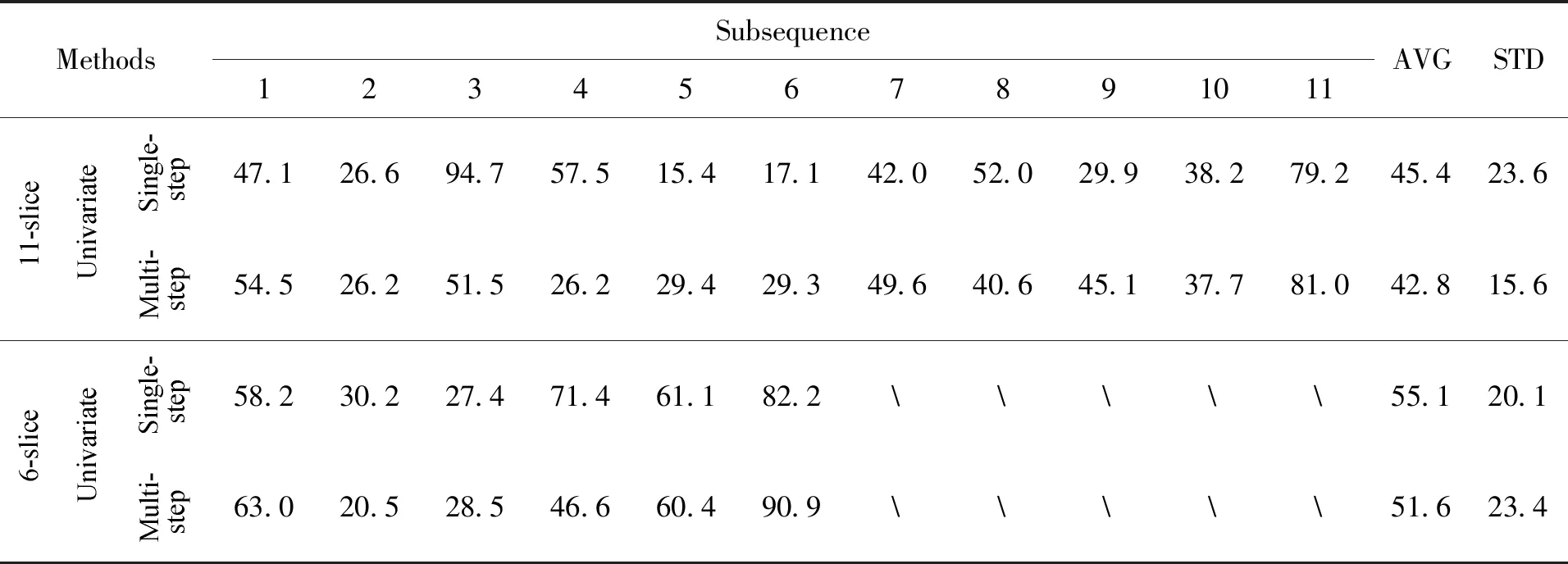
表4 分片11和分片6的多变量在单步长和最优多步长的结果Table 4 Multivariate results for 11-slice and 6-slice at a single-step and optimal multi-step results

最后分别用分片11和分片6的最优策略，即多变量的6个步长和单变量的5个步长预测了未来10年的太阳黑子数，结果见图4。在分片11中第25个太阳周期的最大振幅为144.9，出现在2022年12月；分片6的第25个太阳周期最大振幅为180.4，出现在2024年5月。

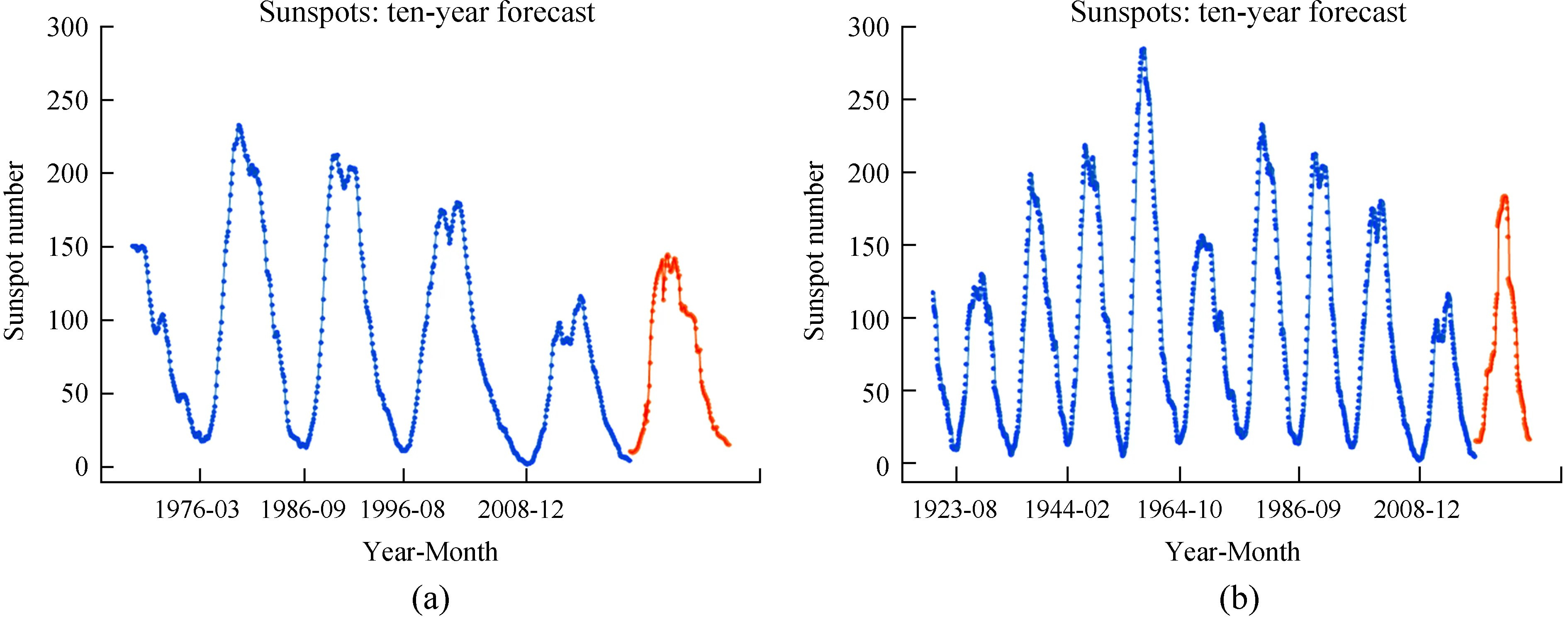
图4 (a) 分片11和 (b) 分片6预测未来10年的太阳黑子数Fig.4 (a) 11-slice and (b) 6-slice predict the number of sunspots in the next 10 years

3.2 分 析

从实验结果可以看出，就预测方法来说,无论是分片11还是分片6，多步长预测结果都比单步长的好。在单变量和多变量的比较中，分片11的多步长平均均方根误差从43.1下降到42.8，降低了0.3，标准差降低了3.5。对于分片6，虽然多步长的多变量预测反而增加了1.2，但是从结果可以看出，在第2、3和4子序列上结果都有明显的提升，但在第1和第6个子序列上误差过大使得最终的平均均方根误差大于单变量的多步长预测结果。综上所述，分片11在多变量的最优多步长，即步长为6时取得了最好的效果，不仅得到了更小的平均均方根误差，还有最小的均方根误差标准差。所以认为分片11的结果更为可靠，即未来10年的太阳黑子最大振幅为144.9，出现在2022年12月。

4 讨 论

4.1 多变量的多步长预测效果

在上述结果中，分片11比分片6效果更突出，为此以分片11为例详细对比了每个子序列在单变量单步长、最优多步长和多变量最优多步长3种方法的均方根误差，如表5。从每个子序列的均方根误差可以看出，在第2、4、5、8、11子序列中单变量的多步长预测比单步长预测误差小，多变量的多步长预测在第2、3、4、8、11子序列上误差均小于单变量的单步长和最优多步长预测结果。平均均方根误差在多变量的多步长预测中下降到42.8，相比单变量的单步长预测下降了2.2，标准差则从20.2下降到15.6，降低了4.6。

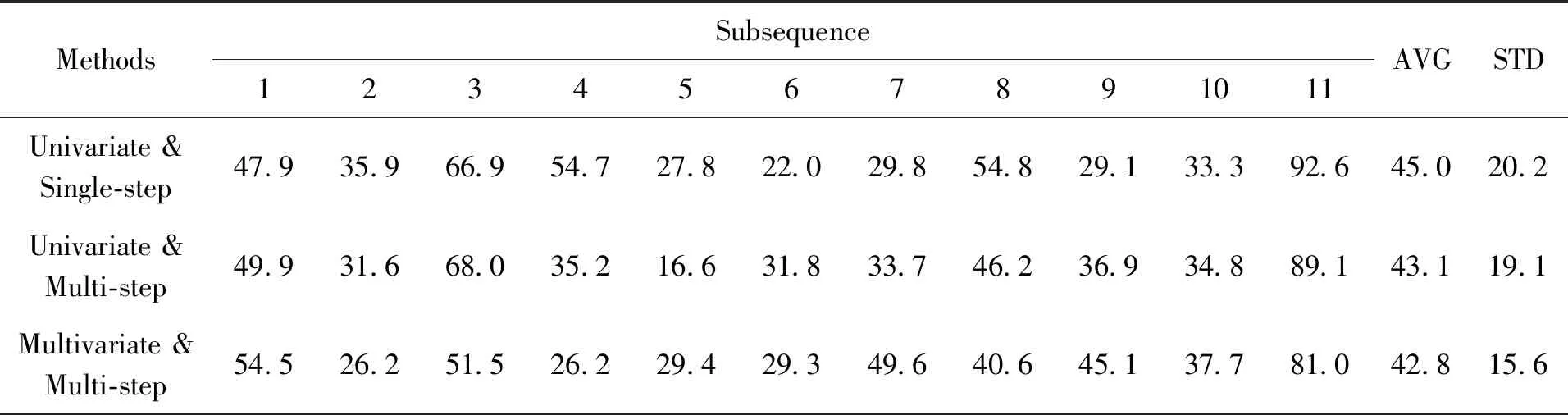
表5 分片11在单变量的单步长、最优多步长和多变量的最优多步长的结果

本文详细列举了第2、4和7个子序列在3种方法中的预测结果。如图5，每一行分别代表3个不同的子序列，每一列分别代表单变量的单步长、单变量的多步长和多变量的多步长3种预测方法。在单变量的单步长预测中，预测的黑子变化过于平滑，在极大值处很容易出现连续的水平预测值。在单变量的多步长预测中，极值处的水平变化有所改善却又波动过大。相比其他两种方法，多变量的多步长预测的极大值不仅没有处于水平变化，也没有周期内的大幅度波动，反而较为准确地预测了周期的起始和结束时间(第7个子序列)以及在该时刻的极小值，同样也较准确地预测了最大振幅的数值和出现的时间。

图5 第2、4和7个分片在单变量的单步长、单变量的多步长和多变量的多步长预测结果

第7个子序列的均方根误差在3种方法中逐渐增大，但是通过对预测结果的最大振幅、周期起始点和结束点在数值和时间上的分析，断定在最大均方根误差也就是多变量的多步长预测中有更好的预测效果，造成这种现象的原因应该是两个极值之间的预测过程中出现的波动以及相位的偏移，子序列5、6与7情况类似。第1、9、11个子序列由于所预测的周期峰值突变，造成了较大的均方根误差。

4.2 数据集与采样方法对预测结果的影响

文[15]、文[19-20]均采用了长短期记忆网络模型预测未来的太阳黑子数，其中文[15]结合SILSO的太阳黑子月度平均数据及单变量的单步长方法预测未来10年的太阳黑子数，并把数据分为6和12个子序列，训练集长度分别为1 200和840，测试集分别为600和240，平均均方根误差分别为35.9和36.9。文[20]用来自R数据集的太阳黑子月度数据及单变量的12个步长方法预测未来12个月的太阳黑子，相似地把数据分为6个子序列，训练集和测试集长度分别为1 200和600，平均均方根误差为26.9。文[19]使用与文[15]相同的数据集及单变量的单步长方法预测未来10年的太阳黑子数，将数据分为11个子序列，训练数据和测试数据分别为600和120个，得到平均均方根误差为34.4。在文[15]与文[20]训练数据和测试数据为1 200和600的结果比较中，平均均方根误差相差9.0。本文的分片11与文[19]有相同长度的训练数据和测试数据，取得的平均均方根误差为45.0，与文[19]相差10.6。

数据集本身的差异以及采样的训练、测试数据长度不一致，导致结果有较大的差异，其中采样方法不一致使均方根误差在一定程度上没有办法类比。虽然R数据集有更好的预测效果，但是因为数据只记录到2013年，导致无法采用。SILSO的太阳黑子数据与R数据集的太阳黑子数据相比更离散，黑子的波动幅度更大，导致预测结果均方根误差较差。

4.3 分片11和分片6在不同步长中的预测结果

本文对单变量和多变量在表1提出的所有时间步长策略进行了实验，如图6。结果证明，随着步长的增加，平均均方根误差呈现下降趋势，这种下降趋势在分片6中更为明显，之后随着步长的大幅度增加，误差越来越大，并且分片11的平均均方根误差总体比分片6的偏小。在所有分片的均方根误差标准差中，分片11随着步长的增多变化相对平稳，并且多变量的实验结果比单变量的总体偏小，分片6的则波动较大，尤其在单变量中。

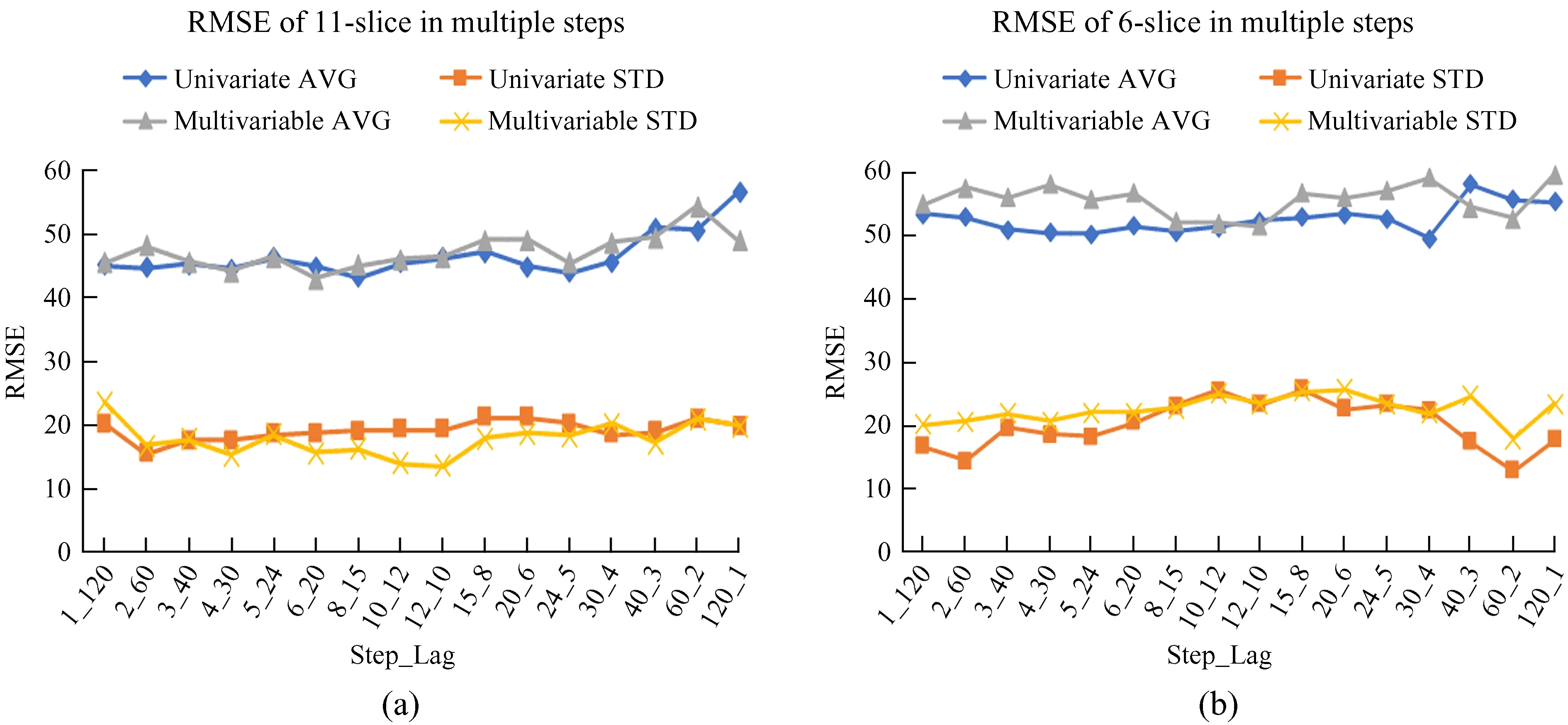
图6 (a) 分片11和 (b) 分片6在多种步长策略的预测结果Fig.6 Prediction results of (a) 11-slice and (b) 6-slice in multiple step strategies

由此可见，从总体的角度来看，分片11确实是比分片6的采样方式更好，并且在分片11中多变量的预测结果最好。

4.4 在第21、22、23和24太阳周期的预测结果

为了给预测结果提供可靠的论证，用分片11和分片6的最优策略预测了第21、22、23和24太阳周期的月平滑黑子数，图7直观地展示了预测效果，并将结果详细记录在表6中，用 “振幅” 表示最大振幅。

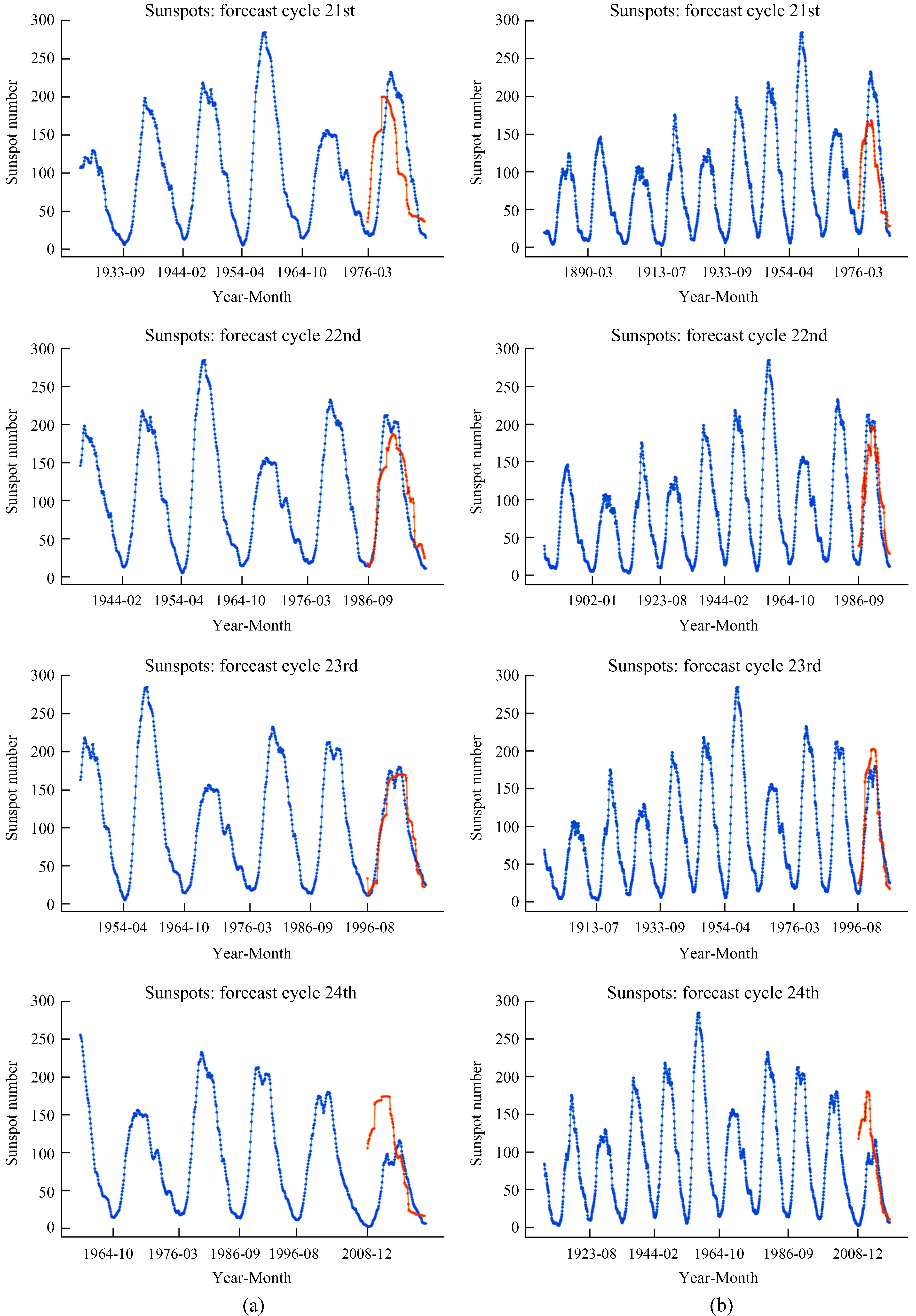
图7 (a) 分片11和 (b) 分片6在第21、22、23和24个周期的预测结果Fig.7 Prediction results of (a) 11-slice and (b) 6-slice in cycles 21, 22, 23 and 24

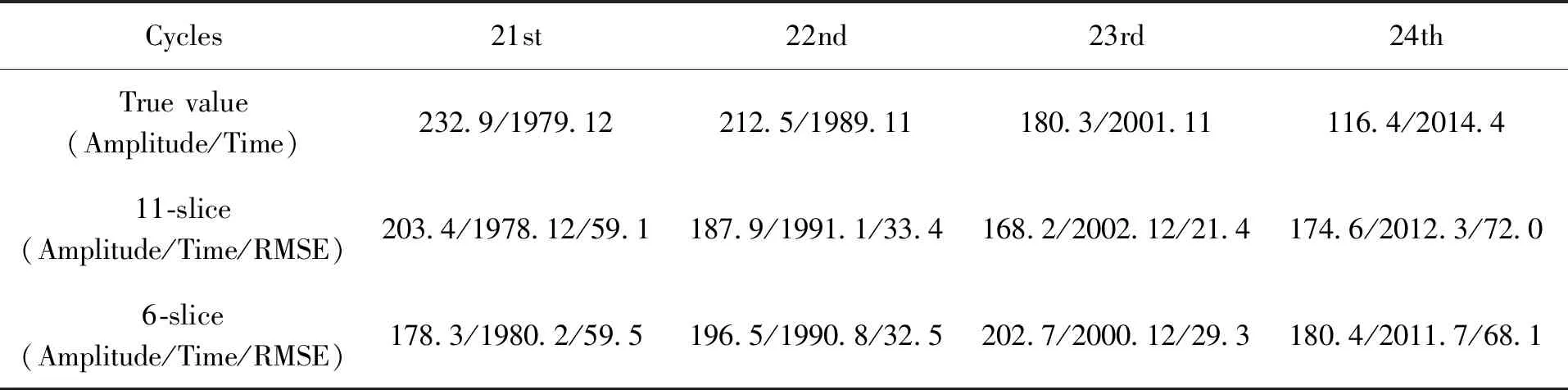
表6 分片11和分片6在第21、22、23和24太阳周期的预测结果Table 6 Prediction results of 11-slice and 6-slice in the 21st, 22nd, 23rd and 24th solar cycles

在第21、22、23和24周期的预测结果中，分片11的最大振幅与真实记录相比分别降低了12.7%、11.5%、6.7%和增大了50%，最大振幅的出现时间与真实记录相比分别提前了1年、推迟了1年2个月、推迟了1年1个月、提前了2年1个月；分片6的最大振幅与真实记录相比分别降低了23.4%、7.5%、增大了12.4%和54.9%，最大振幅的出现时间与真实记录相比分别推迟了2个月、推迟了9个月、提前了11个月和提前了2年9个月。

由以上数据分析可以看出，分片11的预测结果在最大振幅上的波动除了第22周期都比分片6小，并且4个周期的平均均方根误差为46.5，比分片6的47.4略小。而分片6在最大振幅出现的时间表现出更高的准确度，除了第24周，出现这种现象的原因：在构建模型的训练数据中分片6包含的完整周期比分片11多，所以 “学习” 到的周期长度特征更多，对此能够将时间跨度预测得更准确。在第24太阳周期预测中，振幅和周期起始时间偏差都过大，振幅偏差过大是因为与之前的周期相比，第24周期的振幅骤然下降，从而导致了偏差较大的振幅；周期起始时间偏差过大则是因为第23周期的历时相比之前的周期更久，有12年4个月，从而直接影响对下一个周期起始时间的预测。

总的来说，无论是分片11还是分片6，在各自的最优策略上取得的预测效果都不错，分片11在振幅的预测上有更大的优势，分片6在预测周期的历时上更为准确，这为本文预测未来10年的太阳黑子结果提供了有力的依据。

4.5 本文方法在太阳黑子预测上的局限

从上面的讨论可以看出，子序列的采样方式直接决定了数据特征对长短期记忆网络模型的构建，对预测结果有非常大的影响，这使子序列采样方法成为对比不同预测方法中的一项苛刻条件。在第4.4节的分析中，第24太阳周期振幅突变造成预测结果偏差较大，使得结果的准确性建立在下一周期没有发生突变的情况下。要为预测结果提供可靠的论证，只能将之前周期的 “预测” 结果作为参考，这就要求数据集的观测量不能太小，并且要合理设计子序列的长度，保证能够在训练出预测模型的同时，还能为该方法的效果提供合理的论证。

图5中的第7个分片预测的恰好是一个完整的周期，可以看出该周期有双峰结构，在图7中的第22、23和24太阳黑子周期也都有明显的双峰结构，但在预测的结果中它们多以最大振幅处水平变化或者是单峰振幅并出现多个折点的形式表现，并没有明显的双峰结构。最大振幅处的水平变化说明训练好的模型确实有保留双峰的特性，但两个峰值之间的变化不明显，致使模型在训练过程中没有 “学习” 到双峰的细微特征而出现水平变化。

5 总 结

本文使用深度学习的经典模型长短期记忆网络开发了预测月平滑黑子数的模型，并提出了一种构建多变量的方法。通过比较分片11和分片6在多变量和单变量的16组步长上的平均均方根误差，在分片11的多变量并且步长为6时取得最小的平均均方根误差为42.8。并在详细的结果分析中，通过3个点的准确度证明多变量的多步长预测有更好的效果，3个点分别是周期的起始位置、周期的结束位置和最大振幅的位置。分片11和分片6在多变量和单变量的16组步长预测结果分析中证明分片11的采样策略比分片6有更好的稳定性和更低的均方根误差。在对第21、22、23和24周期的预测中，分片11表现出对预测最大振幅的相对优势，而分片6则在最大振幅出现的时间上表现得更准确，这些结果为预测未来10年的太阳黑子数提供了可靠的依据。换言之，在分析的过程中也能发现该预测方法的局限，例如在预测第24太阳周期中振幅突变、上一周期历时突变导致预测结果偏差较大，以及模型不够完善在预测的结果中没有体现出周期的双峰特性，这或许是该领域接下来的研究重点。

最后，以分片11的多变量在步长为6处的模型预测了未来10年的太阳黑子活动，即第25个太阳活动周期，最大振幅为144.9，出现在2022年12月，比第24周期活跃，持续时间至少为10年。