超声波流量计杂质对测量精度影响机理分析

张 蒙 杜广生 程 浩 杨 悦

(山东大学能源与动力工程学院， 济南 250061)

0 引言

工业装备是现代农业的硬件支撑，随着现代工业化的发展，农业生产的各个环节和过程逐步由动力机、水利灌溉设备、耕整机、温度控制系统、自动化喷淋装置等农业装备取代。超声波流量计量程范围广、测量精度高，具有良好的温度适应性，在农业灌溉、水利运输、温度控制、液位监测、自动化配料等领域得到广泛应用[1-3]。随着农业机械化技术标准要求越来越严格，对超声波流量计的精度和稳定性要求也变得更高[4]。

为提高超声波流量计的计量精度，研究者从不同角度出发，尝试了很多技术手段。檀盼龙等[5]针对高黏度流体在输送过程中流动状态容易受到管道变化影响的问题，提出了一种利用遗忘因子的最小二乘法进行积分权重系数优化的方法，降低了超声波流量计对高黏度测量的影响。张皎丹等[6]基于Gauss-Jacobi积分方法，提出了基于实际管路流态分布的数值积分优化方法，通过单弯头理论模型和实流实验分别进行了验证。王鉴钊[7]针对浆液循环泵管道流量测量问题，根据超声波信号特性的分析以及常见频谱细化方法的选择，将Zoom-FFT作为系统频谱分析的方法。吕美高[8]采用离散项模型对主管道内含杂质污水的运动进行了仿真，研究了大雷诺数下杂质对流量系数k的影响。SHI等[9-10]采用实验和数值模拟相结合的方法，分析了不同类型的杂质对V型声道布置下超声波信号的影响。为了探究传播介质对超声波信号的影响，陈志贤[11]测量了CaCl2溶液内超声信号横向和纵向衰减，通过实验发现，超声波可促进Ca(HCO3)2溶液结晶形成水垢。

相关研究表明，当超声波流量计安装在供热管道上，根据供热采暖系统水质及防腐技术要求，建筑物热力入口的供水干管上宜设置两级过滤器[12-13]，其中，初级为滤径3 mm的过滤器，二级为滤径0.65～0.75 mm的过滤器。对于分户热计量的住宅，流量计宜设在回水管上，进入流量计前的回水管上应设过滤器，滤网规格不宜小于0.25 mm(60目)[14]。由于含杂质水流属于非均匀介质，杂质的成分、大小、分布、在水中所占体积分数都会对测量信号产生影响，因此，对流量计内含杂质水流的研究非常必要。本文采用数值模拟计算和实验研究相结合的方法，研究杂质颗粒粒径在不同流量下对超声波流量计测量精度的影响，以提升超声波流量计的精度和适用性。

1 含杂质水流的超声波传播数值模拟

1.1 数学模型

液相采用标准k-ε模型[15-19]，k方程为

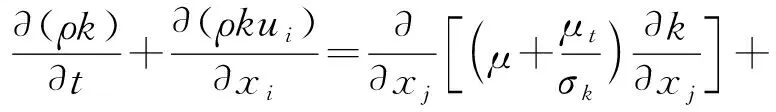
(1)

ε方程为

(2)

式中Gk——由平均速度梯度所产生的紊流动能

Gb——由浮力产生的紊流动能

YM——引起可压缩紊流中过度扩散率的脉动系数

ui——速度分量k——湍流脉动能

μ——粘性系数ρ——流体密度

μt——紊流粘性系数ε——湍流耗散率

C1ε、C2ε、C3ε——常系数

σk——系数k的紊流普朗特数

σε——系数ε的紊流普朗特数

Sk、Sε——用户自定义的源项

固相采用Eulerian模型，计算式为[19-23]

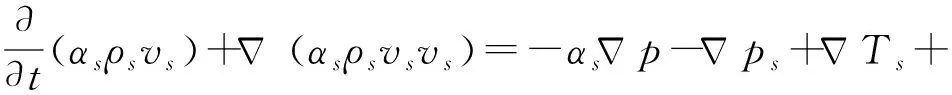
(3)

式中ps——固体压力ρs——固相密度

vs——固相速度vl——液相速度

vls——液固两相速度传递系数

αs——固相体积分数

Ts——固相间的剪切力张量

Fs——固相外部体积力

Flift,s——固相升力Fvm,s——固相质量力

Kls——液相与固相间的动量交换系数

mls——液固两相质量传递系数

固液两相的连续性方程为

(4)

式中α1——液相体积分数

v1——液相速度ρ1——液相密度

ms1——固液两相质量传递系数

1.2 物理模型

数值模拟计算的物理模型采用声道布置为U形的DN25型超声波热量表测量管段，表长度为110 mm，测量段直径为16 mm，反射柱前后长度为5 mm，换能器和反射柱直径为10 mm，间距为70 mm，结构示意图如图1所示。

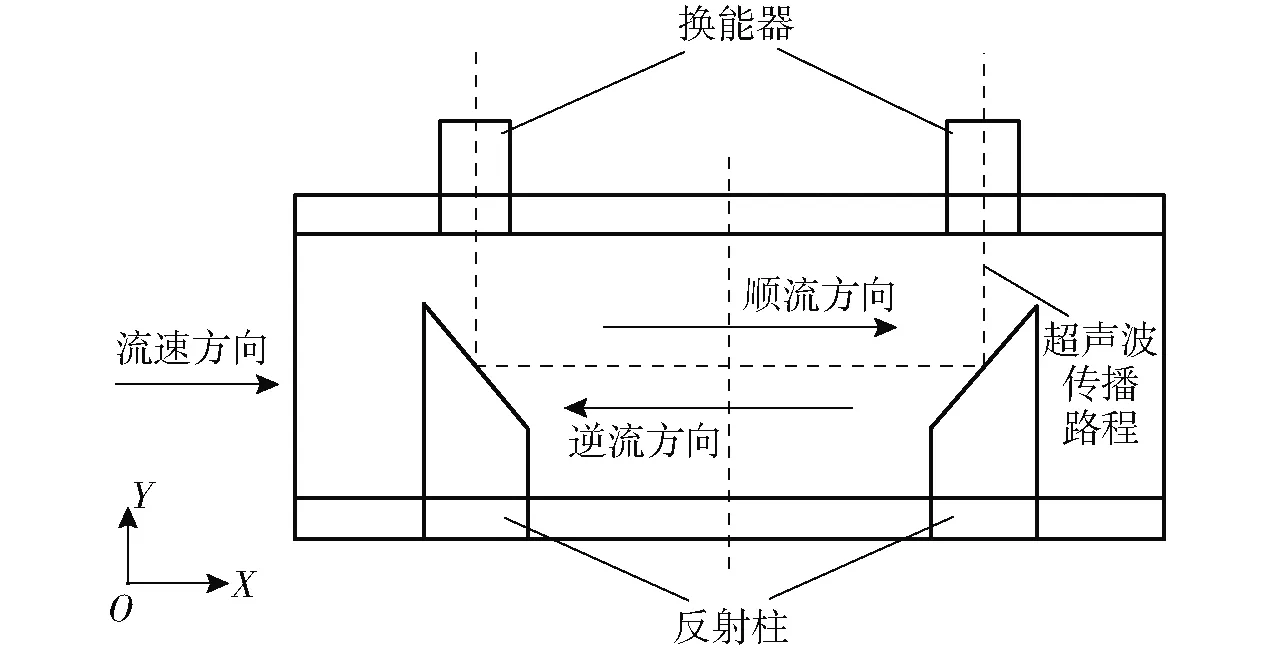
图1 DN25型超声波热量表结构示意图Fig.1 DN25 ultrasonic heat meter structure diagram

1.3 边界条件

根据水质的实际情况，选取杂质体积分数为5%的流动进行研究，杂质采用CaCO3[10-11]，密度为2.7 g/cm3。入口边界为Velocity Inlet，初始值按照充分发展状态下流体速度分布设定，考虑到实际运行状态和雷诺数变化，入口边界条件取计量标准规定的5种流量[24]：0.07、0.14、0.35、1.05、3.50 m3/h。流动区域出口设定为自由出流条件，管壁为无滑移边界。

1.4 网格划分

反射柱前后长、测量段中间位置为圆柱体结构，直接采用结构网格。测量段结构不规则处采用非结构网格。为更好地探究杂质分布规律对声波传播影响，对测量段的网格进行加密。通过试算获得网格数量满足网格无关性的要求，模型的整体网格数需超过3.7×106个。

2 杂质颗粒分布规律及其对声波传播的影响

2.1 不同流量下杂质分布规律

流道中间位置的截面作为杂质体积分数取值面，重力沿图1中Y轴负方向加载。如图2所示，坐标原点在管道中心处。考虑到超声波换能器的声波辐射宽度为10 mm，杂质体积分数取值范围为图中阴影区域。将相同Y坐标处的杂质体积分数沿X轴方向做线平均，称为该分布位置处的体积分数。

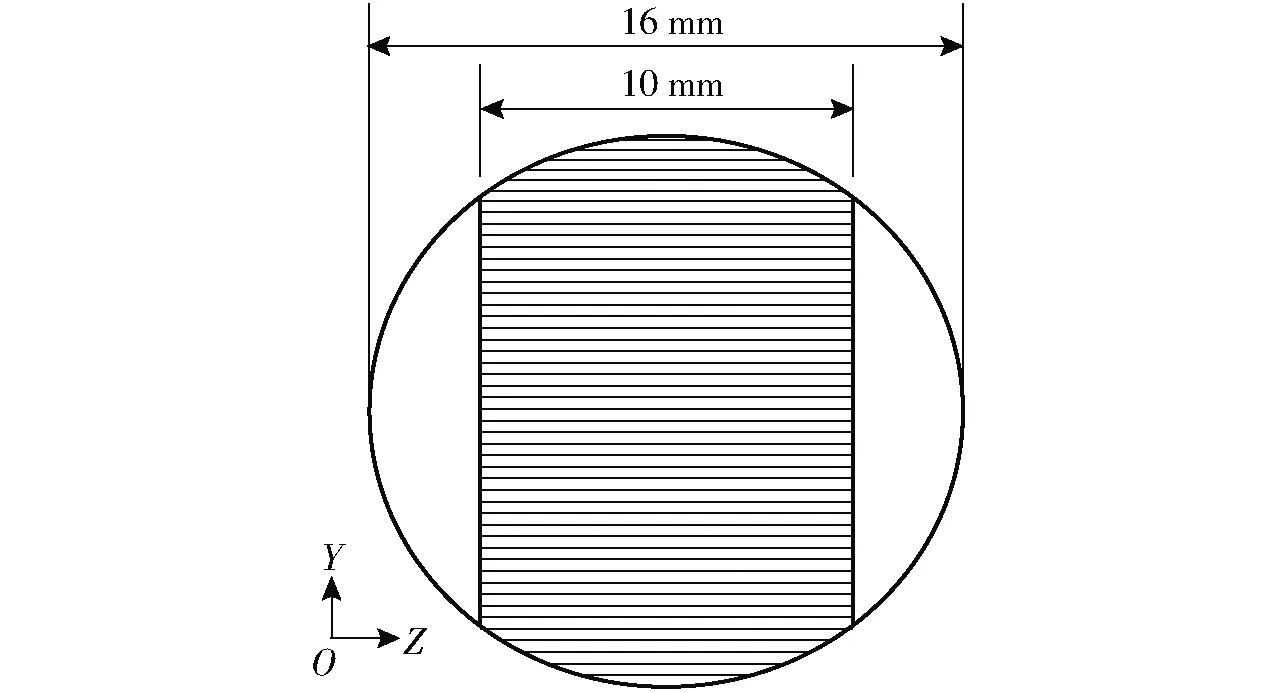
图2 杂质分布计算截面示意图Fig.2 Cross section diagram of impurity distribution observation

根据计算结果，取杂质颗粒直径分别为0.01、0.02、0.05、0.10、0.20 mm工况下不同流量点沿Y轴杂质分布情况，如图3所示。

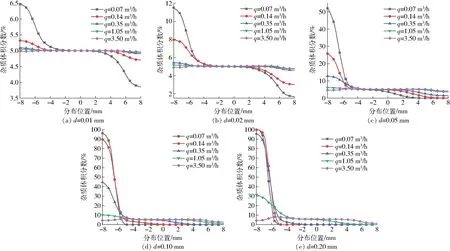
图3 杂质在中心截面的分布规律Fig.3 Distribution rules of impurity in central section

图3a为粒径0.01 mm的杂质在中心截面随流量变化的分布规律。从图3a可以看出，流量大于0.35 m3/h的工况下，体积分数基本趋于5%，在-8 mm位置处最大，产生堆积。从0.14 m3/h的流量开始，整个杂质分布可以分为3个区域：底部沉积区，体积分数最大；中部均匀区，体积分数与平均值接近；顶部沉降区，体积分数最小。

当杂质粒径增大为0.02 mm时，各流量点下的中心截面的体积分数分布曲线变化规律与粒径为0.01 mm的基本一致，如图3b所示。但底部最大体积分数增大，说明随着粒径的增大，沉积效果明显。由上述两种粒径分布曲线中心区域(-5～5 mm)的杂质分布规律可知，该区域杂质体积分数基本保持一致。即对声波传播产生的反射、散射影响也是一定的，此种情况下可以通过流量系数进行修正，确保测量精度。

随着杂质粒径的继续增大，当粒径为0.05 mm时中心截面的杂质分布规律与之前相比产生明显变化。如图3c所示，在流量3.50、1.05 m3/h工况下，杂质体积分数基本保持一致；从流量0.35 m3/h开始，随着流量的减小，底部杂质沉积逐渐增大，中间杂质保持一致的区域逐渐变小，顶部杂质体积分数逐渐变低，即在0.07～0.35 m3/h的流量区间内，杂质在中心截面的分布不稳定，对声波的影响也不恒定，对测量产生影响。即在此粒径流动下，流量1.05 m3/h以上工况，杂质在中心区域的分布一致，在流量0.35 m3/h工况下，杂质在中心区域的分布产生变化，随着流量的减小，中心区域的杂质分布变小。

当杂质粒径为0.10 mm时，杂质的分布规律与粒径为0.05 mm的基本一致，如图3d所示。在流量0.07 m3/h工况下，杂质基本沉积在-8～-5 mm的区域范围内，随着流量的增大，该区域开始变大。当流量达到1.05 m3/h，在中心区域体积分数基本一致。

当杂质粒径继续增大到0.20 mm时，杂质的沉积现象更加明显，如图3e所示。在流量0.07、0.14 m3/h时，杂质基本沉积在-8～-5 mm的区域，其他区域的杂质含量基本为零，即在这两种流量下，杂质不会对声波传播产生影响；在流量0.35 m3/h下，杂质的沉积范围增大到-2 mm，该范围已经达到声波传播的中心区域，开始对声波的传播产生影响，随着流量的继续增大，中心范围的杂质分布变大，当流量达到3.50 m3/h时，中心区域的杂质分布基本区域一致。

2.2 杂质分布对声波传播及测量的影响

通过杂质分布规律(图3)分析可知，在中心截面杂质的分布规律与颗粒粒径、流量有关。杂质粒径越小，流量越大，杂质分布越均匀；杂质粒径越大，流量越小，杂质分布越复杂。超声波信号传播路径上的杂质会影响测量精度，为研究该路径杂质的分布情况，分别对0.07、0.35、3.50 m3/h 这3种流量工况下两相流流场进行模拟，这3个流量点分别对应层流流动、雷诺数较小的湍流流动、雷诺数较大的湍流流动，流道截面内不同粒径杂质分布云图如图4～6所示。

图4 流量0.07 m3/h工况下杂质分布云图Fig.4 Concentration distribution diagrams of impurities under flow condition of 0.07 m3/h

如图4所示，在小流量工况下，随着杂质粒径的增大，杂质分布产生变化。当d=0.01 mm时，杂质区域均匀分布，中心区域体积分数一致，对声波传播和测量精度影响规律一致；当d=0.05 mm时，杂质分布不均匀，从上至下体积分数逐渐增大，中间区域处于不稳定状态，对声波传播及测量影响最大；当d=0.20 mm时，杂质基本沉积在底部区域，中间区域的杂质分布几乎为零，对声波传播及测量精度无影响。

如图5所示，流量0.35 m3/h工况下，当d=0.01 mm时，杂质区域均匀分布，中心区域的体积分数一致，对声波传播和测量精度影响规律一致；当d=0.05 mm时，杂质分布在上部分区域逐渐变大，变化区域范围进入了中心区域，对声波传播和测量精度产生影响；当d=0.20 mm时，杂质大部分沉积在底部，相比小流量工况，底部区域增大，结合图4的规律，有一部分杂质进入到中心区域，对声波传播和测量精度产生影响。

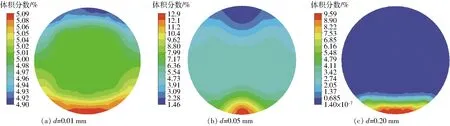
图5 流量0.35 m3/h工况下杂质分布云图Fig.5 Concentration distribution diagrams of impurities under flow condition of 0.35 m3/h

如图6所示，当流量为3.50 m3/h时，随着杂质粒径的增大，分布由原来的均匀分布逐渐向底部沉积，当d为0.01、0.05 mm时，处于均匀分布，对声波传播及测量的影响规律一致；当d=0.20 mm时，杂质较多沉积在底部，并且影响中心区域，对声波传播和测量精度产生影响。

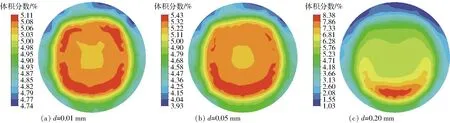
图6 流量3.50 m3/h工况下杂质分布云图Fig.6 Concentration distribution diagrams of impurities under flow condition of 3.50 m3/h

3 实验及分析

根据上述数值分析可知，信号传播路径上杂质粒径和浓度越大，对声波的传播影响也越大，势必对超声波的测量精度产生影响，因此本文通过实验研究获得杂质对超声波热量表检测精度的影响。分别在清水、加体积分数为5%的不同粒径的CaCO3颗粒两相流中进行流量测量，与标准流量计数值对比，进行误差分析。被测表为DN25 型超声波热量表，精度等级为2级。

测试实验台如图7所示。该流量检测实验台的误差精度为0.1%，符合热量表检测装置要求[25]。本文实验选用称量法进行检测。

图7 流量检测实验台Fig.7 Flow test bench

根据计量检测规程和数值模拟计算结果，实验研究测量流量分别为0.07、0.14、0.35、1.05、3.50 m3/h。

经过筛选，CaCO3颗粒密度为2.7 g/cm3，粒径为0.20、0.10、0.05、0.02、0.01 mm，体积分数为5%。在流量检测实验台的水箱中均匀混合，再对超声波热量的检测精度进行测试。

超声波热量表误差计算公式为

(5)

式中q1——被检测表的流量值

q——实验台测得的标准流量值

采用的实验方案为称量法，通过标准秤测量流过热量表的流体质量，进而计算流量q。

不同流量点超声波热量表流量测量值的相对误差随CaCO3粒径变化曲线如图8所示。

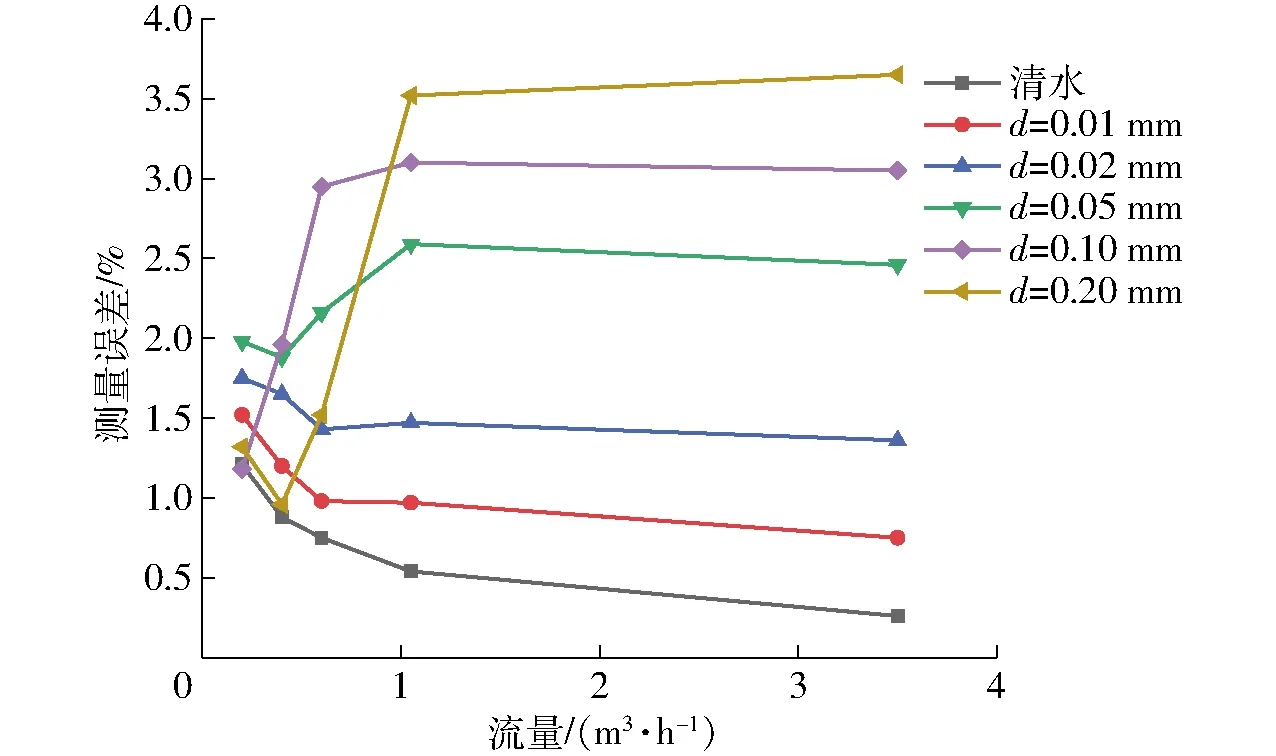
图8 误差随碳酸钙粒径变化曲线Fig.8 Error curves with calcium carbonate concentration change

如图8所示，清水工况下，超声波热量表在不同流量下的测量误差变化小于1%；随着粒径的增大，测量误差变大。当颗粒物分布相同时，粒径越大对声波的反射能力越强，声波衰减越大，如图9所示。

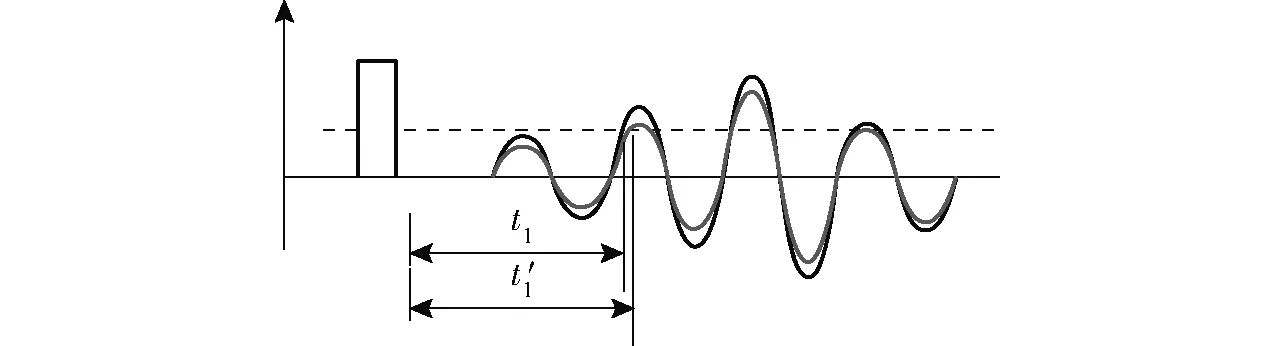
图9 接收波形放大示意图Fig.9 Waveform enlarged schematic

由于杂质存在使声波产生衰减，时间由原来的t1变为t′1，导致时差变大，产生正向误差，所以声波衰减越大，产生的误差越大。

杂质粒径为0.01、0.02 mm的情况下，测量误差相比纯水有所增大，所有流量规律基本一致。当粒径为0.05 mm时，所有流量下的误差增大，特别是当流量从0.35 m3/h开始，增大幅度变大，由图3c可知，随着流量的增大，中心区域的杂质体积分数变大，所以误差增大。当粒径为0.10 mm，流量为0.07 m3/h时，误差几乎与纯水一致，此后随着流量的增大，误差开始增大，且增大幅度逐渐变大。由图3d可以看出，流量为0.07 m3/h时，杂质基本沉积在底部，中心区域杂质体积分数基本等于零，所以对测量误差无影响，随着流量的增大，杂质在中心区域的体积分数也逐渐增大，误差变大。当粒径为0.2 mm时，流量为0.07、0.14 m3/h时，测量误差与纯水基本一致，之后随着流量的增大误差增大，对比图3e，流量为0.07、0.14 m3/h时，杂质分布没有进入中心区域，因此误差不变，0.35 m3/h杂质进入中心区域，误差开始增大，直至3.50 m3/h时，杂质分布在全部中心区域，误差最大。

流量0.35 m3/h为曲线变化分界点，在此流量点之后，不同粒径的测量误差开始逐渐趋于水平。该误差规律与上述数值模拟计算分析一致，验证了本文数值计算的正确性。

4 结论

(1)通过对杂质分布规律的分析获得中心区域分布一致的工况，即杂质粒径在0.02 mm以下，或者流量在1.05 m3/h以上时，该工况下中心区域的杂质浓度分布基本保持一致，对声波的传播和测量精度影响规律一致。

(2)通过分析获得杂质在中心区域分布几乎为零的工况，即当杂质粒径为0.1 mm、流量为0.07 m3/h，或者杂质粒径为0.2 mm、流量小于0.14 m3/h，该工况下声波传播不受杂质的影响，对测量精度无影响。

(3)通过分析获得杂质分布不稳定工况，即杂质粒径在0.05 mm以上时，随着杂质粒径的增大，杂质逐渐向底部靠拢，且随着流量的降低，中心区域的杂质分布减小。该工况下声波的传播受杂质颗粒粒径和流量的综合影响，对测量精度影响最大。