基于遗传算法的SWMM模型参数率定研究

马彦斌，盛 旺，李江云, 代文江

(武汉大学，武汉 430000)

0 引 言

美国环境保护署(EPA)开发的SWMM(Storm Water Management Model)降雨径流模型，广泛应用于对城市区域降雨径流水量、水质的动态模拟[1]。SWMM模型参数繁多，且部分参数或者具有不确定性，或者为概化结果，不具实测意义，无法直接测量，一般通过收集可直接观测数据进行模型参数率定。即通过寻找一系列适合的模型参数，使模型预测结果尽可能地接近监测数据[2]。

早期关于参数率定方法较少，以人工试错法和单参数敏感性[3]分析法为主，由于人工试错法效率低下，主观性强。随着计算机技术的发展，一系列自动寻优算法[4,5]被运用在降雨径流模型的参数识别中。采用自动寻优算法时，如果直接对模型中所有参数进行率定分析，模型计算量会随着参数维数的增加而呈指数增加，陷入“维数灾难”[6]。因此，本文将按率定参数选择和模型参数率定两个步骤进行研究。

1 研究方法

首先采用敏感性分析法确定敏感参数，模型参数的率定仅针对敏感性参数进行，借此达到降维效果，这在一定程度上降低了模型率定的复杂性，提高了模型率定的效率[7]；其次，利用收集到的研究区域实测数据，基于MATLAB中的遗传算法模块，对初步构建的城市水文模型进行参数率定。

1.1 研究区域概况

研究区域位于中山市火炬开发区张家边某居民小区。该小区于2007年建成，整体绿化率较高，区域总面积约为6.14 hm2。如图1所示，根据研究区域影像图，采用遥感软件ENVI5.1解析可得到下垫面分析结果。各下垫面类型中，路面所占比例最高，占研究区域总面积的43.97%，其次为建筑屋面以及绿地，分别占31.92%和24.11%。按照下垫面透水能力进行用地类型划分，可以把除去绿地以外的下垫面类型划分为不透水表面，则该区域的整体不透水表面所占总面积比例为75.89%。

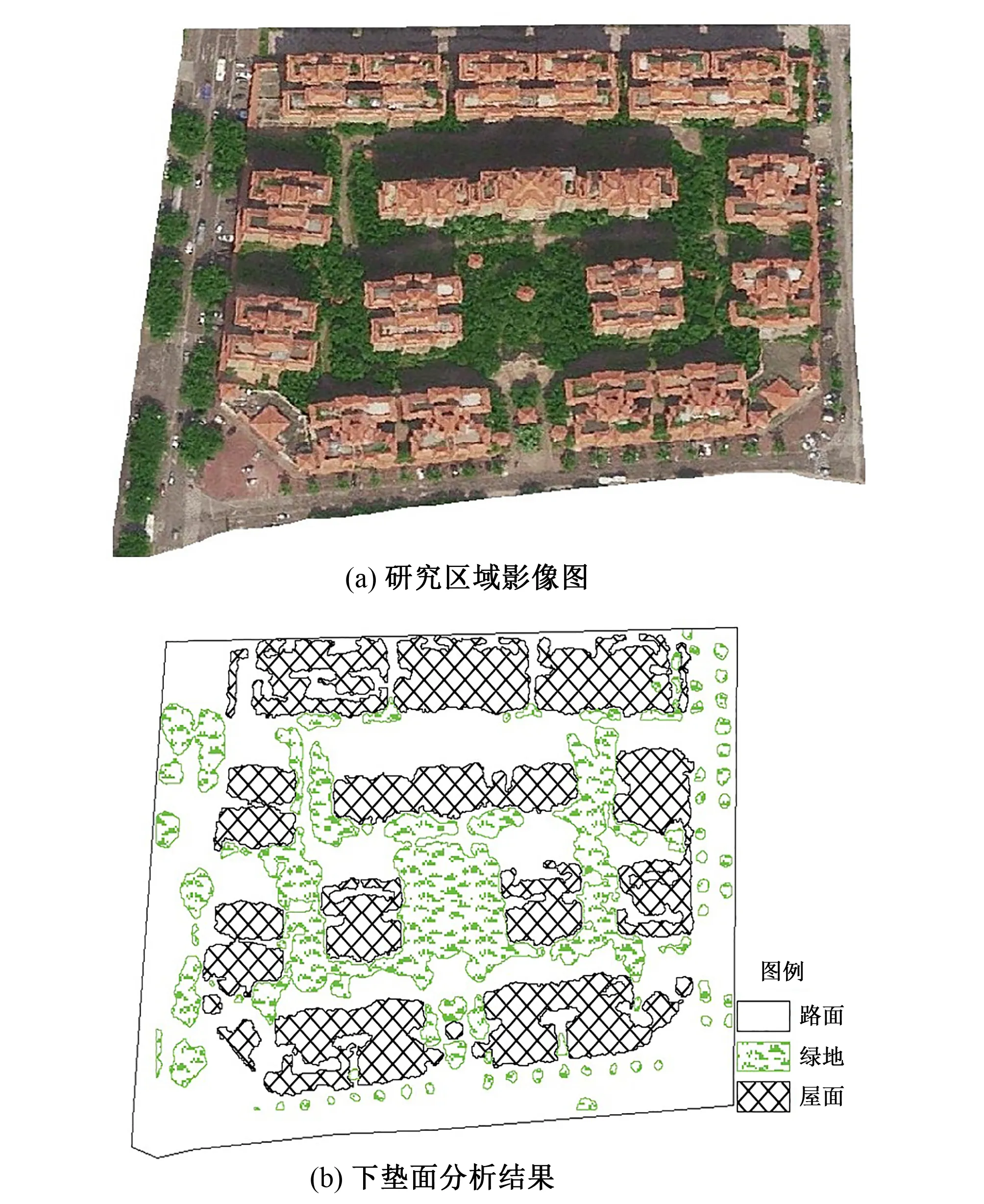
图1 研究区域下垫面分析

模型概化的过程主要包括模型中的节点、管线以及子汇水区的概化过程。模型概化后共包括21个节点，其中包括20个检查井和1个排放口，包括20根管渠以及27个子汇水区，子汇水区包括建筑屋面12个，广场2个，市政路面3个，小区路面10个。模型概化示意图及监测位置如图2所示。

图2 研究区域模型概化示意图

1.2 参数选择及取值

SWMM模型对降雨-径流过程的模拟主要包括地表产汇流和管道输水两个过程。本研究采用霍顿(Horton)渗透模型来描述透水地表产流过程，采用非线性水库法描述地表汇流过程，采用圣维南(Saint-Venant)方程进行管渠水流计算。

根据参数获取的方式，SWMM模型中参数分为可测量参数和不可测量参数。本文中可测量参数有节点底标高(Invert Elevation)、节点埋深(Max Depth)、子汇水区面积(Area)、管道长度(Length)、管道直径(Diameter)和子汇水区不透水比例(Pct-Imperious)，这6个参数通过资料收集或下垫面解析方法进行确定，在模型率定时固定可测量参数。不可测量参数则只能通过经验估计或者实测率定而进行获取，参考SWMM模型手册及相关文献[8,9]，表1给出了模型中不可测量参数的取值范围。

表1 SWMM不可测量参数及其取值范围

参数宽度修正因子Kwidth和坡度修正因子Kslope分别用于计算子汇水区的特征宽度及特征坡度：

(1)

式中：Area为子汇水区面积。

Slope=KslopeSlope0

(2)

式中：Slope0可以通过原有的地形图获取，作为识别特征坡度的初始取值。

1.3 Morris全局敏感性分析法

Morris法是一种基于筛选分析的全局敏感性分析方法[8]。其计算量较少，易于操作，并且该方法不会出现将重要参数遗漏的错误[9]，可用来筛选出那些不敏感的参数，从而保留敏感参数，这种定性筛选的作用正适用于本研究的研究目的。因此，本文采用Morris法对SWMM模型进行敏感性分析。一个典型的Morris设计图如图3所示，由图可看出Morris法是利用OAT(one factor at a time)的采样方法，即每次都只改变样本中的某一个参数。生成的样本在实际模拟计算的过程中映射到参数范围的分布之中，运行模型计算，设Y为模型的输出结果，则各个参数的基效应(Elemenary Effect，EE)为：

图3 Morris设计原理

(3)

式中：di(j)表示第i个参数第j组参数的基效应，j=1,2，…，r(r为重复次数)；Δ为第i个参数的扰动幅度。

通常表征Morris法的计算指标为“基效应的平均值”，公式如下：

(4)

参数的平均值表征参数的敏感性，平均值越大表明该参数对结果输出的影响越大，即越敏感，从而可以确定参数敏感性排序。

1.4 遗传算法

遗传算法是一种随机搜索和优化的方法，通过模拟大自然的生物进化过程，在种群不断进化过程中逐步淘汰不适应个体，而迭代中的种群进行不断交叉、重组、变异又能产生新的个体。遗传算法最重要的3个操作参数是：选择(Selection)、交叉(Crossover)、变异(Mutation)，可利用MATLAB中遗传算法工具箱函数完成该工作，本文中将运用MATLAB中遗传算法工具箱函数进行程序编写。

2 结果分析

2.1 Morris敏感性分析法计算结果

采用2016年7月10日实测降雨(73.6 mm)作为模型输入的边界条件，同时，本研究选取在城市降雨径流模拟中具有重要意义的3个输出变量：总径流量、峰值流量、峰现时间。敏感性计算结果如表2所示。

表2 各参数敏感性分析计算结果

对总径流量而言，敏感性排名前4的参数分别是Max Rate、Min Rate、Decay、N-Imperv，其他参数对径流总量的影响较小，这可能是因为在此场降雨条件下，管道曼宁系数Manning-N的取值基本对总径流量没有影响。对于流量峰值而言，敏感性排名前4的参数依次是Manning-N、N-Imperv、Kwidth、N-Perv，其他参数对峰值流量的影响均不大；对于峰值时间而言，其敏感性排序结果基本和峰值流量类似，敏感性排名前4的参数依次是Manning-N、N-Imperv、Kwidth、S-Imperv。

2.2 遗传算法步骤及计算结果

由前述敏感性分析可知，选取4个在对总径流量、峰值流量和峰值时间敏感性较高的参数作为率定参数，这4个参数是：Max Rate、Min rate、Manning-N、N-Imperv，参数的取值范围见表1。

利用MATLAB遗传算法进行参数率定的主要框架图如图4所示。

图4 遗传算法率定参数框架设计

算法具体计算步骤如下：

(1)随机产生初始种群。初始种群即父代种群，4个参数在各自的取值范围内构建一个解空间。控制matlab在该解空间中随机产生初始种群，本研究中所采用的初始种群数量为10个，即产生一个10行4列的初始参数矩阵，矩阵中每一行代表一个个体，也就是代表一组参数取值。

(2)输入监测数据。将该降雨场次下监测水深数据整理成可计算的数列变量输入matlab之中。

(3)由初始种群生成SWMM input文件。控制matlab将初始种群中的10组参数分别读写输入input文件中，使程序中产生10个可用于调用计算的SWMM input文件。

(4)在matlab中调用SWMM模型动态链接库(DLL)进行模型计算。由初始种群产生的10个input文件经过调用计算后，分别在相应的存储路径上产生10个report文件和10个output文件。其中report报告文件是对整个模型模拟过程的总结，以文本方式保存，output结果文件是在整个模拟过程中，各个元素在每个计算步长时的计算结果信息，例如节点水位、管道流量、子汇水区流量等，以二进制方式保存。

(5)读取SWMM report文件将所需计算结果存入matlab之中。读取模型计算后report文件中对应计算结果值，提取与监测数据时刻对应的结果，将其整理成可计算的数列变量输入matlab之中。

(6)计算目标函数值。目标函数是用于评价计算模拟值与监测数据值吻合程度的函数。本文中选用Nash-Sutcliffe效率系数作为目标函数，可以用作考察模型计算的准确程度[9]。Nash-Sutcliffe效率系数的计算公式为：

(5)

(7)分配初始种群适应度函数。根据种群中各个个体的目标函数值，对初始种群适应度进行排序，目标函数越大则个体适应度值也越大，并将排序结果写入对应的个体适应度值的列向量。

(8)选择交叉变异产生子代。由上一步所得的个体适应度列向量作为选择依据，适应度值越大的个体被选中作为下一代的概率越大，相反，适应度值小的个体被选中的概率会很小。调用遗传算法工具箱中选择函数，从初始种群中选择优良个体，并将选择的个体写入下一代种群之中。

调用遗传算法工具箱函数recombin从产生的新种群中完成交叉，采用单点交叉xovsp函数，使用交叉概率Px=0.7执行交叉，并将执行交叉后的个体写入新种群之中。

调用遗传算法工具箱函数mutbga对该种群进行实值变异，使用变异概率Pm=0.05执行变异，并将执行变异后的个体写入新种群之中。

(9)控制matlab将所产生的子代种群(参数矩阵)输入SWMM input文件中并保存。由初始种群经过选择交叉变异后产生子代参数矩阵，控制matlab进行文本文件的读写，将对应的参数值修改并写入input文件中，将input文件保存并用于下一步的计算。

(10)循环运行4～9步直至满足迭代满足要求，本文中采用最大迭代次数500为迭代结束条件。

毎代种群最优解和种群均值变化跟踪图如图5所示。实线代表每个迭代种群中目标函数的最大值，虚线表示迭代次数中种群均值的变化过程。从图5中可以看出，初始种群的目标函数平均值在0.5以下，在迭代计算前120次左右时，种群最优解和种群均值变化曲线有着显著上升，为了防止目标函数解落入局部最优，迭代继续进行，在随后的迭代计算中，即使有重组变异的过程使得种群目标函数均值处于波动状态，但种群最优解处于稳定状态，可以认为遗传算法在此次寻优的过程之中找到了全局最优解。第500次迭代的结果为： Max Rate为50.25， Min Rate为12.61， Manning-N为0.018 2，N-Imperv为0.008 7。

图5 500次迭代后种群最优解与种群均值变化跟踪图

此时目标函数最大值为0.726 1，也就是此时经计算后的Nash-Sutcliffe效率系数为0.726 1。当计算结果NS值越接近于1，表示模拟值与观测值越接近，说明模型的计算准确度越高。参考相关的文献[9]可知，当计算的NS效率系数大于0.7时，近似的认为模拟结果与实测结果的吻合程度较高，模型误差在计算误差允许的范围内。因此可以认为本次模型参数率定过程与实测结果吻合程度较高，模型计算结果与实测数据对比如图6所示。

图6 参数率定后计算结果与实测数据对比图

3 结 语

(1)本文该场次降雨下参数敏感性分析结果表明，霍顿渗透参数对输出目标总径流量敏感性最大，管道曼宁系数对输出目标峰值流量和峰值时间敏感性最大；

(2)选取4个敏感参数进行率定，遗传算法结果表明，Max Rate为50.25，Min Rate为12.61，Manning-N为0.018 2，N-Imperv为0.008 7，该场降雨下目标函数NS值为0.726 1。

(3)通过MATLAB调用SWMM进行水力计算来实现模型自动率定功能，充分利用SWMM模型的水力计算和MATLAB的数据分析功能，实现模型自动率定。该方案及编程可以应用于实际工程的参数率定过程，并得出与实测结果最接近的参数组合，提高了模型模拟的精度及稳定性。