基于灰色系统的太平洋褶柔鱼秋生群资源丰度灾变预测

张磊，陈新军，汪金涛*，吴洽儿

(1.上海海洋大学 海洋科学学院，上海 201306； 2.中国水产科学研究院南海水产研究所，广东 广州 510300； 3.农业农村部大洋渔业开发重点实验室，上海 201306； 4.国家远洋渔业工程技术研究中心，上海 201306； 5.大洋渔业资源可持续开发教育部重点实验室，上海 201306；6.农业农村部大洋渔业资源环境科学观测实验站，上海 201306)

近几十年来，头足类渔业在全球渔业中开始取代传统经济鱼类并占据重要地位[1]。太平洋褶柔鱼Todarodespacificus属温带大洋性经济头足类[2-3]，是世界头足类中最早被大规模开发利用的种类之一[4]，主要分布在西北太平洋21°～50° N海域，日本海、日本太平洋沿岸及中国黄海、东海为主要的作业渔场[5]。根据太平洋褶柔鱼的产卵季节可分为夏生群、秋生群和冬生群3个种群，其主要捕捞群体为秋生群和冬生群[6-8]。目前，秋生群的主要捕捞区域在日本海，日本和韩国的渔获量最高。

近年来，太平洋褶柔鱼的捕捞产量波动较大，由于环境因素对短生命周期生物的影响明显，且这一影响可能超过捕捞影响[9]，因此，造成太平洋褶柔鱼资源量波动现象可能是由于栖息环境中的海温等环境因子的变化。目前，已有学者将太平洋褶柔鱼的渔业数据和环境数据结合，对其中心渔场和资源丰度等进行预报[10-11]。吴梦瑶等[4]选择平均海表面温度(sea surface temperature，SST)作为环境因子，用剩余产量模型(Schaefer模型和Fox模型)对太平洋褶柔鱼渔获量进行预测。武胜男等[1]利用交相关法分析了厄尔尼诺、太平洋年代际涛动、产卵场SST、叶绿素浓度(chlorophyll a, Chl-a)及最适产卵温度范围占产卵场总温度范围的比例(Ps)与太平洋褶柔鱼秋生群资源丰度的相关性。解明阳等[2]采用灰色系统中的灰色关联分析方法对影响太平洋褶柔鱼冬春群资源丰度的环境和气候因子进行分析，并利用灰色预测GM(1，N)模型建立太平洋褶柔鱼冬春群资源丰度预测模型。上述研究均将环境因素作为影响因子加入，然而在缺乏可靠的预报环境因子的情况下，如何利用仅有的捕捞数据进行较为准确的分析，也值得学界深入研究。

灰色年灾变预测属于灰色系统理论的一个分支，其实质是通过对单一数据中异常值进行分析，预测下一个或几个异常值出现的时间，研究者就可以通过下一次异常出现的时间，采取相应的措施。灰色系统理论是一门不确定的系统理论学科，具有所需样本数据少、不需要计算统计特征量等优点，因此，被广泛应用于许多领域[12]，如灰色数列预测、灾变预测、季节性灾变预测、系统预测等[13]。这对于缺乏数据的渔业科学来说，具有较大的应用前景[14]。目前，国内外学者利用灰色系统在渔业资源丰度与资源量预测[15-17]、渔业产量预测[18-19]等方面均取得了比较好的效果。也有学者应用灰色系统理论对鳗鲡苗种丰谦年进行灾变预测，并取得了较为准确的预测结果[20]。

本研究中，利用灰色年灾变预测GM(1，1)模型分析日本海和东海海域太平洋褶柔鱼秋生群1990—2014年单位捕捞努力量渔获量变化趋势，科学预测这一海域太平洋褶柔鱼秋生群丰歉年份，指导相关渔业企业进行生产作业投入控制，为管理部门制定相关管理办法提供参考依据。

1 材料与方法

1.1 渔业数据

本研究中渔业数据来自日本海海洋渔业研究所《平成29(2017)年太平洋褶柔鱼秋生群落资源评估报告》， 1985—2014年日本海和东海海域太平洋褶柔鱼秋生群资源单位捕捞努力量渔获量(catch per unit effort，CPUE)[21]。太平洋褶柔鱼秋生群资源单位捕捞努力量渔获量根据捕捞报告中的日本海(5—10月)和东海(5—11月)的总捕获量/总天数计算得出(单位：t/d)(图1)。

图1 1990—2014年日本海(5—10月)和东海(5—11月)太平洋褶柔鱼单位捕捞努力量渔获量Fig.1 Catch per unit effort of pleated squid Todarodes pacificus in the Sea of Japan (May to October) and the East China Sea (May to November) from 1990 to 2014

1.2 方法

灰色年灾变预测即根据灾变日期集，建立预测模型预测灾变日期，通过已知的“量”来求未知的“时”，是预测异常值或“灾变”点出现的时间[22]。利用灰色灾变预测GM(1，1)模型预测未来太平洋褶柔鱼秋生群出现的丰年和歉年。具体建模过程如下[23]。

先取太平洋褶柔鱼秋生群单位捕捞努力量渔获量作为原始数据列，即

X(0)(t)={X(0)(1)，X(0)(2)，…，

X(0)(n)}。

(1)

规定一个灾变阈值ξ，以X(0)(t)中大于ξ值(上灾变)或小于ξ值(下灾变)的数为灾变阈值，分别选出来组成一个新的数据序列，同时以这组数据中各个数据出现的对应时刻,组成灾变时刻序列(日期集)，即

D(0)(t)={D(0)(1)，D(0)(2)，…，

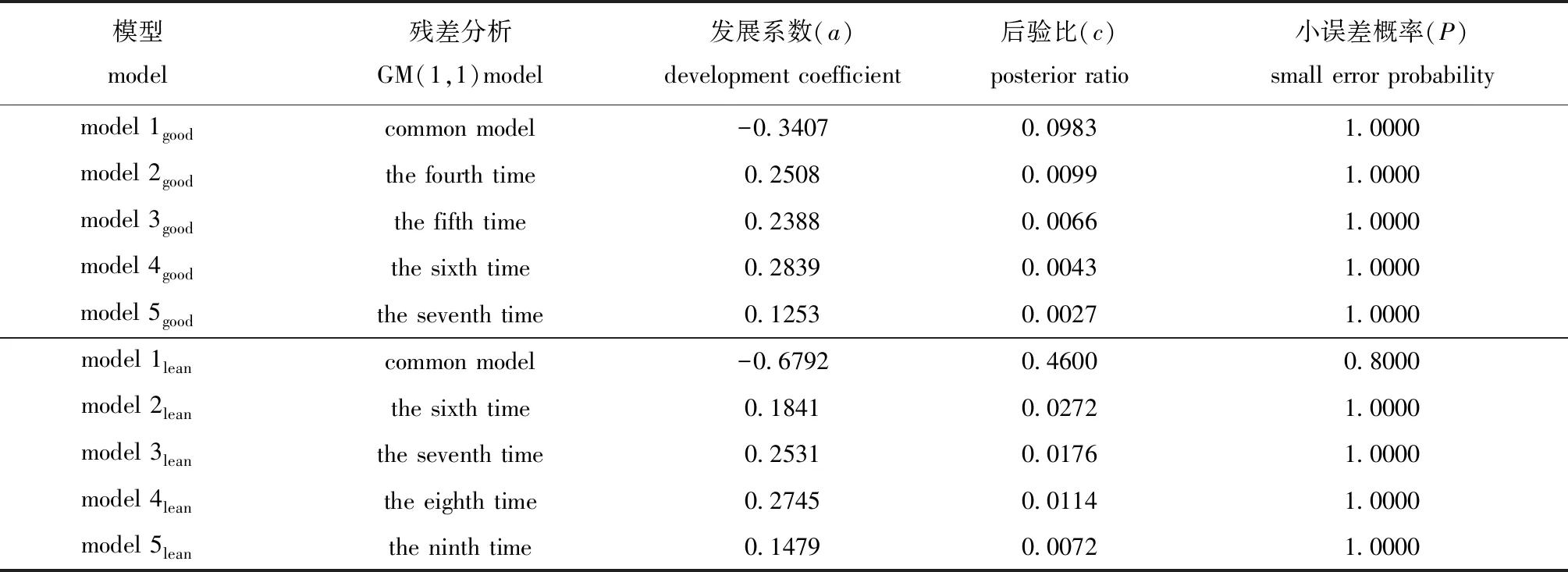
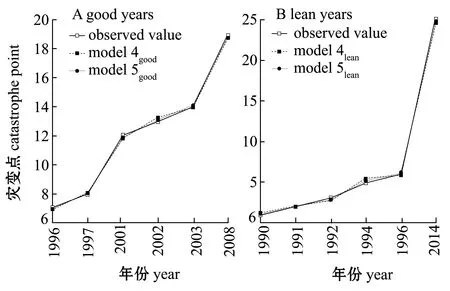
D(0)(n)} (n

(2)

之后再将D(0)(t)数据序列进行累加，代入灰色灾变预测模型，进行模型诊断。采用后验比c(表1)和小误差概率P对模型预测精度进行检验，当P>0.95和c<0.35时，则模型合格，可用该模型对太平洋褶柔鱼秋生群资源丰度进行灰色灾变预测，且当|a|<0.3时，该模型可用于中长期预测。若原始数据分析残差较大，精度不够理想时，为提高精度，需对其残差进行残差GM(1,1)模型建模分析，修正预报模型。根据最终模型对太平洋褶柔鱼秋生群资源丰度进行丰谦年的灾变预测。

表1 灰色系统理论模型精度检验等级

2 结果与分析

2.1 残差分析和最优模型的验证

前期研究表明，CPUE可作为太平洋褶柔鱼资源丰度指标[21]。先取定太平洋褶柔鱼秋生群CPUE作为原始数据列，取其上四分位和下四分位分别作为丰年和歉年的阈值ξ，分别为2.895和2.149。即当某一年份的CPUE数值大于2.895，设置为丰年；当某一年份的CPUE数值小于2.149，设置为歉年。根据阈值设置 1990—2014年太平洋褶柔鱼秋生群资源丰度丰歉年，根据残差分析最终获得太平洋褶柔鱼秋生群资源丰度的丰年灾变预测模型5个，即model 1丰、model 2丰、model 3丰、model 4丰、model 5丰，歉年灾变预测模型5个，即model 1歉、model 2歉、model 3歉、model 4歉、model 5歉)。其预测模型各参数如表 2所示。

根据表1的模型精度检验等级参照表可知，本研究中构建的太平洋褶柔鱼秋生群资源丰度丰年灰色灾变预测模型中，其后验比c值均小于 0.35，小误差概率P值均大于 0.95，歉年灰色灾变预测模型中，其后验比c值除了普通 GM(1,1)模型(model 1歉)外均小于0.35(表2)，模型均通过检验，均为一级精度等级模型，可用于预测太平洋褶柔鱼秋生群资源丰度的丰歉年份。

若预测模型中的发展系数|a|<0.3，则该模型可用于中长期预测。丰年灰色灾变预测5个模型中，除普通 GM(1,1)模型(model 1丰)外，其余4个模型均为|a|<0.3，均可用于对太平洋褶柔鱼秋生群资源丰度的丰年中长期预测;在歉年灰色灾变预测5个模型中，除普通 GM(1,1)模型(model 1歉)外，其余4个模型均为|a|<0.3(表2)，这4个模型均可用于对太平洋褶柔鱼秋生群资源丰度的歉年进行中长期预测。

表2 丰、歉年灰色灾变预测模型参数Tab.2 Parameters of gray catastrophe prediction model in good years and lean years

根据表2可知，符合要求的丰、歉年预测模型间无显著性差异。因此，按残差最小化原则，丰年模型选取第6次、第7次残差分析，歉年模型选择第8次、第9次残差分析(图2)。

2.2 丰歉年灾变模型预测结果

太平洋褶柔鱼秋生群资源丰度的灾变预测结果均取model 4、model 5的预测。从表3可知，自2014年后，出现超过上灾变点阈值的3个点对应的序号分别是31、45、63，即未来太平洋褶柔鱼秋生群资源丰度出现丰年的年份分别为2020、2034、2052年；自2014年后，出现低于下灾变点阈值的3个点对应的序号分别是78、136、283，即未来太平洋褶柔鱼秋生群资源丰度出现歉年的年份分别为2067、2125、2272年。

表3 太平洋褶柔鱼秋生群资源丰度丰、歉年灰色灾变模型预测结果

3 讨论

3.1 日本海和东海海域太平洋褶柔鱼秋生群资源预测

本研究中基于灰色系统对日本海和东海海域太平洋褶柔鱼秋生群资源丰度进行灾变预测，对太平洋褶柔鱼秋生群1990—2014年的资源丰度数据进行到目前为止，2008年是该海域太平洋褶柔鱼秋生群资源出现的最后一个丰年年份，从已知的2008年到2014年太平洋褶柔鱼秋生群资源丰度中可以看出，太平洋褶柔鱼秋生群的捕捞量已经趋于稳定状态，有缓慢下降趋势，到2014年出现了歉年。吴梦瑶[4]基于海表面温度建立剩余产量模型发现，2014年温度整体低于太平洋褶柔鱼胚胎最适温度，资源生物量减少，导致产量降低，出现了歉年。另外，还可能包括气候因子，如太平洋年代际震荡指数PDO(Pacific decadal oscillatio index)、厄尔尼诺指数Nino3.4距平、黑潮强弱指数KCA(Kuroshio current average) 、平均叶绿素浓度Chl-a(average chlorophyll aconcentration)等[2]，本研究中仅对出现丰歉年的年份进行预测，具体的影响因素还需结合当年的环境、气候因子进行分析。下一次出现丰年的时间为2020年，而自2014年出现歉年后，再次出现歉年的日期为2067年。这说明日本海和东海海域太平洋褶柔鱼秋生群的产量在缓慢下降后又会有一个逐步升高的过程，并在之后的几十年中均处于一个相对稳定的状态。

注：model 4good为第6次残差GM(1,1)模型；model 5good为第7次残差GM(1,1)模型；model 4lean为第8次残差GM(1，1)模型；model 5lean为第9次残差GM(1，1)模型Note: model 4good, sixth residual GM(1,1) model; model 5good, 7th residual GM(1,1)model；model 4lean, eighth residual GM (1，1) model; model 5lean, ninth residual GM (1，1) model图2 2种丰年和2种歉年灰色灾变模型验证结果Fig.2 Validation results of gray catastrophe model for 2 types of good years and 2 types of lean years

3.2 GM(1，1)模型的优、劣势及未来研究方向

通过对日本海和东海海域太平洋褶柔鱼秋生群1990—2014年的单位捕捞努力量渔获量原始数据的处理，并应用灰色灾变系统对未来可能出现的丰歉年份进行预测，其预测值只是一个灰区间，且此灰区间会随样本长度大小、样本起始点的不同发生变化，从而导致预测值发生改变。因此，利用灰色系统进行年份灾变预测时需注意数据序列的长度，序列太短可能导致信息太少，不具有普遍性，导致结果失真，但序列太长又难以满足灰色系统要求的数列应满足光滑性，也会导致预测失败。

如果进行多种影响因子预测可能更有说服力，但是目前大范围的叶绿素浓度、海表面温度都是卫星遥感数据，遥感数据的实时性、完整性可能会受多种因素的影响，不能满足渔业预报对数据及时性和完整性的要求。

本研究中仅对日本海和东海海域太平洋褶柔鱼秋生群资源丰度进行了丰歉年的灾变预测。太平洋褶柔鱼资源量还会受到栖息环境、捕食者情况等的影响，若要更加准确地预测其资源丰度，还可使用灰色系统的其他模型结合更多的因素来预测，建立更加全面、科学、可靠的预测模型，为该海域太平洋褶柔鱼或其他海洋鱼类的开发、利用提供科学依据。