空气不耦合装药孔壁初始冲击压力的计算

张恒根，王卫华，王永强

(中南大学资源与安全工程学院，长沙 410083)

在确定不耦合装药系数等爆破参数时，孔壁初始冲击压力是重要的依据之一，对它的研究吸引了众多学者的注意。在以往的研究中，有些学者主张利用计算爆轰产物压力的方法得到不耦合装药时的孔壁压力，如费鸿禄等[1]以爆轰气体动力学及岩石断裂理论为基础，推导了装药不耦合系数的计算公式。宗琦等[2]将爆生气体膨胀充满炮孔时的准静压力作为孔壁初始压力，得到了空气垫层装药结构轴向不耦合系数的计算方法。也有学者主张利用计算冲击波压力的方法得到不耦合装药时的孔壁压力，如朱红兵等[3]利用冲击波理论分析了空气间隔装药炮孔内压力波的传播过程，得到了合理空气层比例的确定方法。陈明等[4]推导了爆炸冲击波与弹性壁碰撞后压力增大倍数的理论解，提出了轮廓爆破孔壁压力峰值的计算模型。杜俊林等[5]利用冲击波的基本关系式计算了空气不耦合装药时的孔壁压力。还有学者用模拟及实验等其他方法对孔壁压力进行了研究，如王志亮等[6]对水不耦合装药爆破进行了数值模拟，分析了孔壁压力与不耦合系数之间的关系。V.R.Feldgun等[7]对爆破荷载的变化过程进行了数值模拟，并与实验结果进行了分析对比。凌伟明[8]采用锰铜压阻传感器进行了孔壁压力测量的实验，验证了锰铜压阻传感器用于测试孔壁压力的可行性。刘云川等[9]按照能量等效原则，给出了径向不耦合装药条件下炮孔初始压力的计算公式。楼晓明等[10]引入St-arfield迭加法，分析得到了上部空气间隔装药和中部空气间隔装药条件下孔壁初始冲击压力的计算公式。众多其他学者[11-14]也研究了孔壁初始冲击压力问题，提出了许多计算孔壁压力的方法。

目前常用的计算不耦合装药孔壁初始冲击压力的方法是,先计算爆轰产物在炮孔内做等熵膨胀后作用于孔壁的准静压力，然后将准静压力乘以压力增大系数n，近似得到了孔壁岩石所受到的初始压力。n一般取8～11。爆轰产物在炮孔内的膨胀可以按照一阶段或两阶段等熵膨胀计算[15]。当不耦合系数比较小时，通常按照一阶段等熵膨胀计算：

(1)

当不耦合系数比较大时，按照两阶段等熵膨胀计算：

(2)

式(1～2)中：pt为透射入孔壁的初始冲击压力；ρw为炸药的密度；D为爆轰波波阵面的速度；R为炮孔半径；r为药卷半径；pk为两阶段交接点处的临界压力，中等威力的硝铵类炸药pk一般取2.0×108Pa。

上述常用公式在理论上并不严密，其计算结果与实测值往往相差较大。以往对于不耦合装药孔壁初始冲击压力计算方法的研究始终围绕着不耦合装药的破岩机理，即由冲击波破岩和爆生气体破岩的理论展开。由于确定爆破近区空气冲击波衰减和爆生气体膨胀规律的困难性，以及爆轰波、空气冲击波与孔壁之间相互作用的复杂性和测试系统的局限性等原因，致使空气不耦合装药条件下孔壁初始冲击压力较难确定。以往利用计算爆轰产物压力的方法计算孔壁压力时，往往事先假定忽略炮孔内空气层的存在，进而忽略空气冲击波对孔壁的影响，这与事实不符，因为利用计算冲击波压力的方法确定孔壁压力时，往往将孔壁面作弹性面简化处理，且较少考虑空气冲击波传播过程中的衰减。作者在前人研究的基础上，通过分析不耦合装药爆轰后冲击波作用于孔壁的物理过程，建立了空气冲击波在炮孔内衰减传播模型，利用该模型计算了空气冲击波对孔壁的入射压力，再利用空气冲击波正入射时的界面处连续条件，获得了孔壁初始冲击压力的计算公式，并将计算结果与常用公式的计算值、模拟值和实验结果进行对比分析。

1 物理过程

为了比较合理地确定孔壁初始压力，首先要清楚爆轰后冲击波作用于孔壁的物理过程。空气不耦合装药爆轰后，空气冲击波随时间变化作用于孔壁的过程如图1所示。

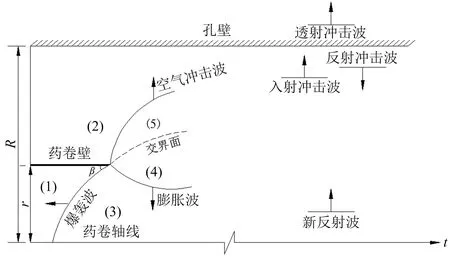
注：(1)区为未爆轰的药卷；(2)区为炮孔内的空气层；(3)区为爆轰后还未膨胀的爆轰产物；(4)区为受膨胀波扰动后开始膨胀的爆轰产物；(5)区为空气冲击波过后被压缩的空气。图1 空气冲击波随时间变化作用于孔壁的过程Fig.1 The process of air shock wave acting on the hole wall with time

当柱状药卷(1)孔底起爆时，爆轰波以半球面波的形式自药卷底部向孔口方向传播。爆轰波的波阵面在药卷壁处以较小的倾斜角度β猛烈地撞击药卷周围(2)区内的空气，并在接触空气的瞬间产生反射和透射。这个倾角β即为爆轰波对空气介质的入射角，由于入射角很小，可以近似地认为爆轰波以正入射的方式接触药卷周围的空气。由于爆轰波后(3)区内爆轰产物的冲击阻抗远大于(2)区内空气介质的冲击阻抗，因此爆轰波在空气介质处的反射波为一膨胀波，反射的膨胀波可以理想化为经由(3)区内还未膨胀的爆轰产物向药卷中心轴线上传播的半径不断缩小的柱面波，受膨胀波的扰动，(3)区内未膨胀的爆轰产物即开始膨胀。膨胀波的波阵面最终汇聚于药卷中心的轴线上，并且在轴线上产生一个在(4)区内已经膨胀的爆轰产物中向外传播的新反射波。爆轰波透射形成的空气冲击波经(2)区内的空气层向孔壁传播，由于压缩(5)区内的空气散失能量致使空气冲击波在空气层中传播时，其峰值压力和波阵面的速度会逐渐衰减。最后，衰减后的空气冲击波会以正入射的方式作用于孔壁岩石上，产生反射和透射。由于岩石的冲击阻抗远大于(2)区内空气介质的冲击阻抗，因此空气冲击波在孔壁处的反射波仍为冲击波，反射的冲击波同样可以理想化为经由(4)区内已经膨胀的爆轰产物向炮孔中心轴线上传播的半径不断减小的柱面波，并在其波阵面汇聚于炮孔中心的轴线上后向外传播一个新的反射波。由于这个新的反射波在爆轰产物中传播时，气态爆轰产物已经迅速膨胀，充满了整个炮孔，故可以认为在爆轰气体接触孔壁之前，爆轰扰动空气产生的空气冲击波在孔壁的透射冲击波参数即为孔壁初始冲击参数。

2 衰减规律

爆轰扰动空气形成的初始空气冲击波以柱面波的形式向孔壁传播，由于柱面半径的增大，其波阵面单位面积上的能量将不断减少，被压缩后的空气由于熵值的增大，会将部分动能不可逆的转化为热能，这些能量的散失致使空气冲击波在到达孔壁时，其峰值压力和波阵面的速度已迅速下降，另外随着冲击波宽度的增加，对空气的正压作用时间也不断加长。

空气冲击波在炮孔空气层中衰减传播的计算模型如图2所示，其中Da、pa、μa、ρa分别表示空气冲击波在炮孔内传播距离为x时波阵面的速度、压力、质点移动速度和密度；p0、ρ0、μ0分别表示空气冲击波前未受扰动的空气的压力、密度和质点移动速度。未受扰动的空气处于静止状态，μ0=0，ρ0=1.2 kg/m3。

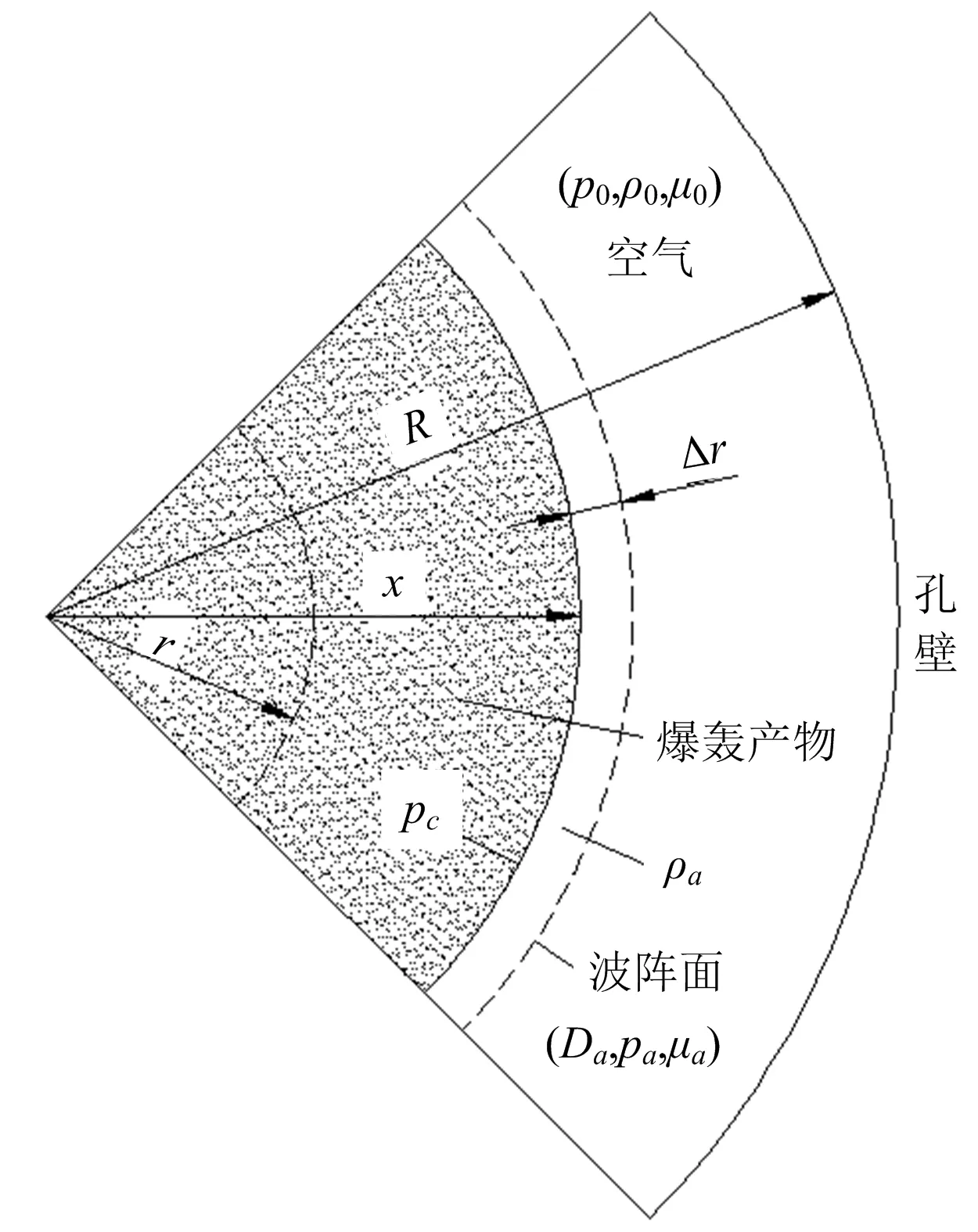
图2 空气冲击波在炮孔空气层内衰减传播模型Fig.2 Attenuation propagation model of air shock wave in the air layer of blasthole

假定当空气冲击波在炮孔内的传播距离为x时，途经的空气受其扰动，质量全部集中于波阵面附近厚度为Δr的薄层之中。由于空气冲击波波阵面的压力pa很强，波前静止空气的压力p0可以忽略，于是空气冲击波满足强冲击波的基本关系式[16]如下：

(3)

(4)

(5)

式中：k为绝热指数，一般取1.3。

(6)

(7)

式中：pw为爆生气体的平均爆轰压力，pw=ρwD2/2(γ+1)；Vw为装药体积，Vw=πr2l，l为炮孔长度，装药系数为1；Vk为爆生气体压力为pk时的体积；px为爆生气体膨胀到距药卷中心x处时的平均压力；Vx为爆生气体压力为px时的体积，Vx=πx2l。

由界面条件可知，在薄层与爆生气体的交界处，界面两侧的压力相等，则

(8)

令pc等于波阵面压强pa的θ倍，对薄层内的空气应用牛顿第二定律，得

(9)

式中：m为被空气冲击波所席卷的空气的质量，m=π(x2-r2)lρ0。

将式(3)和式(4)代入式(9)化简得

(10)

可以将上式写为

(11)

对两边积分得Da=A(x2-r2)θ-1，其中A为积分常数。

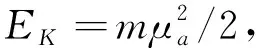
(12)

单位质量的理想气体，其内能为

e=pν/(k-1)

(13)

式中：p和ν分别表示气体的压力和比容。

假设空气薄层内压力呈线性变化，则薄层内空气的内能ET为

(14)

将式(4)和式(5)代入式(14)并替换掉m和Da可得

(15)

爆炸传递给冲击波的总能量EO为

(16)

在对爆轰扰动空气形成的初始冲击波参数的计算过程中可以发现，空气冲击波的传播速度要大于爆轰产物的喷流速度[15]，故可以认为空气冲击波对空气的裹挟要快于爆轰产物膨胀对空气的压缩，进而认为爆轰产物在膨胀到孔壁前为自由膨胀，对炮孔内的空气做功为零。爆轰传递给冲击波的总能量EO为一定值，即EO为与x无关的常数，故

2θ-1=0

(17)

得θ=1/2。

借助于式(8)求得的pc值，可以计算出当空气冲击波传播到孔壁时，即当x=R时，空气冲击波对孔壁的入射压力pa为

(18)

利用强冲击波的基本关系式和pa值可得,当空气冲击波传播到孔壁时，入射空气冲击波波阵面的速度Da和质点移动速度μa分别为

(19)

(20)

将式(16)变换后代入Da=A(x2-r2)θ-1，并化简得

(21)

将式(21)代入式(3)和式(4)可得

(22)

(23)

由式(21)～(23)得到空气冲击波参数随传播距离的衰减关系(见图3～图4)。

图3 空气冲击波波阵面速度和质点移动速度随传播距离的衰减Fig.3 Attenuation of wave front velocity and particle moving velocity of air shock wave with propagation distance

图4 空气冲击波波阵面压力随传播距离的衰减Fig.4 Attenuation of wave front pressure of air shock wave with propagation distance

从图3和图4可以看出，空气冲击波在炮孔内空气层中传播时，波阵面的速度、压力和质点移动速度会随传播距离的增加呈指数型衰减，波阵面压力的衰减速度要比波阵面速度和波阵面质点移动速度衰减的快。空气冲击波参数的大小与爆炸传递给冲击波的总能量和药卷长度之间存在线性关系，爆炸传递给冲击波的总能量越强，则冲击波的参数越大。空气冲击波的衰减规律如下：

(24)

3 初始参数计算

空气冲击波传播到孔壁时即产生反射和透射，在求解透射波的初始参数时，以往的研究中多将孔壁面作为弹性面处理，认为透射波是直接以应力波的形式在孔壁岩石中传播的，进而应用弹性理论求解孔壁的初始冲击压力[16]。实际上，空气冲击波正入射孔壁之后，在已经膨胀的爆轰产物中传播的反射波和在孔壁岩石中传播的透射波均为冲击波，且反射冲击波和透射冲击波波阵面的压力会因岩石波阻抗的增大而大于入射空气冲击波波阵面的压力。空气冲击波在孔壁处的压力变化如图5所示。

注：pa，μa分别表示空气冲击波传播到孔壁时波阵面的压力和质点速度；pt，μt分别表示在孔壁岩石中传播的透射冲击波波阵面的压力和质点速度；μs表示反射冲击波波阵面的质点速度，其与空气冲击波的传播方向相反；pr，μr，ρr分别表示透射冲击波前未受扰动的岩石的压力、质点速度和密度。图5 空气冲击波在孔壁处的透、反射Fig.5 The transmission and reflection of the air shock wave at the hole wall

未受扰动的岩石处于静止状态，μr=0。空气与岩石交界面两侧质点的移动速度是相等的，因此在交界面上有

μt=μa-μs

(25)

对反射冲击波应用冲击波后质点速度方程可得

(26)

式中：ca，ct分别为反射冲击波波前和波后介质的比容。

反射冲击波的冲击绝热线可以写为

(27)

将式(26)和式(27)代入式(25)可得

(28)

将式(18)和式(20)以及ca=(k-1)/(k+1)ρ0代入式(28)可得

(29)

对在岩石中传播的透射冲击波可用冲击波后的质点速度方程计算，由于pt≫pr，方程中的pr可以忽略，得

(30)

式中：ρt为受透射冲击波扰动后岩石的密度。

岩石的状态方程为[17]

(31)

式中：Cr为未受扰动的岩石中的纵波波速；B为常数。

当炸药的密度ρw，爆速D，炮孔半径R和药卷半径r已知时，由式(18)和式(29)～式(31)即可求得孔壁初始冲击压力pt。

4 结果对比与讨论

文献[8]采用锰铜压阻传感器实验测量了水泥砂浆试件在空气不耦合装药条件下的孔壁压力，文献[12]利用ANSYS/LS-DYNA软件对文献[8]中的实验模型进行了数值模拟。采用文献[8]中的岩石和炸药参数以及不耦合系数，炸药密度ρw=1.0 g/cm3，爆速D=3 200 m/s，水泥砂浆试件未受扰动时的密度ρr=2.2 g/cm3，纵波波速Cr=3 200 m/s，压力增大系数n取8，炮孔直径40 mm，分别代入2个常用公式和本文推导的方程组中计算孔壁初始压力，将计算结果与文献[8]的实测值及文献[12]的模拟值共同绘制于图6中。

图6 本文计算结果与模拟值、实测值的比较Fig.6 Comparison of calculated results with simulated and measured values

从图6可以看出，用本文推导方程组计算的孔壁初始压力比常用公式的计算值和模拟值更接近于实测值。当不耦合系数为1.14时，方程组计算的孔壁初始压力，与实测值误差为8%；当不耦合系数为1.6时，误差为21%，均小于模拟值和常用公式计算值相对于实测值的误差。方程组计算值与实测值随不耦合系数变化的趋势也较为一致。数值模拟的结果与实测值相比，可靠度为80%左右[12]。

常用公式的计算结果比实测值小很多。常用公式依据冲击波在炮孔壁的透、反射致使孔壁入射压力增强的观点得出，计算时将爆生气体的准静态压力作为冲击波对孔壁的入射压力，理论上并不严密。其中n的取值直接影响到孔壁压力的计算值。n的取值与装药结构、炸药特性和岩体介质等多种因素有关，且应当随不耦合系数的变化而变化，因此想要比较合理的确定n值是比较困难的[4]。

如果在方程组的推导过程中将爆生气体在炮孔内的膨胀按照一阶段的等熵膨胀计算，则此时用方程组计算的孔壁入射压力值即为爆轰波波阵面的压力，可得到耦合装药时孔壁压力的计算方程组，其与文献[11]中推导的耦合装药时岩体中爆炸冲击波参数的计算公式一致。

文献[18]利用弹性波动理论得出了耦合装药时透射波初始压力的计算公式为

(32)

将文献[8]中的岩石与炸药参数代入式(32)计算得耦合装药时的孔壁压力为3.52 GPa，与实验值和模拟值相差较大。方程组计算的耦合装药时的孔壁压力为8.14 GPa，与实验值误差仅为4.5%，远小于模拟值和式(32)计算值较实验值的误差。

笔者在求解薄层内侧压力时，假设爆生气体内压力均匀分布，这样会导致当不耦合系数较小时，计算的空气冲击波对孔壁的入射压力值偏大，从而使孔壁压力计算值偏大。其原因是当不耦合系数较小时，炮孔内孔隙较小，爆生气体的膨胀空间有限，将爆生气体内压力做均压处理会使计算的入射冲击波压力增大，导致计算的孔壁压力值偏大。

5 结论

1)空气不耦合装药时，爆轰扰动形成的空气冲击波在炮孔内的空气层中传播时，波阵面的速度、压力和质点移动速度会随距离的增加呈指数型衰减。

2)空气不耦合装药时孔壁初始冲击压力会随装药不耦合系数的增大先迅速减小后趋于稳定值。

3)与经验公式计算值和模拟值相比，本文推导方程组的计算值较实验值误差更小。如果将爆生气体的膨胀作一阶段等熵膨胀考虑时，该方程组也能较好的计算耦合装药时的孔壁压力。