爆炸荷载作用下覆土库外部冲击波传播规律

荣 凯，杨 军，董文学，唐红亮，崔 宁

(1.北京理工大学爆炸科学与技术国家重点实验室，北京 100081；2.中国兵器工业火炸药工程与安全技术研究院，北京 100053)

覆土库是库体结构表面覆盖土的危险品仓库，一般用于存储火炮、弹药及军用武器等。覆土库由于其独特的结构特点，在受内部爆炸荷载作用下，对冲击波的传播具有一定的导向性。目前，许多学者对覆土库及其他建筑结构在内部和外部爆炸冲击波荷载作用下的动态响应以及冲击波的传播规律进行了研究。

在受爆炸冲击波荷载作用下结构动态响应的研究方面，Yong Lu等[1]、洪武等[2]采用非线性动力学有限元软件ANSYS/LS-DYNA对地下混凝土结构受外部爆炸荷载作用下的动态响应进行模拟，比较了三维模型和二维模型模拟所得冲击波峰值压力和结构加速度等参数，得出了结构的动态响应规律以及冲击波的传播过程。康婷等[3]采用数值模拟的方法对地下拱形结构受外部爆炸荷载作用下的动态响应进行研究，将结构的动态响应划分为4个阶段，得出了不同阶段结构动态响应能量占比的规律。Li Tian[4]对地下结构受内部爆炸时，覆土对结构的动态响应及冲击波超压传播的影响进行了研究。结果表明，覆土厚度对结构的动态响应有一定的影响；结构内部爆炸时冲击波的传播十分复杂，冲击波超压随与爆心比例距离的增大而减小。

在冲击波传播规律方面，仲倩等[5]、夏曼曼等[6]采用试验测试系统对炸药在空中爆炸时近区爆炸冲击波的传播规律进行了研究，提出了冲击波峰值超压与比例距离关系的修正经验公式。刘伟等[7]采用试验和数值模拟的手段对近地面TNT爆炸时比例距离小于4 m/kg1/3区域内冲击波的传播规律进行研究，将模拟结果与试验测试结果进行对比，验证了数值模拟算法及参数的准确性。辛春亮等[8]采用不同算法对TNT空中爆炸进行了冲击波超压计算，将数值模拟与经验公式计算所得超压值进行比较，得出了2种不同算法的优缺点。汪维等[9]采用数值模拟的方法对大当量TNT在空气中爆炸进行数值模拟，将计算结果与经验公式相比，得出了比例距离小于5 m/kg1/3时冲击波超压与冲击波到达时间随爆高的变化规律。

目前，学者们在结构受内部和外部爆炸时的动态响应方面研究较多，而在覆土库结构对冲击波传播影响方面研究较少。对于冲击波传播规律的研究，大部分学者侧重于炸药自由场爆炸情况下冲击波的传播，且研究范围较小，并未对炸药爆炸作用下覆土库结构外部较大范围内的冲击波传播规律进行研究。笔者采用非线性动力学有限元软件ANSYS/LS- DYNA，结合将覆土库结构破坏与冲击波传播先后模拟的新手段，对覆土库外部较大范围内爆炸冲击波传播规律进行研究。分别建立覆土库受炸药内部爆炸模型和冲击波在空气中传播的数值模型，提取炸药爆炸传出覆土库模型后不同方向单元内的压力时程，将其加载到冲击波在空气中传播的数值模型中，计算并提取不同测点处冲击波参数，得到覆土库结构对冲击波影响的传播规律。

1 数值模型

1.1 模型的建立

本模型是用于研究覆土库受1 t TNT内部爆炸作用下比例距离小于15 m/kg1/3范围内空气冲击波的传播规律。由于炸药当量较大，考虑空气冲击波传播范围较大，且涉及到覆土库的破坏过程，如果将覆土库的破坏与冲击波的传播在同一个有限元模型中进行模拟，模型网格量巨大，难以对该问题进行有效的数值模拟。因此提出了一种新的有限元模型建模方式，即将覆土库的破坏和冲击波的传播分别建立有限元模型，并先后进行模拟。覆土库模型与不同方向冲击波压力测试线的位置关系如图1所示，其中0°测线方向为覆土库前墙方向。

图1 数据测试线Fig.1 Data test line

覆土库的破坏模拟完成后，提取覆土库外0°、60°、90°、135°和180°方向单个空气单元内冲击波压力时程，将该压力时程作为冲击波传播模型中的等效爆炸荷载，加载到5个不同测线方向的冲击波传播模型中，对各个方向冲击波的传播过程分别进行计算。以0°测线方向冲击波传播计算为例，当覆土库的破坏模拟完成后，提取覆土库外部0°方向冲击波压力时程(见图2)。将0°方向冲击波传播模型起点处空气单元(见图5 BE处单元)设置压力输入属性，并在K文件中将所提取的压力时程数据点写入关键字* DEFINE _CURVE中，从而完成冲击波传播模型等效爆炸荷载的施加。

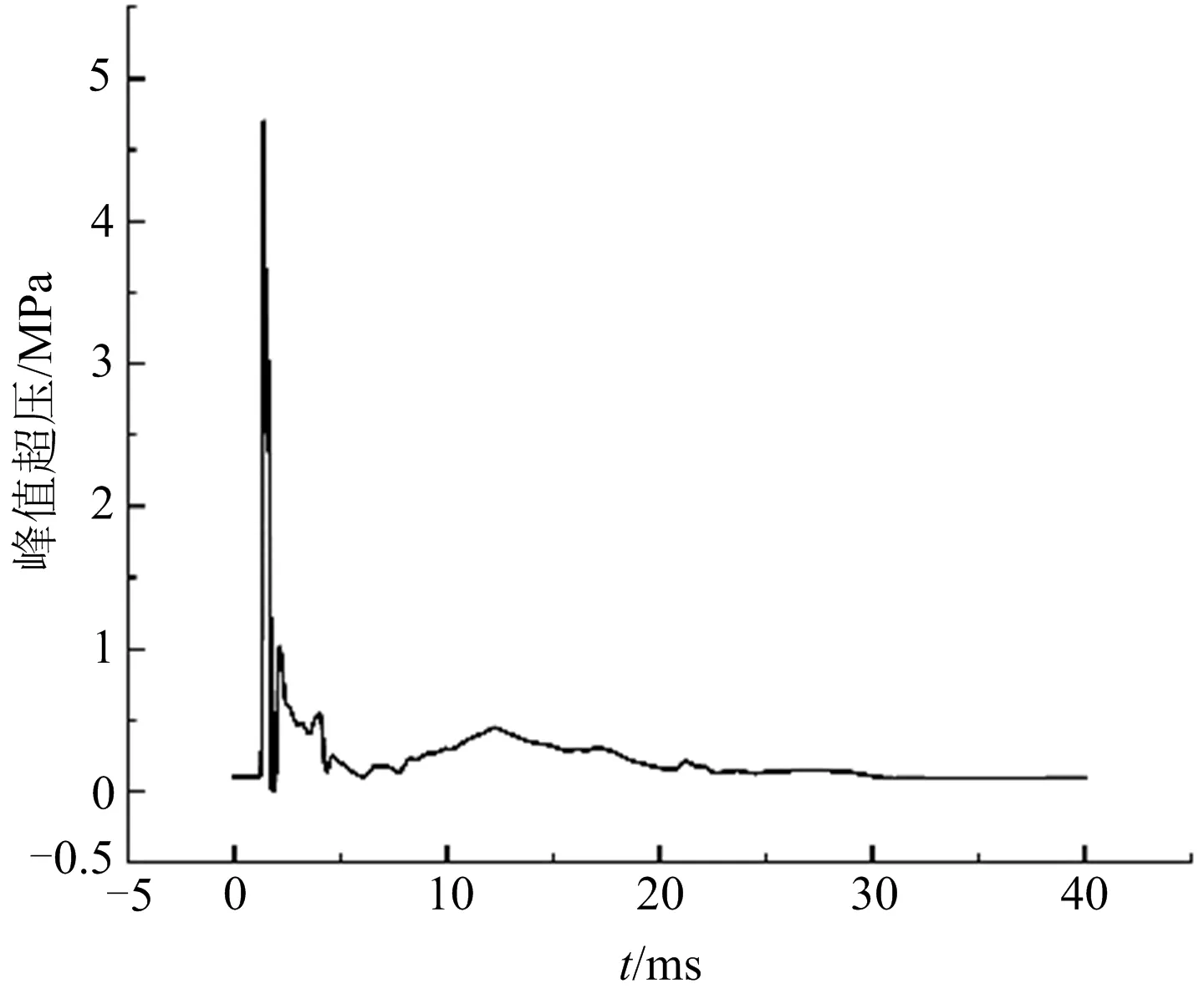
图2 0°方向等效爆炸荷载压力时程Fig.2 Time history of equivalent explosion load pressure in the 0° direction

对于覆土库受爆炸荷载破坏计算部分的数值模型，由于其具有对称性，为减少计算时间，只建立1/2有限元模型(见图3)。其中混凝土墙厚0.3 m。覆土库的主体结构是由波纹钢搭建而成，并在波纹钢拱顶部覆盖0.50 m厚的覆土。

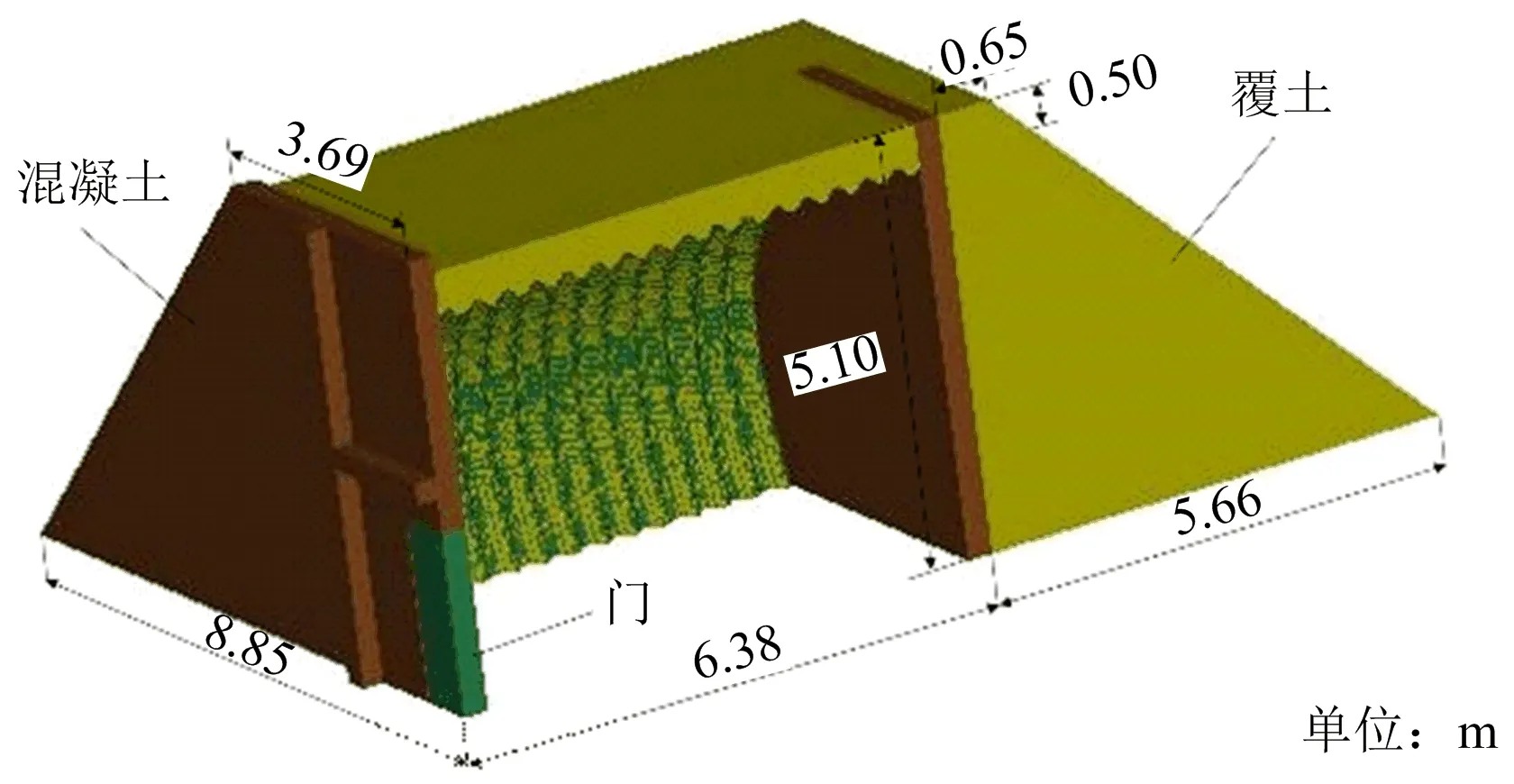
图3 覆土库模型Fig.3 ECM model

覆土库受炸药内部爆炸荷载作用下破坏过程的数值模拟采用流固耦合算法进行计算，需要建立流固耦合模型(见图4)。其中，钢筋与混凝土的耦合使用LS-DYNA中的关键字*CONSTRAINED_ LAGRANGE _IN_SOLID来实现。炸药放置于库体中心，其特征尺寸为0.85 m×0.85 m×0.425 m，空气模型的尺寸略大于覆土库结构模型特征尺寸。

图4 流固耦合模型Fig.4 Fluid-solid coupling model

对于空气冲击波传播计算部分的数值模型，需要考虑冲击波传出覆土库结构后在空气中的传播规律进行建模。文献[10]提到，冲击波在介质中的衰减规律，随距爆心比例距离的变化而变化。在比例距离小于5时，冲击波峰值超压在介质中呈二维衰减；在比例距离大于5 m/kg1/3时，冲击波峰值超压在介质中呈一维衰减。所以空气冲击波传播计算模型在比例距离小于5 m/kg1/3时为扇形形状；在比例距离大于5 m/kg1/3时，呈条形形状。

在炸药爆炸近区，测线方向覆土的有无会对冲击波传播计算模型近区的扇形形状产生影响。土体对爆炸冲击波具有很好的衰减作用，不同测线方向覆土的有无会对冲击波传出覆土库的时间产生影响。由于覆土库0°测线方向无覆土，此方向冲击波最先传出。在爆炸近区，冲击波不仅在竖直方向有压力衰减，而且在水平方向也存在压力衰减，故0°测线方向的冲击波传播计算模型在水平及竖直方向均采用扇形形状。覆土库结构在其他测线方向均有覆土对冲击波进行衰减，冲击波的传出时间基本一致。在爆炸近区，其他测线方向冲击波传播计算模型只在竖直方向采用扇形形状。

以0°测线方向冲击波传播模型中参数的计算原理为例，说明各测线方向冲击波传播模型参数的计算方法(见图5 ～ 图6)，其中O为爆心位置，A～L为冲击波传播模型各特征位置点编号。其中0°测线模型需考虑图5、图6中模型参数的计算，60°、90°、135°和180°测线方向只需要考虑图5中模型参数的计算。

图5 冲击波传播模型(侧视)Fig.5 The shock wave propagation model (Side view)

图6 冲击波传播模型(俯视)Fig.6 The shock wave propagation model (Top view)

如图5所示，将多次数值模拟所得冲击波峰值超压值与经验公式进行比较，得出在比例距离小于4.4 m/kg1/3时，冲击波呈二维衰减；在比例距离大于4.4 m/kg1/3时，冲击波呈一维衰减。故AF离爆心O的水平比例距离为4.4 m/kg1/3(即44 m)。BE右侧为覆土库破坏计算部分。覆土库破坏模型计算完成后，提取CD处一个单元内的冲击波压力时程加载到冲击波传播计算模型的空气域起点BE上。此计算方法需要保证提取冲击波压力时程的单元尺寸与加载冲击波压力时程的单元尺寸一致。在覆土库破坏模型中，空气的网格尺寸为10 cm，故冲击波传播计算模型BE处的网格尺寸也需要为10 cm。由于爆心高度为42.5 cm，取BE高50 cm，使BE处的高度正好为5个网格大小，以保证计算的精度。由BE高度和爆心的高度即可计算出扇形对应圆心角∠AOF的度数。取HJ为一个网格尺寸10 cm，同理可以计算出垂直于测线方向扇形的角度∠GOK的度数。

根据图5、图6冲击波传播模型参数计算方法所得各方向测线扇形角度如表1所示。

1.2 网格划分与边界条件

在数值模拟中，网格尺寸的大小对计算结果影响很大，需要选取合适的网格尺寸进行计算。覆土库破坏模型中取网格边长为10 cm。冲击波传播模型中取模型竖直方向网格尺寸为10 cm，网格尺寸随模型高度的增大而增大；在模型水平方向网格尺寸为固定值10 cm。将数值模拟结果与经验公式进行比较，证明了该网格尺寸计算的准确性。

数值模型的边界条件是数值计算过程中的重要步骤。对于流固耦合模型，混凝土与波纹钢底部采用全约束，取一半的对称面设置对称约束，其余表面不设置约束。空气和炸药模型在底部设置全约束，对称面设置对称约束，其余表面设置无反射边界。对于冲击波传播模型，在模型底部设置全约束，压力加载端不设置约束，模型远端设置无反射边界，其余表面设置对称约束。

1.3 材料参数

炸药选取TNT，采用MAT_HIGH_EXPLOSIVE _BURN材料模型，并利用JWL状态方程来实现爆炸荷载的施加[11],炸药材料参数如表2[12]所示。

表2 炸药材料参数

(1)

空气采用MAT_NULL材料模型和LINEAR _POLYNOMIAL状态方程来描述[11]：

p=C0+C1μ+C2μ2+C3μ3+(C4+C5μ+C6μ2)E

(2)

空气材料参数见表3[13]，其中ρ为材料密度，E0为初始内能。

表3 空气材料参数

土介质采用MAT_SOIL_AND_FOAM_FAILURE材料模型，其屈服函数为[11]

(3)

式中：a0、a1、a2为动力屈服常数；φ为土介质材料内摩擦角；sij为应力偏量；p为材料受到的压应力。

土介质材料参数如表4所示[13]。

表4 土介质材料参数

混凝土采用HJC材料模型，波纹钢和钢筋采用*MAT_PLASTIC_KINEMATIC材料模型，其材料参数如文献[14]所示。

2 模型验证

土体对于爆炸冲击波的衰减具有显著的作用。由于覆土库0°测线方向无覆土，炸药在覆土库内部爆炸后从该方向传出覆土库的冲击波峰值超压与同等药量炸药自由场爆炸冲击波峰值超压基本一致。提取覆土库0°测线方向不同比例距离处冲击波峰值超压，与Henrych、Mills和M.A.Sadovskyi经验公式计算所得冲击波峰值超压进行比较(见图7)。

图7 峰值超压模拟结果与经验公式计算结果Fig.7 The numerical and empirical formula results of peak overpressure

从图7可知，0°测线方向模拟冲击波峰值超压与3种经验公式在比例距离小于15 m/kg1/3时，冲击波峰值超压大小基本一致，冲击波峰值超压均呈指数型衰减趋势，验证了数值模型以及算法的正确性。

3 结果与讨论

通过对覆土库受内部爆炸作用下结构的破坏过程以及冲击波传播过程的模拟，对覆土库结构的破坏过程、冲击波峰值超压以及冲击波到达时间等数据进行分析，还原了覆土库受内部爆炸时的破坏过程，得出了冲击波的传播规律。

3.1 结构破坏过程

覆土库模型受炸药内部爆炸作用时的破坏过程如图8所示。

图8 覆土库破坏过程Fig.8 The destroys process of ECM

从图8可知，1.30 ms时，爆炸冲击波到达覆土库门以及后墙的位置，库门开始破坏；2.35 ms时，爆炸冲击波继续对覆土库结构进行冲击，库门及后墙破坏程度加剧，覆土库顶部由中心开始破坏；7.60 ms时，库体侧向及后部覆土库破坏，覆土库顶部完全破坏。

由于覆土库0°测线方向无土体覆盖，对爆炸冲击波的抵抗力最弱，故最先破坏。由于库体顶部覆土厚度相对于其他方向覆土厚度较小，对爆炸冲击波的抵抗能力也较弱。当爆炸冲击波作用于土体时，库体顶部覆土最先开始破坏，且完全破坏的时间也早于其他方向土体。

3.2 冲击波峰值超压

覆土库由于其结构的特殊性，受内部爆炸作用时，对冲击波的传播具有一定的导向性，不同测线方向冲击波的传播规律不同。为研究冲击波在不同测线方向上的传播规律，提取不同测线方向冲击波峰值超压值(见图9)进行比较。

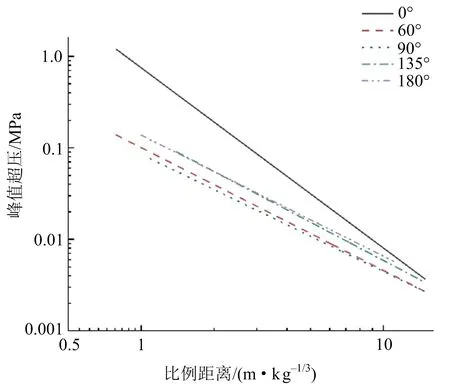
图9 不同测线方向峰值超压Fig.9 Peak overpressure in different directions

由图9可知，不同测线方向，同一测点的冲击波峰值超压不同。0°测线方向冲击波超压最大，因为0°测线方向无覆土，对爆炸冲击波的衰减能力最弱；135°和180°测线同一测点处峰值超压比60°和90°测线方向峰值超压略大，是因为135°和180°测线方向覆土库结构的破坏略早于60°和90°测线方向。不同方向冲击波峰值超压均呈指数型衰减规律，随着比例距离的增加，冲击波峰值超压趋于一致。测点距爆心比例距离越大，冲击波峰值超压受覆土库结构影响越小。

取不同比例距离处测点峰值超压拟合值进行比较(见表5)。当覆土库受内部爆炸作用时，含覆土测线方向的冲击波峰值超压明显低于0°测线方向冲击波峰值超压；当测点距爆心比例距离在1～15 m/kg1/3范围时，随比例距离的增加，冲击波峰值超压衰减率逐渐降低。分别提取60°、90°和135°、180°相同比例距离处冲击波峰值超压求和取平均值，计算各测线方向对冲击波峰值超压的衰减率。在60°和90°测线方向，随着测点比例距离的增加，冲击波峰值超压衰减率从87.63%降到26.39%；在135°和180°测线方向，随着测点比例距离的增加，冲击波峰值超压衰减率从81.19%降到1.39%。可以看出，60°和90°测线方向冲击波峰值超压最小，135°和180°测线方向冲击波峰值超压次之，0°测线方向冲击波峰值超压最大。在比例距离大于11 m/kg1/3时，0°测线峰值超压与135°和180°测线峰值超压相差低于20%；在比例距离为15 m/kg1/3时，0°测线峰值超压与60°和90°测线峰值超压相差25%。

表5 不同比例距离处峰值超压拟合值

3.3 冲击波到达时间

冲击波到达不同比例距离处的时间是描述冲击波传播规律的重要参数。不同测线方向冲击波到达时间的拟合曲线如图10所示。

图10 不同测线方向冲击波到达时间Fig.10 Arrival time of shock wave in different directions

由图10可以看出，不同测线方向冲击波到达各测点的时间呈线性增长。0°测线方向冲击波到达时间最早，135°和180°测线方向冲击波到达时间次之，60°和90°测线方向冲击波到达时间最晚。

4 结论

1)覆土库受内部炸药爆炸作用时，库门最先破坏，库顶次之，侧向覆土最后破坏。135°和180°测线方向的覆土破坏时间要早于60°和90°方向的覆土破坏时间。

2)覆土对冲击波峰值超压的影响，随测点比例距离的增大而减小。测点距爆心比例距离在1～15 m/kg1/3范围内时，随比例距离的增大，在60°和90°测线方向，冲击波峰值超压衰减率从87.63%降到26.39%；在135°和180°测线方向，冲击波峰值超压衰减率从81.19%降到1.39%。

3)冲击波到达时间随测点比例距离的增大，呈线性增大，0°测线方向冲击波到达各测点时间最早。