构造函数在高中数学解题中的应用分析

张 远

(江苏省扬州市邗江区公道中学 225119)

作为一种具有转化性质的数学思想，构造函数在高中数学教学中凭借自身的优势得到了广泛的应用.通过对构造函数的运用，能够将复杂、抽象的数学知识转变成学生熟悉、善于解决的问题形式，从而将数学问题由复杂化像简单化的方向转变.在具体应用过程中，要详细分析题目中给出的已知条件，并运用构造函数的方式，将向量、方程式、算数等问题进行构造，在此基础上，将得到的构造函数结合到题目给出的条件或者结论，得到对应的方程式.构造函数在高中阶段是一种具有多元化特点的解题工具，因此加大培养学生使用构造函数的力度，能够在一定程度上提升学生灵活运用数学知识的能力.

一、构造函数法的基本内涵

根据对高中数学解题方法展开的大量实际调查研究能够知道，在解决高中数学问题的过程中，运用构造函数的思维和方法，能够在很大程度上降低数学题的难度.对数学问题的题干进行梳理、对内容进行分析，结合新的函数、方法、图形等手段，将原本抽象、复杂、模糊的数学问题变得具体、简单、清晰，使学生通过解决多个简单的数学问题将一个复杂的数学问题有效解决，这就是构造函数发挥作用的具体流程.对于构造函数解题方式而言，是一种具有较高的创造性和灵活性的函数形式，通过解答问题产生的一种有效的解题模式.通过对原题进行仔细的分析，构造出对应的函数关系，并且结合题目对构造出的函数进行严格的分析和整理，从而得到正确答案，保证学生解决数学问题的高效性.在利用构造函数方法解决数学问题的过程中需要注意，构造出的数学函数必须具备以下几个特点，第一，函数的建立必须能够与原题之间保持有效的联系.第二，必须保证构建出的函数具有的解题难度比原有解决方法的难度小.第三，构造出的函数在周期性、奇偶性、单调性、值域等方面必须与题目相符，这样能够有效杜绝构造函数错误的情况发生.第四，要结合题目的内容进行对应函数的构造.除此之外，在进行函数构造的过程中还需要注意，要对命题的条件、结论、特点等进行分析，通过提取出其中的逻辑、构想等，依照题目条件进行重新组合，从而得出解题所需要的构造函数.对函数进行观察和分析，从而分析条件与结论的联系.

二、构造函数法之高次函数构造

在利用构造函数解决高次函数问题时，可以对高次函数的题目进行分析，通过对小问题的逐个解决，将高次函数问题正确解答.比如，在解答范围求解相关问题的过程中，可以通过构建高次函数的方式，将题目给出的已知条件进行有效的利用.

问题如果当sin3θ-cos3θ>cos5θ-sin5θ，θ∈(0,2π)的不等式关系存在时，题目中角θ的范围值是多少？

解根据题目sin3θ-cos3θ>cos5θ-sin5θ，θ∈(0,2π)能够知道sin3θ+sin5θ>cos3θ+cos5θ.此时，假设f(x)=x3+x5，不等式能够成立，并且函数f(x)=x3+x5在(-，+)范围中，属于增函数，那么，能够得到不等式f(sinθ)>f(cosθ)之间的关系，因此，根据上述分析能够确定sinθ>cosθ.与此同时，由于θ∈(0,2π)，所以能够得到结果

通过对以上问题的解决能够看出，运用的就是高次函数f(x)=x3+x5的构造方式，在此基础上，结合函数具有的单调性特点，对不等式进行转换，这样，就能将角θ的取值范围准确地求出.

三、函数构造法之指数函数构造

在运用构造指数函数解决高中数学问题的过程中，能够将复杂的数学问题分解成简单的问题，使学生在解决简单数学问题的同时，将复杂的数学问题有效解决.

问题已知一个三角形的三条边分别为a、b、c，并且它们之间存在一定的关系a2+b2=c2.现设n表示某个正整数，并且n>2，那么，cn>an+bn的不等式关系是否成立.

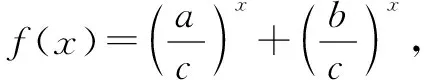
四、函数构造法之一次函数构造

在运用一次函数构造的方式解决数学问题的过程中能够发现，构造函数的使用能够将数学问题的难度有效降低，提升学生解决数学问题的信心.

问题如果不等式2x-1>m(x2-1)在|m|≤2|的条件下成立，求未知数x的取值范围.

解在解决这道数学问题时，要先将题目中给出的不等式条件进行转化，使之变成(x2-1)m-(2x-1)<0，然后对该不等式进行一次函数的构造，使之以(x2-1)m-(2x-1)<0(其中|m|≤2)的形式呈现出来.在此基础上，按照该不等式的一次函数实际图象具有的基本性质进行计算，从而能够得到的不等式关系f(2)<0,f(-2)<0，就能得到具体x的取值范围.

五、函数构造法之二次函数构造

在解决下列数学问题时，将构造函数的方式结合其中，能够将问题的难度有效降低，使学生解决数学问题的兴趣和能力有效提高.

问题如果a,b,c∈R，并且a+b+c=1,，a2+b2+c2=1，那么a的取值范围是多少？

解在解决这个数学问题时，要对题目中给出的已知条件进行详细的分析，然后将关系式a+b+c=1转变成b+c=1-a，将关系式a2+b2+c2=1转变成b2+c2=1-a2.在此基础上进行二次函数的构造，得到函数f(x)=2x2-2(b+c)x+b2+c2=(x-b)2+(x-c)2≥0，从而得到关系式Δ=4(b+c)2-8(b2+c2)≤0，在此基础上，对该不等式进行更深一步的化简，得到4(1-a)2-8(1-a2)≤0，最终，通过计算得到a的取值范围.

针对上述类型的数学问题而言，在解决的过程中的关键点是将b+c和b2+c2看作是一个整体，以此为基础，通过利用二次函数构造的方式对原等式进行简化，得到原等式的不等式关系，从而得到正确的结论.

综上所述，根据以上针对构造函数在高中数学解题中的应用，展开的系统性分析，我们能够更加深入地了解构造函数在数学解题中的重要性.作为高中阶段数学知识重要的组成部分之一，函数本身占居了重要的地位，而在解决数学问题中运用构造函数的方式，也是一种有效的解题思路，不但能够使学生的解题思维水平提升并扩展，还能将学生灵活运用数学知识的能力有效提升.因此，加强对构造函数的重视力度，掌握运用构造函数的技巧，有效提升学生的综合数学素养.