面心和体心立方晶体中映像规则判断始滑移系的原理
杨晓冬, 杨静
(1. 华侨大学 材料科学与工程学院, 福建 厦门 361021; 2. 厦门大学 化学化工学院, 福建 厦门 361005)
单晶体系是研究材料塑性变形的最简单体系,诸多塑性变形理论均是在单晶体系中提出并发展的.Schmid等[1-2]对金属晶体的塑性变形进行总结,并提出著名的Schmid定律.Schmid定律可以表述为对同种材料但取向不同的单晶试样棒进行拉伸,滑移总发生在特定的平面和方向上,且在滑移启动时,分解到滑移发生的平面和方向上的临界分切应力为定值.滑移面和滑移方向的空间组合称为滑移系,最先开动滑移的系统称为始滑移系.显然,在所有的滑移系中,始滑移系的分切应力最大.在晶体上施加任意载荷时,始滑移系的判断方法通常有两种:一是按照Schmid定律计算载荷在所有滑移系的分切应力,比较并确定数值最大的滑移系为始滑移系[3-6];二是通过映像规则进行判断[3,7],映像规则也称为Diehl规则[8-11],应用于常见的面心立方晶体和体心立方晶体中.
映像规则是基于Schmid定律判断始滑移系的方法总结而来的规律[3].在现有的资料中,仅有范群成等[12]根据“始滑移系的φ和λ同时接近中等值”定性地论述映像规则的原理,Kelly等[10]通过计算面心立方晶体和体心立方晶体的12组滑移系的Schmid因子,证明了映像规则的科学性.基于此,本文提出一种简单、直接、易于理解且严谨的证明方法,利用标准投影图中力轴与滑移系的几何关系解释映像规则,并结合标准投影图从数学角度证明映像规则.
1 映像规则
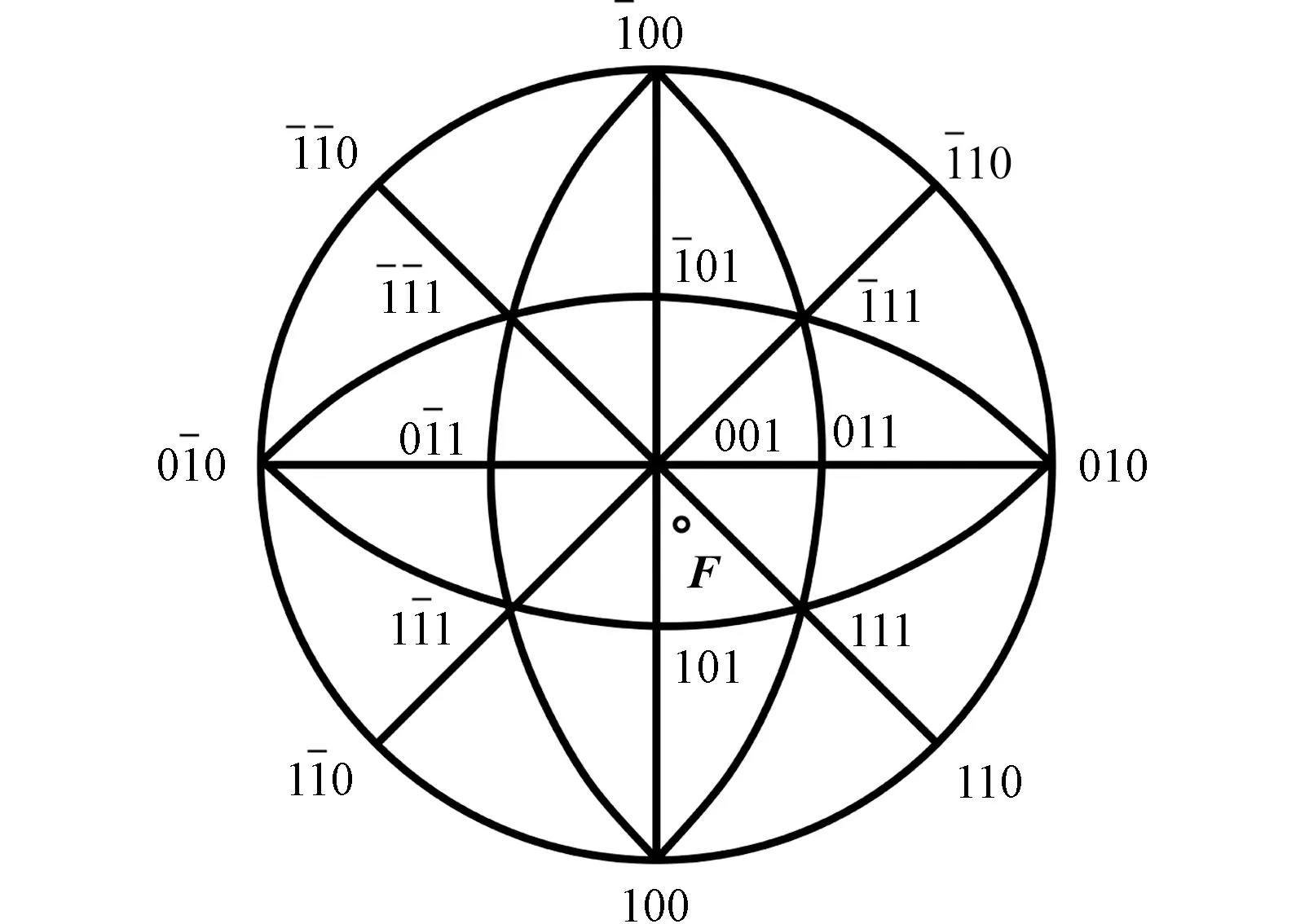
图1 立方晶体(001)的标准投影图Fig.1 (001) standard stereographic projection of cubic crystal
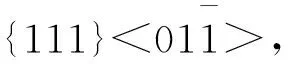
2 图解映像规则
为了更直观地在标准投影图上展示力轴与滑移系的关系,在单晶试样棒的单向拉伸立体图上分解力轴与滑移系.图2示意了力轴(F)、滑移面(法线N)和滑移方向T在单晶试样棒上的几何关系.通过简单的运算,F分解到T方向上的分切应力τ[3-4,15]为
(1)
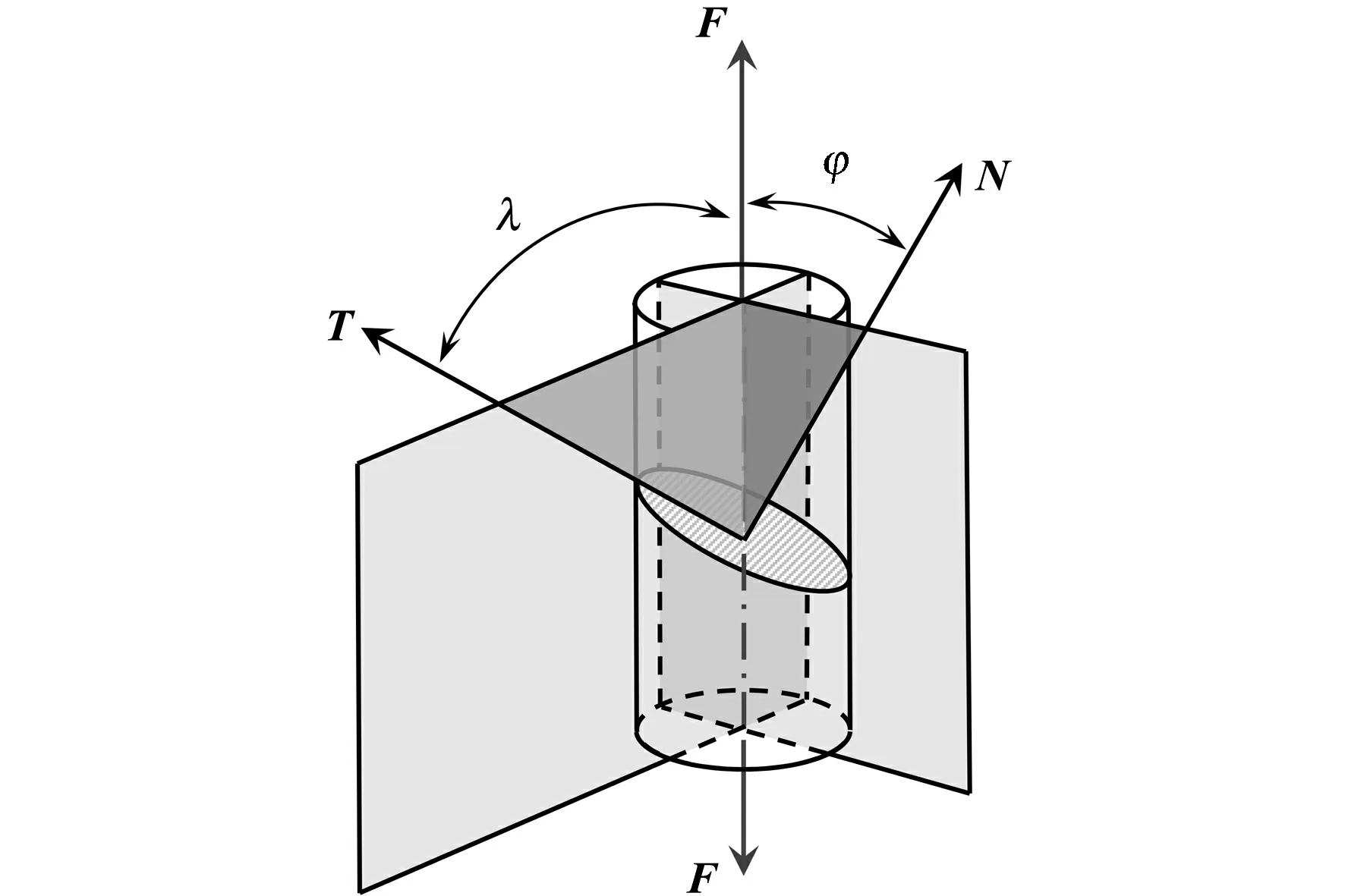
图2 单晶棒的单向拉伸示意图Fig.2 Schematic of uniaxial tension of single crystal rod
式(1)中:A0为试样棒的截面面积;φ为力轴F与滑移面法线N的夹角;λ为F与滑移方向T的夹角;cosφ·cosλ为Schmid因子,用m表示,其数值越大,则分切应力越大.
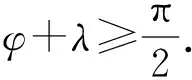
为了便于理解,下文将统一称平面N×T为滑移系平面.
由图2可知以下边界条件,即
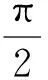
,
(2)
(3)
(4)
Schmid因子可通过三角函数变换为
(5)
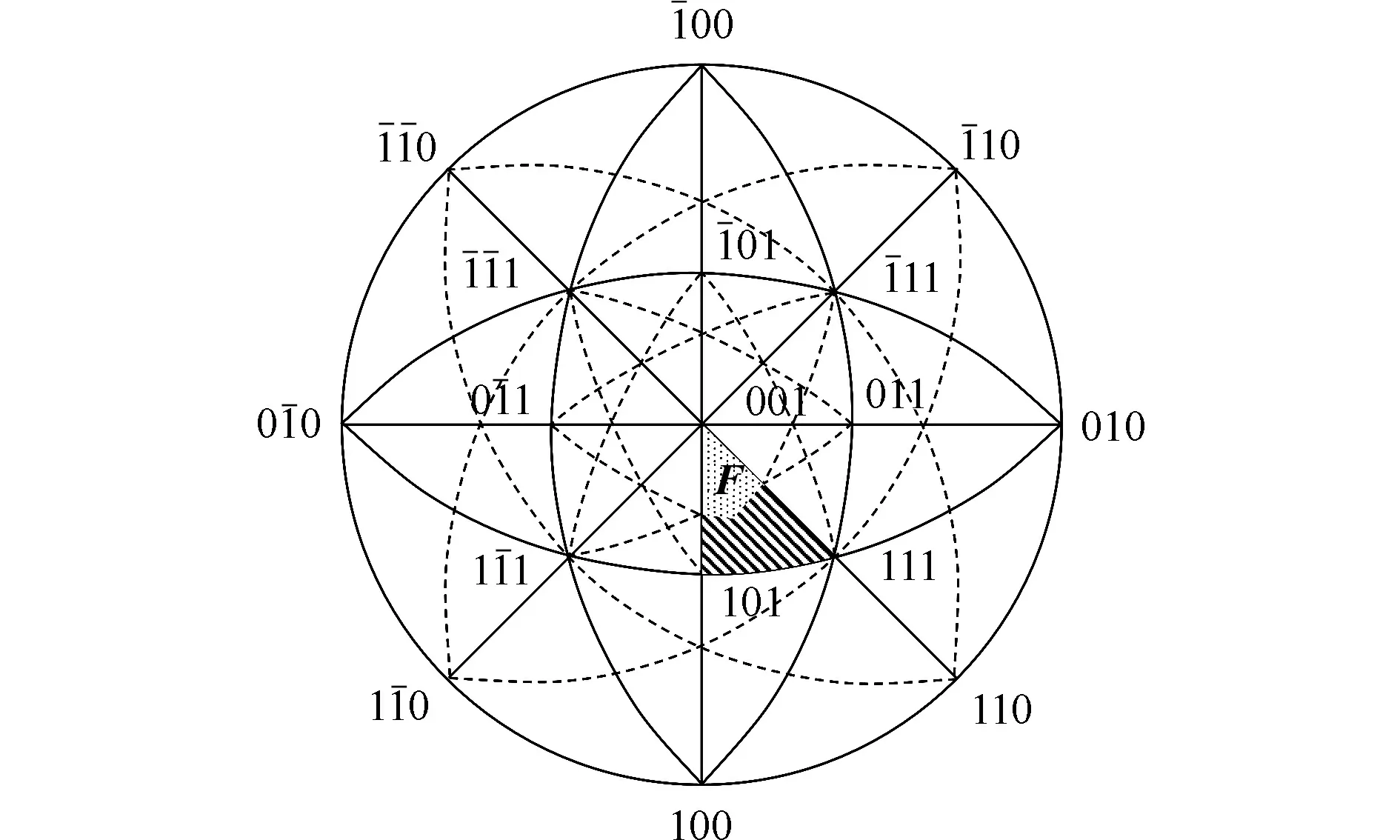
图3 (001)标准投影图中面心立方体的等价滑移系Fig.3 Physically distinct glide systems of face-centered cubic crystal in (001) stereographic projection

事实上,取向三角形中的部分区域并不能直观地比较这3个滑移系平面的Schmid因子相对大小,究其原因主要有以下2点.
1) 在标准投影图中,不能便捷、精确地测量夹角,只能通过曲线的长度定性地估算夹角[16],但这是不准确的.例如,[111]与[001],[010]的夹角相同,但显然两条线长度并不相同.

由此可知,通过“力轴靠近滑移系平面”和“夹角φ,λ接近”在标准投影图上定性解释映像规则有所局限,使用时需考虑其适用性.然而,此方法可直观地呈现出映像规则的本质是结合标准投影图中的夹角φ,λ判断Schmid因子大小,便于初学者快速理解映像规则.因此,需进一步通过数学计算求出Schmid因子前三强中的最大者,从而确定始滑移系,以证明映像规则.
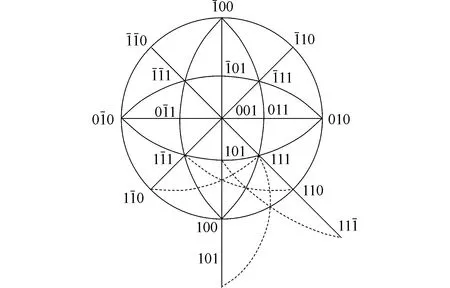
图4 外围取向三角形的滑移系组合Fig.4 Glide systems of outer unit triangle
需要说明的是,[001]周围的8个取向三角形均示意出3组滑移系(图3),但在外围的16个取向三角形中,仅示意出一组或两组滑移系,即只有一条或两条虚线切过.事实上,根据立方晶体的周期性和对称性,外围16个取向三角形中均有3个滑移系平面切过.图4补充了外围取向三角形的滑移系平面.为了简洁示意,以100-111-101,100-110-111取向三角形为例,对外围取向三角形的滑移系平面进行补充.由图4可知:当力轴位于外围取向三角形时,仍可根据“力轴靠近滑移系平面”和“夹角φ,λ接近”快速筛选出3个最有可能的滑移系.
3 映像规则的数学证明
Schmid因子可通过矢量运算表达为
(6)
假设F为[uvw],N为[h1k1l1],T为[h2k2l2],则式(6)可展开为
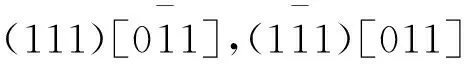
(7)
(8)
(9)
力轴F在取向三角形101-111-001的位置可分成以下3种情况:1) 位于三角形内;2) 位于3条边;3) 位于顶点.为了便于确认边界条件和限制条件,将矢量F放回立方晶体的取向胞中.立方晶体取向胞,如图5所示.图5中:阴影区域为取向三角形101-111-001.矢量F可描述为起点位于O,经过粉色区域的矢量.将矢量F和阴影区域的交点投影至取向胞中的三维坐标轴上,便可得到边界条件.
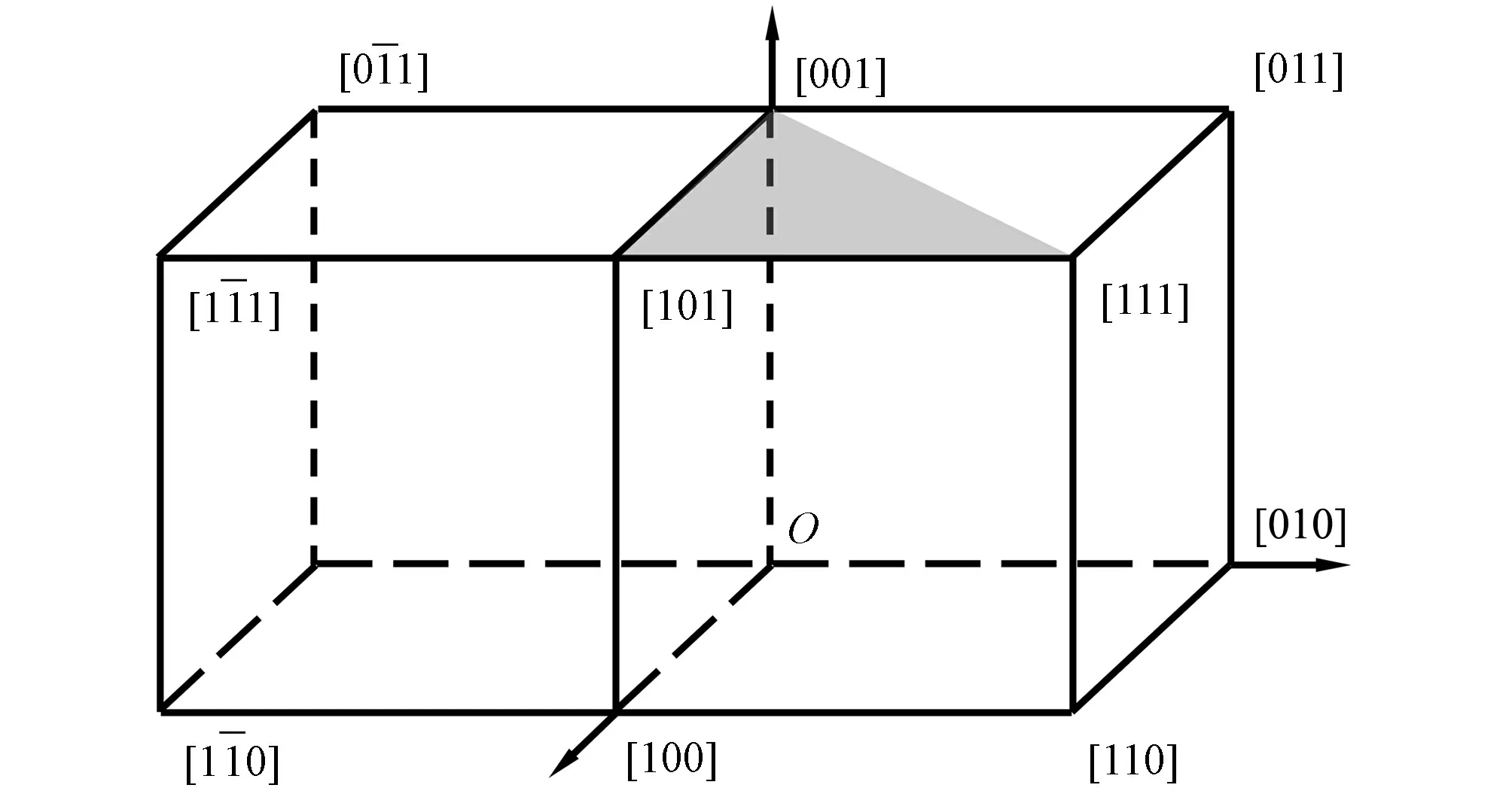
图5 立方晶体取向胞Fig.5 Unit cell of cubic crystal
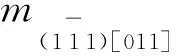
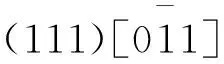
(10)
(11)
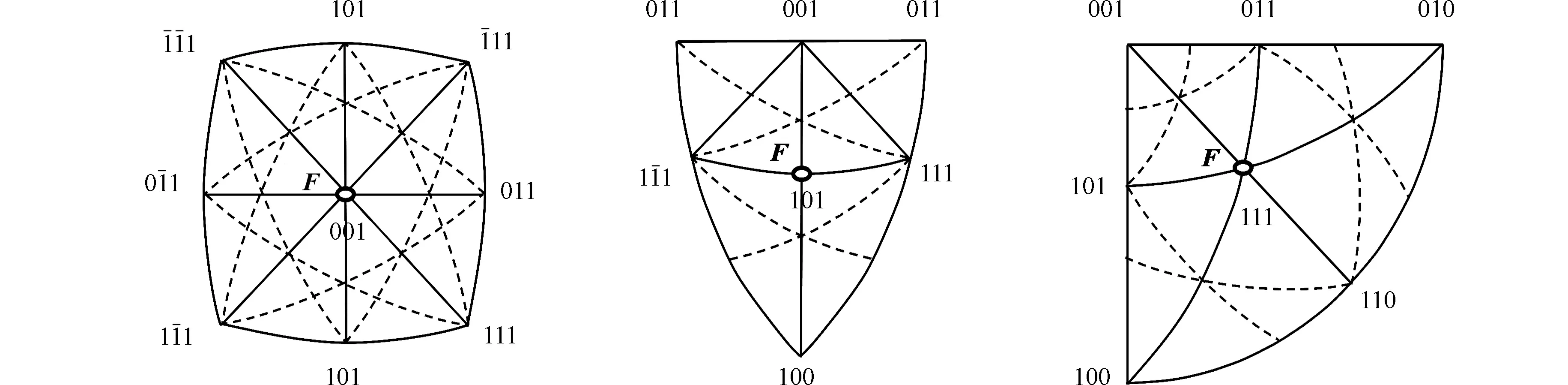
同理,当F位于001-101边时,v=0,0 (12) (13) 当F位于101-111边时,v (14) (15) (16) 当力轴处于顶点处时,需考虑共顶点的所有三角形的滑移系.因为此时力轴相对于这些共顶点的三角形是等同的.例如,当力轴位于[001]时,需同时考虑共001顶点的8个取向三角形.如上文所述,每个取向三角形均有3个可能的滑移系.根据标准投影图可以定性地筛选出切过每个共顶点三角形的3个滑移系.力轴位于顶点时的始滑移系,如图6所示. (a) [001] (b) [101] (c) [111]图6 力轴位于顶点时的始滑移系Fig.6 Initial glide systems when tension force located at junctions 当力轴位于[001]时,由图6(a)可知:筛选出的8个滑移系均关于力轴[001]对称;8个滑移系的Schmid因子相等且最大,都是始滑移系.不难验证,这8个始滑移系与根据映像规则判断出的始滑移系相同. 同理,当力轴位于[111]时,无需考察经过[111]的滑移系.由图6(c)可知:定性筛选出的滑移系有4个,且关于[111]对称,均为始滑移系,仍然符合映像规则. 综上论述,在取向三角形101-111-001的任何位置均符合映像规则.由于立方晶体的高度对称性和周期性,当力轴位于其他取向三角形,即立方晶体标准投影图的所有位置,均可以运用映像规则判断始滑移系. 将Schmid因子变换为关于φ+λ和φ-λ的余弦函数(式5),并结合标准投影图的力轴位置可知,当“力轴靠近滑移系平面”和“夹角φ,λ接近”时,Schmid因子最大,可以此确定始滑移系.此论述对映像规则进行形象的解释,易于理解,十分适合初学者,也可供讲授者参考.在此基础上,进一步结合矢量运算,从数学角度证明力轴取向与始滑移系的关系符合映像规则.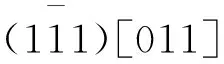
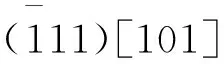
4 结束语

