IRR柱承台局部压应力分布及其计算方法
许一鹏, 刘阳,2, 林茂彬, 郭子雄,2
(1. 华侨大学 土木工程学院, 福建 厦门 361021;2. 华侨大学 福建省结构工程与防灾重点实验室, 福建 厦门 361021)
随着社会经济的不断发展和结构工程领域研究的不断深入,结构在遭遇罕见地震后的“性能可恢复能力”已经得到全世界结构工程专家的重视.工程结构抗震理念已经从抗倒塌逐渐向结构功能或性能的可恢复转变,成为近年来发展的重要趋势[1-2].为实现框架结构的性能可恢复,国内外学者开展了一系列研究.如Oh等[3]、Shen等[4]、郭子雄等[5]、刘阳等[6]、邵铁锋等[7]和Calado等[8]围绕钢框架和混合框架结构中的钢梁和混合节点等部位开展了相关研究.为了实现框架结构体系的震后性能恢复,不可避免地要考虑底层柱脚塑性铰区的替换问题,而国内外对这方面的研究还相对不足.
在前期研究的基础上,本课题组[9-12]提出多种柱脚震损原位替换的构造.其中,带开缝钢板阻尼器的新型性能可恢复摇摆柱(innovative resilience rocking column,简称IRR柱)因构造简单、施工和修复方便,是一种良好的技术选择.前期研究表明,按照“强柱弱阻尼器”的原则设计得到的IRR柱具有优越的抗震性能和良好的性能可恢复能力[9].同时,在水平荷载作用下,钢柱发生摇摆,柱底承台处于局部受压状态.为了保证承台不发生局压破坏,本文采用有限元方法,对不同参数的IRR柱柱底承台上表面局压应力分布进行研究.
1 新型可恢复摇摆柱有限元模型
新型性能可恢复摇摆柱与传统框架结构的对比,如图1所示.传统框架结构会在柱根位置出现塑性铰,导致结构发生破坏,而IRR柱的摇摆机制能很好地避免该缺点.
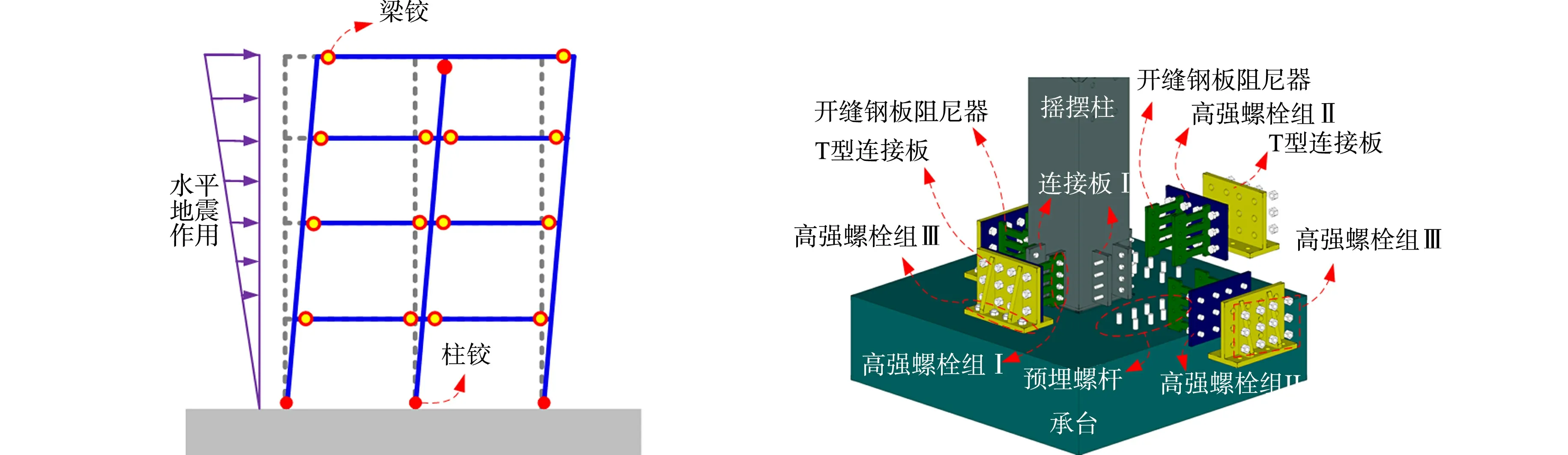
(a) 传统框架结构 (b) IRR柱 图1 新型性能可恢复摇摆柱与传统框架结构的对比Fig.1 Comparison of IRR column and traditional frame structure

图2 IRR柱的变形示意图 图3 IRR柱的详细尺寸(单位:mm)Fig.2 Deformation schematic diagram of IRR column Fig.3 Detailed measurement of IRR column (unti: mm)
1.1 单元类型和材料本构
网格划分的单元类型采用八节点六面体缩减积分格式(C3D8R)的三维实体单元.加载过程中,局压区域外的承台和柱身保持弹性状态,因此,网格划分较稀疏,网格尺寸为50~200 mm,连接板和T型连接件网格尺寸均为20 mm.螺栓不仅承担了预紧力,加载过程中还可能存在法向力和切向力,受力状态复杂,因此,网格划分最密,网格尺寸为8 mm.柱身下承台的局部受压是研究的重点,因此,对局压部分的网格进行局部加密,最小网格尺寸为10 mm.承台局部网格划分,如图5所示.

图4 IRR柱有限元模型 图5 承台局部网格划分 Fig.4 Finite element model for IRR columns Fig.5 Local meshing of foundation
柱身、连接板和T型连接件均采用Q345钢,屈服强度标准值取345 MPa;开缝钢板阻尼器采用Q235钢,屈服强度标准值取235 MPa;钢材本构均采用理想弹塑性模型.高强螺栓采用10.9级,屈服强度取900 MPa,抗拉强度取1 000 MPa,采用双折线弹塑性应力-应变曲线.所有钢材泊松比取ν=0.3.
1.2 接触界面模拟
T型连接件、开缝钢板阻尼器和连接板之间的界面,以及承台和柱底的界面均由切线方向的库伦摩擦接触及法线方向的硬接触组成.库伦摩擦接触公式选用“罚函数(penalty)”,摩擦系数取0.3[13],法向行为采用“硬接触(hard contact)”;接触单元采用“表面与表面(surface-to-surface)”的接触方式.螺栓与螺栓孔之间由于相对滑移很小,其界面仅考虑硬接触;螺栓与T型连接件、开缝钢板阻尼器和连接板之间的界面采用摩擦接触.T型连接件与承台、连接板与柱身之间的焊接等均采用“绑定(tie)”进行模拟.
图6 水平荷载加载制度Fig.6 Horizontal loading protocol
1.3 加载方式和边界条件
在有限元分析中,对拟静力试验进行验证.模型有3个分析步骤:1) 通过“螺栓荷载(bolt load)”施加所有螺栓的预紧力;2) 采用“集中力(concentrated force)”在试件上方施加竖向荷载,根据轴压比的参数设置竖向力的大小;3) 施加往复位移作用,水平荷载加载制度[14],如图6所示.图6中:N为试件加载的循环次数;θ为位移角.3个分析步骤依次传递相互作用.承台底部采用固定端,在初始分析步骤设置.
2 模型的验证
2.1 模型合理性分析
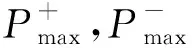
由图7(a)可知:采用精细化有限元模型计算所得荷载-位移曲线与试验结果吻合良好.有限元计算结果可以很好地模拟IRR柱摇摆过程中引起的滞回曲线捏拢现象.高强螺栓从“摩擦型”到“承压型”的转变,导致加载刚度的变化也能很好的体现.由图7(b)中精细化模型和试验所得荷载-位移骨架曲线的对比可以清晰地看到二者之间的差异.由此可知,精细化有限元模型可以比较合理地反应IRR柱的受力特点,并相对准确地计算其承载力、刚度和耗能等指标.

(a) 精细化模型计算滞回曲线 (b) 骨架曲线对比 图7 有限元模型计算试件S16-5.5-0.1滞回曲线对比Fig.7 Comparison of finite element and tested hysteretic curves for S16-5.5-0.1
考虑到承台局压应力分布的最不利状态仅与试件最大承载力相对应,模型计算得到的试件最大承载力状态下承台法向方向的局部压应力(σN)分布曲线,如图8所示.图8中:水平坐标X表示承台与柱底接触部分从抬起侧到局压侧的相对距离,方向定义详见图8插图.由图8可知:水平荷载作用下,柱底承台局部压应力主要分布在靠近转动点很小的范围内,受压区宽度约为20~30 mm.
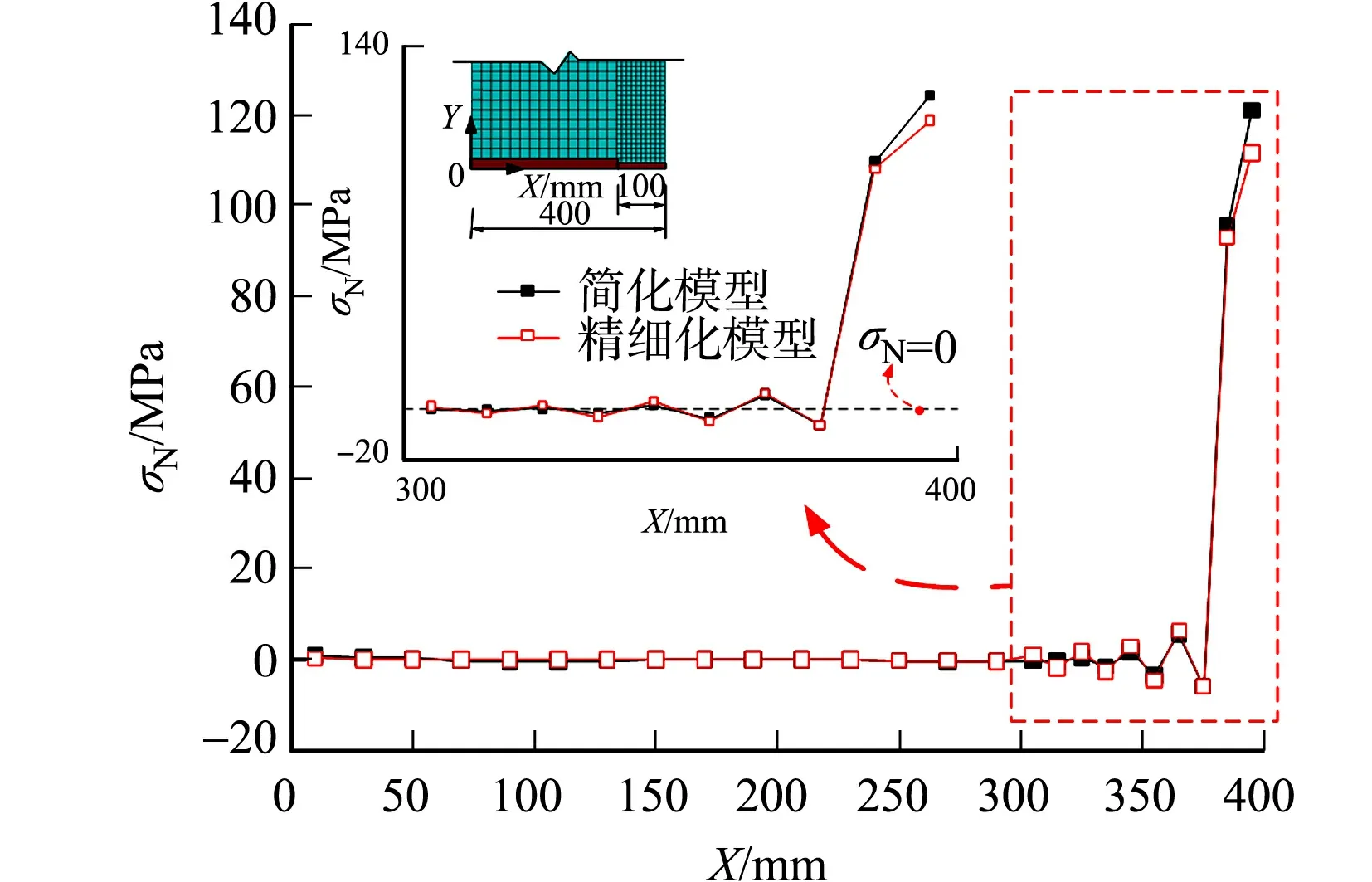
图8 有限元模型承台法向局部压应力分布曲线Fig.8 Distribution curve of local bearing stress in vertical direction of foundation of finite element model
2.2 局部压应力分布
以试件S16-5.5-0.1的有限元模型计算结果为例进行说明.柱底在承台接触投影面积范围内,分别提取3个平行于加载方向的纵剖面1-1,2-2和3-3(图5),截面间隔为100 mm.在水平荷载达到峰值状态下,3个不同截面位置的承台局部压应力分布曲线,如图9(a)所示.在不同位移角下,1-1截面处的承台局部压应力分布曲线,如图9(b)所示.
由图9(a)可知:在0~300 mm范围内,由于柱脚抬起,承台的压应力基本接近于0,水平位置越接近400 mm处,压应力就越大.柱身是箱型截面,由于剪力滞后效应,承台中心位置所受的压应力相对较小,靠箱型外边缘的1-1截面压应力最大.后续分析均以1-1截面对应的局部压应力数据进行讨论.

(a) 不同截面压应力 (b) 不同位移角幅值图9 承台局部压应力分布曲线Fig.9 Distribution curves of local bearing stress of foundation
由图9(b)可知:随着加载位移角的增大,柱底承台压应力的最大值也相应增大,1/20位移角下,柱底边缘处局部压应力达到最大值,约为120 MPa.可见,最不利状态下的承台局部压应力远远超过承台混凝土强度,应该做好防止局压破坏的构造处理.考虑到局部压应力的分布面积较小,且承台混凝土局压强度高于其抗压强度,建议在柱底承台表面局部设置一层厚度为4~6 mm的钢板.根据试验结果[15]可知,该构造在轴压比n≤0.2时,承台出现局压破坏.由图9(b)还可知:当位移角小于1/35时,局压应力基本呈线性分布;当位移角大于1/25后,局压应力近似为抛物线分布.该分布形式可为后文理论计算公式的提出作参考.
3 参数分析
为了研究不同设计参数对承台最大局压应力的影响规律,并对最大局压应力计算公式的提出提供数据参考,采用精细化有限元模型进行参数分析.
3.1 轴压比
柱身承担的轴力大小是影响试件柱底承台压应力的主要因素.参照钢筋混凝土柱轴压比的定义,计算IRR柱的设计轴压比n,即
n=F/(fyA).
(1)
式(1)中:F为IRR柱承担的轴力设计值;fy为钢材屈服强度设计值,取fy=fyk/1.1,fyk为钢材屈服强度试验值;A为IRR柱横截面的面积.
当不同参数的试件水平位移达到1/20位移角时,提取其1-1截面处的压应力最大值,得到轴压比对承台局部压应力最大值的影响,如图10所示.图10中:σmax为局部压应力最大值;d为阻尼器厚度.由图10可知:局部压应力最大值随轴压比的增加而增加,增加速度随着轴压比的增大而减小,局部压应力最大值已超过300 MPa,可见混凝土承台已经不能满足局部承压的需求,必须进行构造加强.
由图10还可知:当试件轴压比从0.1增加到0.4时,阻尼板厚度为8 mm的试件的承台局部压应力最大值由原先的101.1 MPa变为276.0 MPa,增加了172.9%;阻尼板厚度为16 mm的试件的承台局部压应力最大值由原先的120.8 MPa变为293.4 MPa,增加了142.9%.
3.2 阻尼器厚度
不同阻尼器厚度对承台局部压应力最大值的影响,如图11所示.由图11可知:在相同的轴压比下,随着阻尼器厚度的增加,承台最大压应力值基本呈线性增大,但增加幅度较小;当轴压比为0.2,0.3时,阻尼器厚度从8 mm增加到20 mm,承台最大局部压应力分别增加了14.3%和41.2%,其余厚度的阻尼器对应的试件承台最大局部压应力的增长范围均在该区间内.
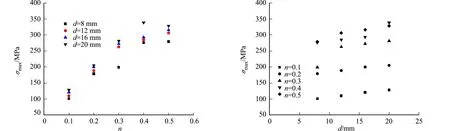
图10 轴压比对承台局部压应力最大值的影响 图11 阻尼器厚度对承台局部压应力最大值的影响 Fig.10 Influence of axial compression ratio on Fig.11 Influence of damper thickness on maximummaximum value of local bearing stress of foundation value of local bearing stress of foundation
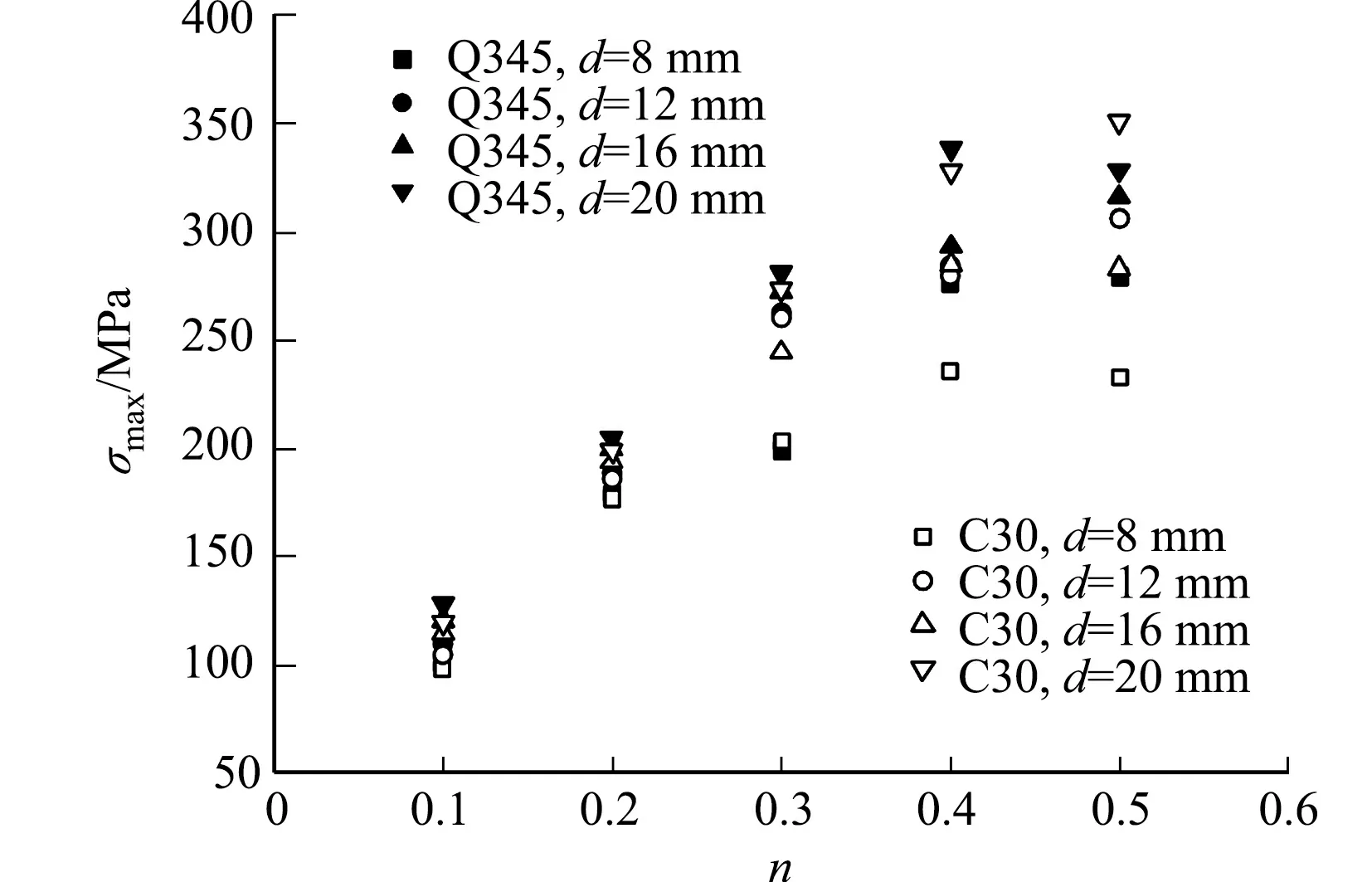
图12 材料弹性模量对承台局部压应力最大值的影响Fig.12 Influence of material elastic modulus on maximum value of local bearing stress of foundation
3.3 承台材料的弹性模量
为防止承台的局压破坏,工程中一般根据最大局压应力的大小,采取不同的承台构造.局压应力较小时,可以直接采用素混凝土;局压应力较大时,可在混凝土中局部设置多层钢筋网片,或者设置钢垫板.在有限元分析时,承台简化成单一弹性材料,不同的工程构造反应在模型中即为弹性模量的差异,而不同的弹性模量在相同的局压力下,会导致承台上表面局压面积的不同,进而导致最大局部压应力的不同.选取C30混凝土和Q345钢材的弹性模量作为上、下限进行计算并对比.材料弹性模量对承台局部压应力最大值的影响,如图12所示.
由图12可知:尽管承台定义的弹模数值差异较大,所提取的最大压应力差异并不显著,个别数值存在较大的跳动,但均不超过15%的差值范围.
轴压比为0.5的试件在位移角超过3/100时,柱角处单元的塑性应变累积大于0,即柱子开始发生塑性损伤.因此,在提取的计算公式中,轴压比为0.5的试件不纳入考虑范围.
4 最大局部压应力的计算公式
4.1 局部压力
按照“强柱弱阻尼器”原则设计的IRR柱在最大承载力状态下,塑性变形集中在钢板阻尼器的水平条带板上,条带板处于弯曲和拉压复合受力状态.其他部件均处于弹性受力阶段,与条带板充分发展的塑性变形相比,其弹性变形可以忽略.假设水平条带板的弯曲和拉压变形可以单独考虑,并将其简化为一维杆件,弯曲变形集中于杆件两端的0长度弯曲塑性铰上,拉压变形均匀分布于一维杆件上,其他部位均等效为刚体,建立的IRR柱简化受力分析模型,如图13所示.图13中:a为钢柱柱宽;b为柱身连接板宽度;L为条带板长度;H为钢柱高度;ai为承台上表面到水平条带板形心距离,i为条带板编号,i=1,2,…,8;δi是条带板的拉伸变形;α为柱底面与承台夹角;δ为柱脚抬起高度;xi和yi分别为第i条条带板与柱身相连一侧在x和y方向上的变形.
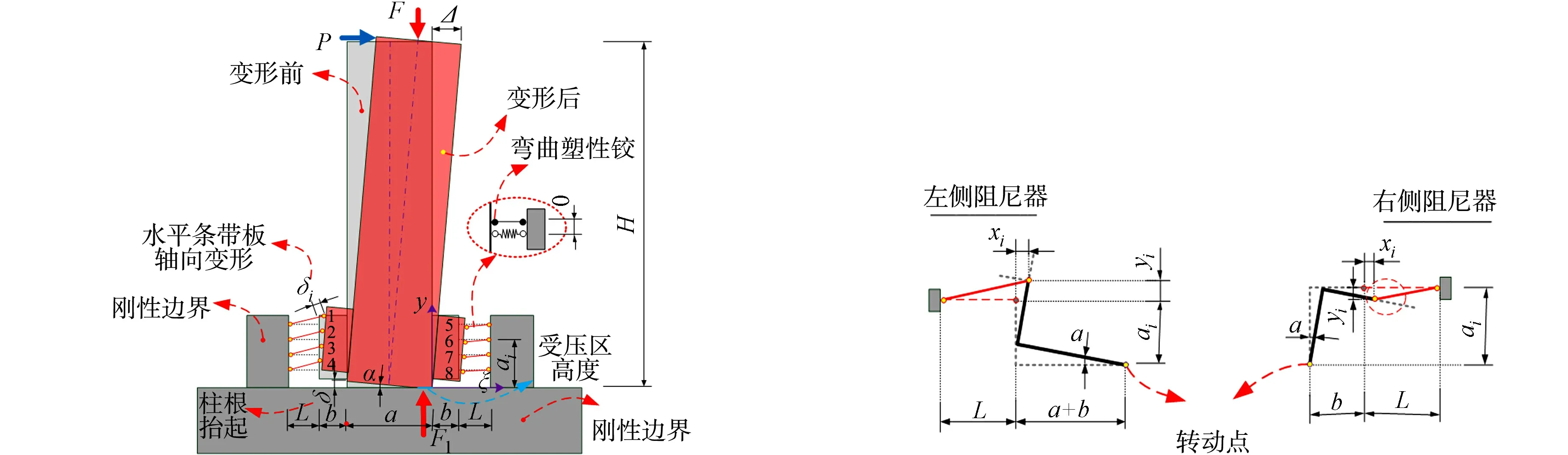
(a) 整体模型 (b) 局部几何关系示意图图13 IRR柱简化受力分析模型Fig.13 Simplified force analysis model of IRR column
塑性变形充分发展的前提下,所有塑性铰均可发挥其塑性弯矩,由于条带板截面相同,塑性弯矩大小一致,因此,弯曲变形不影响竖直方向的力平衡.
由竖直方向的力平衡计算,可得柱底对承台的局部压力为
Fl=∑Fyv+F,
(2)
Fyv=Fyisinαi.
(3)
式(2),(3)中:Fl为柱底承台局部压力;Fyv为阻尼器条带板的屈服承载力在竖直方向的分量;αi是水平条带板轴线与水平线的夹角;i是阻尼器条带板的编号;Fy是阻尼器条带板的轴向拉压屈服承载力,取Fy=fydB,B是阻尼器水平条带板的截面高度.
对于图13中柱脚抬起侧,即左侧的钢板阻尼器水平条带板轴线与水平线的夹角计算式为
xi=aisinα+(a+b)(1-cosα),
(4)
yi=ai(cosα-1)+(a+b)sinα,
(5)
(6)
式(4),(5)中:a=Δ/H,根据试验和有限元分析结果,IRR柱达到峰值承载力时,a近似取1/20.
对于图13中柱脚抬起另一侧,即右侧的钢板阻尼器水平条带板轴线与水平线的夹角计算式为
xi=aisinα+b(cosα-1),
(7)
yi=ai(1-cosα)+bsinα,
(8)
(9)
将IRR柱的设计参数代入式(1)~(9)中,即可求得承台的局部压力.
4.2 局部压应力最大值
得到局部压力后,计算局部压应力最大值需要确定两个因素,即局压区面积和压应力分布规律.假设承台沿加载方向的局部受压区高度为ξ,局部压应力分布曲线用多项式表达.局部受压区应力分布简化图,如图14所示.

图14 局部受压区应力分布简化图Fig.14 Simplified model of stress distribution in local compression zone
根据有限元计算结果,确定峰值荷载状态下,不同参数试件局部受压区域受压区高度的有限元计算结果,如图15所示.由图15可知:柱底承台局压范围内的受压区高度跟阻尼器厚度和轴压比大致呈线性关系,具体数值在12~17 mm.经双参数线性拟合可得ξ的计算式为
ξ=10.93n-0.054 38d+12.2.
(10)
式(10)中:0.1≤n≤0.4;8 mm≤d≤20 mm.
假设受压区的压应力分布曲线形状分别为三角形、二次抛物线形、三次抛物线形和矩形.承台局部压应力最大值的计算式为
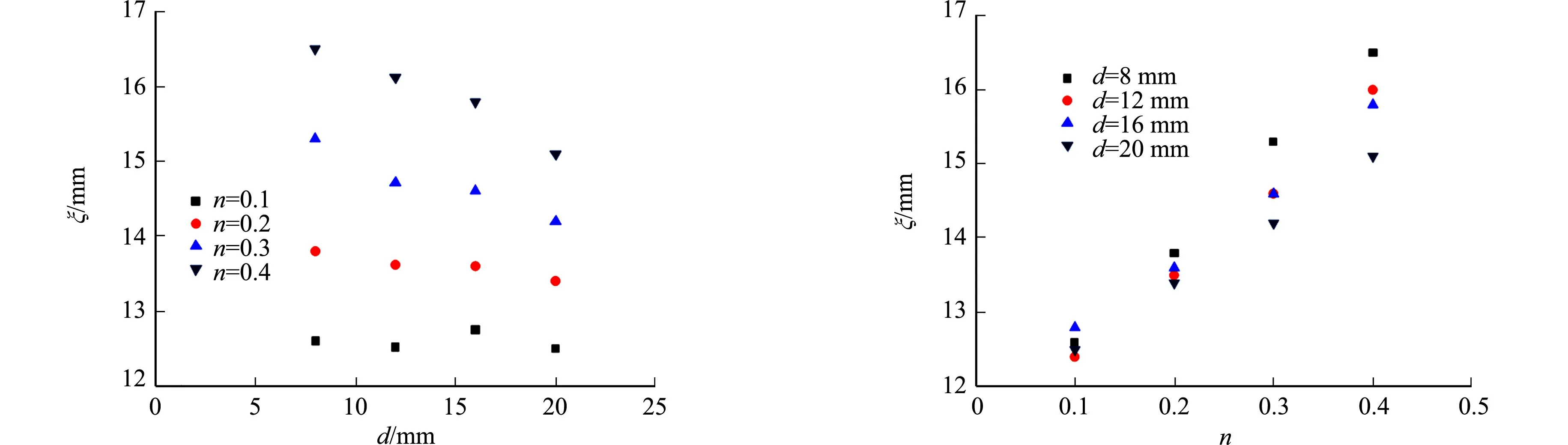
(a) 阻尼器厚度 (b) 轴压比图15 局部受压区受压高度的有限元计算结果Fig.15 Calculation results of compression height of local compression zone on finite element analysis

(11)
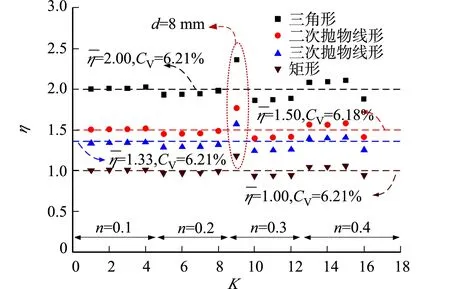
图16 η的计算结果Fig.16 Calculation results of η
式(11)中:k为压应力分布系数,三角形、二次抛物线、三次抛物线和矩形的压应力分布系数分别取1/2,2/3,3/4,1.
定义承台最大局部压应力计算值与有限元分析值的比值η为
η=σcal/σFEA.
(12)
式(12)中:σcal为式(1)~(11)计算所得承台最大局部压应力;σFEA为有限元模型的最大局部压应力计算结果.

由图16可知:假设承台局部压应力分布曲线为三角形、二次抛物线、三次抛物线和矩形,计算得到η的平均值分别为2.00,1.50,1.33和1.00;采用矩形分布假设计算所得的结果与有限元吻合良好,其离散系数仅为6.21%,可供工程实践和后续研究参考.
5 结论
采用有限元方法,对IRR柱柱底承台承载力极限状态下局部压应力的分布规律进行研究,得到4点主要结论.
1) 轴压比是影响试件柱底承台压应力大小的主要参数.随着轴压比的增大,柱底承台压应力值显著增大.当试件轴压比从0.1增加到0.4时,承台局部压应力最大值增加了142.9%~172.9%.
2) 阻尼器厚度从8 mm增加到20 mm时,承台局部压应力最大值增加了14.3%~41.2%.
3) 承台材料的弹性模量对局部压应力分布影响不显著.
4) 通过与有限元计算结果的对比,提出IRR柱柱底承台局部压应力计算模型,可为性能可恢复摇摆柱的承台局压设计提供参考.

