量子力学纯态表象与混合态表象间的积分变换
孟祥国
(聊城大学 山东省光通信科学与技术重点实验室、物理科学与信息工程学院,山东 聊城 252059)
由狄拉克提出的表象变换理论在量子力学中是一个基本的课题[1],通常来说,它指的是两个不同的量子力学纯态表象之间的变换,例如,由坐标表象变换到动量表象
(1)
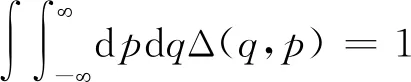
(2)
本文在纯态表象(坐标表象|q〉和动量表象|p〉)和混合态表象(Weyl-Wigner表象)之间建立一种新型积分变换,并讨论它的具体应用.利用有序算符内的积分法,坐标表象和动量表象的完备性关系可表示为[3]
(3)
这样,Wigner算符Δ(q,p)的正规排序为
(4)
(5)
利用有序算符内的积分法,可证明算符Δ(q,p)满足如下完备性关系
(6)
从这个意义上,说明Δ(q,p)能构成一个混合态表象.因此,根据Δ(q,p)的完备性关系,任何算符ρ都能被展开(即Weyl展开)
(7)
或者利用式(5)和(7),算符ρ也可表示
(8)
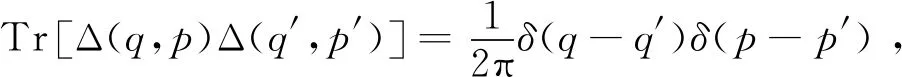
1 算符|q〉〈q|p〉〈p|和Δ(q,p)间的积分变换
当把经典函数eλq+σp量化为一个算符时,可采取如下三种方法
eλq+σp=eλqeσp→eλQeσP, (Q-排序),
eλq+σp=eσpeλq→eσPeλQ, (P-排序),
eλq+σp→eλQ+σP, (Weyl-排序),
(9)
式中[Q,P]=i (ћ=1).这样,相应的三种量子化方案分别表示为
(10)
其中符号Q指的是所有的坐标算符Q都站在所有动量算符P的左侧,而符号P指的是所有的动量算符P都站在所有的坐标算符Q左侧,而Weyl排序依赖于Wigner算符,即
(11)
若用符号
来标记Weyl排序,则算符eλQ+σP的Weyl排序可表示为
(12)
把式(12)代入式(11)并利用有序算符内的积分法,可得到Wigner算符Δ(q,p)的Weyl排序,即[8]
(13)
值得指出的是,算符Q和P在以上三种排序中都是对易的.进一步,利用式(13)及其傅里叶变换,可导出Wigner算符的原始定义式,即
(14)
利用Weyl排序内的积分法可以建立以上三种排序之间的联系,即
(15)
再利用式(13),我们有
(16)
类似地,可有
(17)
由式(16)和(17)可见,坐标和动量表象和Wigner表象之间满足新的积分变换,其积分核为e±i2(p-p′)(q-q′).因此,式(16)和(17)给出的积分变换的逆变换分别为
(18)
2 算符ρ的Wigner函数与Tr(ρ|q〉〈p|)/Tr(|q〉〈p|)的新关系
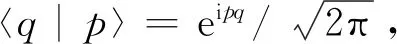
(19)
(20)
相应地,其逆变换为
(21)
这个积分表达式为计算算符ρ的Wigner函数提供了一种新的方法.例如,对一个压缩参量为λ的单模压缩算符ρλ=e(a†2-a2)λ/2[9,10],它的坐标本征态表示为[11]
(22)
由此式直接推导出
(23)
把式(23)代入式(21),可推导出压缩算符ρλ的Wigner函数,即
(24)
另一方面,当把式(24)代入式(7)时,可得到算符ρλ的Weyl排序形式,即
(25)
3 菲涅尔算符的Weyl经典对应
对于菲涅尔算符[12,13]
(26)
其中AD-BC=1,它对应于经典光学中的菲涅尔光学变换,利用算符eiλPQ的P排序表示
eiλPQ=P[exp{-i(e-λ-1)PQ}],
(27)
可得到
(28)
结合式(26)和式(28),我们有
(29)
进而,把式(29)代入式(21)并经过简单的积分运算,可得到菲涅尔算符F的Weyl经典对应
(30)
4 分数阶压缩算符
特殊地,当B=coshθ,C=-coshθ,A=sinhθ,D=-sinhθ时,则式(29)的右边变为
(31)
(32)
另一方面,由式(8)可得到分数阶压缩算符的正规排序表示,即
(33)
(34)
(35)
综上,借助有序算符内的积分法,本文在纯态表象(坐标表象和动量表象)和混合态表象(Weyl-Wigner表象)之间建立了一种新的积分变换,并由此提出了一种计算系统密度算符Wigner函数的新方法.此外,给出了菲涅尔算符的Weyl经典对应和分数阶压缩算符的正规排序及其简洁表示.

