三种GNSS 模糊度解算方法性能的对比分析

汪 鑫 吴汤婷 徐兆祥 王建敏

（1.东华理工大学 测绘工程学院 江西南昌 330013；2.长沙市规划勘测设计研究院 湖南长沙 410000；3.南京白鲨测绘科技有限公司 江苏南京 210038）

1 引言

自整数最小二乘方法被用于模糊度解算领域中来，以LAMBDA 算法[1]为代表的基于模糊度协方差矩阵降相关和球形离散搜索的模糊度解算方法成为研究的热点。其中，文献[2]对LAMBDA 算法做了详细理论分析。文献[3]等通过上下三角过程构造的联合去相关算法可以有效地降低模糊度之间的相关性。文献[4]等首次提出基于排序的QR 分解降相关算法，其后文献[5] 将该策略进行改进并应用到MLAMBDA 算法中，大大提高了解算效率。由于整周模糊度的解算等价于格理论上的最近向量问题，因此有学者从格基规约角度对模糊度解算进行研究。文献[6]等首次将LLL 规约算法用于模糊度解算，并指出多维高斯整数降相关方法与LLL 规约算法原理等价。文献[7]从理论上证明了格基规约可以有效的减少搜索候选点数。文献[8]证明了格基规约与降相关之间的等价性。文献[9]将降相关方法统一至格理论框架下，从理论上证明了不同降相关方法的性能。文献[10-13]对LLL 算法的规约过程进行了改进，提高了规约效率。

为研究SEQR 算法、LAMBDA 算法和LLL 规约算法三种算法的性能，本文采用模拟和实测数据对降相关领域中的SEQR 算法和LAMBDA 算法，基于格基规约理论的LLL 算法，从规约时间、搜索时间、总体时间和条件数四个方面进行了研究分析，以期得出相应的结论，为相关研究提供参考。

2 基本原理

2.1 LLL 规约算法

根据整数最小二乘原理，模糊度的整数估计准则为[1]

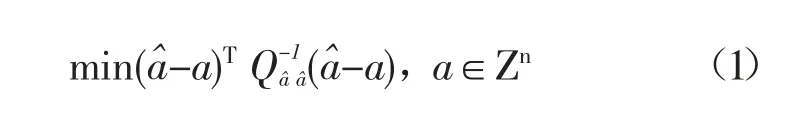
式（2）中，B 为上三角矩阵。

把式（2）代入式（1），可得式（3）中，是一个常数。

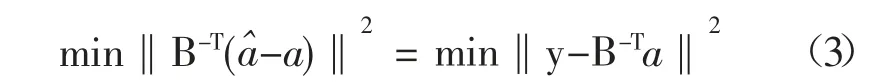
式（3）也被称为最近向量问题，是格基规约理论中一个著名的难题，常采用LLL 算法进行格基规约处理。

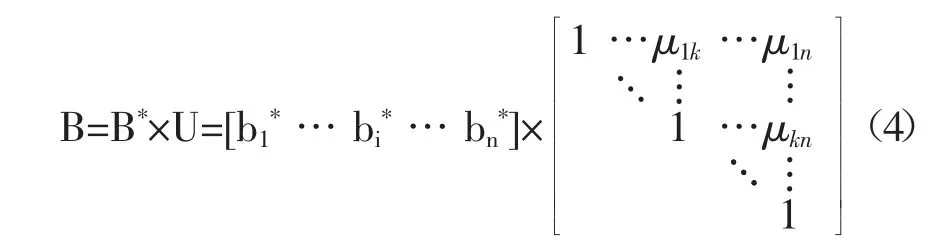
LLL 规约后 和U 中的元素应满足下面两个条件：

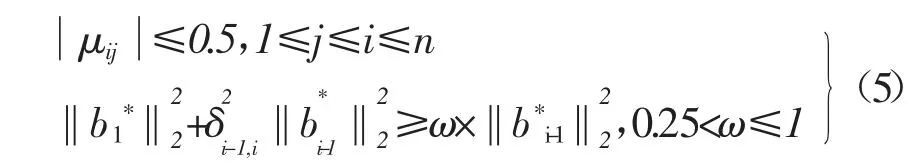
式（4）中，B*=[b1*… bi*… bn*]，其中

式（5）中，上式称为尺度规约，下式称为基向量交换，其中称为规约参数。

2.2 LAMBDA 算法

LAMBDA 算法最早由Teunissen 提出，核心思想是在整数最小二乘估计的基础上，对协方差矩阵 进行Z 变换，通过有效的减少搜索椭球外的节点数，从而提高搜索效率[2]。对 进行 分解，经过高斯降相关解算得到整数Z 变换矩阵。

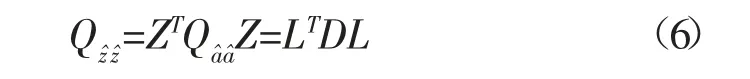
式（7）中，上式称为模糊度协方差矩阵降相关，下式称为条件方差的排序。

2.3 排序QR 分解算法

排序QR 分解算法思想最初是由Xu 等人提出并将其运用在模糊度降相关领域中，后由Dirk Wubben 等[14]用于无线通信领域，并首次将其称为排序QR 分解算法（Sorted QR decomposition, SEQR），一般简称SEQR 算法。

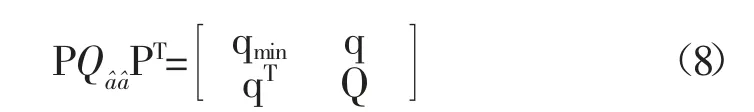
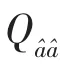
按照下式对子矩阵Q 进行更新计算

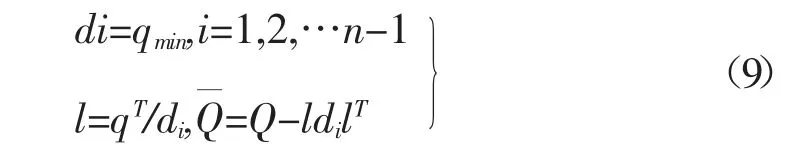
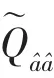
3 评价指标

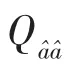
4 实验与分析

4.1 模拟数据实验

本文模拟实验数据参考的是文献[5]提出的模拟方法，浮点解的构造为

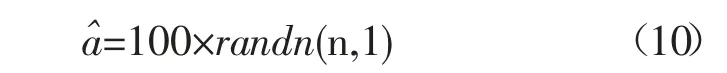
式中，randn 为MATLAB 内部函数，表示随机生成n个服从标准正态分布的元素。

协方差矩阵 由下三角Cholesky 分解构建，即

式中，L 是单位下三角矩阵，L 中的元素）服从标准正态分布，D 是对角矩阵，主对角线元素为（10, 10, 10,0.1, 0.1, … ,0.1）。

实验分别模拟了10 维、20 维、30 维三组数据，每组各模拟了100 历元的模糊度数据，用以分析不同维度下三种算法的性能表现。

10 维情况下100 历元模拟数据的平均解算结果见表1。从表1 可以看出，SEQR 算法的降相关时间要小于LLL 算法的解算结果，但两者的平均搜索时间基本一致，LAMBDA 的降相关时间相比于其余两种算法效果较差，但搜索时间比其余两种算法效果相对较好。三种算法的条件数基本一致。100 历元三种算法解算结果的累积分布函数如图1 所示，图1 中结果与表1 结果趋势一致。

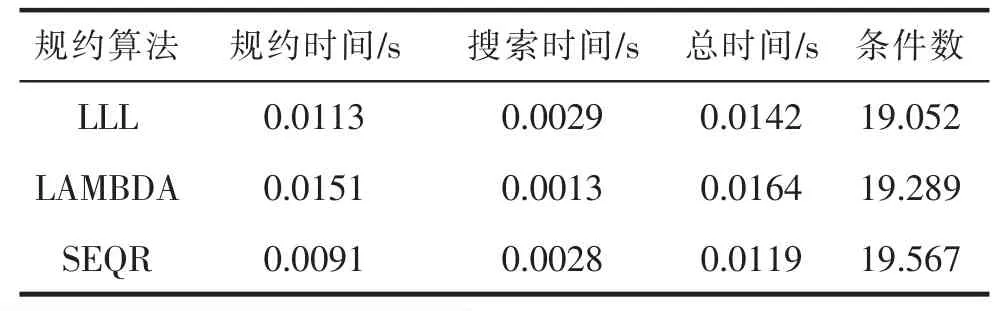
表1 100 历元三种算法10 维平均解算结果

20 维情况下100 历元三种算法的平均解算结果见表2。在20 维情况下，LLL 算法的规约效率最高，但搜索时间相较于其余两算法效果较差。在总体效率上，LLL 算法比SEQR 算法效率略低，二者均高于LAMBDA 算法。在条件数上SEQR 算法最小，即矩阵的对角化程度要比其余两种算法较好。20 维100 历元三种算法解算结果的累积分布函数如图2所示，图2 与表2 的结果趋势一致。

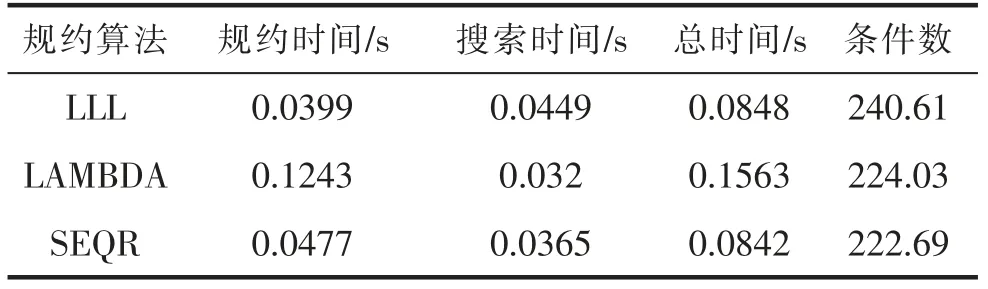
表2 100 历元三种算法20 维平均解算结果

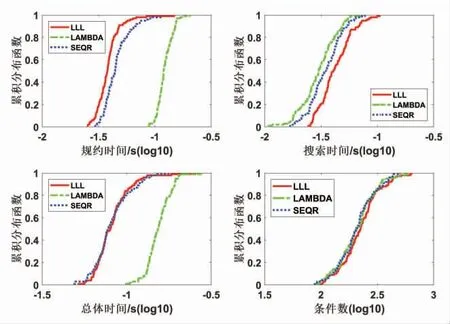
图2 100 历元三种算法20 维累积分布函数图（log10 表示坐标轴取对数）

30 维模拟数据的平均解算结果见表3，30 维模拟数据的累积分布函数如图3 所示。30 维情况下三种算法的结果与20 维基本一致，LLL 算法的规约效率最高，搜索效率上，SEQR 算法最高，总体性能上LLL 算法比SEQR 算法略低，二者均高于LAMBDA算法。由于维度较高，矩阵的病态性上升，三种算法在降相关后的条件数仍然较大。

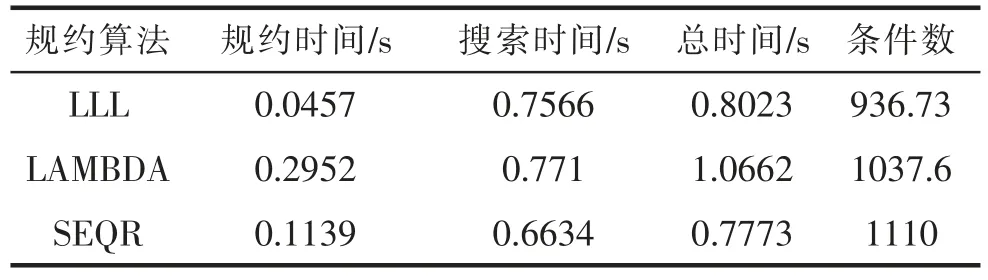
表3 100 历元三种算法30 维平均解算结果

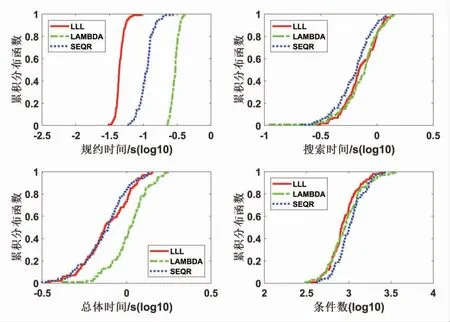
图3 100 历元三种算法30 维累积分布函数图（log10 表示坐标轴取对数）

4.2 实测数据实验

为进一步比较三种算法的性能，采用一组静态观测数据进行实验，该组数据使用司南M300-Pro 接收机采集，基线长29.5km，采样间隔1s。实验取前100 历元的GPS+BDS 单历元处理结果。

三种算法实测数据100 历元的平均解算结果见表1，三种算法实测数据的累积分布函数如图4 所示。从图表的结果来看，在这组实验中，SEQR 算法的总体效率在三种算法中最高。LLL 算法在这组实验中，规约效率最差，由于搜索效率比LAMBDA 算法高，导致最终的整体解算时间相较于LAMBDA 算法效果更好。LLL 算法在这组实验中规约性能较差原因在于该组数据结构较大，LLL 算法在规约过程循环了多次以满足尺度规约条件，因此造成规约时间较其他两种算法更大。这组实验中，SEQR 算法的条件数相较于其他两种算法更小。

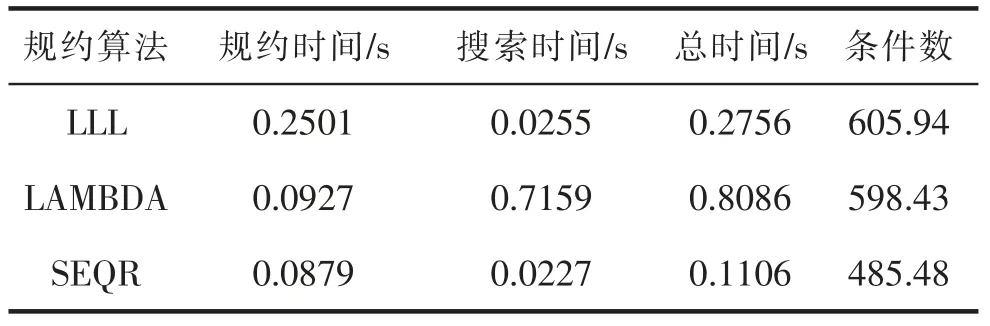
表4 100 历元三种算法实测数据平均解算结果

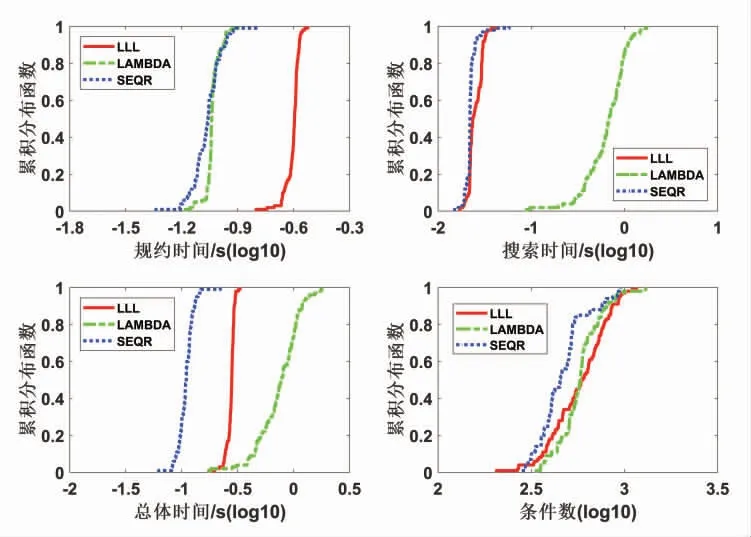
图4 100 历元三种算法实测数据实验累积分布函数（log10 表示坐标轴取对数）

5 结论

本文利用三组模拟数据实验和一组实测数据实验对LLL、LAMBDA 和SEQR 算法的性能进行了比较分析，结果表明SEQR 算法的总体性能最优，LLL算法其次，LAMBDA 算法总体性能在本文中相对较差。主要原因在于SEQR 算法在降相关过程中对条件方差进行了排序，用较少的降相关过程获得了一个更有利于搜索的降相关矩阵。LLL 算法的规约性能与数据的结构有关，在模拟数据实验中LLL 算法的规约性能效果相对较好，但在实测实验中效果相比于其他两种算法较差。LAMBDA 算法采用的分解方式为分解，因此在本文模拟数据中的降相关效率相对较差，在实测实验中由于降相关的矩阵条件方差的排序效果不稳定，所以导致搜索性能较差。综上所述，在进行GNSS 模糊度解算时，采用SEQR 算法进行降相关解算更有优势。