采样过滤下的时空热点查询

李艳云，牛保宁，康家兴

(太原理工大学 信息与计算机学院，太原 030024)

时空热点是指交通流量较大、居民来往次数较多的时空区域。不同于二维平面区域，时空热点是特定的三维空间,是具有时间信息的热点地理区域，如7:00-9:00的长风街是时空热点，但其他时间段的长风街有可能不是时空热点。本文以出租车轨迹数据为对象，通过对其进行时空分析[1]和数据挖掘[2]，从而发现城市时空热点[3-4]。城市时空热点发现对城市规划[5]、交通管理、打击犯罪等一系列基于位置的服务有重要的参考价值。

为此，针对第一阶段map-reduce严重耗时及资源空闲的问题，本文提出一种对轨迹数据采样的方法S-RSampling.通过分析轨迹数据随时间的变化，得到其分布规律，确定采样分层数和采样比例。在每条轨迹数据映射成〈k,v〉时，根据其分层数、分层比例进行采样，大幅度降低查询时间。为降低任务空闲等待时间，在k值相同的〈k,v〉聚合时，对所有〈k,v〉随机采样，缓解数据分布不均匀的影响，减少资源等待时间。针对第二阶段map-reduce计算浪费的问题，本文提出一种阈值过滤方法TFiltering.根据单元格属性值的分布，动态确定阈值T，并将属性值从大到小排序top-T的立方单元格作为热点候选集，仅计算热点候选集中立方单元格的热度值，从而减少计算浪费，提高时空热点查询效率。本文的创新点如下。

1) 提出一种对轨迹数据采样的方法S-RSampling.在轨迹数据映射成〈k,v〉时，根据轨迹数据分布规律分层采样，大幅降低查询时间；在k值相同的〈k,v〉聚合时，为减少资源等待时间，对所有〈k,v〉随机采样，缓解数据分布不均匀的影响。

2) 提出一种阈值过滤方法TFiltering.探索出一种确定阈值的方法，依据立方单元格属性值的分布规律,动态确定阈值T；选择热点候选集，将属性值从大到小排序top-T的立方单元格，作为热点候选集，减少计算浪费，提高时空热点查询效率。

1 研究现状

时空热点查询在ACM SIGSPATIAL GISCUP 2016编程竞赛[11]中被要求提出高效、快速的算法，以实现对纽约市出租车轨迹数据的热点分析，开发运行于Spark分布式集群的map-reduce算法。目前，对于这类高效时空热点查询的研究并不多，其思想都是基于Spark分布式计算框架和Getis-Ord公式的热度统计法。根据应用场景不同，可以将现有算法分为两类，一类是无约束条件的查询，这类查询不需要用户指定查询参数,而是对全部轨迹数据进行一次性计算；另一类是有约束条件的多参数查询，这类查询可以由用户指定查询参数，如地理范围、时间范围等，针对不同的查询参数处理不同的轨迹数据，返回用户指定个数的时空热点。

无约束条件类算法中，NIKITOPOULOS[12]提出BigCAB算法，严格遵循热度统计法思想，将每个立方单元格作为RDDs元素，每一步都精确计算。SALLES et al[13]提出的K-H-CP算法在BigCAB算法基础上将城市时空分区，将分区作为RDDs元素。因为大部分立方单元格及邻居作为一个RDDs元素被存储在同一节点中，所以在计算邻居间相互影响时，节点间的通信开销降低。PARAS et al[14]提出的STG算法与K-H-CP算法类似，该算法通过将时空邻接的立方单元格组成25×25×25的组。一个组的立方单元格存储在同一节点上，从而降低节点间的通信开销。K-H-CP和STG算法都是通过改变RDDs元素来降低节点间的通信开销，均为精确算法。不同于上述三个算法，SHANGFU et al[15]提出的SR-K-M算法是在BigCAB算法的基础上加了过滤和细化策略。由于过滤掉大部分立方单元格，所以计算量和网络通信开销大幅度降低。

以上这些算法都需要对全部轨迹数据进行计算，由于轨迹数据量巨大，所以遍历一遍轨迹数据是造成整个查询过程耗时的主要原因。而且对于数据分布不均导致的资源空闲等待，以及计算大量无用立方单元格造成计算浪费的问题，上述算法没有相应的优化。

有约束条件的多参数查询算法如康家兴等[16]提出的多参数城市时空热点查询，该算法对轨迹数据建立三维网格索引，能灵活地满足不同的查询。根据用户指定的不同参数，处理不同的轨迹数据，返回用户指定个数的时空热点。虽然处理不同的轨迹数据，但仍要对相应的全部轨迹数据进行一次遍历，当所需的轨迹数据量较大时，耗时问题仍然存在。而且对于计算浪费问题，该算法没有相应优化策略。

2 预备知识

2.1 Getis-Ord公式

Getis-Ord统计量常用来进行热点分析，其计算公式如下：

(1)

(2)

(3)

(4)

2.2 热度统计法

热度统计法是将城市时空按设定好的单元格粒度，划分为若干相同大小的立方单元格，根据坐标映射公式，将轨迹数据映射到立方单元格中，统计立方单元格的属性值，利用Getis-Ord公式计算出各立方单元格的热度值。

出租车轨迹数据p记录了乘客下车经纬度、下车时间点以及乘客数等有用信息。将这些重要信息提取出来用(plon,plat,pt,pv)表示，(plon,plat)表示下车位置经纬度信息；pt表示下车时间点，记录了年、月、日、和时间等信息；pv表示乘客数。

轨迹数据p到立方单元格坐标(x,y,t)(x,y分别表示经纬度坐标轴，t表示时间轴)的映射公式为：

{p→(x,y,t)|x=⎣plon/x0」,

y=⎣plat/y0」,t=⎣pt/t0」} .

(5)

式中：x0，y0，t0分别为单元格经度、纬度和时间轴划分粒度[16]。

热度统计法的大致流程如图1所示。第一阶段map-reduce：map函数根据坐标映射公式将每条轨迹数据映射到立方单元格中，即将轨迹数据处理成〈k,v〉(其中k表示单元格坐标(x,y,t)，v表示乘客数)；reduce函数将k相同的〈k,v〉聚合得到〈k,vnum〉，计算出各立方单元格的属性值vnum(即公式(1)中的xj).

图1 基于Getis-Ord公式的热度统计法流程图Fig.1 Flowsheet of heat statistics method based on Getis-Ord formula

3 优化方法

针对现有算法存在的第一阶段map-reduce耗时且效率低，以及第二阶段map-reduce计算浪费的问题，本文提出一种对轨迹数据采样的方法S-RSampling和一种阈值过滤方法TFiltering.为了方便后续理解，先解释现有算法第一阶段map-reduce的具体步骤。

1) 从hdfs(即Hadoop分布式文件系统)读取轨迹数据。

2) 用map()函数将每条轨迹数据根据坐标映射公式处理成〈k,v〉的形式。相同k对应的〈k,v〉不止一个，因为多条轨迹数据会映射到同一个立方单元格中。

3) 通过reduceBykey()函数将k值相同的〈k,v〉聚合成〈k,vnum〉.〈k,vnum〉代表坐标为k的立方单元格属性值为vnum.

由于算法是查询top-k时空热点，只需对单元格的热度值进行排序，不需要计算出每个单元格的实际热度值，所以不一定要对全部轨迹数据进行处理。另外，由于轨迹数据量巨大，每条轨迹被映射成〈k,v〉后，数据量仍然很大，而且数据分布不均匀导致计算效率降低。为此，本文提出S-RSampling方法。该方法分为两步，第一步是在步骤2)之前，对轨迹数据进行规律采样。具体地，分析轨迹数据随时间的分布规律，根据其分布规律确定采样分层数及采样比例，按分层数和比例对轨迹数据进行分层采样，使得样本能够反映全部轨迹数据的分布。第二步是在步骤2)之后，对〈k,v〉数据进行随机采样。具体地，通过Sample算子对〈k,v〉数据进行随机采样，每个〈k,v〉被采到的概率相同。

3.1 S-RSampling方法

S-RSampling方法分为两步，第一步是在轨迹数据映射前，根据轨迹数据分布规律，对轨迹数据进行分层采样，称为规律采样。第二步是在轨迹数据映射后(即map后)，对〈k,v〉数据进行随机采样，称为map随机采样。

3.1.1规律采样

本文根据时间找到轨迹数据分布规律并依据分布规律进行采样。在针对同样数据集的其它热点查询任务中，直接根据其分布规律进行采样，极大地降低查询时间。出租车轨迹数据包含下车经纬度、下车时间点以及乘客数等字段。根据下车时间点字段将轨迹数据以1 h为单位分割成24份，分别统计每个时间段内的乘客数。具体步骤如下：

1) 从hdfs读取轨迹数据；

2) 分割轨迹数据的每个字段；

3) 取出下车地点经纬度、时间、乘客数等重要信息；

4) 根据时间字段的空格分割数据，并统计每个时间段内的乘客数。

对12个月的数据进行实验，取平均值得到一天(24 h)中不同时间段的轨迹数量，从而得到轨迹数据随时间的分布规律，如图2所示。横轴代表时间，纵轴代表轨迹数据数量。实验中不会特殊考虑周末节假日等轨迹数量峰值的时间段情况。这是由于一方面将轨迹数据中的时间字段转换成周末节假日等信息需要大量的额外消耗；另一方面周末节假日的轨迹数量本来就比较多，按比例采样时周末节假日数据被采到的概率本来就大，所以不需要特殊处理周末节假日的数据。

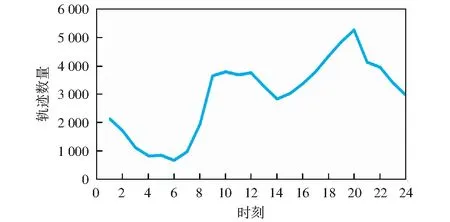
图2 轨迹数据数量随时间分布图Fig.2 Distribution of trajectory data over time

根据分布图的极小值点，本文将轨迹数据根据极小值点对应的时间划分为l1,l2,…,lm+1(m为极小值个数)多层，统计各层轨迹数据数量之比r1∶r2∶…∶rm+1.规律采样策略对l1,l2,…,lm+1层的轨迹数据进行r1∶r2∶…∶rm+1分层采样，使得样本符合原始轨迹数据的分布规律，保证使用小数据集也能得到精确的结果。规律采样过程如算法1.

算法1规律采样算法

输入：不同层的轨迹数据和采样比例

输出：分层采样后的轨迹数据

/*从hdfs读取不同层的轨迹数据，rdd1、rdd2和rdd3为不同层数据*/

1) val rdd1 = sc.textFile ("hdfs://master:9000 /input/2015green/1green")

2) val rdd2 = sc.textFile ("hdfs://master:9000 /input/2015green/3green")

3) val rdd3 = sc.textFile ("hdfs://master:9000 /input/2015green/6green")

/*对不同层数据进行分层采样，并合并，以便后续将不同数据一同处理，rdd5为合并后的数据集*/

4) val rdd4 = rdd1.sample(false,r1).union (rdd2.sample(false,r2))

5) val rdd5 = rdd4.union(rdd3.sample(false, r3))

6) rdd5.saveAsTextFile("hdfs://master:9000/output/OutputRegular") /*保存数据*/

3.1.2map随机采样

由于轨迹数据量巨大，经过规律采样后〈k,v〉仍旧很多，而且〈k,v〉数据分布不均匀造成计算效率低。本文在第一阶段map后对所有〈k,v〉进行随机采样，减少计算量和资源等待时间。具体地，在第一阶段map之后，通过Sample算子对这一阶段产生的〈k,v〉进行随机采样，实验中通过调整采样率来比较查询结果准确率。map随机采样计算过程描述如算法2.

算法2map随机采样算法

输入：第一阶段map后的〈k,v〉和采样率

输出：采样后的〈k,v〉

1) val conf = new SparkConf().setAppName

2) val sc = new SparkContext(conf)

3) val rdd2 = rdd1.sample(false,r) /*rdd1为算法输入的〈k,v〉，r为采样率*/

4) rdd2.saveAsTextFile("hdfs://master:9000/output/OutputMap") /*保存数据*/

3.2 TFiltering方法

对12个月的数据进行实验，得到立方单元格热度值和数量的长尾分布，如图3所示，横轴代表立方单元格热度值区间(×102)，纵轴代表立方单元格的数量(×104)。如热度值在100到200的立方单元格有16万多个。可以看出，大部分立方单元格的热度值很小，计算这些不可能成为时空热点的立方单元格，无疑会造成计算浪费。

图3 单元格热度值与数量分布图Fig.3 Distribution of cubes,heat and number

3.2.1阈值确定方法

由于立方单元格的热度值越大其属性值通常也较大，所以根据单元格的属性值选择热点候选集。具体地，本文在第一阶段map-reduce后将立方单元格根据属性值从大到小排序得到单元格属性值的分布规律，如图4(数据量为12个月)，横轴代表单元格编号(单元格按属性值从大到小的排序编号)，纵轴代表单元格属性值。计算分布曲线的拐点坐标(xid,yvalue)，并将xid作为阈值基数。

图4 单元格属性值分布Fig.4 Distribution of cubes,value

考虑两种极端情况：一是top-xid个单元格紧密相邻；二是top-xid个单元格互不相邻，互不影响。

第一种情况，属性值排序top-xid的单元格中，除了极少数边界单元格，其余单元格的邻居贡献都能在这xid个单元格中计算得到，所以本文取xid作为阈值，属性值排序top-xid的单元格作为热点候选集。

第二种情况，属性值排序top-xid的单元格中，每个单元格邻居贡献的计算都需要额外的26个邻居单元格，所以本文取27xid作为阈值，属性值排序top-27xid的单元格作为热点候选集。

综合上述两种情况，本文取阈值T为两种极端情况下的平均值(xid+27xid)/2，即14xid.数据集不同，分布曲线就不同，所以阈值T也不同，阈值T随着数据集的不同而动态变化。实验表明，这种阈值选取方法在不同数据集下的算法结果准确率为100%.阈值选取的具体步骤如下：

1) 将单元格按属性值从大到小排序；

2) 得到单元格属性值分布曲线f(x)；

3) 计算曲线f(x)的拐点坐标(xid,yvalue)；

4) 根据T=14xid，计算得到阈值T.

3.2.2热点候选集的选取

在确定了阈值T后，根据单元格属性值和阈值选取热点候选集。具体地，对map随机采样后的数据进行聚合，并对聚合得到的〈k,vnum〉，按vnum值从大到小对立方单元格排序，将top-T的立方单元格作为时空热点候选集。热点候选集选择过程如算法3.

算法3热点候选集选择

输入：map随机采样后的〈k,v〉和阈值T

输出：热点候选集〈k,vnum〉

1) val rdd2 = rdd1.reduceByKey((x,y)=〉x+y) /*对输入的数据rdd1按k进行聚合*/

2) val rdd3=rdd2.sortBy(_._2,false)/*对聚合后的数据rdd2按vnum进行排序*/

3) val rdd4=rdd3.top(T)/*取vnum排序top-T的单元格作为热点候选集*/

4) rdd4.saveAsTextFile("hdfs://master:9000/output/OutputFilter") /*保存数据*/

4 实验分析与验证

本文实验运行在Spark2.2.0集群，集群有2个实际工作节点，每个工作节点有2个核，4 G内存。实验数据为2015年的纽约市出租车数据，约15×108条记录，共计约24 G，覆盖范围为纬度40.5 N-40.9 N，经度73.7 W-74.25 W.本文实验中立方单元格划分了约36×104个，经纬度和时间方向网格粒度分别为：200 m、200 m和2 h.实验评价指标为结果准确率和查询响应时间。为了在实验结果中方便书写，这里将规律采样、map随机采样和阈值过滤分别用符号SS、RS和TF表示。

4.1 规律采样

为了比较不同采样率下算法的查询响应时间和结果准确率，本文进行了多种规律采样率下的对比实验。通过实验发现，在采样率为10%的情况下，查询响应时间和结果准确率达到较好的平衡，实验结果如表1所示。

表1 规律采样采样率选取Table 1 Selection of regular sampling rate

为了验证规律采样的有效性，本文分别对BigCAB算法与加入SS(采样率为10%)的BigCAB算法、STG算法与加入SS(采样率为10%)的STG算法进行对比实验。在不同数据量下对查询响应时间进行比较，实验结果如图5所示(横轴表示数据量，以月份数量代表数据量大小，纵轴表示查询响应时间，下同)。加入SS的BigCAB算法较BigCAB算法查询响应时间平均降低34.0%，最大降低42.3%；加入SS的STG算法较STG算法查询响应时间平均降低34.8%，最大降低41.0%.

这是因为，本文根据分层数和分层比例对原始轨迹数据进行合理采样，使采样得到的数据能较好地代表原始数据。从而，在不降低查询结果准确率的基础上，大幅减低查询响应时间。

图5 规律采样实验结果Fig.5 Experimental result of regular sampling

4.2 map随机采样

为了比较在第一阶段map后，随机采样在不同采样率下算法的查询响应时间和结果准确率，本文在无规律采样的基础上进行了多种随机采样率下的对比实验。通过实验发现，在采样率为10%的情况下，查询响应时间和结果准确率达到较好的平衡，实验结果如表2所示。

表2 map随机采样采样率选取Table 2 Selection of map random sampling rate

为了验证map随机采样的有效性，本节对BigCAB算法以及加入各优化策略的BigCAB算法、STG算法以及加入各优化策略的STG算法进行对比实验(采样率均为10%)。在不同数据量下比较查询响应时间，实验结果如图6所示。加入RS的BigCAB算法较BigCAB算法查询时间平均降低25.7%，最大降低35.2%；加入SS和RS的BigCAB算法较BigCAB算法查询时间平均降低43.7%，最大降低52.3%；加入RS的STG算法较STG算法查询时间平均降低25.2%，最大降低31.0%；加入SS和RS的STG算法较STG算法查询时间平均降低43.3%，最大降低49.5%.

因为规律采样后的数据较好地代表了原始轨迹数据，映射后的〈k,v〉数据也具有代表性。考虑到需要降低查询响应时间，本文仅对〈k,v〉数据进行简单的随机采样。所以能在查询结果准确率不下降的情况下，减少查询响应时间。

图6 map随机采样实验结果Fig.6 Experimental result of map random sampling

4.3 阈值过滤

为了验证阈值过滤的有效性，本文对BigCAB算法与加入各优化策略的BigCAB算法、STG算法与加入各优化策略的STG算法(采样率均为10%)在不同数据量下进行查询响应时间对比实验，实验结果如图7所示。加入TF的BigCAB算法较BigCAB算法查询响应时间平均降低31.3%，最大降低43.3%；加入SS、RS和TF的BigCAB算法较BigCAB算法查询响应时间平均降低55.4%，最大降低58.7%；加入TF的STG算法较STG算法查询响应时间平均降低30.5%，最大降低43.0%；加入SS、RS和TF的STG算法较STG算法查询响应时间平均降低54.9%，最大降低58.3%.

由于热点区域周围通常也较热，热点单元格不可能存在于热度值都小的区域。所以，存在大量不可能成为时空热点，且对邻居单元格的贡献没有意义的单元格。本文通过阈值过滤，将这些无用的立方单元格过滤，减少计算浪费，从而在查询结果准确率不降低的情况下，减少了查询响应时间。

图7 阈值过滤实验结果Fig.7 Experimental result of threshold filter

5 总结与展望

本文针对现有算法对全部轨迹数据遍历耗时巨大，以及单元格热度值与数量呈现长尾分布导致的效率低和计算浪费等问题，提出如下优化方法：一是对轨迹数据采样的方法S-RSampling，一是阈值过滤方法TFiltering.通过对轨迹数据进行规律采样，避免对全部数据的遍历，大幅降低时间消耗。map随机采样减少〈k,v〉数据量，减少shuffle传输开销以及reduce计算量，缓解数据分布不均匀导致计算效率低的问题；找到一种确定阈值的方法，通过阈值过滤选择热点候选集，减少对不可能成为时空热点的立方单元格的计算，避免计算浪费。对于具有相同数据集的热点查询任务，使用上述优化策略能在保证结果准确率的基础上有效降低查询时间。不足之处是邻居贡献的计算耗费存储空间，计算邻居贡献时所需的空间是第一阶段map-reduce后〈k,v〉数据所占空间的27倍，后续将继续研究，找到一种能简化邻居贡献的代替Getis-Ord公式的方法。