张紧器-高压隔水管耦合系统横向振动特性研究

王 川，方海辉，侯 雯，黎 俊，张 鹏

（1.西南石油大学机电工程学院，四川成都610500；2.国家油气钻井装备工程技术研究中心宝鸡石油机械有限责任公司，陕西宝鸡721002；3.成都京东方光电科技有限公司，四川成都610500）

隔水管是深水钻井作业装备中最重要而又最薄弱的部件，关系着深水钻井作业的安全性［1-3］。常规海洋深水钻井作业一般配备大直径隔水管和水下防喷器组。由于油气资源大多集中在深水区域，隔水管总体质量较大，需要采用具有更高承载能力的钻井平台进行作业，致使钻井作业成本大幅度增加。针对深水钻井作业成本过高的问题，业内人士提出用可直接承受井筒压力的高压小直径隔水管替代传统低压大直径隔水管。高压隔水管使用水上防喷器和水下断开系统进行辅助作业［4-5］。许多学者对高压隔水管的动力学响应特性展开了相关研究，如：Lederer等［6］阐述了高压钻井隔水管系统的组成和性能，并详细介绍了高压钻井隔水管与传统钻井隔水管在配置上的差异；Aird［7］阐述了深水水上防喷器和隔水管在海底井口准备、作业和回收的过程；Taklo［8］分析了在2 887.6 m钻井平台上进行首次地面防喷作业的风险管理过程，并得出一些关键性的结论；Childers［9］从隔水管结构、强度以及钻井作业成本等方面对高压隔水管与常规隔水管进行了比较，得到了不同隔水管系统的差异；吕肖等［10］建立了深水高压隔水管力学模型并进行分析，得出隔水管材料、钻井液密度等因素对隔水管受力状态的影响规律；苏堪华等［11］基于材料力学理论，建立了高压隔水管的准静态力学分析模型和内外压力计算模型；向正新等［12］考虑波浪、海流载荷和地基反力等因素，建立了深水隔水管-井口耦合系统力学模型，并分析了张紧力和平台偏移对隔水管力学行为的影响规律；张慎颜等［13］建立了深水钻井平台-张紧器-隔水管耦合动力学模型，对有、无张紧器作用下的耦合系统进行了静力学分析，同时考虑平台纵荡运动，对有、无张紧器作用下的耦合模型进行动力学分析。由上可知，上述文献没有考虑高压隔水管内部高压流体以及张紧器参数等因素对隔水管横向振动的影响。

针对目前国内外学者主要对高压隔水管进行静力学分析，没有考虑张紧器耦合下高压隔水管的动力学特性，笔者拟对钻井工况下高压隔水管的横向振动特性展开研究。通过建立张紧器-高压隔水管横向振动动力学仿真模型，定量分析隔水管内部高压流体、张紧器耦合作用、海流流速、平台漂移量、张紧器张力比等对隔水管横向振动的影响，旨在为现场钻井操作提供一定的指导。

1 钻井作业工况条件

海上钻井系统如图1所示，它主要包括钻井平台（钻井船）、上挠性接头、水上防喷器、张紧器、高压隔水管、下挠性接头和水下断开系统等。

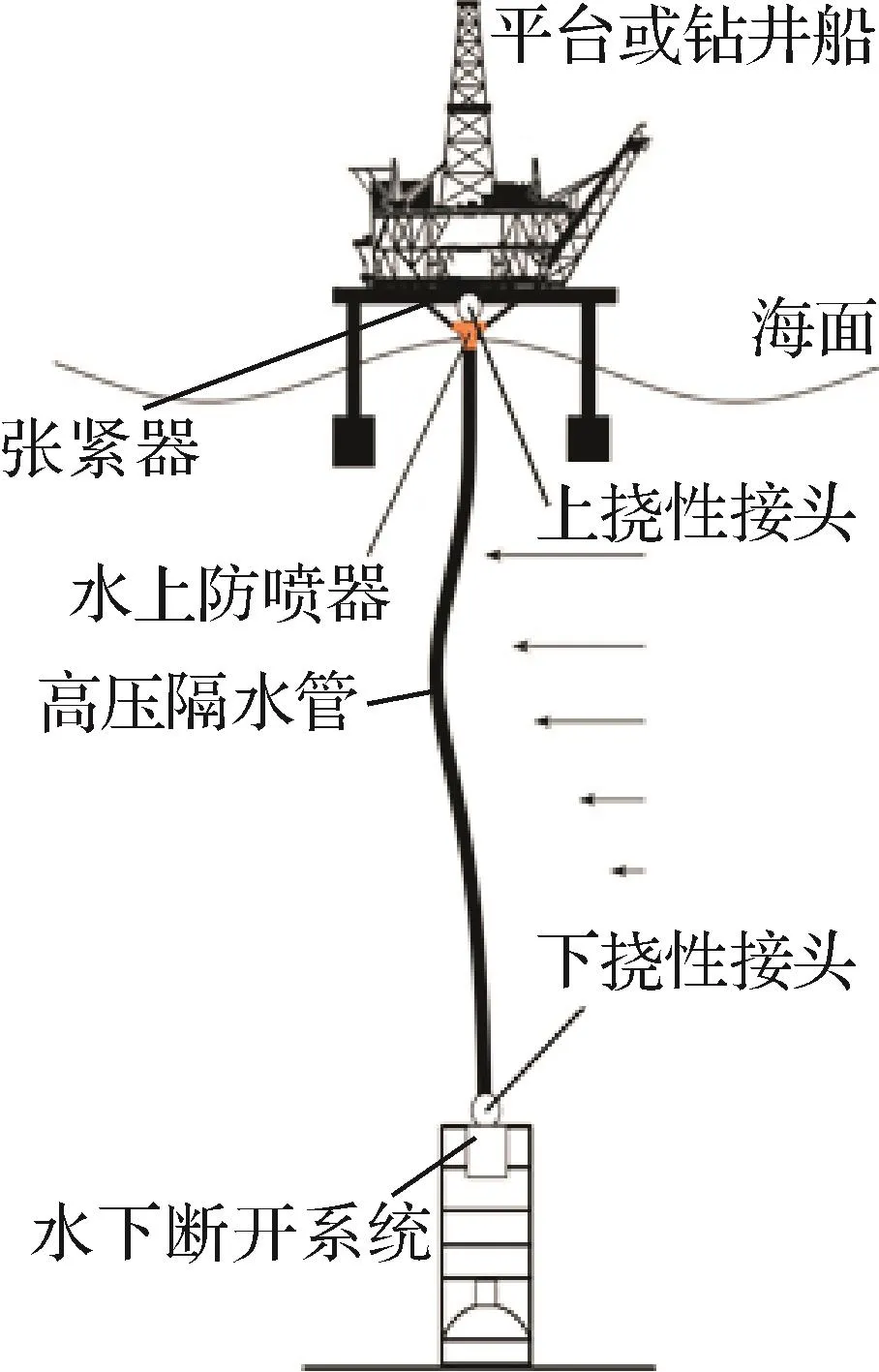
图1 海上钻井系统示意图Fig.1 Schematic diagram of offshore drilling system

高压隔水管在海洋环境中受力情况十分复杂，为了便于分析和计算，作如下假设［14］：

1）高压隔水管系统内的辅助管线对隔水管影响较小，不考虑隔水管系统中辅助管线的影响。

2）高压隔水管由均质、各向同性的线弹性材料制成，即为具有理想性质的圆管；接头与管身具有相同的强度特性。

3）忽略钻柱对高压隔水管的影响。

2 张紧器-高压隔水管耦合动力学仿真模型

2.1 高压隔水管受力分析

在钻井工况下，高压隔水管主要受到水平方向（x向）波浪力和海流力的作用，其下部通过挠性接头与水下断开系统固定。将高压隔水管看作弹性梁，其横向弯曲变形满足材料力学理论中纯弯曲梁的平面假设［15］。在海底任意深度z处，取高压隔水管微元dz，该微元的受力情况如图2所示。

图2 高压隔水管微元受力分析Fig.2 Force analysis of high-pressure riser micro-element

由图2可知，高压隔水管受到的作用力包括张紧器提供的有效张力T、波浪和海流共同作用引起的弯矩M、波浪和海流共同作用引起的外载荷F（z，t）以及管内流体流动产生的惯性力q。弯矩M作用下高压隔水管微元变形势能dUM可表示为：

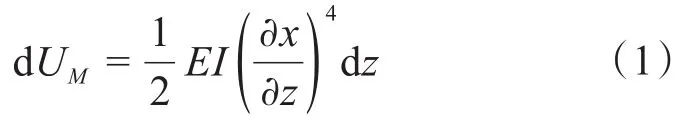
式中：EI为高压隔水管的抗弯刚度，Pa⋅m4。

在任意位置处由有效张力T引起的高压隔水管微元弯曲变形势能dUT可表示为：

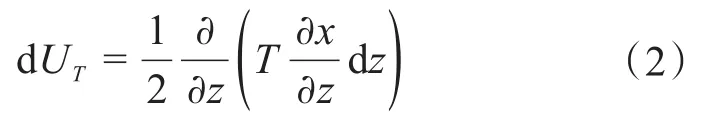
高压隔水管微元在波浪和海流作用下产生的动能为：

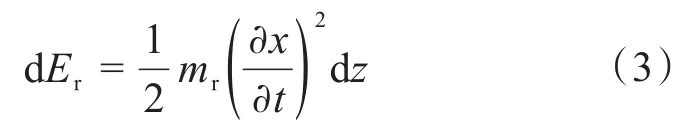
式中：mr为高压隔水管微元段质量，kg。

外载荷F（z，t）对高压隔水管微元做的功为［16］：

式中：C为海水的阻尼系数；ρw为海水密度，kg/m3；d1为高压隔水管外径，m；u为波浪水质点水平分速度（采用Stokes五阶波浪理论计算），m/s；CM为惯性力系数；vt为海面潮流速度，m/s；vw为海面风速，m/s；L为高压隔水管长度，m。

惯性力q对高压隔水管微元做的功为［17］：

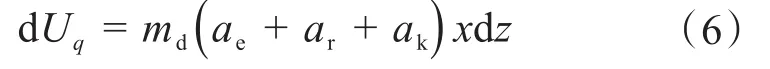
式中：md为单位长度高压隔水管内流体的质量，kg/m；ae为管内流体质点牵连加速度的切向分量，m/s2；ar为管内流体的相对加速度，m/s2；ak为管内流体的科式加速度，m/s2。

海水阻尼力对高压隔水管微元做的功为：

高压隔水管内部流体产生的动能为：

式中：mf为高压隔水管微元段流体质量，kg；v为高压隔水管内部流体速度，m/s。

综上所述，高压隔水管微元势能由外力做的功和动能组成，可表示为：

则高压隔水管在1个周期τ内的总能量为：

根据能量最低（稳态）原理，变形后∏满足欧拉方程，则可得高压隔水管的运动微分方程为：

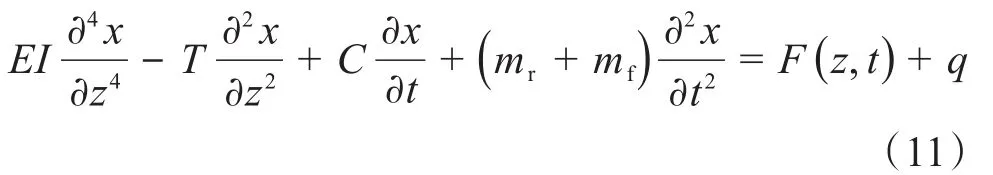
钻井作业时高压隔水管上端通过挠性接头与钻井平台连接，高压隔水管上端的横向运动可以用平台的横荡运动Sp（t）来描述，上挠性接头的旋转刚度为Ku，则上边界条件可表示为：

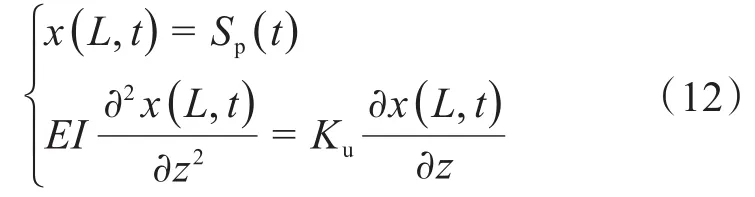
高压隔水管下端通过球铰与水下断开系统连接，下挠性接头的旋转刚度为Kb，则下边界条件可表示为：

2.2 张紧器受力分析

如图3所示，张紧器由液压缸、高压油气蓄能器及低压氮气压缩空气瓶组成。液压缸上端通过接口与平台连接，下端通过活塞杆与隔水管连接；液压缸活塞两端的压差形成张紧力。

将张紧器看作一个大型的气液弹簧，其活塞杆受力分析如图4所示。

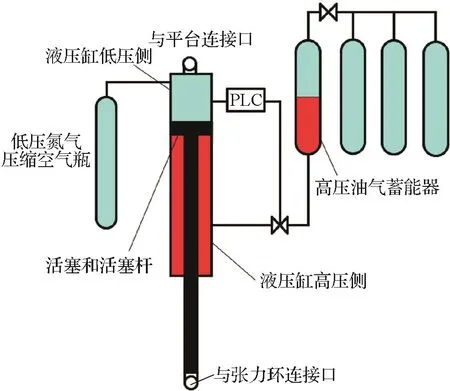
图3 张紧器结构示意图Fig.3 Diagram of tensioner structure

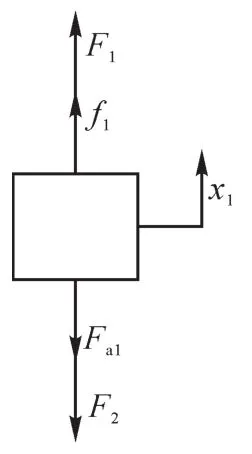
图4 张紧器活塞杆受力分析Fig.4 Force analysis of tensioner piston rod

张紧器-高压隔水管耦合动力学方程为：

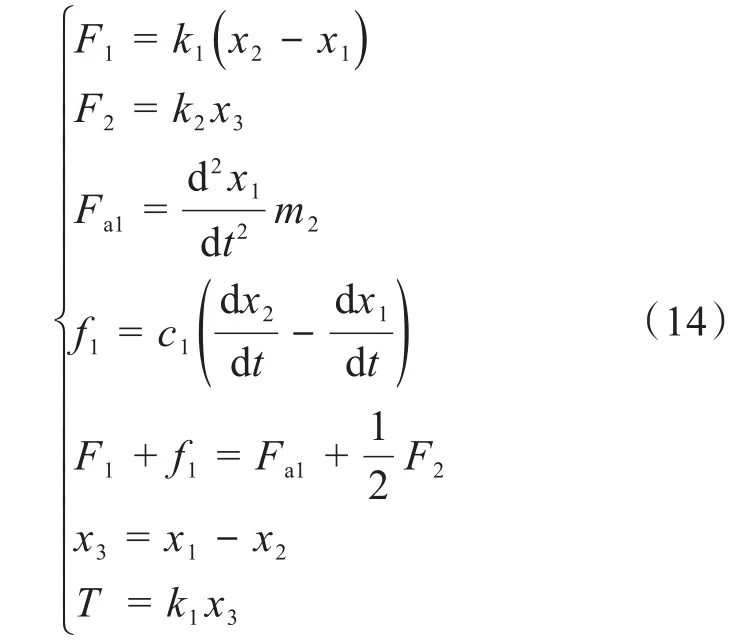
式中：F1为气液弹簧恢复力，N；k1为张紧器气液混合缸的刚度，N/m；x2为钻井平台升沉位移，m；x1为张紧器补偿缸活塞的位移，m；x3为张紧器与高压隔水管之间的应变位移，m；F2为张紧器活塞受到的隔水管的作用力，N；k2为隔水管等效刚度，N/m；Fa1为张紧器活塞和活塞杆等的惯性力，N；m2为张紧器活塞和活塞杆的质量，kg；f1为气液混合缸的阻尼力，N；c1为张紧器的阻尼系数，N/（m/s）。

对式（14）进行拉普拉斯变换并整理，可得张紧力与钻井平台位移之比：

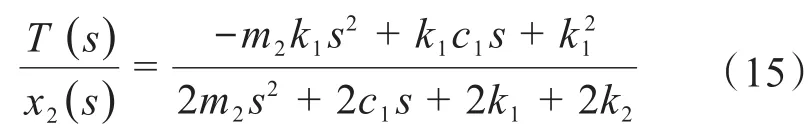
3 模型求解

3.1 高压隔水管横向振动模型求解

高压隔水管横向振动模型包含了对时间和空间的二阶偏导。在求解偏微分方程时，Runge-Kutta法和有限差分法应用最为广泛［18-19］，本文采用有限差分法。

根据上文假设，将高压隔水管沿长度方向划分为n段，得到n+1个节点，自下而上依次给节点i编号，i=1，2，3，…，n，n+1，每段隔水管的长度为h。设模型的计算时间为t，时间步长为Δt，离散时间得到k+1个时间节点，时间节点j=1，2，3，…，k，k+1，其中k表示某一时刻。由此可得高压隔水管第i个节点在k时刻的位移为x（i，k）。基于有限差分法，得到高压隔水管横向振动微分方程组的差分格式：

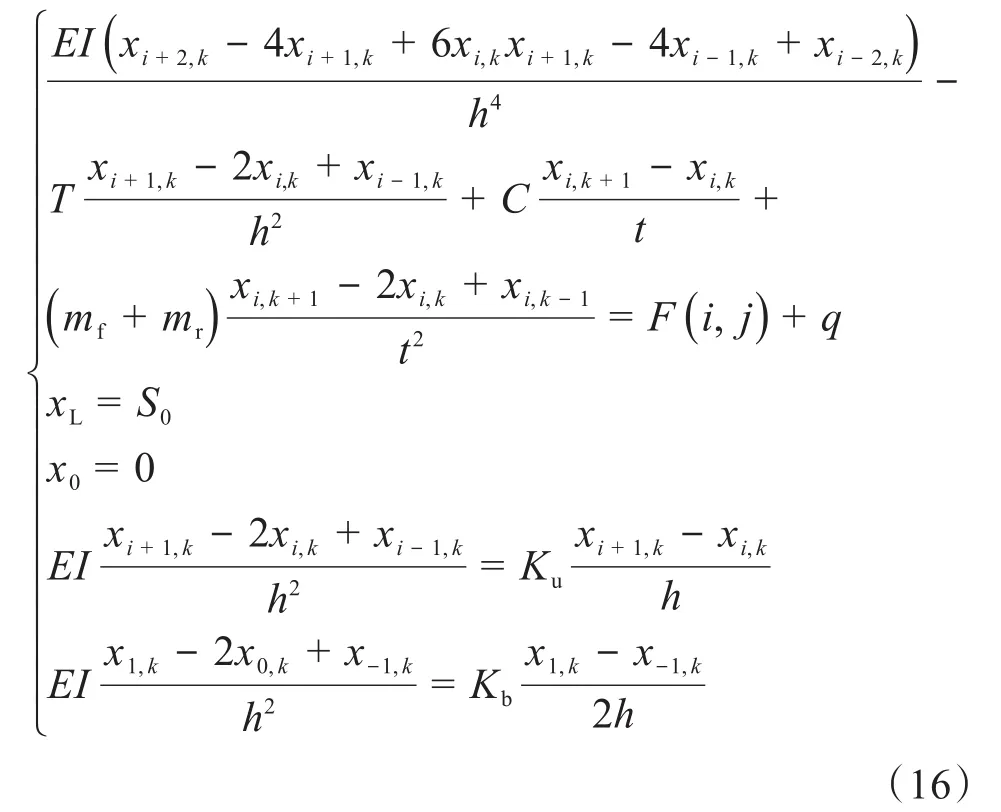
式中：xL为高压隔水管上边界，x0为高压隔水管下边界，S0为平台漂移距离，m。

差分方程组共有n-1个方程，加上边界条件后共有n+3个方程而构成线性方程组，则差分方程组共有n+3个未知量，在MATLAB/Simulink中利用MAT-LAB Function模块编程，对该封闭方程组进行求解。

3.2 张紧力模型求解

根据张紧力数学模型，在MATLAB/Simulink中搭建张紧力求解模型，如图5所示。

图5 张紧力求解模型Fig.5 Tension force solution model

3.3 耦合模型求解

将高压隔水管求解模型与张紧力求解模型耦合起来，在MATLAB/Simulink中搭建的张紧力-高压隔水管耦合动力学仿真模型如图6所示。

图6 张紧力-高压隔水管耦合动力学仿真模型Fig.6 Coupling dynamics simulation model of tension-high pressure riser

4 深水钻井仿真与结果分析

某井位作业环境的水深为1 900 m，海水密度为1 030 kg/m3，海流流速为1.07 m/s，潮流流速为0.5 m/s，海水阻力系数为0.45，海浪高度为8 m，波浪周期为20 s；钻井液密度为1 600 kg/m3；隔水管的弹性模量为210 GPa；张紧器单位体积压力为10 MPa。高压隔水管与常规隔水管的参数如表1所示，表中“HR”表示高压隔水管，“LR”表示常规隔水管。

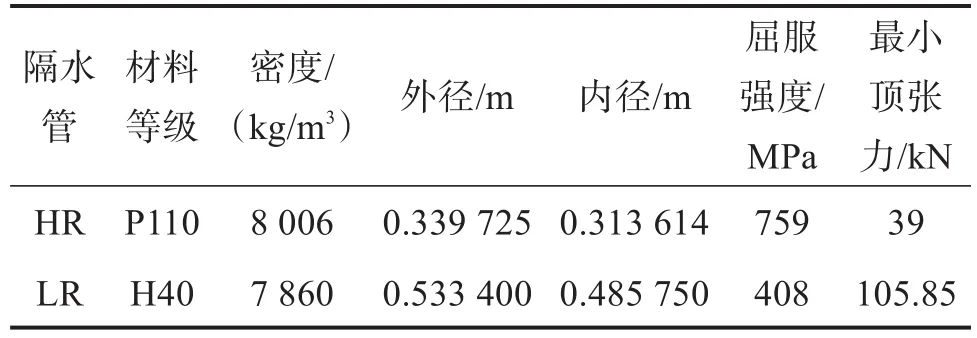
表1 高压隔水管与常规隔水管的参数Table 1 Parameters of high pressure riser and convention-al riser

本文通过仿真分析，讨论管内流体、张紧器耦合作用、海流流速、平台漂移量以及张紧器张力比等因素对高压隔水管横向振动的影响规律。

4.1 模型验证

采用商业软件OrcaFlex对钻井工况下高压隔水管的横向振动进行模拟计算与分析。在OrcaFlex软件中，将钻井平台简化为刚体模型，用线单元模型模拟隔水管，用弹簧阻尼模型模拟张紧器；隔水管顶部通过柔性节点与张紧器相连。在OrcaFlex中搭建的钻井平台-张紧器-高压隔水管耦合计算模型如图7所示，高压隔水管横向振动位移、张紧力仿真值与计算值对比如图8所示。

由图8可知，仿真值与计算值比较接近。由OrcaFlex软件仿真得到的与由本文方法计算得到的张紧力值之间的误差主要由模型简化引起。2条张紧力曲线拟合较好，整体误差在5%以内，证明本文建立的高压隔水管-张紧器的耦合模型是正确、可行的。

图7 钻井平台-张紧器-高压隔水管耦合计算模型Fig.7 Coupling calculation model of drilling platform-ten-sioner-high pressure riser

图8 高压隔水管横向振动位移、张紧力仿真与计算结果对比Fig.8 Comparison of simulation and calculation results of transverse vibration displacement and tension force of high pressure riser

4.2 管内高压流体的影响

对高压隔水管横向振动进行仿真分析，考虑管内高压流体时用“HF”表示，不考虑管内高压流体时用“HFN”表示，常规隔水管不需考虑内部流体的影响，结果如图9所示。

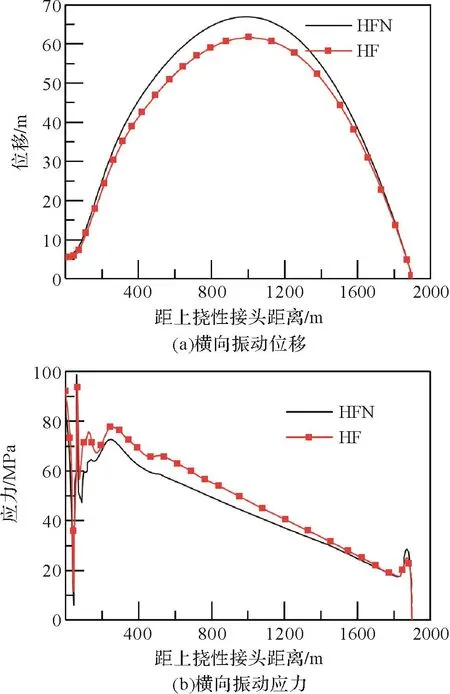
图9 内部高压流体对高压隔水管横向振动的影响Fig.9 Effect of internal high pressure fluid on transverse vi-bration of high pressure riser

由图9（a）可知：考虑内部高压流体时高压隔水管的最大横向位移为61.6 m，不考虑内部高压流体时高压隔水管的最大横向位移为70.1 m。由图9（b）可知：考虑内部高压流体时高压隔水管的横向振动应力比不考虑内部高压流体时大。出现上述结果的原因是，考虑内部高压流体相当于增大了高压隔水管的质量，导致其位移减小，应力增大。

4.3 张紧器耦合作用的影响

对高压隔水管和常规隔水管的横向振动进行仿真分析，考虑张紧器耦合作用时用“TC”表示，不考虑张紧器耦合作用时用“TCN”表示，结果如图10所示。

由图10（a）可知：考虑张紧器耦合作用时，高压隔水管的最大横向位移为64.7 m，常规隔水管的最大横向位移为38.6 m；不考虑张紧器耦合作用时，高压隔水管的最大横向位移为69.3 m，常规隔水管的最大横向位移为43.7 m。由此可得张紧器耦合下隔水管的横向位移比未耦合时的横向位移小，说明张紧器耦合下隔水管抵抗变形的能力增强。由图10（b）可知：考虑张紧器耦合作用时隔水管的横向振动应力大于不考虑张紧器耦合作用时。说明张紧器的耦合作用使隔水管的横向位移减小、应力增大。在实际应用中，张紧力是在一定范围内波动的，说明考虑张紧器耦合作用更贴近实际工况。

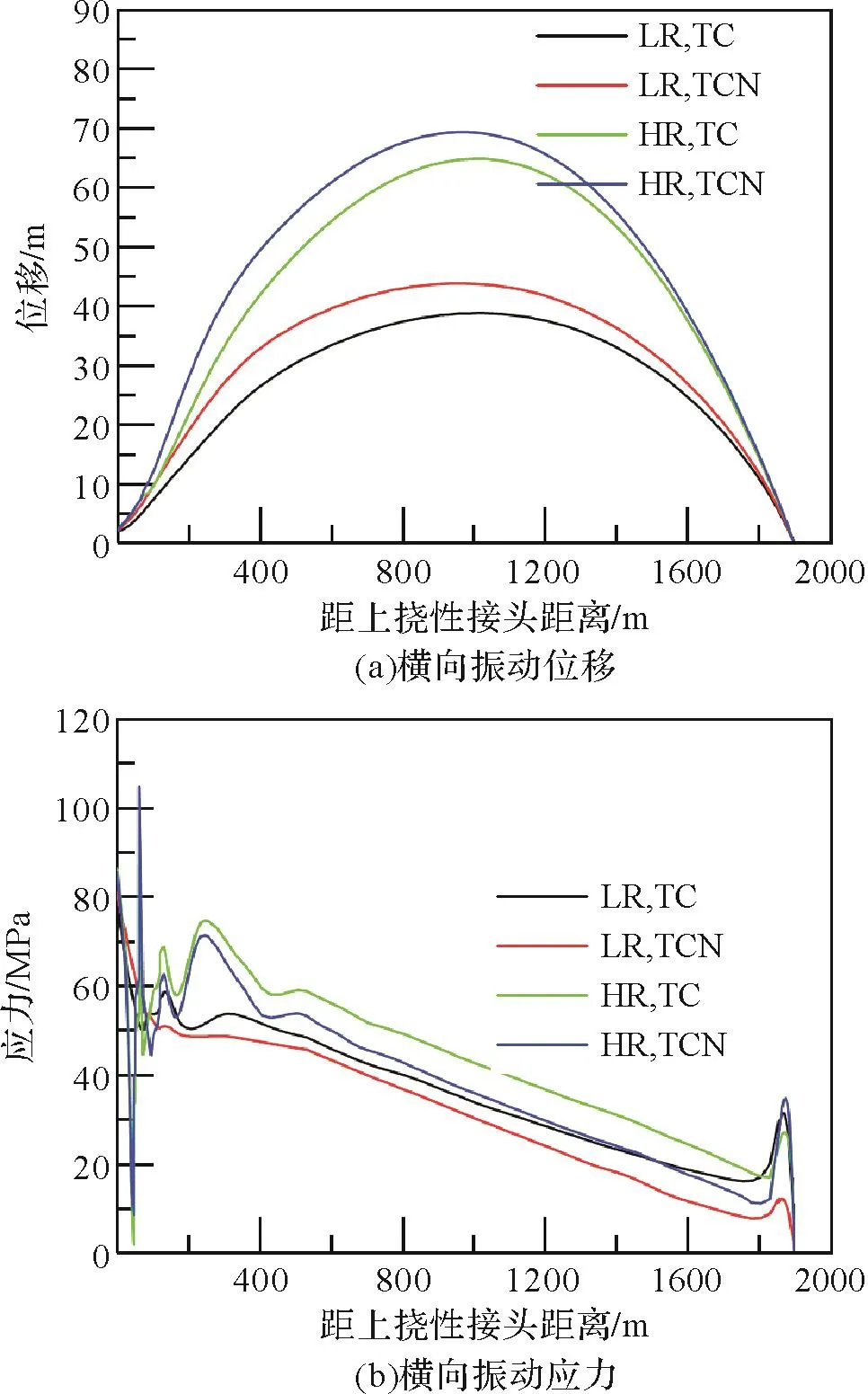
图10 张紧器耦合作用对隔水管横向振动的影响Fig.10 Effect of tensioner coupling on transverse vibration of riser

4.4 海流流速的影响

取海流流速vc=0.87，1.07，1.27 m/s，对高压隔水管和常规隔水管的横向振动进行仿真分析，结果如图11所示。

由图11（a）可知：随着海流流速的增大，隔水管的横向振动位移增大；在海流流速为1.27 m/s时，高压隔水管最大横向位移为66.5 m，常规隔水管的最大横向振动位移为41.8 m。由此可知高压隔水管的横向振动位移明显大于常规隔水管，这是因为常规隔水管的管径、质量及刚度均大于高压隔水管，在海流作用下其横向振动位移变化较小。由图11（b）可知：隔水管底部的横向振动应力基本不随海流流速而变化，而位于海面附近的隔水管的横向振动应力随海流流速的增大而增大，说明海流速度只对海面附近的隔水管有影响。

4.5 平台漂移量的影响

取平台漂移量f=0，5，10 m，对高压隔水管和常规隔水管的横向振动进行仿真分析，结果如图12所示。

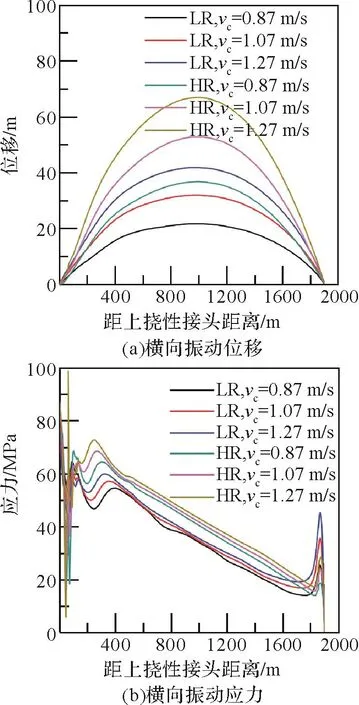
图11 海流流速对隔水管横向振动的影响Fig.11 Effect of sea current velocity on transverse vibration of riser

图12 平台漂移量对隔水管横向振动的影响Fig.12 Effect of platform drift on transverse vibration of riser

由图12（a）可知：随着平台漂移量的增大，高压隔水管和常规隔水管的最大横向位移增大，且隔水管上部的横向位移变化越明显，这是因为隔水管底部固定，受平台漂移量的影响较小。由图12（b）可知：随着平台漂移量的增大，隔水管的横向振动应力变化不明显，高压隔水管的横向振动应力大于常规隔水管。

4.6 张紧器张力比的影响

张紧器提供的张紧力与高压隔水管重量的比值称为张紧器的张力比。调节张紧器参数，取张紧器的张力比e=0.9，1，1.1，对高压隔水管和常规隔水管的横向振动进行仿真分析，结果如图13所示。

图13 张紧器张力比对隔水管横向振动的影响Fig.13 Effect of tension ratio of tensioner on transverse vi-bration of riser

由图13（a）可知：当张紧器张力比为0.9时，高压隔水管的最大横向位移为118.6 m，常规隔水管的最大横向位移为58.1 m；随着张紧器张力比增大，隔水管横向位移减小，这是因为张力比增大相当于增大了隔水管的弯曲刚度，使得隔水管抵抗变形的能力增强。由图13（b）可知：随着张紧器张力比增大，隔水管的横向振动应力逐渐增大。对于常规隔水管，由于其底部质量过大，张紧力不足易导致应力集中，因此在保证隔水管安全的前提下应适当增大张力比，防止隔水管出现较大的变形。

5 结 论

1）基于动力学基本原理建立了张紧器-高压隔水管耦合横向振动力学模型，并采用有限差分法进行离散求解。

2）在钻井工况下，高压隔水管和常规隔水管在相关参数激励下，其动力学特性表现出相同的变化趋势，但高压隔水管的横向振动位移和应力均大于常规隔水管；在管内高压流体、张紧器耦合作用的影响下，高压隔水管的横向振动位移减小、应力增大；隔水管横向振动位移随海流流速、平台漂移量的增大而增大，随张紧器张力比的增大而减小；隔水管横向振动应力随海流流速、张紧器张力比的增大而增大。