基于柔性腕手的最优抓取规划研究

张 潇，张秋菊

（1.江南大学机械工程学院，江苏无锡214122；2.江苏省食品先进制造装备技术重点实验室，江苏无锡214122）

随着自动化产业的快速发展，机械手和机械臂被广泛应用于工业领域。由于传统工业机器人的末端夹持器难以实现和满足多样化的抓取需求，国内外学者在机器人多指手方面进行了大量研究，并取得了一些成果，例如：美国麻省理工学院和犹他大学联合研制的UTAH/MIT手［1］以及日本岐阜大学研制的Gi-fu-2手［2］等仿人手的机器人多指手；美国Barrett科技公司设计的Barrett灵巧手［3-5］以及美国哈佛大学和耶鲁大学于2014年联合研制的iRobot-Harvard-Yale（iHY）灵巧手［6］等可以改变构型的多指手，其适用于工业自动化领域；北京航空航天大学研制的BUAA灵巧手［7］和哈尔滨工业大学研制的HIT灵巧手［8］等。为了提高多指手的柔顺性，国内外学者开始尝试采用新型材料制作手指，如英国Shadow公司利用气动肌肉研制的可弯曲的Shadow灵巧手［9］、浙江工业大学利用新型气动柔性驱动器（flexible pneumatic actua-tor，FPA）关节研制的ZJUT气动柔性机械手［10］以及北京航空航天大学研制的通用气动软体机械手［11］等，这类手指具有柔顺性，比较适用于抓取软、脆、易损的物体。

在抓取物体之前，必须对多指手进行抓取规划，即根据实际任务确定接触模型，以合理确定接触点的个数和位置［12］。Lin等［13］提出了一种基于人手抓取策略的抓取方法，考虑了抓取对象的类型和拇指的位置与方向等因素；Ko等［14］提出了一种基于最优抓取力的抓取规划方案；Zheng等［15］以接触力最佳为优化目标，提出了一种在摩擦系数不确定的情况下计算所需最小摩擦系数的智能算法；Mavrogiannis等［16］提出了一种新的抓取力优化方法。国内的一些学者也对多指手的抓取规划方法进行了研究［17-21］，如：杨洋［18］根据软手指接触模型，提出了一种基于广义力椭球的最优抓取规划方法；大连理工大学的Xu等［21］基于Barrett灵巧手提出了一种抓取规划算法。但是，上述抓取规划方法在实际应用中都存在一定的局限性，且计算过程较为复杂，需进一步改善。

针对食品自动化加工行业，为实现对软、脆、易损，尺寸、形状差异较大的物体的稳定抓取，笔者设计了一款柔性腕手，并对其抓取规划进行分析，提出了一种适用于该柔性腕手的最优抓取规划算法，以获得物体在实际工作环境中的最优抓取点。柔性腕手可通过构型变换，基于最优抓取点对不同物体进行抓取，以提高抓取的稳定性与效率。

1 柔性腕手的设计

在食品自动化加工行业中，对于柔、脆、易损，尺寸、形状差异较大的物体，传统机器人的末端夹持器难以实现较好的抓取［22］。针对上述抓取难题，笔者研制了如图1所示的软体手指［23］。该软体手指由硅橡胶制作而成，具有一定的柔性，可以根据气压的大小改变弯曲度，从而改变夹持力，实现软、脆、易损物体的抓取。

图1 软体手指实物图Fig.1 Physical picture of soft finger

针对尺寸、形状差异较大的物体，笔者已设计了一种仿人手掌的机器人变掌机构［24］。结合软体手指和变掌机构，设计了柔性腕手，其结构如图2所示。其中，变掌机构的手臂2，4可绕机构中心旋转30°～150°，可带动软体手指以改变抓取点的位置，从而实现形状差异较大的物体的抓取；同时，变掌机构有4个移动副，软体手指在移动副的带动下可在变掌机构的手臂1，2，3，4上移动，以扩大工作空间，从而实现尺寸差异较大的物体的抓取。

柔性腕手共有6个自由度，在实际应用中，柔性腕手可通过构型变换来抓取不同物体。在已知物体的抓取点个数以及抓取点位置坐标时，柔性腕手的构型变换参见文献［24］，本文不再赘述。下面将对柔性腕手的最优抓取规划进行深入分析。

图2 柔性腕手结构示意图Fig.2 Structure diagram of flexible wrist-hand

2 柔性腕手的最优抓取规划分析

本文所设计的柔性腕手主要用于食品自动化加工行业，其抓取对象比较特殊。因此，下文将针对不同抓取需求，对柔性腕手的最优抓取规划进行分析。

2.1 实际抓取需求分析

在食品自动化加工行业中，大量抓取对象柔软，易损，如鸡蛋、饼干、面包等，因此在抓取过程中必须保证抓取的稳定性和柔顺性。此外，在抓取任务中，若物体的摆放位置过近，导致其间距小于软体手指的宽度，则可能存在无法抓取的边界部分，如图3所示，此时需要调整抓取点的个数和位置，以对其余边界进行抓取。

图3 摆放过近的柠檬的不可抓取边界Fig.3 Ungraspable boundary of lemons placed too close

2.2 抓取稳定性评价方法分析

当抓取满足力封闭时，Ferrari等［25］定义了2个抓取稳定性评价指标，其中应用较为广泛的是力螺旋空间中原点到由原始力螺旋矩阵构成的凸包多面体的最小距离，采用该指标的评价方法被称为最大内切球准则［26］。使用最大内切球准则评价抓取稳定性的前提是［27］：1）给定静摩擦系数，计算凸包多面体每一个面与力螺旋空间中原点的距离，从而求出最小内切球半径，即稳定性评价指标值；2）所有接触点的法向力归一化处理后的和为1。

柔性腕手所抓取物体的形状、尺寸各异，在实际应用中很难根据摄像头所采集的信息来获取物体表面与软体手指之间的静摩擦系数；同时，软体手指由柔性材料制成，具有自适应性，不需要非常精确地计算手指与物体之间的接触力。因此，上述最大内切球准则并不适用于柔性腕手的稳定性评价。下面将从实际工业应用出发，对柔性腕手的抓取稳定性评价指标进行分析。

2.2.1 利用四指抓取物体时的稳定性评价指标

柔性腕手具有一定的柔顺性，在抓取物体时其手指具有一定的自适应性。因此，当柔性腕手利用四指抓取物体时，考虑根据手指对物体施加的力与接触点切面法线的夹角大小来评价其抓取稳定性［28］。

图4所示为利用四指抓取物体时柔性腕手的构型示意图，其中，F1、F2、F3和F4表示柔性腕手的4条手臂，fi（i=1，2，3，4）为4根手指对物体施加的力，α为手臂F2可旋转的角度，β为手臂F4可旋转的角度，φi为fi与接触点切面法线的夹角。

图4 利用四指抓取物体时柔性腕手的构型示意图Fig.4 Configuration diagram of flexible wrist-hand when grasping object with four fingers

在利用四指抓取物体时，如果其中1根手指的接触失效了，那么柔性腕手的抓取稳定性就会大幅下降，因此应尽可能让每个φi的值最小。定义利用四指抓取物体时柔性腕手的稳定性评价指标为：

Q4值越小表明柔性腕手4根手指对物体施加的力与接触点切面法线的夹角越小，则手指与物体表面的接触效果越好。

2.2.2 利用三指抓取物体时的稳定性评价指标

利用三指抓取物体时柔性腕手的构型示意图如图5所示，其中，θ1和θ2为相邻2个抓取点与物体质心连线所形成的夹角。此时，若采用式（1）评价柔性腕手的稳定性，由于φ1、φ3和φ4均很小，则计算得到的评价指标Q4也很小，即柔性腕手手指与物体的接触效果较好。但从图5中可明显看出，此时柔性腕手的抓取效果并不好，这是因为物体的质心Oo位于柔性腕手的工作空间之外，3个抓取点分布不均匀，从而导致抓取不稳定。

图5 利用三指抓取物体时柔性腕手的构型示意图Fig.5 Configuration diagram of flexible wrist-hand when grasping object with three fingers

在食品自动化加工行业中，大部分被抓取物体的密度都较均匀。因此，假设所抓取的物体为实体且密度均匀，即物体的质心与形心重合。当柔性腕手手指与物体表面的接触效果较好时，柔性腕手的中心离物体的质心Oo越近，则抓取点分布越均匀，即抓取越稳定，令：

Q3H值越小表明相邻2个抓取点与物体质心连线所形成的夹角越接近120°，即抓取点分布越均匀。

根据手指对物体施加的力与接触点切面法线的夹角，令：

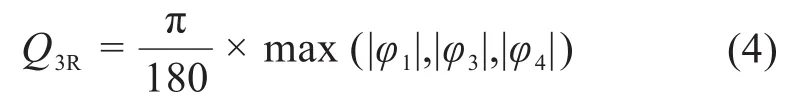
通过Q3R的值能判断柔性腕手手指与物体表面的接触效果是否良好，Q3R值越小表明接触效果越好。

综合考虑以上2种因素，引入权重系数KH和KR，定义利用三指抓取物体时柔性腕手的稳定性评价指标为：

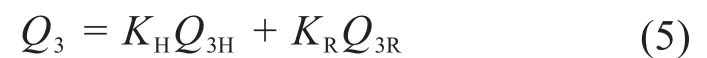
式（5）中KH+KR=1，KH与KR的值可以根据被抓取物体来定义：若被抓取物体的边界较为复杂，则令KR较大，使手指更好地与物体表面接触；若物体的质量较大，边界比较简单，则令KH较大，使抓取点分布更均匀，即柔性腕手中心与物体质心更近。Q3值越小表明利用三指抓取物体时柔性腕手的稳定性越好。

2.2.3 利用二指抓取物体时的稳定性评价指标

利用二指抓取物体时柔性腕手的构型示意图如图6所示，此时抓取物体使用的是柔性腕手的手臂F1和F3。其中，λ为抓取点a、b与质心连线的夹角。

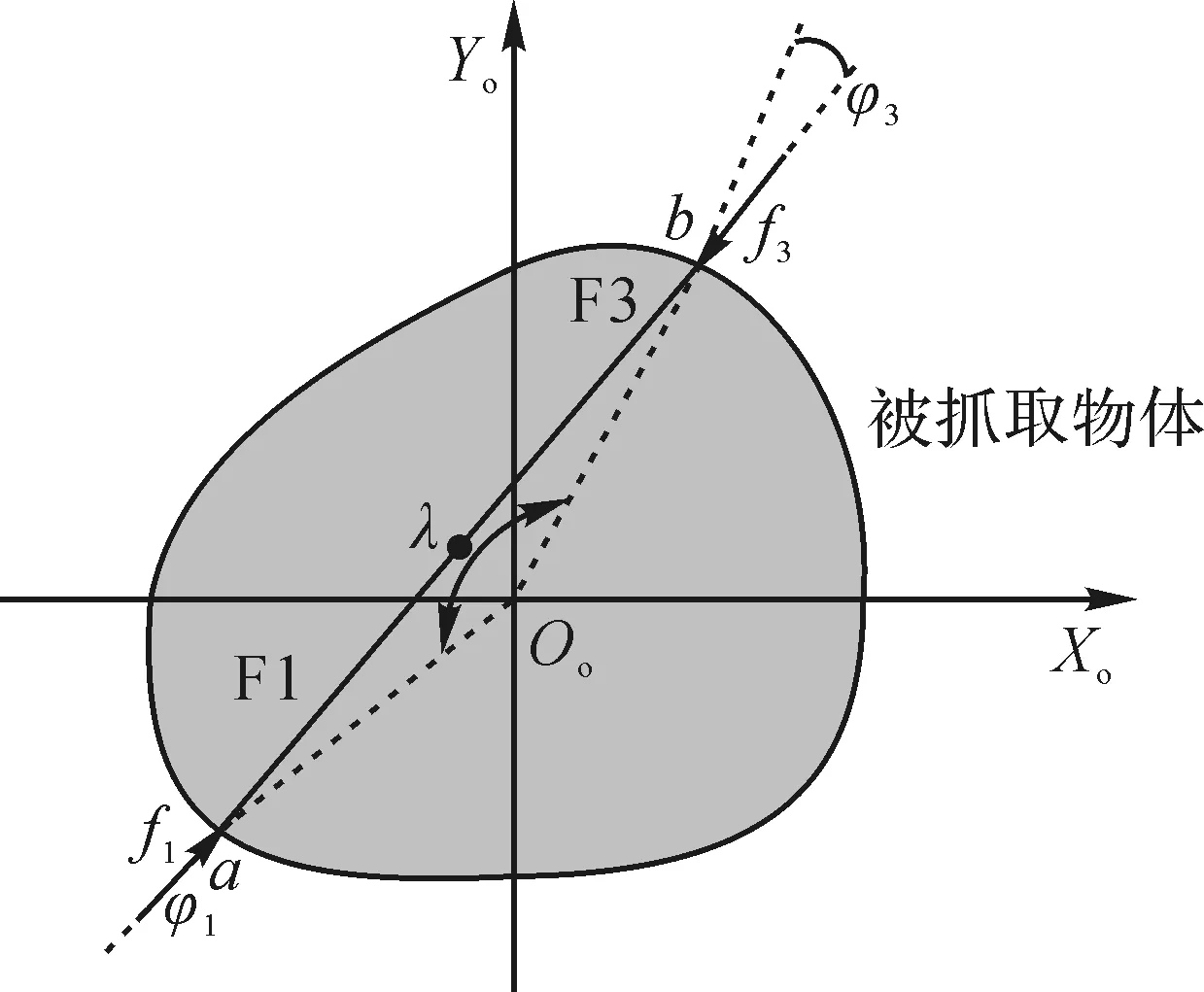
图6 利用二指抓取物体时柔性腕手的构型示意图Fig.6 Configuration diagram of flexible wrist-hand when grasping object with two fingers

同理，利用二指抓取物体时同样需要考虑抓取点的分布情况以及柔性腕手手指与物体表面的接触效果，令：

Q2H值越小表明2个抓取点所连成的直线与物体质心的距离越小，则物体质心与柔性腕手中心越近，即抓取点分布越均匀。Q2R值越小表明柔性腕手手指与物体表面接触效果越好。

另外，如图7所示，在利用二指抓取物体时，将点C和点D作为抓取点时，Q2H和Q2R取得最小值，但将点A和点B作为抓取点时，柔性腕手的稳定性更好，令：

式中：lz为2个抓取点之间的距离。

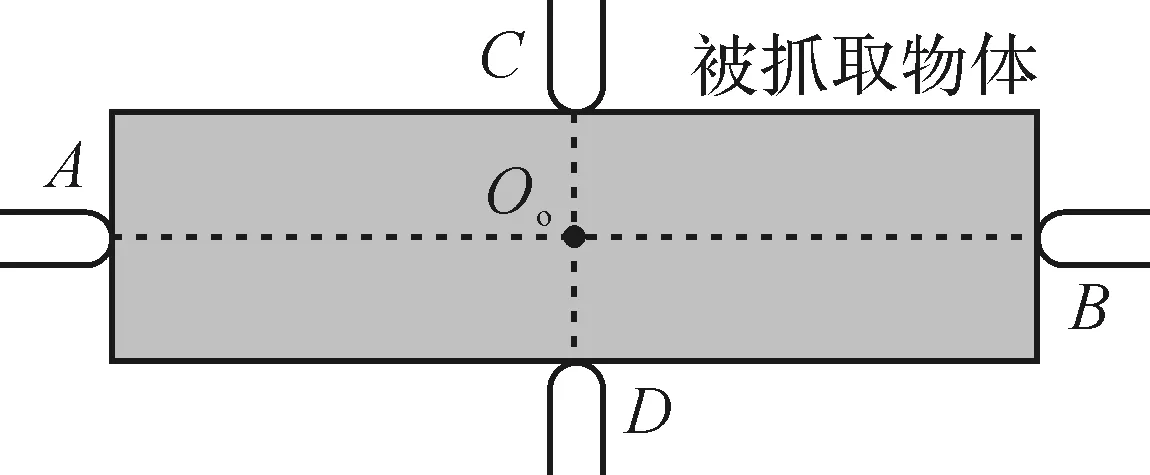
图7 利用二指抓取长方形物体时柔性腕手的稳定性分析Fig.7 Stability analysis of flexible wrist-hand when grasping a rectangular object with two fingers

综合上述3种因素，并引入权重系数KL，定义利用二指抓取物体时柔性腕手的稳定性评价指标为：

式（9）中KH+KR+KL=1。若被抓取的物体为扁长形，则可令KL的值较大。Q2值越小表明利用二指抓取物体时柔性腕手的稳定性越好。

2.3 最优抓取规划算法

基于上述柔性腕手的稳定性评价指标，提出一种适用于柔性腕手的最优抓取规划算法，其具体步骤为：

1）对所载入的物体图像进行处理，得出所抓取物体及其周围物体的边界。

2）找到物体的质心，以4°为间距角作射线，得到与边界相交的90个边界点。

3）以物体质心为中心，将90个边界点向外偏置20 mm（软体手指的工作厚度）。若偏置后的边界点与其他物体重合，则视其为无效点，若2个无效点之间的距离小于30 mm（软体手指的工作宽度），则这2个无效点之间的有效点也为无效点；反之均为有效点。

4）取4个有效点为一组，判断柔性腕手利用四指抓取物体是否可行：若不可行，则执行步骤5）；若可行，则计算稳定性评价指标Q4，并遍历所有有效点，比较得出使Q4最小的4个边界点，即最优抓取点。

5）取3个有效点为一组，判断柔性腕手利用三指抓取物体是否可行：若不可行，则执行步骤6）；若可行，则计算稳定性评价指标Q3，并遍历所有有效点，比较得出使Q3最小的3个边界点，即最优抓取点。

6）取2个有效点为一组，判断柔性腕手利用二指抓取物体是否可行：若不可行，则结束；若可行，则计算稳定性评价指标Q2，并遍历所有有效点，比较得出使Q2最小的2个边界点，即最优抓取点。

3 基于最优抓取规划算法的柔性腕手抓取实例计算

根据上文分析，通过抓取实例计算来验证基于柔性腕手的最优抓取规划算法的可行性。

1）图像预处理。首先，利用图像处理技术对所抓取物体及其周围物体的图像进行边缘处理，得到各物体的边界，如图8所示。

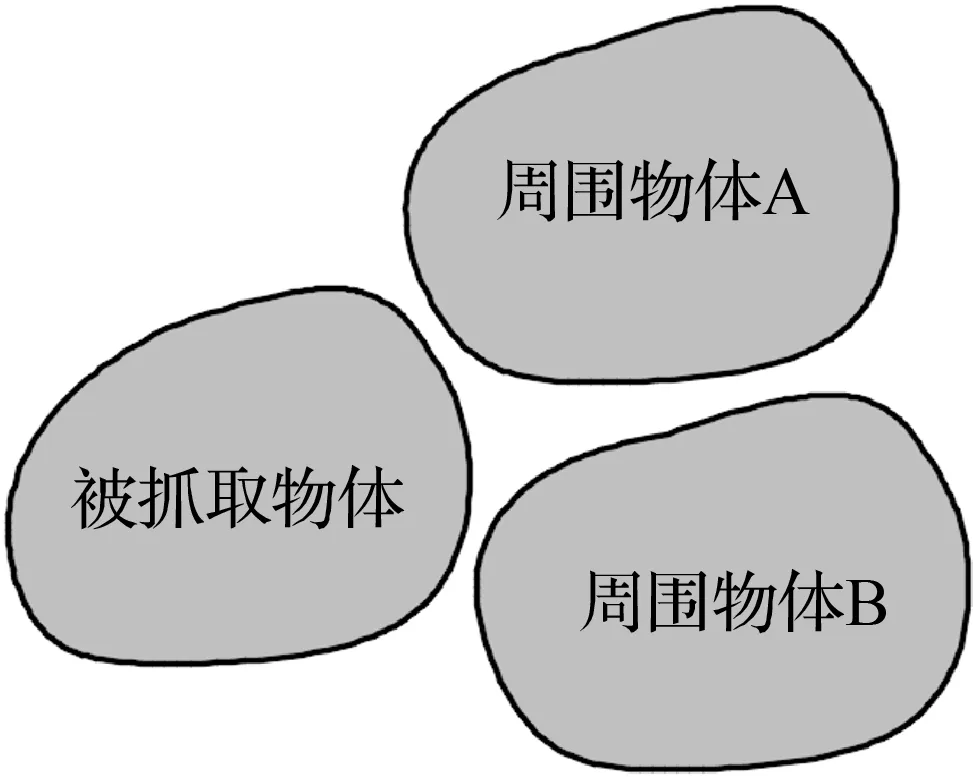
图8 物体边界示意图Fig.8 Schematic diagram of object boundary

2）划分边界。以被抓取物体的质心为中心，4°为间距角（可根据实际情况设置间距角的大小）作射线，得到与物体边界相交的90个边界点，如图9所示。

3）筛选有效点。将物体的边界点向外偏置20mm，可得被抓取物体的有效点与无效点，如图10所示。

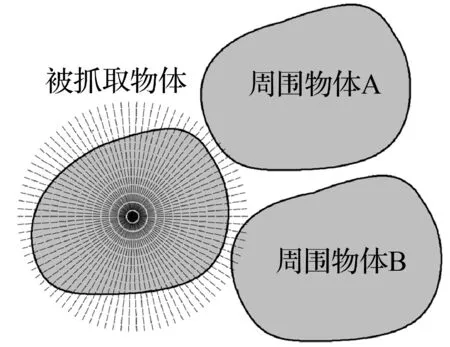
图9 被抓取物体边界划分示意图Fig.9 Schematic diagram of boundary division of grasped object

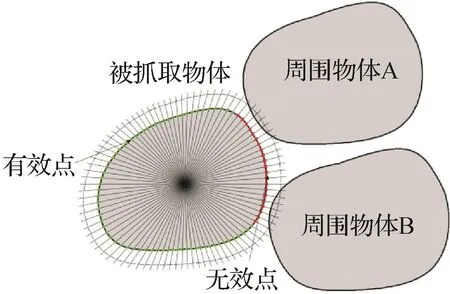
图10 被抓取物体的有效点与无效点示意图Fig.10 Schematic diagram of effective points and ineffective points of grasped object

4）判断柔性腕手的可行性。根据柔性腕手的机械结构可得其约束条件为：

式中：l为柔性腕手每个手臂的伸长量，即抓取点到柔性腕手中心的距离。

如图11所示，取a、b、c、d四个有效点为一组，以被抓取物体质心为原点建立坐标系，可得4个抓取点的坐标分别为：a（7.01，-66.65），b（-62.53，39.07），c（18.93，75.91），d（65.02，-47.23）。通过计算可得4个抓取点到柔性腕手中心的距离分别为：la=lc=71.53 mm，lb=82.98 mm，ld=73.43 mm，α=70°，β=110°，均满足式（10）的约束条件，因此可判定该柔性腕手利用四指抓取物体可行。

图11 柔性腕手可行性判定时有效点的选取示意图Fig.11 Schematic diagram of selection of effective points in the feasibility judgment of flexible wrist-hand

5）计算稳定性评价指标。根据上文利用四指抓取物体时的稳定性评价指标计算方法，利用梯度函数gradient求出过a、b、c、d四个点的切面的法线，然后将手臂F1、F2、F3和F4向外延长，求得fi与接触点切面法线的夹角φi为：

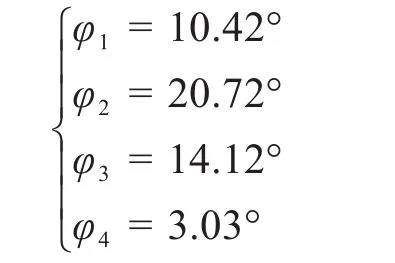
将各φi的值代入式（1），求得Q4-abcd=0.362。

6）求解稳定性评价指标最小值。另外选取4个有效点，重复步骤4）和5），直至遍历所有点。求解得到使Q4最小的4个有效点，即最优抓取点。通过大量的计算与比较，得出该物体的最优抓取点如图12所示，4个抓取点的坐标分别为：m（11.66，-66.15），n（-87.24，31.75），u（-11.97，67.89），v（49.52，73.42），此时φi（i=1，2，3，4）依次为7.43°，3.25°，7.65°，8.15°，将其代入式（1）求得稳定性评价指标Q4-mnuv=0.142＜Q4-abcd。

图12 被抓取物体的最优抓取点示意图Fig.12 Schematic diagram of optimal grasping points of grasped object

4 柔性腕手抓取实验

图13所示为柔性腕手抓取实验平台，该平台主要由工业机器人、柔性腕手和控制系统等组成，其中控制系统包括气路控制与运动控制两部分。此外，该实验平台还包括上位机、空气压缩机及过滤器等。

鉴于所设计的柔性腕手主要用于食品自动化加工行业，选取的抓取对象主要为各类食品。此外，为了验证柔性腕手的自适应性，主要挑选软、脆、易损以及尺寸、形状差异较大的物体进行抓取。抓取实验中所选物体的具体参数如表1所示。

图13 柔性腕手抓取实验平台Fig.13 Grasping experiment platform of flexible wrist-hand

表1 抓取实验中所选物体的具体参数Table 1 Specific parameters of selected objects in the grasping experiment

4.1 柔性腕手构型变换实验

如图14（a）所示，通过增大柔性腕手移动副的伸缩长度来扩大其工作空间，从而抓取尺寸大的物体；如图14（b）所示，通过改变柔性腕手2个旋转副的角度来调整抓取点的位置，从而抓取形状不同的物体。

图14 柔性腕手构型变换仰视图Fig.14 Upward view of configuration transformation of flexi-ble wrist-hand

对于某些物体，柔性腕手可以利用不同个数的手指以及不同构型进行抓取。图15所示为柔性腕手分别利用二指、三指和四指抓取袋装食品。

4.2 最优抓取规划算法的可行性验证实验

通过鸡蛋抓取实验来进一步验证所提出的最优抓取规划算法的可行性。根据上述最优抓取规划算法的前4个步骤确定了被抓鸡蛋的无效点与有效点，以及被抓鸡蛋仅可使用二指进行抓取。

首先，利用MATLAB软件的regionprops函数找到被抓鸡蛋的质心，并以鸡蛋的质心为原点建立坐标系XoOoYo，如图16所示。

图15 柔性腕手利用二指、三指、四指抓取袋装食品的实验现场Fig.15 Experimentsite offlexible wrist-hand grasping bagged food with two,three and four fingers

图16 鸡蛋的最优抓取点选取示意图Fig.16 Schematic diagram of optimal grasping point selec-tion for egg

其次，以2个有效点为一组，计算稳定性评价指标。如先选取u（-20.89，17.67）和v（13.05，-22.45）两点，设定式（9）中各权重系数分别为：KH=0.4，KR=0.3，KL=0.3。根据上述2个点的坐标计算得到λ=160.4°。利用梯度函数gradient计算得到过点u、v的切面的法线，从而计算得到：φ1=23.18°，φ3=7.88°。将λ、φ1、φ3等代入式（6）至式（8）可得：Q2H=0.342，Q2R=0.404，Q2L=0.019。将Q2H、Q2R、Q2L的值代入式（9）得到柔性腕手利用u、v两点抓取鸡蛋时的稳定性评价指标Q2-uv=0.2637。

最后，通过MATLAB软件遍历所有有效点，计算得出所有可能的稳定性评价指标并进行比较，取最小值以确定最优抓取点。最终得到的最优抓取点为图16所示的点m、n，计算过程中的具体参数如下：

熊有伦等［29］的研究表明类似鸡蛋的椭圆形物体的最优抓取点也位于m、n点附近，这证明了本文提出的最优抓取规划算法可行。图17所示为柔性腕手基于最优抓取规划算法抓取鸡蛋的实验现场。

图17 柔性腕手基于最优抓取规划算法抓取鸡蛋的实验现场Fig.17 Experiment site of flexible wrist-hand grasping eggs based on optimal grasping planning algorithm

4.3 柔性腕手对多种物体的抓取实验

图18所示为柔性腕手抓取灌装食品的实验现场。灌装食品的不同摆放位置如图18（a）、（e）所示，利用最优抓取规划算法分析位于中间的灌装食品的最优抓取点；根据最优抓取点，柔性腕手进行构型变换，如图18（b）、（f）所示；根据最优抓取点的坐标，工业机器人控制柔性腕手进行抓取，其中图18（c）、（d）为柔性腕手利用二指抓取灌装食品，图18（g）、（h）为柔性腕手利用三指抓取灌装食品。

图18 柔性腕手抓取灌装食品的实验现场Fig.18 Experimentsite offlexible wrist-hand grasping canned food

图19所示为柔性腕手抓取易损食品的实验现场。选取的实验对象为表面比较光滑的苹果以及表面粗糙的土豆，这2种食品的表面都易破损。图19（b）、（c）所示分别为柔性腕手利用三指、四指抓取图19（a）所示的位于中间和外侧的苹果。图19（e）、（g）所示分别为柔性腕手利用四指、三指抓取图19（d）、（f）所示的位于中间的土豆。

图19 柔性腕手抓取易损食品的实验现场Fig.19 Experiment site of flexible wrist-hand grasping vul-nerable food

图20所示为柔性腕手抓取袋装面包和盒装饼干的实验现场。袋装面包较软，而盒装饼干易碎，因此在抓取时不能有较大的变形。图20（b）所示为柔性手腕利用二指抓取图20（a）所示的位于外侧的袋装面包（方形），图20（d）、（e）所示分别为柔性手腕利用四指、三指对抓取图20（c）所示的位于中间的袋装面包（圆形）。图20（g）、（i）所示为柔性手腕利用四指抓取图20（f）、（h）所示的位于右侧和中间位置的盒装饼干。

实验结果表明：柔性腕手可以抓取软、脆、易损，尺寸、形状差异较大的物体，具有较强的自适应性；同时，利用本文提出的最优抓取规划算法可以准确计算出物体的最优抓取位置，使得柔性腕手更稳定地抓取物体。

图20 柔性腕手抓取袋装面包和盒装饼干的实验现场Fig.20 Experimentsite offlexible wrist-hand grasping bagged bread and boxed biscuits

5 结论

利用软体手指和变掌机构，研发了一款柔性腕手，该柔性腕手可以通过构型变换来实现各种软、脆、易损，尺寸、形状差异较大物体的抓取。基于实际抓取需求分析，确定了柔性腕手利用四指、三指、二指抓取物体时的稳定性评价指标计算方法，并提出了基于柔性腕手的最优抓取规划算法。选取了8种不同的物体，在实验平台上展示了柔性腕手的构型变换；通过鸡蛋抓取实验验证了最优抓取规划算法的可行性，同时对多种物体进行了抓取实验。实验结果表明，该柔性腕手可灵活抓取软、脆、易损，尺寸、形状差异较大等物体，且最优抓取规划算法可准确计算最优抓取点，适用于实际抓取任务。研究结果为机器人多指手的应用提供了重要参考。