工作索耦合作用下多档多载荷货运索道的分析与计算方法

张卫东，秦 剑，陈 迪，李其莹，乔 良，孙国磊

（1.国网山东省电力公司，山东济南250001；2.中国电力科学研究院有限公司，北京100055；3.中国合格评定国家认可中心，北京100062）

架空货运索道具有对山区地形适应性好、载荷运输能力强、对环境破坏小等优点，是山地施工中常用的运输工具［1-2］，被广泛应用于林业、矿山、电力、建筑等多个行业。

货运索道的主要承力部件有工作索、支架（含横梁和支腿等）、载货小车、转向滑车和地锚。工作索包括承载索和牵引索，其中：承载索承担索道的运输荷重；牵引索与支架、转向滑车形成闭合的运行系统，牵引载货小车沿承载索移动［3］。

在设计货运索道时，需重点关注承载索和牵引索的运行张力及索形的变化。目前悬索结构的分析与计算方法主要包括有限元法［4-7］、解析计算法［8-12］等，多用于悬索桥、输电线等结构的分析与计算。另外，很多学者针对悬索附有固定质量时的动力学问题展开了研究，提出了弹性悬索的自由振动计算方法［13-14］，以及具有移动集中载荷的柔性索的动力学计算方法［15-16］等。

但是，目前对货运索道的研究仍限于对承载索及载荷系统的分析，未考虑牵引索与载荷之间的作用关系，导致在载荷移动过程中承载索张力的计算结果与实际有较大差别。同样，由于未考虑牵引索与承载索之间的作用关系，目前仍未有合理的计算方法来分析牵引索的张力，导致牵引索的安全系数取值缺乏理论依据。

为解决上述问题，笔者基于弹性悬索的悬链线方程提出了一种适用于承载任意载荷的多档货运索道在工作索耦合作用下分段悬链线的分析与计算方法，旨在为多档货运索道的载荷分析提供理论依据。

1 多档货运索道的基本结构及参数

1.1 货运索道的基本结构

货运索道的基本结构如图1所示，其中：支架包括横梁、支腿、安装于横梁下方的承载索鞍座及牵引索滚轮；牵引索拖动载货小车（含运行小车和载荷）经过支架鞍座。

图1 货运索道基本结构Fig.1 Basic structure of freight ropeway

根据承载索特点，货运索道可分为固定式索道与可滑移式索道。固定式索道的承载索与支架鞍座间固定，不产生相对滑动，且支架间承载索的长度不变；可滑移式索道的承载索与支架鞍座间不固定，可产生相对滑动。

1.2 多档货运索道的架设参数

对于具有n个档的索道，索道各档的档距及高差（档两端支架鞍座的高度差）分别为Ld、hd（d=1，2，…，n）。图2所示为3档货运索道。

图2 3档货运索道示意图Fig.2 Diagram of freight ropeway with three spans

1.3 载货小车与牵引索的参数

如图3所示，设在多档货运索道上共有m辆载货小车Pj（j=1，2，…，m），载货小车的重力为Gj。载货小车固定在牵引索上，其间共有m-1段牵引索，其长度分别为sPj（j=1，2，…，m-1）；首个支架与第1辆载货小车间的牵引索的长度为sP0，最后1辆载货小车与最后1个支架间的牵引索的长度为sPm。在运输过程中，载货小车间的牵引索段在牵引力、载货小车重力的作用下产生弹性延伸。

图3 载货小车与牵引索的参数示意图Fig.3 Diagram of parameters of freight car and traction cable

1.4 工作索索段编号

计算时以仅受自重作用的悬链线为基本单元，因此以载货小车及支架为节点，将工作索分为n+m个索段。为方便分析，从运行起点起依次对工作索各索段进行1至n+m的编号，每个索段的起点记为A，终点记为B，可知：共有n个索段以支架节点为B点，令其序号为k1，k2，…，kn；共有m个索段以重物为B点，令其序号为g1，g2，…，gm。

2 工作索的张力分析

工作索索段可视为仅受重力作用的弹性悬链线，各索段i（i=1，2，…，n+m）的档距、高差可分别表示为［8］：

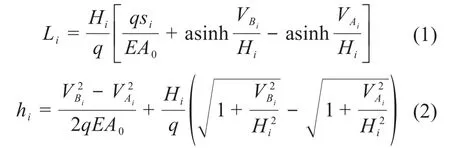
式中：q为每米索段的重力；E为工作索的弹性模量；A0为工作索的截面面积；si为各索段的初始长度（无载荷情况下）；Hi为各索段的水平张力；VAi为各索段起点的垂直张力；VBi为各索段终点的垂直张力。

各索段起点和终点的垂直张力的关系为：

各索段起点和终点的切向张力可表示为：

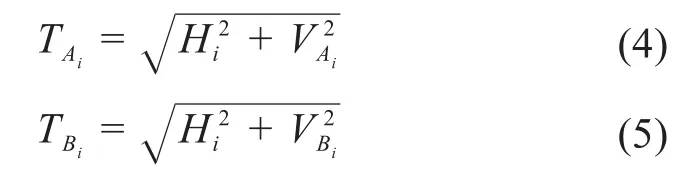
由上述公式可以看出，工作索各索段的档距、高差和切向张力等主要参数均与索段的初始长度si、水平张力Hi、A点垂直张力VAi有关。因此，可以si、Hi、VAi为基本变量，开展多档货运索道承载索与牵引索耦合作用下分段悬链线分析与计算方法的研究。

基于货运索道的结构参数及其工作索张力的分析，从结构守恒及力平衡两个方面分析多档货运索道的承载索、牵引索与载货小车之间的耦合作用。

3 工作索结构守恒分析

在多档货运索道的运行过程中，与工作索总体结构相关的一些参数不会发生变化，以此可建立相应的守恒方程。

3.1 承载索与牵引索的档距和高差相等

如图3所示，可以认为承载索与牵引索各索段的档距和高差相等，即：

式中：Llj、Ltj分别为承载索与牵引索各索段的档距；hlj、htj分别为承载索与牵引索各索段的高差；下标l、t分别表示承载索和牵引索，下同。

3.2 各档内工作索的总档距及总高差守恒

在多档货运索道运行过程中，索道各档内的工作索索段的档距总和始终等于该档的档距，各索段的高差总和始终等于该档的地形高差，即：

3.3 载货小车间牵引索长度守恒

载货小车被牵引索连接牵引，多档货运索道运行时载货小车间可能包含1个或多个牵引索索段。如图4所示，载货小车Pj+1和Pj+2之间包含牵引索索段i+1和i+2。

分别建立载货小车间牵引索索段的长度守恒方程及最后1个载货小车与末端支架间牵引索索段的长度守恒方程：

图4 载货小车间牵引索分段示意图Fig.4 Diagram of segmented traction cable between freight cars

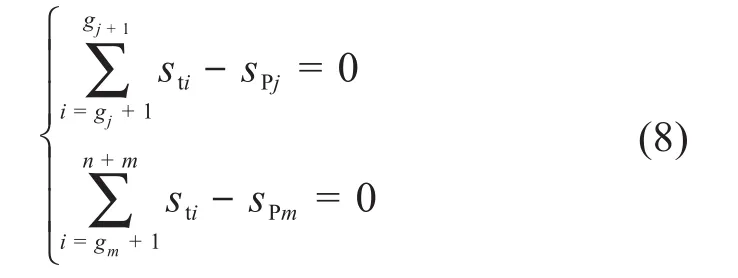
3.4 承载索长度守恒

1）固定式索道承载索档内长度守恒。

固定式索道各档内承载索的总长度不随索形、载重等因素变化，可表示为：

式中：sld为第d档承载索总长度，可通过测量得到。

2）可滑移式索道承载索总长度守恒。

可滑移式索道各档内承载索的总长度随承载索滑移量变化而变化，但其首末端点间的总长度不变，则有：

式中：sl0为承载索总长度，可通过测量得到。

4 工作索张力平衡分析

4.1 载货小车两侧工作索的张力平衡

设载货小车左侧工作索索段的序号为j，右侧序号为j+1。载货小车通过滚轮与承载索发生接触，如图5（a）所示。忽略滚动摩擦时，小车前第j个承载索索段终点Bj的切向张力与小车后第j+1个承载索索段起点Aj+1的切向张力相等，即：

载货小车同时受到承载索的提升力、牵引索的牵引力与重物的重力，并达到平衡，如图5（b）所示。分别建立载货小车水平方向及垂直方向的力平衡方程：

4.2 支架两侧牵引索的张力平衡

由图6可知，忽略滚动摩擦力时，支架前第d个牵引索索段终点Bd的切向张力与支架后第d+1个牵引索索段起点Ad+1的切向张力相等，即：

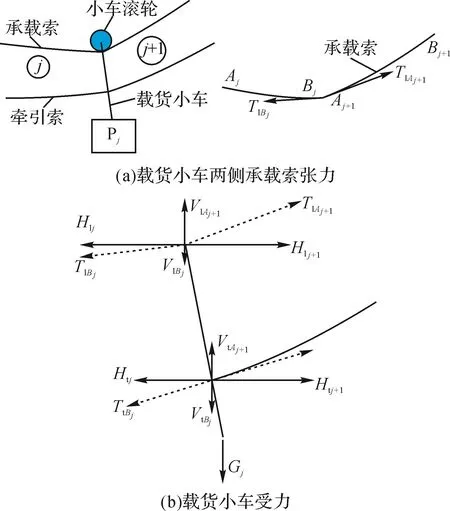
图5 载货小车及其两侧工作索受力分析Fig.5 Force analysis of freight car and working cables on both sides of car

图6 支架两侧牵引索受力分析Fig.6 Force analysis of traction cable on both sides of bracket

4.3 可滑移式索道支架两侧承载索的张力平衡

对于可滑移式索道，其第d个支架的承载索与鞍座摩擦时承载索的张力分析如图7所示。鞍座对承载索的摩擦力由承载索对鞍座的压力与摩擦系数确定，可表示为：

式中：μ为承载索与鞍座之间的摩擦系数；Nd为承载索对鞍座的压力。

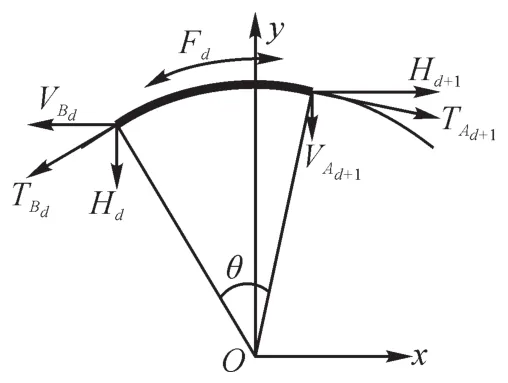
图7 与鞍座摩擦时承载索受力分析Fig.7 Force analysis of bearing cable rubbing against saddle

由于接触段弧度较小，根据文献［17］，Nd为平均切向张力与包角的乘积，即：

因此，可建立可滑移式索道支架鞍座前后承载索的切向张力平衡方程：

5 表征工作索耦合作用的方程组及其求解

根据上述多档货运索道工作索结构守恒及力平衡关系的分析，可以建立完整的表征工作索耦合作用的方程组。

5.1 表征工作索耦合作用的非线性方程组

以承载索各索段的长度sli、水平张力Hli、A点垂直张力VtAi，以及牵引索各索段的长度sti、水平张力Hti，A点垂直张力VtAi为未知变量，构建表征固定式及可滑移式多档索道工作索耦合作用的非线性方程组，如表1所示。

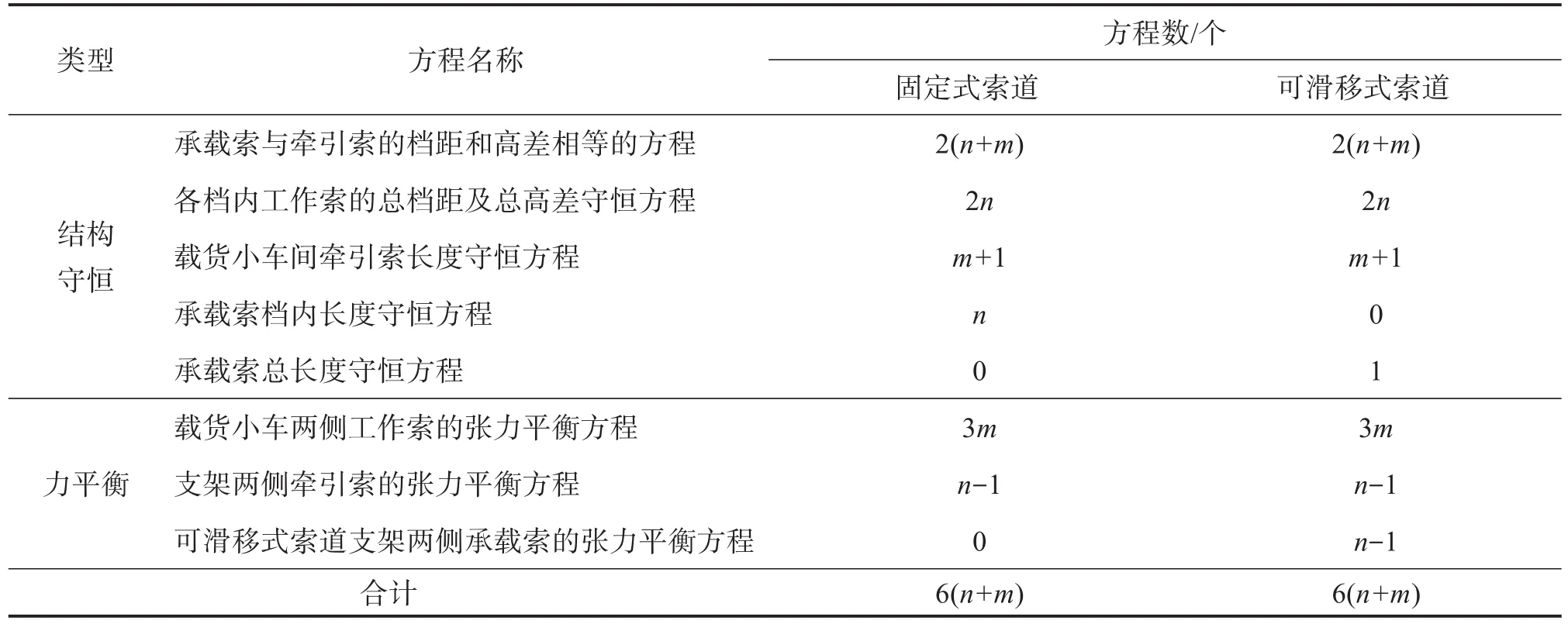
表1 表征多档货运索道工作索耦合作用的方程组Table 1 Equations representing coupling action of working cables of muli-span freight ropeway

由表1可以看出，表征固定式及可滑移式多档索道工作索耦合作用的非线性方程均有6（n+m）个，与未知数个数相等，因此该方程组闭合，将其表示为：

5.2 非线性方程组求解

方程组（18）的非线性较强，而普通计算方法的收敛性差，迭代速度慢，无法满足工程应用中快速、准确求解的要求，因此本文采用牛顿迭代法进行求解。

6 工程实例

为验证本文计算方法的可行性，以特高压输电线路建设工程为例，开展固定式与可滑移式多档货运索道现场运行试验，试验现场如图8所示。试验中测量并记录承载索的切向张力及可滑移式索道承载索的滑移量。

图8 多档货运索道运行试验现场Fig.8 Operation test site of muli-span freight ropeway

试验在3档货运索道上进行，索道各档的档距和高差如图9所示。承载索直径为22 mm，弹性模量为110 GPa，单位质量为1.8 kg/m；牵引索直径为13 mm，弹性模量为100 GPa，单位质量为0.6 kg/m。

为便于表述，索道中每一档靠近起始支架的承载索的测量点为a点，靠近另一端支架的承载索的测量点为b点。

1）双载荷工况下固定式索道承载索的张力。

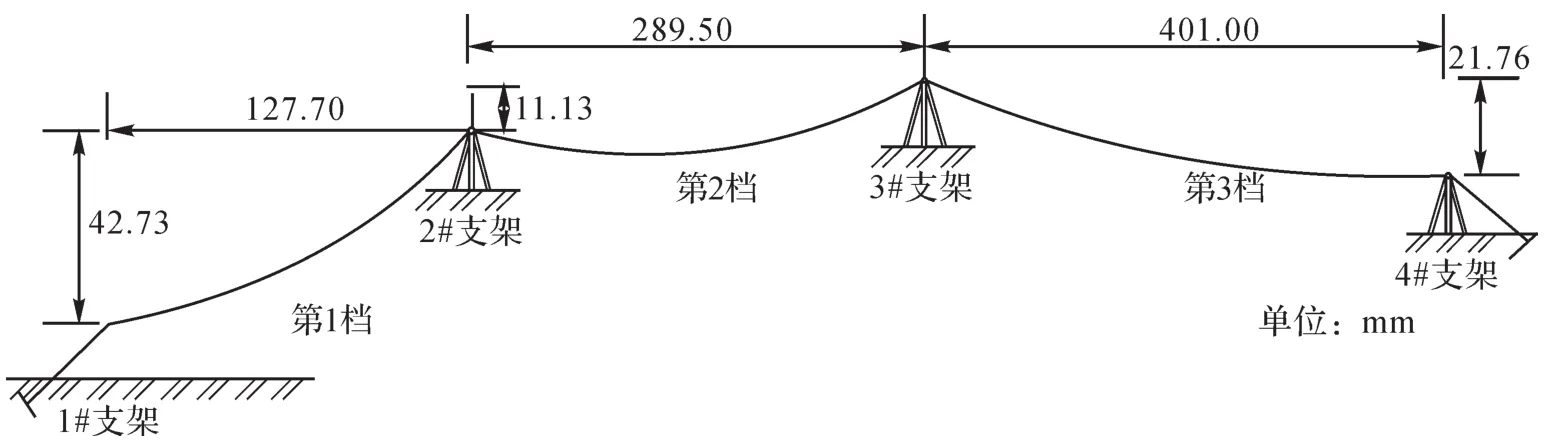
图9 3档货运索道的档距和高差示意图Fig.9 Diagram of distance and height difference of freight ropeway with three spans

在第2档索道内距2#支架40.0 m处悬挂660 kg载荷，在第3档索道内距3#支架43.3 m处悬挂450 kg载荷。在载荷沿承载索运行210 m的过程中，承载索张力的试验值与计算值如图10和图11所示，图中载荷水平位置起点分别为2#支架、3#支架所在的水平位置。

图10 固定式索道第2档内b点处承载索切向张力的试验值与计算值对比Fig.10 Comparison of test values and calculated values of tension force of bearing cable at point b of the second span of fixed ropeway

图11 固定式索道第3档内a点处承载索切向张力的试验值与计算值对比Fig.11 Comparison of test values and calculated values of tension force of bearing cable at point a of the third span of fixed ropeway

由图10和图11可知，固定式索道各档内承载索切向张力计算值与试验值的变化趋势一致。在固定式索道运行过程中，第2档内b点处承载索最大张力的试验值为40.63 kN，计算值为41.11 kN，相对误差为1.17%；第3档内a点处承载索最大张力的测量值为39.15 kN，计算值为36.24 kN，相对误差为7.44%。

2）单载荷工况下可滑移式索道承载索的张力。

在第3档索道内距3#支架11 m处悬挂450 kg载荷，载荷沿承载索运行114 m，可滑移式索道各档内承载索的切向张力的试验值与计算值对比如图12至图14所示，图中载荷水平位置起点为3#支架所在的水平位置。

图12 可滑移式索道第1档内a点处承载索切向张力的试验值与算值对比Fig.12 Comparison of test values and calculated values of tension force of bearing cable at point a of the first span of slippable ropeway

由图12至图14可知，在可滑移式索道运行过程中，第1档内a点处承载索最大张力的试验值为23.13 kN，计算值为23.26 kN，相对误差为0.55%；第2档内b点处承载索最大张力的试验值为26.30 kN，计算值为25.36 kN，相对误差为3.59%；第3档内a点处承载索最大张力的试验值为28.38 kN，计算值为29.76 kN，相对误差为4.87%。

3）可滑移式索道承载索的滑移量。

在上述单载荷工况下，可滑移式索道各档内承载索与支架鞍座间的滑移量如图15和图16所示。由图可知，在2#支架、3#支架处承载索滑移量计算值与试验值的变化趋势一致。2#支架处承载索最大滑移量的试验值为0.094 m，计算值为0.089 m，相对误差为5.32%；3#支架处承载索最大滑移量试验值为0.577 m，计算值为0.557 m，相对误差为3.47%。

图13 可滑移式索道第2档内b点处承载索切向张力的试验值与计算值对比Fig.13 Comparison of test values and calculated values of tension force of bearing cable at point b of the second span of slippable ropeway

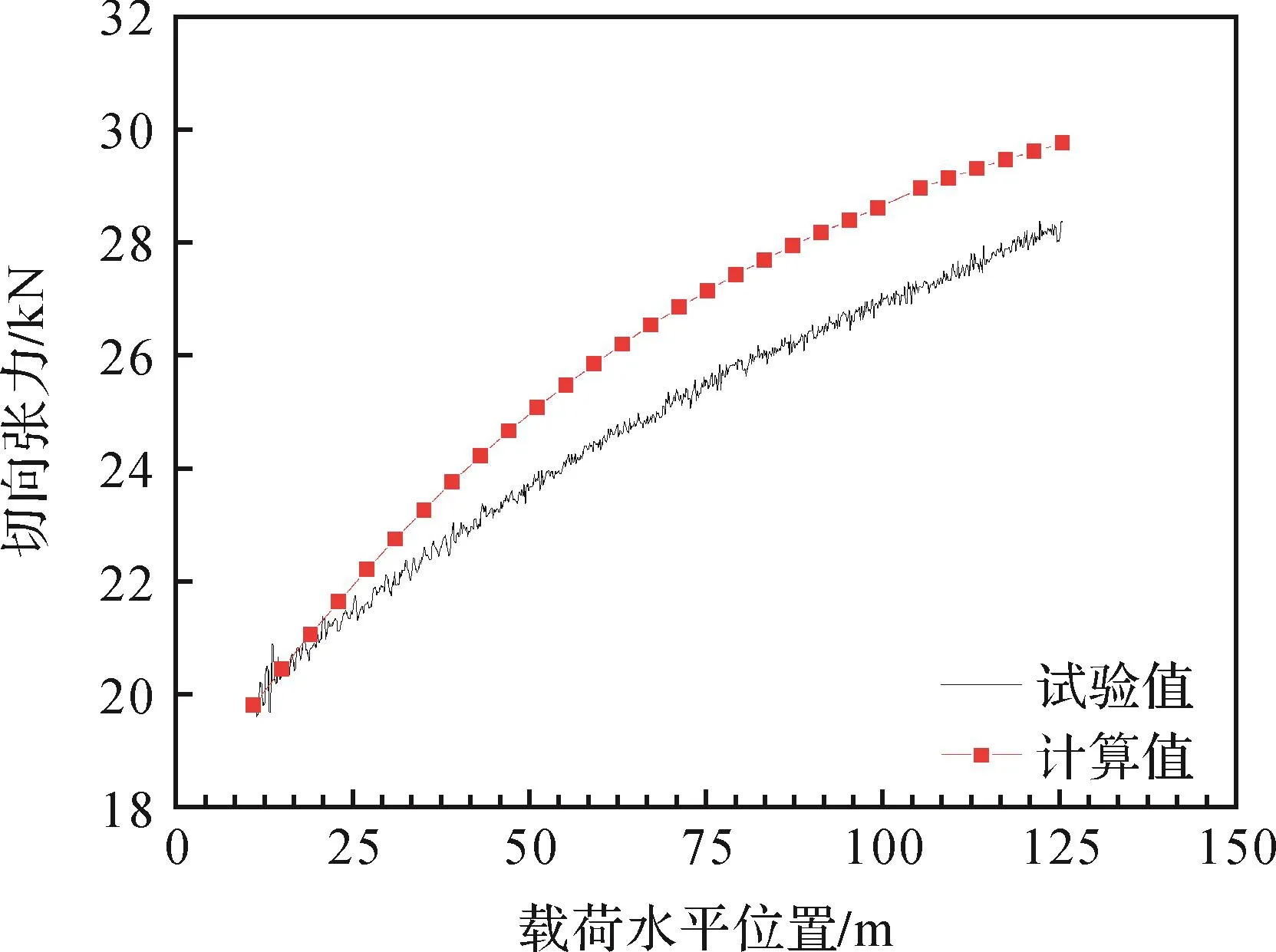
图14 可滑移式索道第3档内a点处承载索切向张力的试验值与计算值对比Fig.14 Comparison of test values and calculated values of tension force of bearing cable at point a of the third span of slippable ropeway

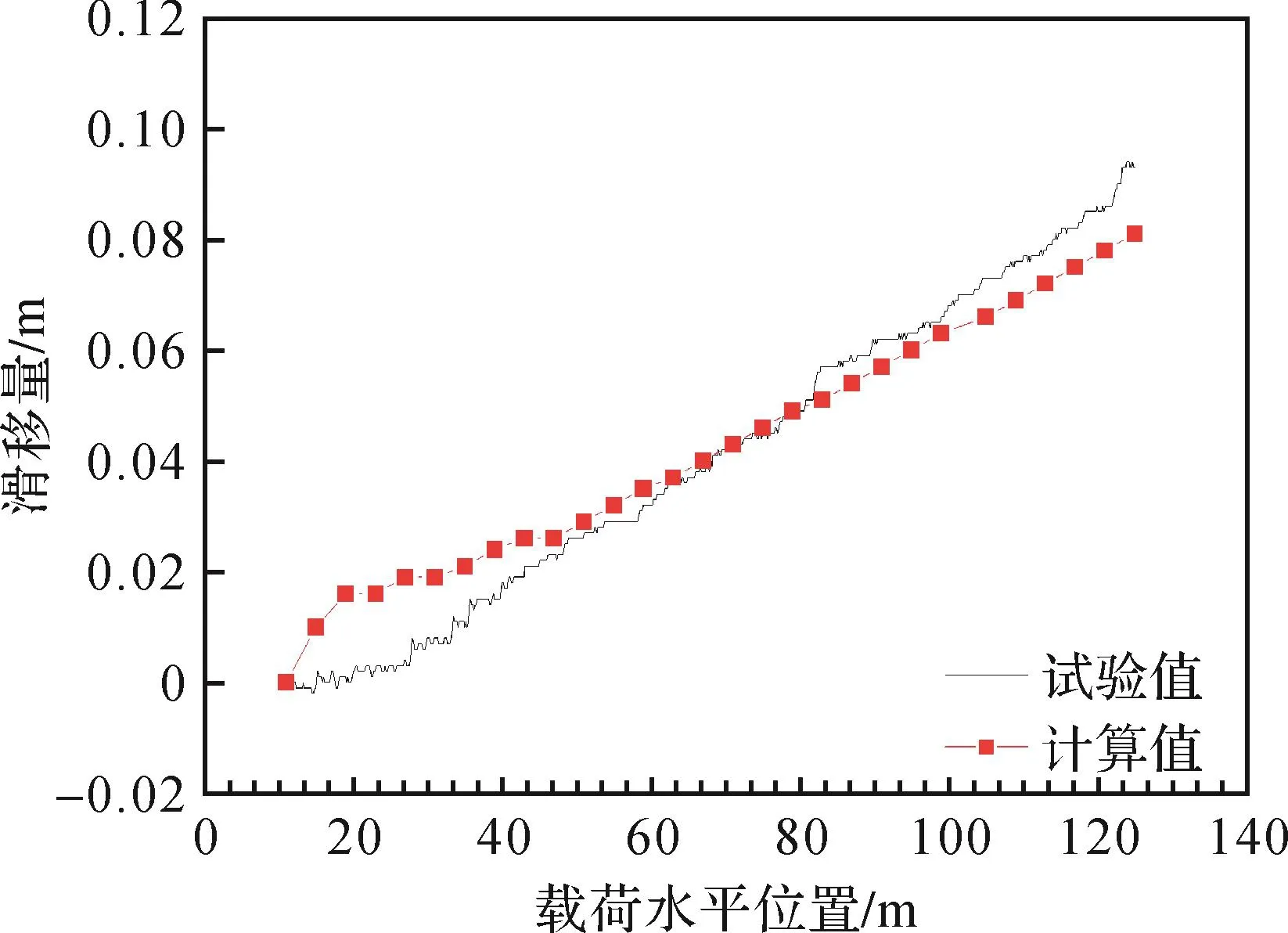
图15 2#支架处承载索滑移量的试验值与计算值对比Fig.15 Comparison of test values and calculated values of slippage of bearing cable at 2#bracket

图16 3#支架处承载索滑移量的试验值与计算值对比Fig.16 Comparison of test values and calculated values of slippage of bearing cable at 3#bracket

7 结 论

本文提出了多档货运索道工作索耦合作用下分段悬链线的分析与计算方法，从工作索结构守恒、张力平衡两方面建立了工作索耦合作用的计算方程组。

结果表明提出的计算方法满足工程应用条件，能够计算在任意载荷作用下多档货运索道承载索、牵引索的张力，支架所受作用力，承载索与支架鞍座间滑移量等索道设计的关键参数。通过对比多档货运索道承载索张力、滑移量的试验值与计算值发现，试验值与计算值吻合良好，承载索最大张力、滑移量的相对误差均不超过8%，完全满足索道设计要求，可有效解决固定式与可滑移式两类多档货运索道各部件受力分析与计算及设计选型问题。