含时变延迟且控制方向未知的自适应迭代学习
夏元天,周菊香,徐天伟
(云南师范大学 民族教育信息化教育部重点实验室,昆明 650000)
0 概述
自动化系统在建模和实际应用过程中存在不确定性和不精确性的问题,使用传统的PID控制、最优控制等技术难以解决上述难题。迭代学习控制(Iterative Learning Control,ILC)[1-3]和重复控制(Repeat Control,RC)[4-5]很早被提出且得到了很好的发展。ILC作为一种克服传统控制设计局限性的有效控制技术[6-7],其善于在有限的时间间隔内处理重复的控制任务。文献[1-3]提出一种新的ILC方法用来补偿基于收缩映射的ILC。文献[8]针对一类具有延迟性能的线性系统提出一种ILC协议。文献[9]提出一种基于PID-type的ILC算法。总的来说,ILC以其良好的全时间间隔轨迹跟踪性能已广泛用于各类控制领域。
受控系统的时延效应会降低系统性能,甚至会导致系统瘫痪。文献[10]引入分离技术,用以解决时延效应带来的影响。文献[11]为了解决一类不确定非仿射非线性时变时滞系统的自适应控制问题,提出一种新的拉祖米钦-努斯鲍姆引理。文献[12]通过引入饱和函数,构造出一种新的ILC机制。文献[13]针对不确定非线性时变时滞系统中存在的非仿射非线性故障问题,提出一种基于模糊逼近的自适应容错跟踪控制方法。文献[14]利用神经逼近技术和努斯鲍姆函数法设计一种自适应ILC方案。文献[15]提出一种自适应迭代学习控制(AILC)方案,用以解决一类具有未知时变延迟和输入饱和的非线性参数化系统。文献[16]针对一类具有未知时变参数和时变时滞的非线性系统,通过参数分离技术并结合信号替换机制,提出了一种新的AILC方法。
控制方向在系统的设计过程中起着关键性的作用。Nussbaum增益技术则是解决控制方向未知问题的一种常用方法[17-18]。文献[19]提出一种跟踪周期轨迹的连续通用重复学习控制方法。文献[20]将Nussbaum增益技术引入至Backstepping方法中,以解决控制方向未知的船舶航向系统的稳态性能控制问题。文献[21]采用参数分离技术和信号置换思想来处理系统中出现的时滞项,利用Nussbaum增益技术解决未知控制方向等问题。文献[22]提出一种数据驱动的约束范数最优迭代学习控制框架,用以解决跟踪问题和点对点运动问题。文献[23]提出一种基于倒推和DSC相结合的自适应径向基函数神经网络控制方法。文献[24]通过变换系统形式和采用Butterworth低通滤波器解决控制方向未知的问题。文献[25]提出一种新的基于截断的调节方法,使算法能够自适应地找到正确的控制方向。文献[26]提出一种基于障碍Lyapunov函数的反步自适应控制方法,首次解决了控制方向未知的全状态约束非线性系统的跟踪控制问题。文献[27]在不使用努斯鲍姆增益的情况下,提出一种求解离散系统未知控制方向问题的新方法。文献[28]提出一种鲁棒自适应迭代学习控制算法。
本文在上述研究的基础上进行改进,设计一种新的自适应迭代学习策略。利用微分-差分耦合型参数自适应律解决了双线型参数中存在的时变和时不变类型的问题。使用局部的李普希茨连续条件,使得非参数化得到了良好的处理。将Nussbaum技术与ILC方法相结合,解决了系统中存在的控制方向未知问题。基于信号替换思想和参数重组技术,将具有时延的所有项组合成新的时变参数,使得时变延迟问题得到了解决。
1 问题描述
本文设计的自适应迭代学习策略可表示为:
(1)
其中,t∈[0,T],T>0且为已知常数,xi(t)∈R为系统状态,ui(t)∈R为控制输入,ϑ(t)∈R为随时间变化的连续型参数且未知,θ∈R是与时间变化无关的连续型参数且未知,并假设其大于零。ξ(xi,t)为非线性连续函数且已知,f(,)是未知连续函数,g(xi,t)为未知的非线性函数,满足局部Lipschitz连续,τ(t)∈C[0,T]为未知时变延迟,且满足τ(t)≤τmax,∀t∈[0,T],τmax为已知常数,i∈Z+为迭代次数,v(t)给出了起始条件且为已知的连续型函数,b(t)≠0为时变参数且未知,控制方向由其正负决定。


假设2f(,)满足李普希茨连续条件,即:
|f(xi(t-τ(t)),t)-f(xd(t-τ(t)),t)|≤
l(|xi(t-τ(t))-xd(t-τ(t))|)
其中,l为未知的李普希茨常数。
假设3xi(0)=xi-1(T),xd(0)=xd(T)。
假设4系统1满足xi(t)=xd(t),t∈[-τmax,0],显然ei(t)=0,t∈[-τmax,0],∀i∈Z+。
假设5g(x,t)是未知非线性函数且满足李普希茨连续条件,即:



定义1v(·)为Nussbaum函数,且满足以下条件:
(2)
引理1v(·)和k(·)在[0,tf]上为光滑函数,∀t∈[0,tf],V(t)≥0,b(t)在B=[b-,b+],0∉B内取值。若式(3)成立:
(3)

2 自适应迭代学习控制设计
下式为ei的k次迭代方程:

b(t)ui(t)+g(xi,t)+f(xd(t-τ(t)),t)-
f(xd(t-τ(t)),t)]=ϑ(t)ξ(xi,t)θ+
b(t)ui(t)+g(xi,t)+φ(t)+Λi
(4)
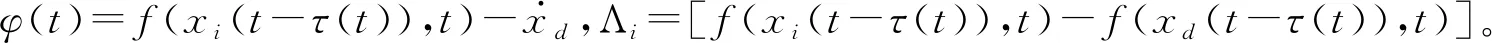
由假设2可知,Λi满足以下条件:
|Λi|≤l(|xi(t-τ(t))-xd(t-τ(t))|)≤
l(|ei(t-τ(t))|)
(5)
针对系统1设计一个处理时变时延迟的李雅普诺夫函数,具体如下所示:
(6)
由式(6)给出Lyapunov函数的导数如下所示:
(7)
将式(4)代入式(7)可得:

(8)
由式(5)可得:
eiΛi≤|ei||Λi|≤l|ei||ei(t-τ(t))|
(9)
(10)
将式(10)代入式(8)可得:





ei[ϑ(t)ξ(xi,t)θ+b(t)ui(t)+g(xi,t)-
ei[ϑ(t)ξ(xi,t)θ+b(t)ui(t)+g(xd,t)+φ(t)+
(11)
由假设5得到:
(12)
将式(12)代入式(11)中,得到:

(13)
第i次迭代的控制律为:
(14)

ϑ(t)的学习律为:
(15)
θ的学习律为:
(16)
L的学习律为:
(17)

(18)



(19)




(20)



3 收敛性分析
定理1系统(1)在假设1~假设5、学习控制律式(14)以及参数学习律式(15)~式(17)下,保证了:

2)闭环系统所有信号有界。
证明构造的Lyapunov泛函为:

(21)
对任意t∈[0,T],V(t)在区间[0,T] 上的差分为:
ΔV(t)=(V1,i(t)-V1,i-1(t))+


(22)

根据式(4)和式(14)计算式(22)右边第1项可得:

α(xi,xd,t)ei(t)]dσ+V1,i(0)-V1,i-1(t)=

V1,i(0)-V1,i-1(t)
(23)


(24)
根据参数学习律式(16),计算式(22)右边第4项可得:
(25)
根据式(17),计算式(22)右边第5项可得:
(26)
将式(23)~式(26)分别代入式(22)可得:




(27)

(28)
重复利用式(28)可以得到:
(29)

(30)
进一步得到Vi(t)的倒数为:

(31)
表示E(t+(i-1)T)=Vi(t)。对∀t∈[0,T],由式(29)~式(31)可得:
(32)
当i→,可以得到:
(33)
下面证明V0(T)的有界性。
对任意∀t∈[0,T],V0(t)的倒数为:
(34)
对式(34)两端从0到T进行积分可得:
(35)


(36)
ϑ(t)在[0,T]上是连续型函数,因此ϑ(t)在[0,T]上为有界函数,综合已知条件得,存在M1,M2,M3,M4使下式成立:

(37)
将式(37)代入式(36)可得:
V0(0)=M1+M2+M3+M4<
(38)

证明结束。
4 实例仿真
不确定系统:
目标轨线:
xd(t)=cost

在仿真实验中取:t∈[0,2π],η=0.5,c=0.5,q1=0.5,q2=0.4,q3=0.5
1)当b(t)>0时,取b(t)=5+0.2sin(πt)。通过仿真实验得出系统中各参数的迭代曲线图如图1~图6所示。

图1 最大跟踪误差|ei|sup变化曲线1

图2 Nussbaum型函数v(·)变化曲线1

图3 时变参数ϑ(t)的变化曲线1

图4 时不变参数θ的变化曲线1

图5 时不变参数L的变化曲线1

图6 控制器ui(t)的变化曲线1
2)当b(t)<0时,取b(t)=-(5+0.2sin(πt))。通过实验仿真,得出系统中各参数的迭代曲线图如图7~图12所示。

图7 最大跟踪误差|ei|sup的变化曲线2

图8 Nussbaum型函数v(·)的变化曲线2

图9 时变参数ϑ(t)的变化曲线2

图10 时不变参数θ的变化曲线2
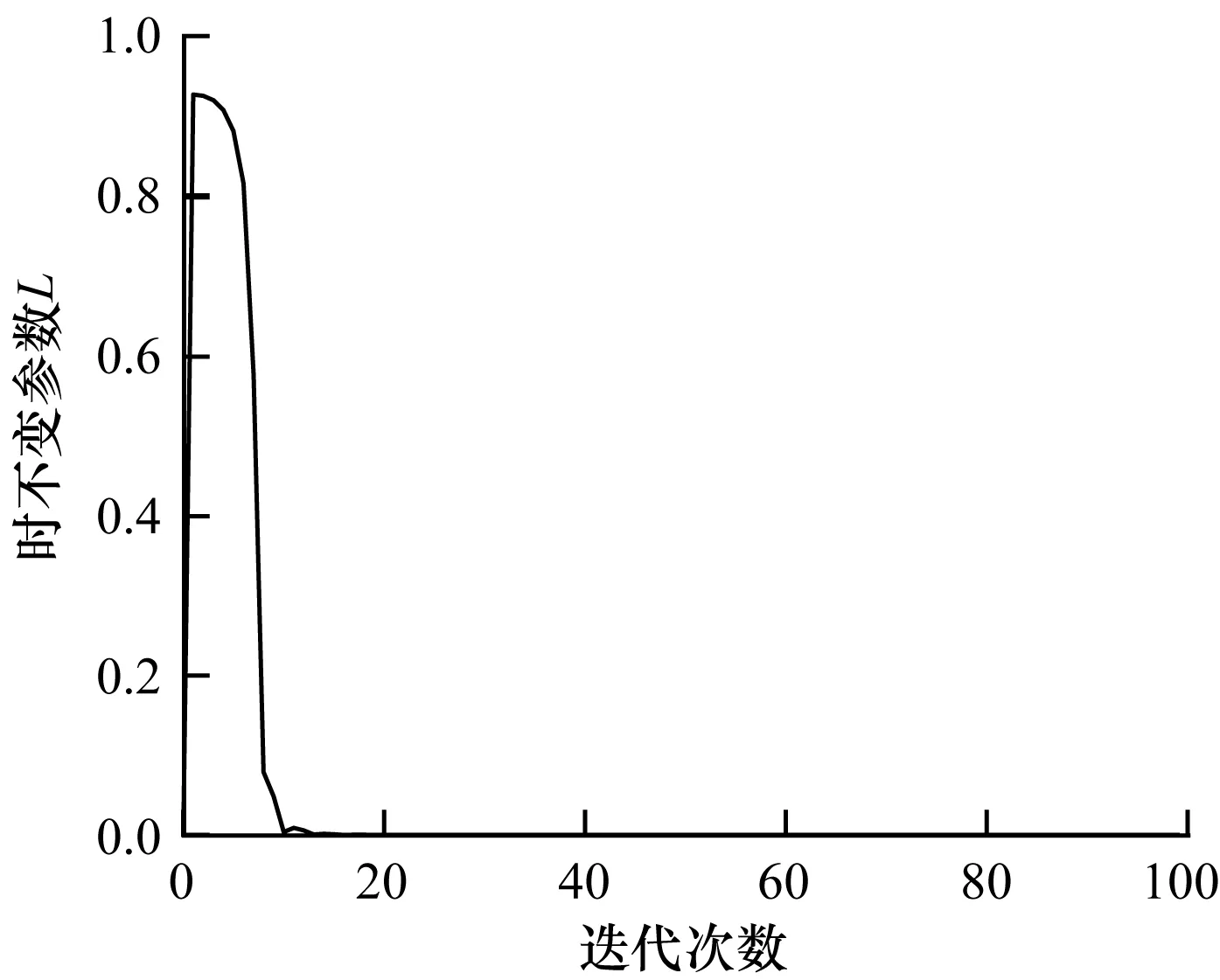
图11 时不变参数L的变化曲线2

图12 控制器ui(t)的变化曲线2
从图1~图12可以看出,本文设计的非线性系统在迭代次数小于20次的情况下,系统的最大跟踪误差和Nussbaum型函数已经开始收敛于0。根据文献[29]设计的非线性系统以及提供的仿真结果表明,在方向为非时变常参数且不包含时变延迟的情况下,其系统最大跟踪误差以及Nussbaum型函数在迭代次数120次以上才开始趋于收敛于0。通过与文献[29]比较可得出,在时变未知控制方向和含有时变延迟的双重不确定条件下,本文设计的系统依然能够以较少的迭代次数以及较高的执行效率运行,也说明了本文系统在时效上的优越性和可行性。
5 结束语
本文针对控制方向未知且含有非线性延迟及参数和非参数化的不确定性系统进行了深入分析。利用Nussbaum函数和通过导入差分耦合型更新定律,并结合Lyapunov函数给出系统收敛的充分条件,设计出全新的自适应迭代方案,使跟踪误差最终收敛于0,并证明各信号的有界性。仿真结果证明了本文设计的合理性以及结果的可行性。
通过以上理论推导和实验仿真结果说明本文设计的自适应迭代学习策略在一阶系统中的有效性。在下一步研究工作中,可以考虑将其应用到二阶或高阶的非线性不确定系统中,通过与其他相关技术相结合,用以解决未知控制方向和时变延迟对高阶不确定系统产生的影响。

