基于高斯混合-变分自编码器的轨迹预测算法

张显炀,朱晓宇,林浩申,刘 刚,安喜彬

(火箭军工程大学 核工程学院,西安 710025)

0 概述

轨迹预测的目的是通过分析移动目标的历史轨迹挖掘数据特征,从而得到轨迹数据模型,进一步实现轨迹的时空预测[1]。通过对舰船的历史轨迹数据建模并研究相应的求解算法进行舰船轨迹预测,可以为海洋作业如海上搜救、海洋运输等提供重要保障。海面舰船与地面道路车辆的不同主要有两点:一是轨迹约束不同,海面舰船轨道约束和速度约束弱,其运动的随机性较大,运动模式多样,运动规律多变;二是轨迹数据来源方式不同,车辆轨迹数据通常可以通过GPS定位得到,而海面舰船的轨迹一般是通过侦察卫星观测而来,其轨迹是离散的数据点,且受到卫星观测精度的影响,轨迹数据特征进一步复杂化。因此,将传统的地面车辆轨迹预测方法应用于海面舰船上不能得到良好的预测结果,但是海洋作业又对舰船轨迹预测精度和实时性提出较高的要求。

当前轨迹预测常用的方法有卡尔曼滤波器(Kalman Filter,KF)[2-3]、隐马尔科夫模型(Hidden Markov Model,HMM)[4]和高斯混合模型(Gaussian Mixture Model,GMM)[5]。卡尔曼滤波器具有线性、无偏、方差小等特点,被广泛用于预测问题,但是该方法需要做大量的矩阵运算从而缺乏实时性,常用于道路车辆等运动模型简单的目标的轨迹预测。隐马尔科夫模型本质上是对时间序列的预测,但是对噪声没有较好的鲁棒性,并且随着数据集的增大,预测误差会不断累积。高斯混合模型是一种被广泛应用的基于概率统计的预测模型,模型中的轨迹数据由多个高斯过程线性组合产生,通过高斯混合建模并使用最大似然估计(Expectation-Maximization,EM)算法求取模型参数,再通过高斯混合回归实现轨迹预测。文献[6]表明,对于轨迹数据较多的情况,GMM方法在预测精度和实时性上性能均优于KF和HMM方法。目前,GMM方法在车辆轨迹预测[7-8]、智能交通[9]、数据聚类[10-11]等领域都得到了较好的应用。由于车辆的行进轨迹受到道路、速度等诸多约束,其移动规律和数据特征较为简单,因此GMM的预测误差小。但是当数据的复杂度提高时,GMM方法不再具有良好的适用性,并且随着数据集的增大,GMM方法的计算代价也会指数级增加。因此,针对舰船轨迹的特征,亟需研究计算代价低、预测精度高的轨迹预测算法。

轨迹预测的本质是通过训练模型获得模型参数,再利用模型进行预测生成,这与变分自编码器(Variational Autoencoder,VAE)[12]的设计思想相近。变分自编码器是当前被广泛应用的一种无监督生成模型[13-14],能够解决无标签的机器学习问题[15-16]。它通过神经网络将原始的高维数据编码到低维的隐空间,再根据解码网络生成原始数据的逼近值。在经典的变分自编码器中,隐变量的后验分布通常被假设为简单的分布,例如标准正态分布,这导致低维隐空间的表示和对隐空间的特征描述过于简单,一旦原始训练数据集复杂度提高,模型生成的精度将达不到要求。为解决该问题,文献[17-18]通过假设更复杂的先验分布形式来提高模型生成和预测的准确性。如何将VAE方法应用到轨迹预测问题上,并通过合理假设隐空间的先验分布,使其更符合真实的数据分布,是当前需要解决的问题。

本文研究海面舰船的轨迹预测问题,提出一种基于高斯混合先验-变分自编码器(GMVAE)的轨迹预测算法。将轨迹坐标转化为轨迹矢量,并以位移矢量表示预测目标的位置坐标,利用VAE完成轨迹特征的提取与生成预测。针对海面舰船的轨迹数据特点,将隐空间的先验分布假设为混合高斯分布,使其更符合真实的数据特征,同时在隐空间引入类别标签,完成对数据特征的分类。

1 海面舰船轨迹预测模型

1.1 轨迹预测问题描述

海面舰船的轨迹数据通常由卫星观测获得[19],因此,舰船的轨迹由离散的经纬坐标点构成。本文假设舰船在二维平面上移动,将上述经纬度坐标看作平面坐标,以T表示n条轨迹组成的数据集:

T={T1,T2,…,Tn}

(1)

Ti={(xi1,yi1),(xi2,yi2),…,(xil,yil)}

(2)

其中,Ti表示第i条轨迹,(xij,yij)表示第i条轨迹在j时刻的坐标点,l是第i条轨迹数据的长度,即该条轨迹包含坐标点的数量。

假设舰船轨迹在x和y方向上相互独立,在本文中,均以x方向上的轨迹预测问题为例,y方向上的同理可得。设x轴方向上的真实轨迹数据集为X:

X=(x1,x2,…,xn)T

(3)

(4)

(5)

其中,ψλ表示轨迹预测模型,λ表示模型参数。

在通常情况下,轨迹数据集X较大,如本文的仿真数据集就包含约10 000条轨迹。KF方法是对每条轨迹进行逐条预测,加上大量的矩阵运算必然导致计算代价高。HMM方法虽然不必逐条预测,但是其预测误差会随着预测长度的递增不断累积,本身的迭代计算复杂度也非常高。因此,上述两种算法均不适用于舰船的轨迹预测。GMM方法虽然可以避免大量的矩阵运算,在一些简单的轨迹预测问题上,其实时性和精度均优于上述两种算法[6],但是该方法需要计算完整轨迹数据的对数似然关于某个分布的期望,对于复杂度很高的舰船轨迹数据,其耗时会随着数据集的增大呈指数级增长,这在实际的预测中是不可取的。为解决样本数据集增大带来的计算代价增大问题,同时又保证轨迹预测精度,本文提出一种基于变分自编码的轨迹预测算法。

1.2 基于变分自编码器的轨迹预测算法

图1 变分自编码器结构

2 基于改进变分自编码器的轨迹预测算法

本节首先对舰船轨迹数据集进行矢量化和归一化处理,得到轨迹运动矢量集,从而与变分自编码器结合完成轨迹的特征提取与生成预测;然后改进了经典VAE的隐空间网络结构,从而进一步提高轨迹预测精度。

2.1 海面舰船轨迹数据预处理

2.1.1 轨迹矢量集转化

V={V1,V2,…,Vn}

(6)

2.1.2 数据归一化

为使VAE的训练过程能够收敛到最优解,需要对上述矢量集数据进行归一化处理。归一化公式如下:

(7)

其中,xmax、xmin为输入轨迹数据的最大值和最小值。按照上述归一化公式,可以得到模型的输入Vnormal。

2.2 VAETP算法

在基于经典VAE的轨迹预测算法(VAETP)中,编码网络将轨迹数据映射到隐空间Z以提取数据特征,得到隐变量z的后验分布。引入标准高斯分布作为z的先验分布,通过最小化后验与先验分布之间的KL距离,达到训练编码网络参数的目的。预测的轨迹数据通过从z中采样和解码获得。在采样过程中,为了能够进行参数更新,使用了参数重构[11]方法,对于小样本轨迹数据可以获得良好的预测结果。VAETP网络架构如图2所示。

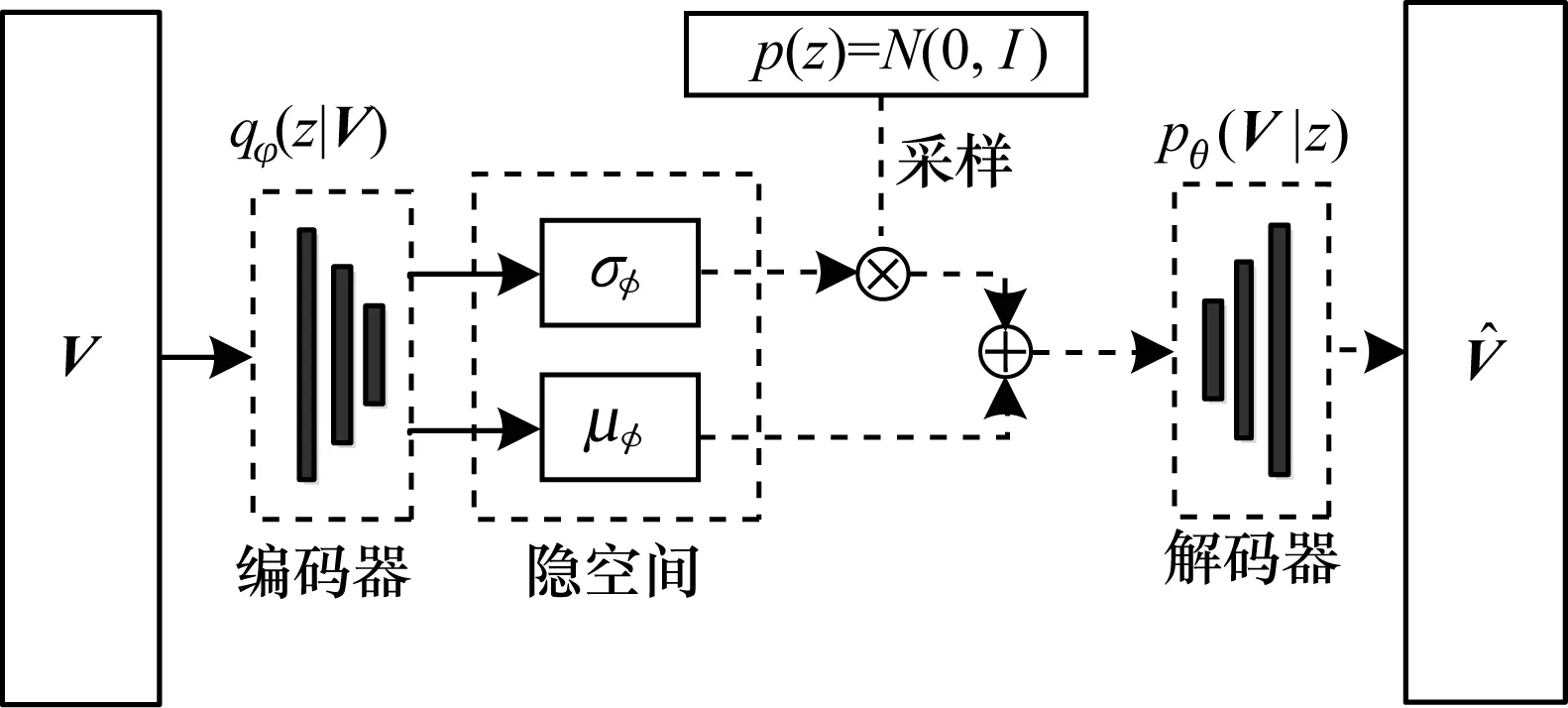
图2 VAETP网络架构

VAE的基本思想是假定轨迹数据V是对某个随机过程采样得到的,每条轨迹样本由隐变量z决定。轨迹数据的生成过程为:首先从先验概率分布pθ(z)中采样得到样本z,然后根据条件概率分布函数pθ(V|z)解码得到轨迹样本,但是生成过程中解码参数θ和隐变量z的信息未知,并且无法计算隐变量z的后验概率qφ(z|V)。所以,VAE统一用神经网络进行拟合。根据边缘概率公式,似然函数[12]可以写为:

logap(V)=DKL[qφ(z|V)||pθ(z|V)]+L(φ,θ;V)

(8)

L(φ,θ;V)=Eqφ[-logaqφ(z|V)+logapθ(z,V)]=

-DKL(qφ(z|V)||pθ(z))+Eqφ[logapθ(V|z)]

(9)

其中,L(φ,θ;V)为变分下界,也是VAE网络的损失函数;φ、θ为编码和解码网络的参数。在式(9)中:第1项称为KL散度项[21],用于衡量后验分布与先验分布的相似程度,通过优化该项可以使得后验qφ(z|V)逼近先验pθ(z),从而防止模型过拟合;第2项是一个对数似然估计,相当于自编码器中的重构误差损失函数,用于重构原始样本数据。由于KL散度的非负性,最大化似然函数问题转化为了最大化变分下界的问题。

VAETP运用Adam算法[22]进行编码和解码网络参数的更新。编码网络的参数φ更新过程如式(10)～式(13)所示,解码网络的参数θ更新过程同理可得。

vi=β1×vi-1-(1-β1)×gi

(10)

(11)

(12)

φi+1=φi+Δφi

(13)

当数据集的复杂度提高,如轨迹数据包含若干种运动模式,或者V的分布是复杂的高维分布时,映射得到的隐空间复杂度随之提高。此时式(9)中z的先验分布对隐空间的描述不能完全刻画原始数据隐空间的特征,从而导致VAETP算法进行轨迹生成和预测精度不够准确。对此,通常的解决方法是先对数据进行分类,再针对每个类别的轨迹数据分别使用VAE训练,最终得到若干个网络。轨迹生成和预测的过程,首先判断轨迹数据所属的类别,再从该类别隐空间中采样得到预测的轨迹。但在实际中,原始轨迹数据往往很难实现有效分类,而且该方法模型的整体契合度不高[23]。

本文提出的轨迹预测算法,通过调整隐空间的先验分布形式使其更符合真实的分布,从而有效地解决VAETP算法采用固定高斯先验缺少变异性的问题,提高预测的精度。该方法不需要事先对轨迹数据进行分类处理,而是直接将轨迹矢量数据编码到隐空间,在隐空间完成轨迹数据的分类,再经过解码得到预测的轨迹矢量,实现端到端的轨迹预测。

2.3 基于GMVAE的轨迹预测算法

本节设计了基于GMVAE的轨迹预测算法。通过2.2节的分析可以看出,在VAETP方法中,隐空间的先验假设过于简单,难以逼近真实的轨迹特征,需要用更复杂的分布来描述。而混合高斯分布几乎可以近似任意复杂的概率分布[24],所以,将隐空间的先验分布假设为混合高斯分布,可以更准确地描述真实的轨迹特征。

图3 GMVAE网络架构

编码和解码过程中变量之间的关系如图4所示,其中,V表示轨迹数据,y代表类别标签,z代表隐变量,φy、φz为编码网络参数,θz、θV为解码网络参数。

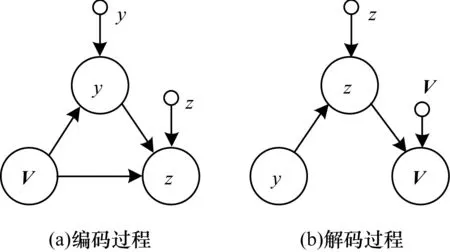
图4 GMVAE编码和解码过程中的变量关系

隐变量y、z编码过程表示为:

qφ(y,z|V)=q(y|V;φy)q(z|V,y;φz)

(14)

其中,q(y|V;φy)表示y的编码过程,q(z|V,y;φz)表示z的编码过程。由此,原始轨迹数据经过编码网络可以得到隐变量z的后验分布:

(15)

在解码过程中,V、y和z的联合概率分布可以描述为:

(16)

(17)

可以看出,隐变量z的先验实际上是一个混合高斯分布。不同的轨迹类别映射到隐空间后对应着不同的高斯分量,每个分量的系数即为y分布的参数π。生成模型p(V|z;θV)通常假设为伯努利分布,损失函数为:

L(θ,φ;V)=Eq(y,z|V)[lnp(V,y,z)-lnq(y,z|V)]=

(18)

3 算法设计与仿真

本节设计GMVTP算法流程,并通过与传统算法GMMTP、VAETP进行比较,检验其算法性能。

3.1 算法流程

轨迹数据经过预处理后,得到的轨迹矢量集Vnormal作为VAE网络的输入。训练过程中选取n=400条轨迹,每条轨迹包含200个轨迹点,设定轨迹类别总数为K=3。本文使用小批量(mini_batch)[25]方法进行训练,将整个训练集划分成若干个小的子训练集,用V_minibatch表示,每个子集的大小batchsize=m。参数更新过程可以表示为:

(19)

算法每次只在一个V_minibatch上更新梯度,而不用遍历完整的数据集,大幅减少了算法收敛所需的迭代次数,而且可以实现并行化计算。

算法1GMVTP算法

输入轨迹矢量集Vnormal={V1,V2,…,Vn}

输出网络参数φ、θ

初始化随机初始化网络参数φ、θ

For i=1:epochs

For j=1:n/m

V_minibatch←{Vj,Vj+1,...Vj+m-1}//取m条轨迹数据

For k=1:m

y←q(y|Vk;φy)//通过编码网络φy生成标签y

μz,σz,z←q(z|y,Vk;φz)//通过编码网络φz生成z的后验

z←N(μ(y;θz),σ2(y;θz))//根据y从相应的先验高斯//分布中采样得到z

Vk|z←B(μ(z;θV))//根据z解码出轨迹Vk

L(θ,φ;Vk)//根据式(17)计算损失函数值

gk←gk-φ,θL(φ,θ;Vk)//计算梯度

End for

gj←gk/m//单个batch数据训练后的梯度更新

φj,θj←φj,θj//根据式(10)～式(13)进行参数更新

End for

End for

轨迹生成模型p(V|z;θV)的神经网络输入层和输出层节点数200,其他网络输出层节点设置为64,迭代次数为epochs。轨迹预测过程为将已知的轨迹前k′(k′<200)个点作为网络输入,经过编码可以得到其类别标签y,再根据标签y从对应的隐空间z中采样解码生成完整的轨迹,即可得到预测出的第k′+1个～第200个轨迹点。

3.2 仿真条件设置

本文使用的轨迹数据集是MIT Trajectory Data。该数据集来源于卫星采集数据,移动目标是在平面上中速移动的机动车辆。因为该轨迹数据在采集类型以及目标运动速度、自由度、路径约束等方面与真实的舰船轨迹类似,所以通过与真实舰船轨迹数据的仿真结果比较,该数据集的仿真结果能够较为真实地反映算法的性能。本文的仿真环境配置为CPU Intel®CoreTMi5-8300H @2.3 GHz,内存8 GB,显卡NVIDIA GeForce GTX 1050Ti,操作系统为Ubuntu16.04。训练过程中的超参数设置如表1所示。

表1 训练过程超参数设置

3.3 仿真结果分析

3.3.1 轨迹训练结果

本节从轨迹数据集中选取600条轨迹作为训练集。图5为600条轨迹经过矢量化和归一化后的结果,从中可以看出,目标运动轨迹主要包含了左高右低、左低右高、中间高两边低3种情况。这3种轨迹对应着隐空间的3类特征,在仿真中给定K=3。图6为VAETP经过训练后从隐空间采样得到的120条轨迹,从中可以看出,VAE虽然能够生成和预测轨迹,但是相对于原始轨迹,3种运动特征之间的区别不明显,这是因为在VAE中,轨迹数据被视为从一个标准正态分布中采样得到。图7为GMVTP的生成预测结果,从中可以看出,3类轨迹之间区分更加明显,正是由于隐空间分布是混合高斯分布,因此能够更准确地描述轨迹特征。图8为随机选取的120轨迹使用GMVTP进行分类的结果,不同深线线条分别代表不同特征的轨迹,从中可以看出,GMVTP可基本实现轨迹的无监督分类。

图5 训练轨迹矢量集

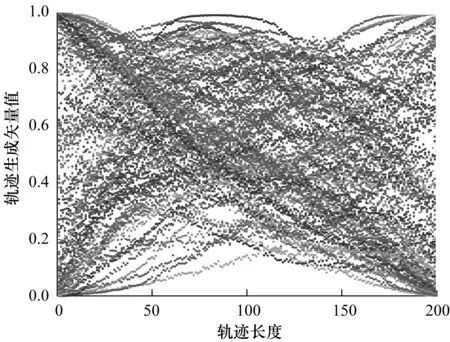
图6 VAETP算法的轨迹生成结果

图7 GMVTP算法的轨迹生成结果

图8 GMVTP算法的轨迹分类结果

3.3.2 算法性能比较

本节比较GMVTP和VAETP2种算法在相同训练集大小(800条轨迹)下的收敛性,迭代步数设置为300。图9为损失函数变化曲线。从中可以看出,VAETP在迭代150步左右收敛,而GMVTP在50步左右即收敛。损失函数值间接反映出生成轨迹与原始轨迹之间的差异性,由于GMVTP的隐空间结构被假设为混合高斯分布,在训练开始阶段就能够精确近似真实的分布,因此GMVTP的损失函数值始终小于VAETP并很快收敛。

图9 损失函数变化曲线

3.3.3 预测精度和时间比较

采用均方根误差(RMSE)计算轨迹预测误差:

图10 3种算法的预测误差比较

为比较3种算法的实时性,计算在相同收敛条件下不同训练集大小时算法的运行时间,实验结果取每种条件下训练30次的平均耗时,如图11所示。可以看出,GMMTP的平均训练耗时约为21 s,最长达到27 s,而VAETP和GMVTP两种算法的平均耗时在4 s左右。相对于GMMTP算法,后两种算法的训练耗时平均缩短了80.3%和74.9%,并且随着训练集的增大,GMMTP的训练时间显著增大,而VAETP和GMVTP两种算法的训练时间无明显增长。这是由于变分自编码器采用了随机梯度下降法更新网络参数,避免了GMMTP算法中有关概率分布期望的计算,同时TensorFlow框架下的GPU与程序之间的联系加速了网络参数的训练。因此,当轨迹数据集庞大时,基于VAE的轨迹预测算法优势更加明显。从图中还可以看出,GMVTP的训练时间略多于VAETP,这是由于GMVTP的网络结构更加复杂,导致训练时间略微增长,但从上文的仿真可知,GMVTP的预测误差相比于VAETP平均降低了35.59%,总体而言其性能优于VAETP。

图11 3种算法训练时间比较

综上所述,本文算法在预测精度和实时性上均优于传统的GMM轨迹预测算法,有利于实现舰船轨迹的在线预测,并且由于隐空间先验分布复杂度提高,该算法能够更精确地描述轨迹数据的特征,进一步减小预测误差。

4 结束语

海面舰船由于路径约束小,移动规律多变,且受到观测手段的影响,其轨迹数据特征较为复杂。为此,本文提出一种基于高斯混合-变分自编码器的轨迹预测算法GMVTP。将轨迹坐标转化为轨迹矢量,利用VAE提取轨迹特征并生成预测结果。针对海面舰船的轨迹数据特点,改进经典的VAE算法,将隐空间的先验分布假设为混合高斯分布,从而使其更符合真实的数据特征分布,并在隐空间中完成轨迹特征分类,实现端到端的轨迹预测。仿真结果表明,该算法在预测精度和实时性上优于传统的GMM模型,有利于舰船轨迹数据的在线训练与预测,并且提高了轨迹预测精度。下一步将考虑解决类别总数K的自适应问题以及各个类别概率向量π的训练问题。