单个固体颗粒促进薄液膜破裂的格子Boltzmann研究

刘学文，李金京，全晓军，熊伟

（上海交通大学机械与动力工程学院，工程热物理研究所，上海200240）

引 言

深入理解纳米或微米颗粒和泡沫之间的相互作用在很多领域有重要意义。在粉尘抑制领域，更好地理解粉尘颗粒与泡沫相互作用的基本原理是生产具有更高粉尘抑制性能的泡沫的关键[1]，对颗粒气泡或颗粒液膜相互作用的研究是胶体化学领域的研究热点[2-3]。此外，随着纳米流体在沸腾换热中的应用，纳米颗粒在沸腾现象中越来越重要[4-5]，核态沸腾中纳米颗粒会影响气泡稳定性进而影响沸腾换热，Quan等[6-7]和Binks等[8]关于纳米流体的沸腾实验中发现中等亲水性纳米颗粒可以吸附在气泡的气液界面上，因此可以减少气泡聚结从而提高沸腾换热性能。

当气泡接触另一个气泡或液体表面时，会形成液体薄膜，泡沫或气泡的稳定性与这些液膜的稳定性密切相关[9]。因此对单个纳米颗粒与薄液膜之间相互作用的研究是深入理解颗粒和泡沫之间的相互作用的基础，目前已经有很多文献从理论和实验方面对该现象进行了研究。

众多的研究表明[1,10-20]，对于两侧皆为气体的单层液膜，球形亲水性颗粒会增强液膜的稳定性，而球形疏水性颗粒会促进液膜的破裂。然而，目前大多数研究注重亲水颗粒对液膜稳定性增强的研究，针对疏水颗粒导致液膜破裂的研究极少。Frye 等[21]提出了一种针对单个颗粒与单层薄膜相互作用的理论模型，发现球形颗粒的接触角需要大于90°才能促进膜破裂，但是该模型中疏水颗粒初始时刻便位于液膜中间，这显然与实际不符。此外也有关于该现象的实验研究，Dippenaar[9]使用疏水玻璃球形微米颗粒对单个颗粒与单层薄液膜之间的相互作用进行了实验研究，结果表明接触角为102°的微米颗粒会促进液膜破裂，在一定程度上证实了理论预测的液膜破裂机制。Zhu 等[1]则在纳米尺度液膜上研究了单个球形玻璃颗粒与单层表面活性剂薄膜的相互作用，发现薄膜的寿命在加入亲水性颗粒后延长，在添加疏水性颗粒时减小。这些研究中，液膜厚度都远小于颗粒半径。对于理论模型，难以研究颗粒接触液膜并浸入液膜的过程，而实验研究中难以对颗粒接触角进行精确控制。

对于单个纳米或微米颗粒促进液膜破裂的现象，其时间空间尺度小，实验难以准确捕捉，单纯的理论与实验研究都不能直观展示颗粒与液膜相互作用的详细过程，在这方面模拟研究有其独特的优势。作为介观方法，格子Boltzmann方法（LBM）已被证明是研究润湿性对流体中固体颗粒运动影响的有效数值方法。Ladd[22-23]提出用于模拟固液悬浮液的2D 格子Boltzmann 模型，Joshi 等[24]改进Ladd 的模型[22-23]并与单组分/多相模型相结合，模拟悬浮在液体蒸气表面上的2D颗粒的运动。

本文通过将Joshi 等[24]的颗粒模型与Gong 等[25]的单组分/两相流模型结合，采用等温格子Boltzmann 方法两相流模型对单个颗粒与薄液膜之间的相互作用进行了研究，并对疏水颗粒促进液膜破裂的过程进行了详细研究。

1 格子Boltzmann方法

1.1 格子Boltzmann方法两相流模型

本文采用Gong 等[25]提出的Gong-Cheng 单组分/两相流模型。

格子Boltzmann 方法主要分为碰撞和迁移两个过程，采用BGK 碰撞算子的流体粒子分布函数的碰撞过程为：

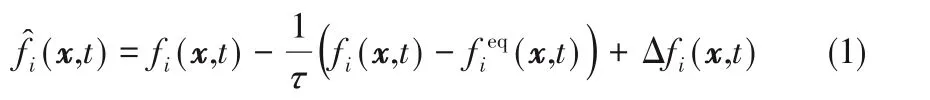
结合颗粒运动模型之后其迁移过程有所不同，具体迁移过程的方程可参考文献[26]，关于该二维两相流模型各项的具体设置可参考文献[25]。

1.2 颗粒运动模型

本文颗粒运动模型基于三个假设：(1)颗粒为球形，(2)忽略颗粒转动，(3)忽略布朗运动。根据牛顿第二定律，每个颗粒的运动可以通过以下方程式描述：

式中，Up是粒子的速度，Mp是颗粒的质量，二维情况下由式(3)给出：

式中,Rp是粒子的半径，ρp是粒子的密度，此处取为液体密度的1.5倍。

式（2）中的Fp是作用在粒子上的总作用力，由于本文只研究单个颗粒的行为且忽略重力的作用，因此总作用力包括来自周围流体的撞击力Fimp，附着力Fadh和动量交换力Fmom三部分，可以表示为：

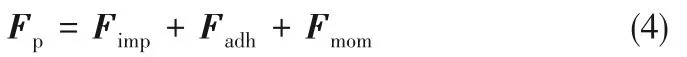
其中Fimp可参考文献[26]，Fadh是流体节点与粒子节点的相互作用力，表达式为[24]：

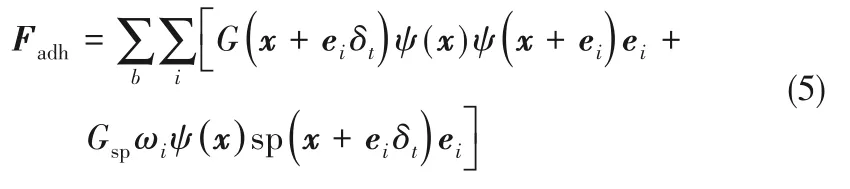
式中，b表示颗粒边界相邻的所有流体格点；Gsp是流固作用力强度系数，可用于调控颗粒表面润湿性；sp(x+eiδt)为指示函数，颗粒内部固体格点取1，流体格点取0。关于LBM 方法中固液接触角的更多计算可以参考文献[27]。关于Fmom的计算可参考文献[24]。

Gong-Cheng 模型相比普通单组分/多相模型具有更好的数值精度和数值稳定性[25,28]，将Gong-Cheng 单组分/两相流模型与颗粒运动模型相结合，固体颗粒单个时间步Δt（Δt=1）的位移为UpΔt，通过颗粒内部格点和流体格点的相互转化来实现颗粒位移。颗粒移动后，在t时刻由流体格点转化为颗粒内部格点的格点密度可直接取为ρp，而由固体颗粒内部格点转化为新流体格点的格点密度由周围流体格点的平均密度来表示[26]：

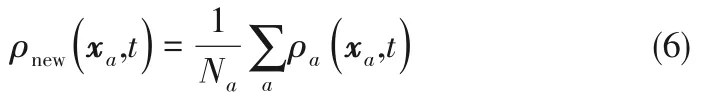
式中，xa表示新流体格点周围的流体点，Na表示周围流体点的数量，ρa表示xa位置处流体格点的密度。由式（6）即可得到新的流体格点的密度。

关于颗粒运动模型的更多细节可参考文献[24]。

2 颗粒亲疏水性

本节讨论在等温条件下单个颗粒漂浮在水面上的稳态情况，格子Boltzmann 方法中颗粒在水蒸气-水界面处的平衡位置取决于颗粒由于固液作用力引起的润湿性[29]，LBM 中通过调节系数Gsp可得到不同颗粒接触角。现在通过格子Boltzmann 方法(LBM)模拟单个粒子在无重力的情况下漂浮在液体表面的情况。图1(a)给出了格子单位为Nx×Ny =400 × 400 的计算域的2D 示意图，通过网格无关性测试[图1(b)]发现这一格子计算区域可以保证计算精度，高度为Ny/2的液态水充满下方区域，固体颗粒（半径Rp=20 个格子单位，实际单位约为30.6 nm）最初放置在气-液界面的中心，液体和水蒸气都处于饱和温度T0=0.85Tcr，在此温度下，液体和水蒸气的饱和密度分别约为6.63 和0.34。在x方向上施加周期性边界条件，并且在计算区域的顶部（y=400）和底部（y= 0）施加无滑移壁面边界条件。关于格子单位与实际物理单位转换可参考Wang 等[30]的方法，本文中1格子单位约对应1.53 nm。

接触角大于90°的疏水颗粒与接触角小于90°的亲水颗粒在液面不同位置如图1 中所示，作用于气-液界面处半径为Rp的球形颗粒上的界面力（Fi）可表示为[11]：

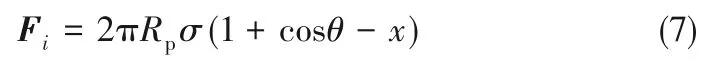
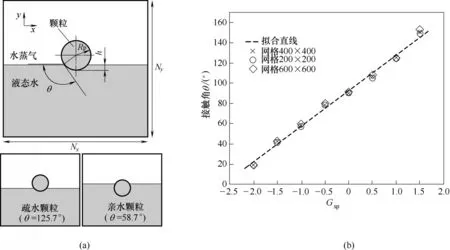
图1 液面上漂浮单个粒子的计算域示意图(a);不同网格数下Gsp与颗粒接触角关系图(b)Fig.1 Schematic of the computation domain for a single particle floating on liquid surface (a);Relationship between Gsp and contact angle with different grid numbers(b)

式中，σ为液体的表面张力，J/m2；θ为固体颗粒的接触角，(°)；x为颗粒浸入液体中的相对深度，等于其绝对浸入深度h与颗粒半径之比：x=h/Rp。如果Fi> 0，则向量Fi指向液相。在没有其他力的情况下，如果Fi= 0，则颗粒将在气-液界面处于平衡位置。此时可得颗粒平衡位置浸入液体深度为：

如式（8）所示，接触角唯一地确定了颗粒在液-气界面处的平衡位置。

3 结果与讨论

3.1 计算域设置

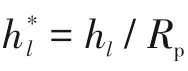
3.2 颗粒接触角对液膜破裂的影响

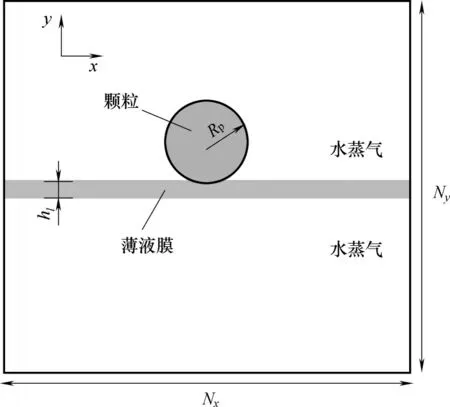
图2 单个固体颗粒与薄液膜相互作用的计算域示意图Fig.2 Schematic diagram of the computational domain simulating the interaction between a single solid particle and thin liquid film

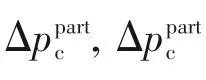
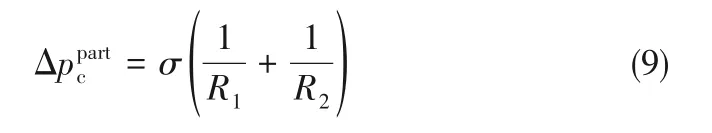
式中，R1和R2是描述颗粒附近弯曲的气-液界面的两个曲率半径，σ是水蒸气-水的表面张力。上下的气液界面会在该毛细力驱动下会沿着颗粒表面移动，当上下的气液界面接触时，颗粒与液膜接触极不稳定，液膜便会脱离颗粒表面而破裂[21]。

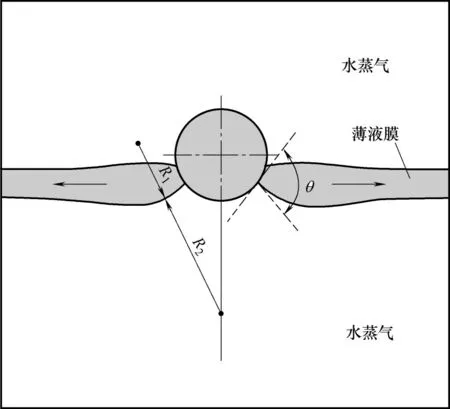
图3 液面弯曲产生毛细力示意图Fig.3 Schematic diagram of capillary force generated by liquid surface bending

模拟发现颗粒导致液膜破裂的整个过程如图4所示，液膜破裂现象与理论分析[32]和实验现象[9]基本一致。模拟发现疏水纳米颗粒导致液膜的破裂可以细分为两个阶段，阶段1 是颗粒接触液膜并在界面力（Fi）的作用下向液膜内部移动直至颗粒恰好接触下气液界面的过程，阶段2 是上下气液界面被毛细力驱动在颗粒表面移动的过程。

颗粒接触角越大，液膜在颗粒表面的弯曲程度越大，所产生的毛细力越大，液面线在颗粒表面移动的速度越大，上下气液界面会更快相遇从而导致液膜破裂，因此阶段2 时间大大缩短。但是颗粒接触角越大，由式（7）可知使颗粒向液体内部运动的界面力Fi越小，因此颗粒从接触液膜到接触液膜下界面的移动速度减小，而这却会导致阶段1 时间大大延长，阶段1 所耗费的时间远长于阶段2。图5 是不同接触角颗粒导致定厚度液膜破裂两个阶段的时间分布模拟结果，其中破裂时间为颗粒接触液膜直到液膜恰好脱离颗粒表面的时间间隔，图5表明，在颗粒接触角为106.7°附近时两个阶段综合耗费的时间最短，因此在此接触角附近颗粒导致液膜破裂时间最短。

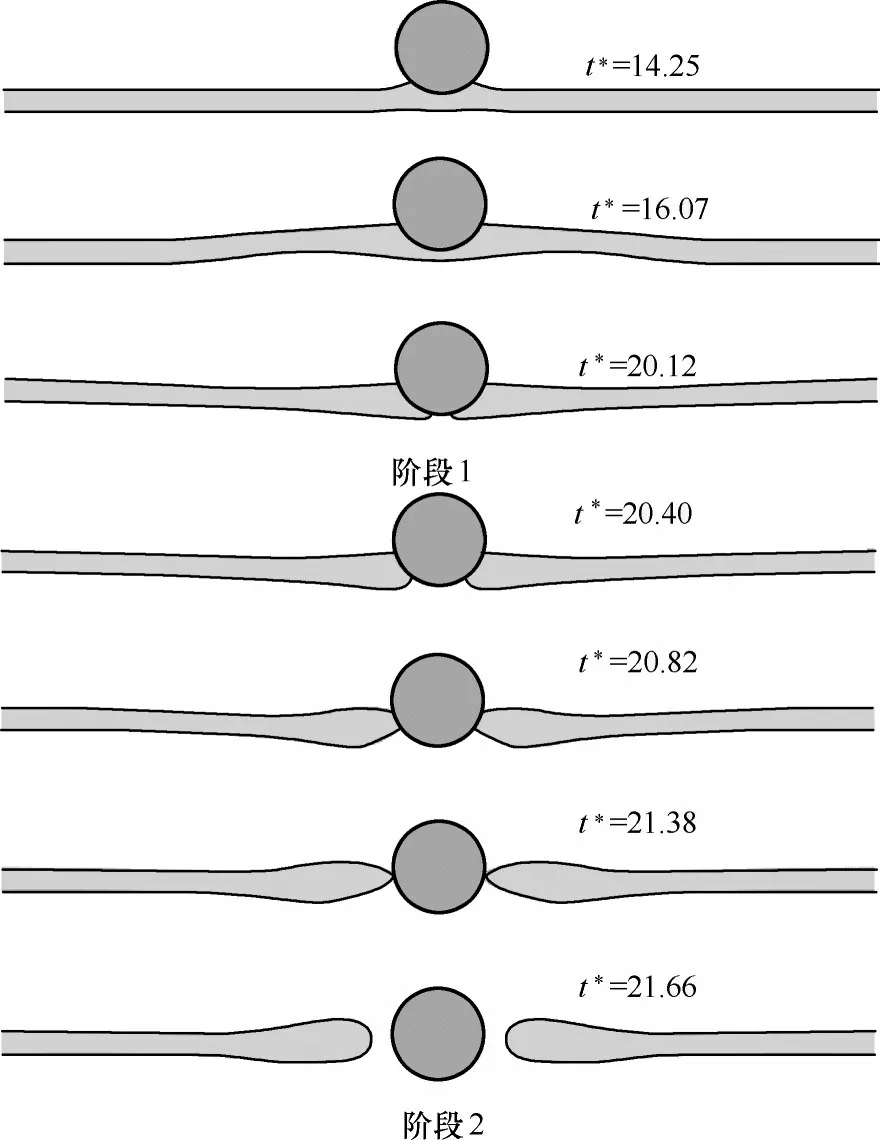
图4 球形疏水颗粒导致液膜破裂的两个阶段（接触角θ=106.7°，液膜厚度=0.4）Fig.4 Two stages of liquid film rupture caused by spherical hydrophobic particle(contact angle θ=106.7°,liquid film thickness=0.40)

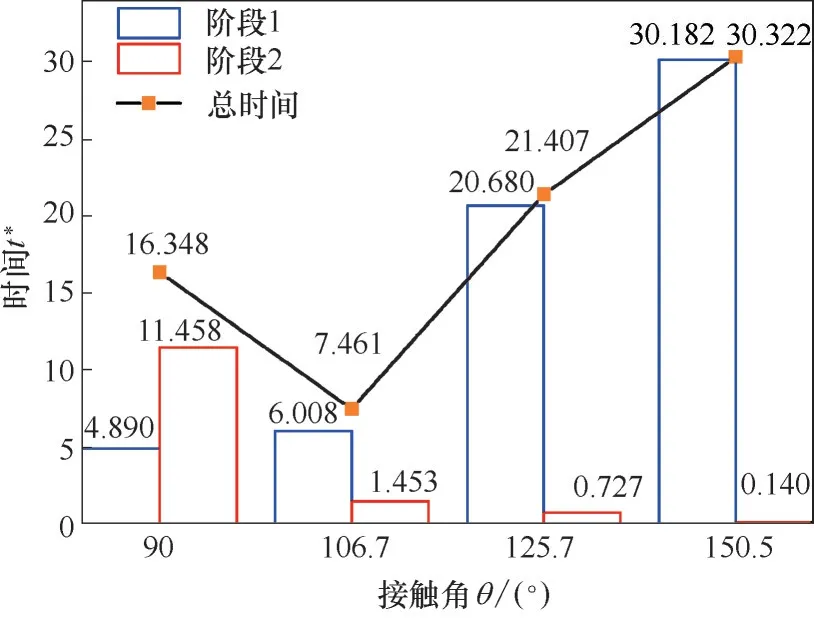
图5 不同接触角颗粒导致定厚度液膜破裂的两个阶段的时间分布(液膜厚度 =0.4)Fig.5 Time distribution of two stages of liquid film rupture caused by particle with different contact angle at a given thickness(liquid film thickness=0.4)

3.3 液膜厚度的影响

当颗粒接触液膜时，颗粒会在界面力的作用下向液膜内部移动，此时会有两种情况，一种是液膜的厚度小于颗粒在气液界面平衡时进入液体的深度，另一种是大于。

当第一种情况发生时，颗粒会在界面力的作用下直接穿透液膜并接触液膜下界面，然后开始图4所示的液膜破裂的第二个阶段。

第二种情况多发生于颗粒接触角过大即过于疏水的情况，此时界面力的作用不足以使颗粒穿透液膜并接触下界面，模拟结果如图6所示，此时颗粒下部液体不断向两侧排开，随着液体不断向两侧排开下液面则会不断向上移动，直到颗粒下部液面线接触颗粒，此后的现象与第一种情况相同。在这种情况下，前期颗粒排开液体向两侧运动的过程极为缓慢，因此颗粒导致液膜破裂的时间大大延长。

图6 展示的是当颗粒半径网格数为20、30 和40时导致液膜排水的示意图，液膜厚度均为=0.45，可见随颗粒半径网格数增加依然会出现排水现象，因此可以排除网格数量的影响。

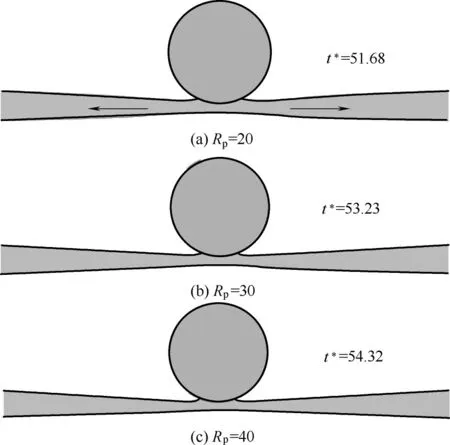
图6 疏水颗粒导致液膜排水示意图（接触角θ=150.5°，液膜厚度=0.45）Fig.6 Schematic diagram of liquid film drainage caused by particle(contact angle θ=150.5°,liquid film thickness=0.45)

图7是不同接触角颗粒导致不同厚度的液膜的破裂时间的模拟结果。对于接触角为90°和106°的颗粒而言，其平衡时进入液体的深度极大，并不会产生图6 的排水现象，因此液膜破裂时间随液膜厚度近似线性增长。对于接触角为125.7°的颗粒，当液膜厚度大于等于0.45 时，颗粒导致液膜破裂的时间大大延长，这是因为接触角为125.7°的颗粒平衡时能够浸入液体的深度为=1+cosθ=0.42，当液膜厚度大于0.42 时，颗粒仅依靠界面力无法穿透液膜，达到稳定的深度heq后(图6)，颗粒下部的液体不断向两侧排开，下方液相线逐渐靠近颗粒，直到接触颗粒表面，这个过程远远慢于颗粒依靠界面力运动的过程，因此耗费的时间呈现突然的增长。而对于接触角为150.5°和161.2°的颗粒而言，其能深入液膜的深度极小，因此在液膜厚度为0.13 的时候便已经是图6破裂机理，因此随液膜厚度增加，其导致液膜破裂的时间呈近似线性增长，并不会因为破裂模式的转变而导致破裂时间的突变。当液膜厚度为0.5 时，接触角为125.7°、150.5°以及161.2°的颗粒无法依靠界面力浸入液膜，因此会对液膜产生图6的排水现象，此时接触角越大排水越快，因此接触角161.2°的颗粒反而比125.7°和150.5°的颗粒更快导致液膜破裂。从图7 可以看出，当液膜厚度小于颗粒半径时，接触角为106.7°的疏水颗粒导致液膜破裂的时间总是最短。

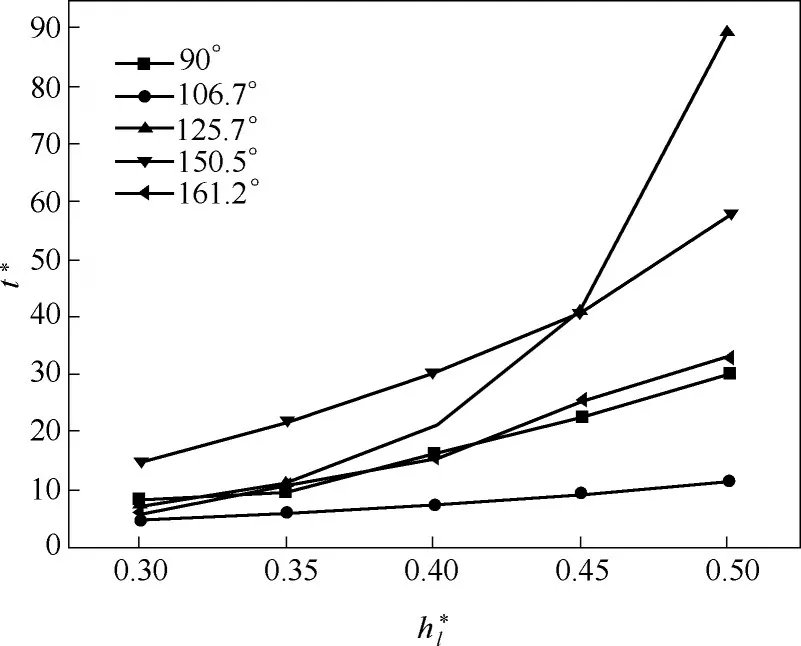
图7 液膜破裂时间与液膜厚度及颗粒接触角关系Fig.7 Time distribution of liquid film rupture of different thickness caused by particle with different contact angles

4 结 论

采用等温格子Boltzmann 方法两相流模型结合颗粒运动模型对单个颗粒导致液膜破裂的现象进行了数值模拟研究，得到如下结论。

（1）疏水性球形颗粒会导致液膜破裂，颗粒促进液膜破裂可以细分为两个阶段，一是颗粒接触液膜并在界面力的作用下向液膜内部移动直至颗粒恰好接触液膜下界面的阶段，二是上下气液界面在毛细力驱动下沿颗粒表面移动并接触的阶段。综合两个阶段的时间，发现颗粒接触角为106.7°附近时导致液膜破裂时间最短。

（2）液膜厚度与颗粒接触角的相对关系对液膜破裂时间有很大影响，当液膜的厚度大于颗粒在气-液界面平衡时浸入液体的深度时，此时界面力的作用不足以使颗粒穿透液膜并接触液膜下界面，液膜将会发生排水现象直至颗粒接触液膜下气液界面，在这种情况下，疏水颗粒导致液膜破裂的时间会延长。当不同接触角下均处于排水状态时，接触角越大则液膜排水越快。

由于缺少通用的理论分析与详细的实验数据，仅能对该现象进行模拟分析，模拟现象与理论和实验基本一致，但缺少定量对比，这将是下一步的研究重点。