浅谈多塔悬索桥初步设计分析方法
郭昊霖
(西南交通大学, 四川成都 610031)
与传统双塔三跨悬索桥相比,大跨度多塔悬索桥通过增设中塔,大大减小了主缆拉力,锚定数量和工程材料用量,拥有强大的跨越能力,成为跨越宽阔水域的理想桥型,拥有广阔的应用前景[1]。大跨度多塔悬索桥在有诸多优点的同时,也面临许多难题与挑战。由于中塔缺乏边跨主缆的有效约束,该结构体系的竖向刚度不足,在最不利荷载工况下,主梁会产生较大的挠度而影响其使用性能。采用刚性中塔能在一定程度上改善上述问题,但是会导致中塔塔顶承受过大的不平衡力,引起主缆与中塔塔顶鞍座的抗滑移安全性等问题[2-3]。当前针对每一座大跨度多塔悬索桥,在整体设计参数确定后,均就鞍座的抗滑移安全性问题展开进一步的理论和试验研究,以保证鞍座的抗滑移安全性满足设计需求。以上所述的设计流程繁复,桎梏了大跨度多塔悬索桥的发展与应用。
针对传统大跨度多塔悬索桥,提出一种可以同时考虑整体上结构体系主要设计参数对于结构刚度的影响和局部上鞍座摩擦抗力是否满足整体设计需求的理论分析模型,以指导其初步设计,无疑将有利于这类桥型的发展与应用。
1 结构变形求解
对于三塔悬索桥,最不利加载工况为一个主跨满布荷载,其余跨空载,如图1所示,此时中塔鞍座两端的不平衡索力达到最大值,加劲梁和缆索的变形也达到最大值。
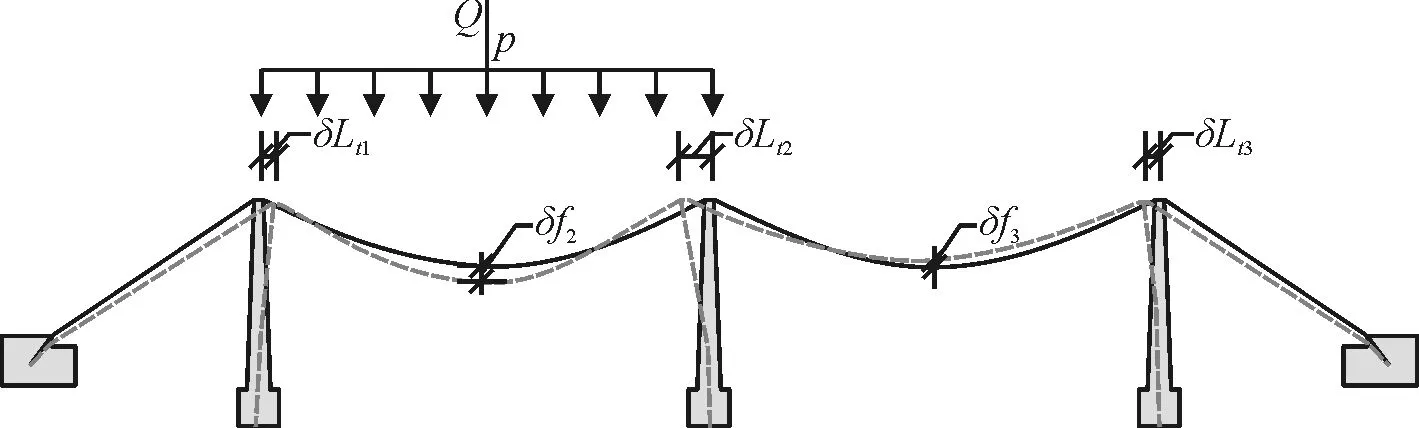
图1 三塔悬索桥最不利荷载工况下变形示意
本文在分析三塔悬索桥的受力特性时,采用以下假定:(1)采用全漂浮体系,加劲梁恒载由主缆承担,恒载沿跨长为均布荷载,在恒载作用下的主缆线形为抛物线;(2)忽略吊杆的重量和弹性伸缩,即荷载作用下,同一跨内主缆与加劲梁的竖向变形相同;(3)边塔由于边缆强大的纵向约束,活载下边塔顶的位移约等于零。基于以上假定,可将传统三塔悬索桥结构等效为弹簧模型,如图2所示。
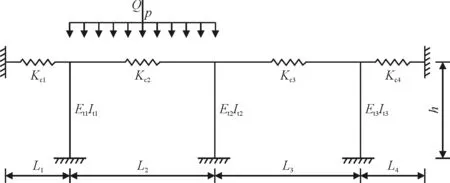
图2 三塔悬索桥等效弹簧模型
图中,Kci为第i号缆索的等效弹簧刚度,EtiIti为第i号桥塔的抗弯刚度,Li为第i跨跨长,h为桥塔高度。
1.1 中跨主缆水平刚度
主跨主缆变形示意图如图3所示。
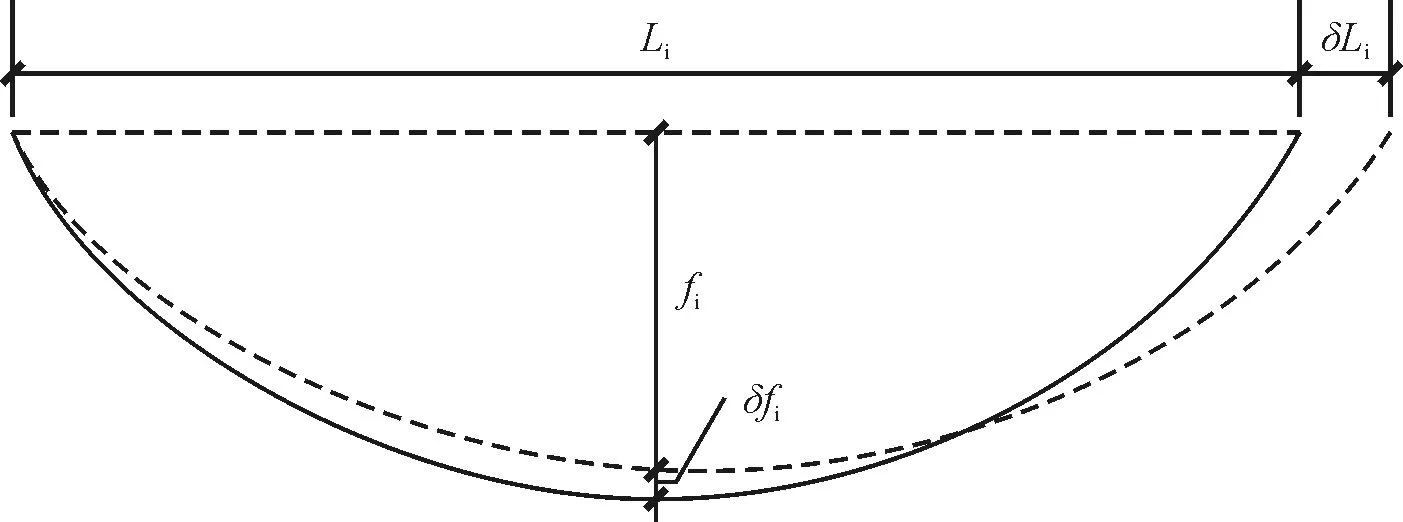
图3 中跨主缆变形示意
恒载作用下,中跨主缆的水平力为:
(1)
式中:w为主缆所承受的每延米恒载重量,Li为第i跨长度,fi为第i跨主缆垂度。发生变形时,主缆水平力为:
(2)
联立式(1)和式(2),略去高阶项得:
δHi=Hiδfi/fi+2HiδLi/Li
(3)
又主缆垂度改变与水平位移的关系为[4]:
(4)
联立式(1)、式(3)~式(4)得中跨主缆水平刚度为:
(5)
1.2 结构位移求解
由均布荷载p产生的主缆拉力为:
(6)
由集中荷载Q产生的主缆拉力为[5]:
(7)
根据图2所示等效弹簧模型,由中塔水平方向受力平衡可得:
(8)
活载作用下加载跨的主缆和加劲梁的竖向挠度由两部分组成,第一部分为主缆水平位移δLi引起的竖向位移δfdi,可由式(4)计算;第二部分为不考虑主缆水平位移时活载p和Q引起的竖向位移。其中,活载p引起的竖向位移为[6]:
(9)
活载Q引起的竖向位移为[5]:
(10)
活载作用下非加载跨的主缆和加劲梁的竖向挠度仅由主缆水平位移δLi引起的竖向位移δfdi一部分组成,综上所述,活载作用下加载跨和非加载的竖向挠度分别为:
参试品种(系)播量均为525万粒/hm2,但是通过田间考种结果表明:最终产量较高的品种(系)保苗数均较高,甘啤6号保苗474万株/hm2,居所有参试品种(系)第二位;垦啤6号保苗552万株/hm2,居所有参试品种(系)第一位;产量最低的甘啤4号保苗321万株/hm2,居所有参试品种(系)第七位。试验结果表明:不同品种对春旱的抗性不同造成单位面积保苗数差异显著,最终导致产量结果与单位面积保苗数成正相关关系。
δf2=δfd2+δfp2+δfQ2
(11)
(12)
其中,加载跨第2 跨表现为下挠,非加载跨第3跨表现为上拱。
2 主缆拉力求解
中塔塔顶鞍座的受力示意图如图4所示,其中,θ2为第2跨主缆在中塔塔顶处与水平方向的夹角,θ3为第3跨主缆在中塔塔顶处与水平方向的夹角,α为中塔塔顶处主缆与鞍座的包角,T2为第2跨在中塔塔顶处的缆索拉力,H2′为恒载和活载共同作用下第2跨在中塔塔顶处的水平缆索拉力,T3为第3跨在中塔塔顶处的缆索拉力,H3′为恒载和活载共同作用下第3跨在中塔塔顶处的水平缆索拉力。

图4 中塔塔顶鞍座受力示意
中跨主缆在恒载作用下的主缆线形为:
(13)
对式(1-13)求导并令x=Li得中塔塔顶处主缆与水平方向的夹角的正切值为:
(14)
由式(14)可得:
(15)
(16)
(17)
(18)
得到中塔塔顶两端主缆的拉力T2和T3后,代入JTG/TD65-05-2015《公路悬索桥设计规范》中规定的主缆与鞍座间的抗滑移安全系数K的计算式[7]:
(19)
式中:α为主缆在鞍槽上的包角(rad),μ为主缆与鞍座槽底或隔板间的摩擦因数,规范建议值为0.15。规范要求,当K≥2时,主缆与鞍座之间的抗滑移性能满足要求。
3 模型验证
参考泰州长江大桥的设计参数,将原设计中的半漂浮体系改为全漂浮体系,其余主要设计参数不变;将各项数据代入本章所述的初步设计理论模型当中,并在MIDAS/Civil中建立该桥的有限元计算模型,将初步设计理论模型所得的各项解与有限元模型所得的各项解进行对比,分析误差,验证初步设计理论模型的正确性与可靠性。泰州长江大桥的结构立面图如图5所示,主要设计参数如表1所示。

图5 泰州长江大桥结构立面(单位:m)

图6 泰州长江大桥有限元模型示意
活载的取值根据JTGD60-2015《公路桥涵设计通用规范》[8],均布荷载p采用32.2kN/m,集中荷载Q采用1 104.8kN。在MIDAS/Civil中建立的有限元模型示意图如图6所示,其中主缆和吊杆由只受拉桁架单元模拟,加劲梁和桥塔由梁单元模拟,模型中只受拉桁架单元共计636个,梁单元共计270个。由初步设计理论模型和有限元模型得到的结构位移、缆索拉力和主缆与鞍座之间的抗滑移安全系数值如表2所示。
从表2中可以看出,初步设计理论模型得到的解与有限元得到的解吻合良好,有效验证了初步设计理论模型的正确性和可靠性,该理论模型可应用于未建大跨三塔悬索桥的初步设计过程。根据泰州长江大桥的实际工程背景资料,设计时采用式(19)对主缆与鞍座之间的抗滑移性能进行评估时,得到的抗滑移安全系数K值不能满足规范要求。通过试验数据测得主缆与鞍座之间实际的界面摩擦系数为0.2,故在计算K值时将μ取为0.2进行主缆与鞍座之间的抗滑移安全性能评估。从表3-2可以看出当μ取为0.2时得到的抗滑移安全系数K值略大于规范要求的限值2,在实际工程建造时,还在鞍座内的主缆索股之间增设了两道竖向摩擦板,以增加主缆与鞍座之间的摩擦力,从而保证结构具有足够的抗滑移安全性能。
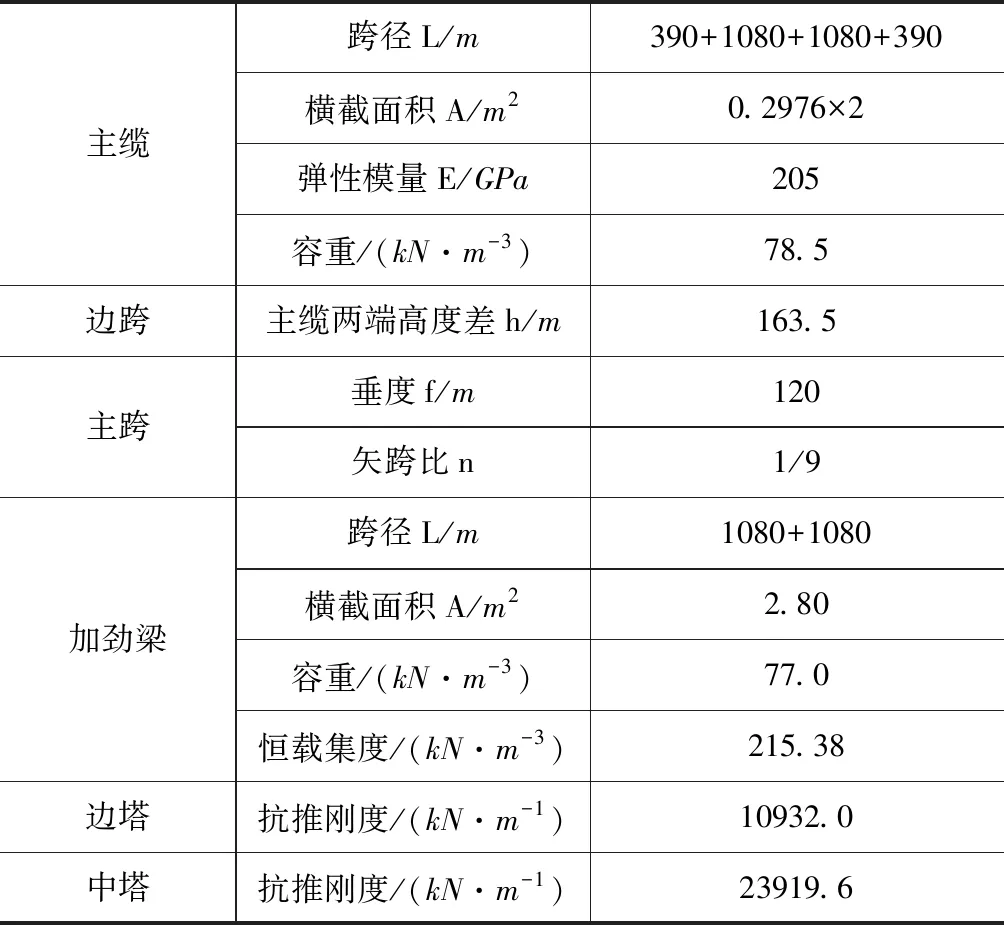
表1 泰州长江大桥主要设计参数

表2 理论模型解与有限元模型解对比
4 结论
(1)三塔悬索桥的受力模型可简化为等效弹簧模型,通过对主缆水平刚度的求解,可以求得最不利荷载工况作用下的主缆和加劲梁变形以及中塔塔顶两端的主缆拉力,将得到的结构位移解和主缆拉力解用于三塔悬索桥的初步设计过程,可以简便快捷地对结构进行验算,判断其是否满足变形要求和主缆与鞍座之间的抗滑移性能要求。将理论模型用于初步设计过程,可以显著提升初步设计的效率。
(2)通过本文所提出的初步设计理论模型所得到的解与有限元得到的解吻合良好,有效验证了初步设计理论模型的正确性和可靠性,说明该理论模型可应用于未建大跨三塔悬索桥的初步设计过程。
(3)当用规范所要求的抗滑移安全系数计算公式对多塔悬索桥主缆与鞍座之间的抗滑移性能进行评估时,若计算得到的抗滑移安全系数K值不能满足要求,可根据实际工程所采用的主缆和鞍座结构,通过试验测定主缆与鞍座之间实际的界面摩擦系数,再进行抗滑移安全性能验算。由于规范所建议的摩擦系数值0.15为所有实测值的下限,该取值过于保守,实际工程中所测得的摩擦系数往往高于0.15,使得主缆与鞍座之间的抗滑移性能进而满足要求。若使用实际测得的摩擦系数进行验算仍不能满足主缆与鞍座之间的抗滑移性能要求,则可通过在鞍座内的主缆索股之间增设竖向摩擦板来增加主缆与鞍座之间的摩擦抗力。

