基于Android的PDR改进算法研究

刘玲玉，刘狄松，常铁原

(河北大学 电子信息工程学院，河北 保定 071000)

0 引言

自从1992年剑桥大学的Active Badge提出采用红外传感技术开发的室内定位系统以来，室内定位技术取得了很大的发展。如采用Wi-Fi[1]、蓝牙、ZigBee、超声 波[2]、超宽 带[3](UWB)、RFID[4]、惯性 导航等技术[5]实现的室内定位系统也相继出现，但是至今还没有一款普遍适用的室内定位产品出现，为此相关学者与研究机构都在努力完善室内定位技术这一局限。近年来由于智能手机技术的进步与普及，基于Android的室内定位也成为了一个焦点，本文利用智能手机内置的传感器(如加速度传感器、磁场传感器)来实现PDR算法，进而实现室内定位，同时，为了提高PDR算法的定位精度，对PDR算法做了优化，主要采用卡尔曼滤波和粒子滤波算法，以及本文提出的直线判定这一方法。

1 PDR算法

PDR算法的实现主要包括三部分，即步数检测、步长检测、航向检测。本文采用改进的峰值检测法来进行步数检测，采用步长的经验模型来进行步长检测，航向检测则采用Android提供的方法进行获取。具体算法如下：

(1)步数检测

行人在行走过程中其自身的加速度具有周期性[6]，因此，可以根据这一特性进行步数检测。本文实际测试的行走过程中手持的智能手机的三轴合加速度在7.5～12.5 m/s2之间，实际编程时为了获取充足的样本数据将算法中的合加速的的筛选阈值设定为[g，3g](其中 g=9.81 m/s2)，同时为了减少因身体抖动带来的伪波峰的影响，设定峰值之间的时间间隔要满足[0.4 s，1 s](之所以设定为该区间，是因为行人的步频通常为 1～2.5 Hz)。智能手机采集三轴合加速度样本数据只有满足上述两个条件，才会判定为一步，这也是本文提出的改进的峰值检测法的主要思想。

(2)步长检测

本文采用线性步长模型进行步长检测，算法表达式如式(1)所示：

其中，l表示步长，单位：m；k、e 为回归参数；Accmax、Accmin分别为单步周期内的行人加速度最大值与最小值(本文指智能手机三轴合加速度的最值)，单位：m/s2。

通过多次试验采集行走过程中加速度最值与实际步长均值的样本数据，再通过MATLAB软件线性拟合确定式(1)中的参数 k、e，本文最终的步长检测模型如式(2)所示：

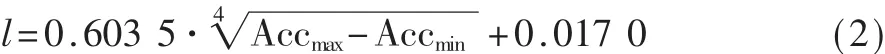
(3)航向检测

本文的PDR算法是基于智能手机进行开发的，而智能手机中具有多种传感器能够实现航向的检测。之前智能手机中具有单独的方向传感器，如今已使用加速度传感器与磁场传感器替代。并且Android提供了封装好的方法用来计算手机的方向角度，如本文采用Android提供的getRotationMatrix()和getOrientation()方法来计算手机顶端与正北方向的夹角。

2 改进的PDR算法

使用PDR算法实现定位时除了其本身产生的累积误差外，行走过程中产生的波动或者身体的抖动也会对最终的定位结果产生影响。本文为了提高PDR算法的精度和稳定性，提出了两种优化方案，第一种是通过直线判定的方式来平滑航向数据；第二种方案是使用滤波算法对步长数据和结果进行优化。接下来对这两种方案进行详细阐述：

方案一：直线判定

在同一水平面内，人们行走过程中的轨迹大致可分为沿直线行走和曲线行走，其中轨迹为直线时行人的行走状态相对比较稳定，本文针对这一点对行人的行走轨迹进行判定，如果为直线行走，则对相邻的航向进行平滑处理，目的是为了减少由于行走过程中身体的抖动对航向带来的影响，进而使得直线行走时的航向趋于稳定。直线判定的实现步骤如下：

通过实际测试，得知在沿直线行走时（手持手机于胸前，且手机顶端指向前进的方向），手机检测到的相邻航向数据之间差值的绝对值不超过15°，因此，如果相邻的两个航向数据之间的差值的绝对值小于等于15°，那么采用式(3)对航行数据进行平滑处理，否则，轨迹为曲线，保持航向数据不变。

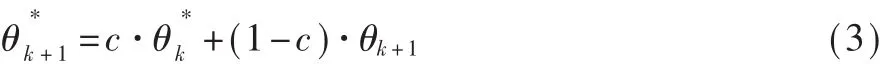
采用上一步中的阈值进行判定时，可能存在突变数据，该突变数据超过了阈值的范围，但是它又不属于曲线行走时的航向，为了排除该类数据所带来的影响，需要对判定为非直线行走的航向数据进一步筛选，筛选算法如下：

如果θk被判定为非直线行走时的航向，那么计算 θk+1与 θk-1之间的差值的绝对值，若该绝对值小于等于 15，那么 θk为突变数据，并且令 θk=θk-1。

方案二：滤波优化

方案一主要针对行走轨迹以直线为主的情形，但实际情况中还有以曲线为主的轨迹，而方案一不适用于该情况。因此，本文提出了滤波优化的方案，主要是针对行走时的步长数据和估算结果进行优化，进而提高PDR算法在轨迹为以曲线为主时的定位精度。采用卡尔曼滤波算法平滑处理步长数据，粒子滤波算法对结果进行优化。

本文将卡尔曼滤波进行了一定的简化，即令A=B=H=1，U(k)=W(k)=0，Q=0.000 001，R=0.001，同时令X(0)=0，P(0)=1.0，那么公式相关表达式的形式变为：

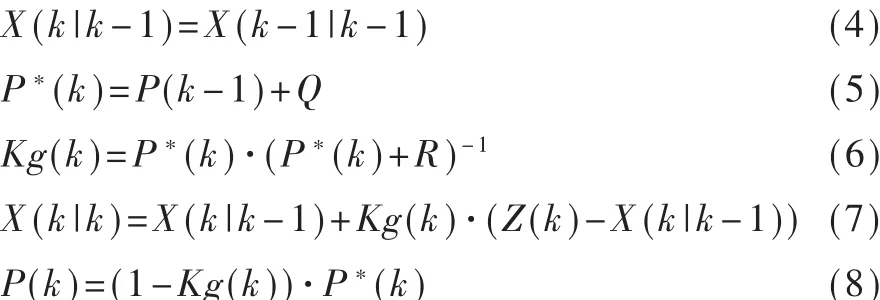
其中，X(k|k-1)表示第k-1时刻对第k时刻的状态的预测值；X(k-1|k-1)表示第k-1时刻修正过的状态的估计值；P(k)表示第k时刻状态估计值与真实值的协方差；P*(k)表示第k时刻状态预测值与真实值的协方差；Kg(k)表示第k时刻的卡尔曼增益参数；X(k|k)表示第k的状态估计值。

通过式(4)～式(8)对步长数据平滑处理，再通过平滑后的步长数据估算行人的位置坐标。

粒子滤波优化的基本思想是：首先，以前一个PDR估算的位置为中心，在半径为 radius(单位：m)的范围内以任意的角度生成N个点，这N个点称之为粒子，将它们的初始权重设置为1/N，接着这些粒子按下一个位置的步长和航向运动，最后将运动后的粒子群中的粒子与PDR的估算的下一个位置进行比较，并按欧式距离的大小更新粒子的权重，所有粒子的位置坐标的加权和即为最终的优化结果。

本文结果优化是在步长优化后的基础上进行的，相关的算法模型如式（9）～式（15）所示。

粒子初始化方程：

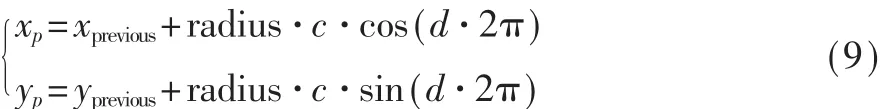
其中，(xp，yp)表示某一个粒子的位置坐标；(xprevious，yprevious)表示PDR估算的行人的前一个位置的坐标；radius表示半径，为一个常数；c、d表示随机生成随机数，本文取0到1之间的浮点型数值。

粒子运动方程：

其中，(xlater，ylater)表示运动后的粒子位置坐标；llater表示PDR检测的下一个位置处的步长；θlater表示PDR检测的下一个位置处的航向。

权重更新方程：

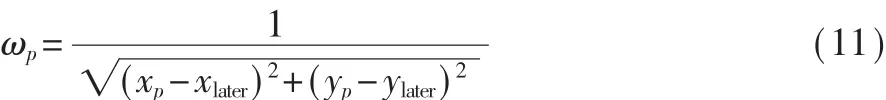
其中，ωp表示更新后的粒子权重；(xlater，ylater)表示 PDR估算的行人下一个位置的坐标。

归一化处理：

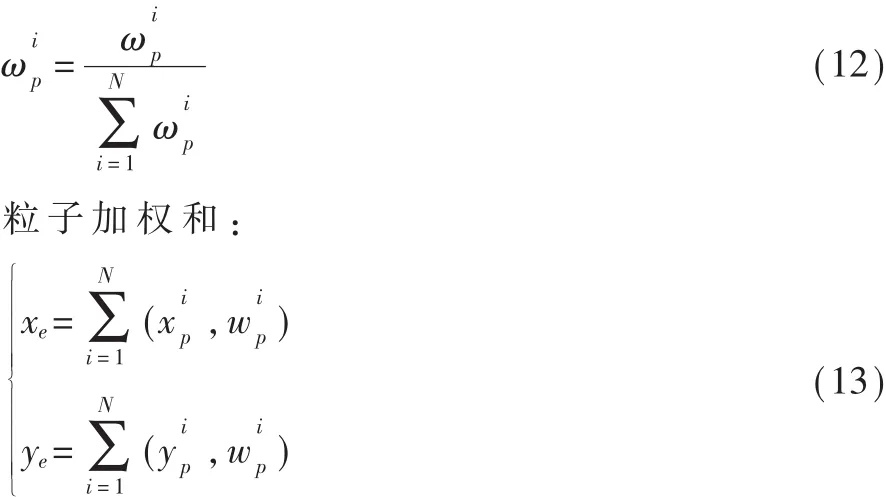
其中，(xe，ye)表示粒子加权后的位置坐标；N表示粒子的个数；()表示第 i个粒子的位置坐标；ωip表示第i个粒子的权重。

重采样：本文所得的最终优化的结果是经过多次迭代后的均值，每次迭代为一次粒子滤波过程，同时产生一个加权和，即如果总共进行n次迭代，那么将产生 n个加权和(由式(13)计算所得)，将这 n个加权和的平均值作为最终的优化结果。但是为了保证每次迭代后的结果的多样性，需要对粒子群中的N个粒子进行更新，即重采样。本文采用如下方法实现重采样，主要思想是：对于粒子群中的N个粒子，经过一次迭代后，其权重根据与PDR估算的位置坐标的距离进行更新，如式(11)所示，再通过式(12)、式(13)获得一个加权和，之后需要对粒子进行更新(也叫重采样)，为下一次迭代做准备。重采样的数学相关表达式如式(14)～式(16)所示：

初始时，令num=0，r=N(N表示粒子的个数)

其中，ranges(0)=0，ranges(mid)表示从第 1个粒子到第mid个粒子的权重之和；e为随机生成的一个浮点型数据，且 e∈(0，1)。

按式(14)～式(16)实现二分法，直到 num+1≥r，此时将第num个粒子根据式(9)进行重采样，并将它的权重设置为1/N。如此循环N次，即可完成粒子的重采样。

3 实验与分析

为了测试算法的效果，本文选定河北大学工商学院的C2楼的第三层的走廊为实验测试的场所，主要分为两种场景进行测试：直线为主的轨迹和曲线为主的轨迹。两种轨迹的初始位置坐标都设置为(0，0)，其中粒子滤波的迭代次数设置为 70次，半径radius=3 m，粒子数N=200。两种场景的测试轨迹图分别如图1和图2所示。

从图1中可知采用直线判定平滑的估计轨迹在轨迹的直线部分更加接近实际轨迹，并且直线判定平滑后，轨迹误差从2.46 m降低为0.64 m；从图 2可知，采用卡尔曼滤波平滑处理步长数据和粒子滤波优化结果同样能够使得估算轨迹更加接近实际轨迹，其中PDR算法的估算轨迹误差为6.20 m，采用卡尔曼滤波平滑处理步长数据后的误差降为1.67 m，在卡尔曼滤波的基础上采用粒子滤波优化结果的轨迹误差降为1.08 m。本文的误差采用公式（17）计算所得：

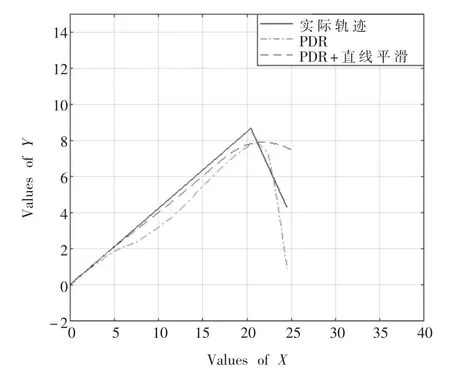
图1 直线为主的轨迹

图2 曲线为主的轨迹

其中，(x，y)表示定位坐标，(x0，y0)表示实际坐标。

4 结论

本文提出的针对两种场景 (直线为主的轨迹、曲线为主的轨迹)下的优化方案能够提高PDR算法的精度，具有一定的使用价值。但是PDR算法所得结果都是相对的，即需要一个初始的参考位置，在实际应用中需要加以解决。如与基于Wi-Fi或者蓝牙的指纹法相结合，指纹法能够提供初始的参考位置或者校准PDR算法的累积误差。除此外，还可以与其他技术相结合进行融合定位，如地图匹配、滤波融合等，这也是之后的一些可供参考的研究方向。