基于时域法和频域法的车身动态疲劳分析

谢敏捷 ， 赵 松 ， 曾小利 ， 邵 建

（长安汽车汽车股份有限公司汽车工程研究总院，重庆 401133）

0 引言

针对结构的疲劳破坏问题，传统工程界往往采用静态疲劳分析方法进行分析[1]。通过计算单位载荷下结构的静态应力，乘以车身受到的实际载荷，计算随时间变化的应力曲线，基于Miner 线性累积损伤理论，用雨流法进行损伤的求解。然而，汽车在实际的行驶环境中，存在着复杂的振动激励，传统的准静态分析由于无法考虑结构动态特性的影响[2]，损伤计算并不准确，难以识别风险位置。因此，考虑结构动态特性的影响，对车身进行动态疲劳分析具有重要意义。

动态疲劳分析中主要有时域法和频域法两种计算方法[3]。时域法通常能得到比较准确的累积损伤分析精度，并可以处理非平稳高斯随机过程，但涉及较大的累积损伤计算工作量；频域法可以大幅度减少计算量，并提供更完备的响应信息，但其准确性易受载荷历程特征的影响[4-9]。

本研究基于某车型的TB 车身数据和VPG 仿真载荷谱数据，分别用时域法和频域法开展车身动态疲劳分析研究，其中，以时域法分析结果为基准，对比两种方法的结果一致性和计算效率，验证频域法在车身疲劳计算中的有效性，为动态疲劳技术在工程中的应用奠定一定基础。

1 动态疲劳分析基本原理

1.1 模态叠加法理论基础

车身时域法动态疲劳分析基于模态叠加法进行，通过对运动方程解耦可以大幅度提升分析效率。振动响应的物理坐标可转换为模态坐标表示：

可转换为：

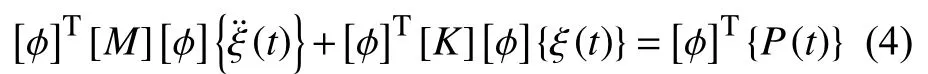
1.2 频域法寿命理论基础

频域法动态疲劳分析中，通过概率密度函数（PDF）实现结构损伤的求解。随机振动疲劳理论中，Dirlik 公式应用较广，其计算PDF 的公式为：

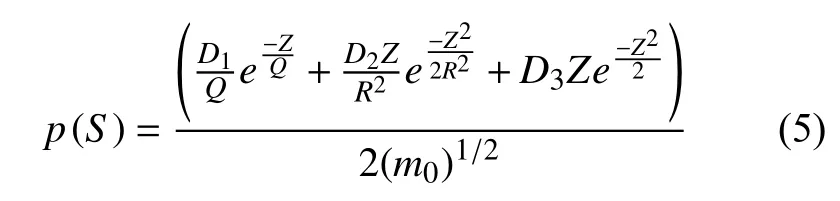
其中：

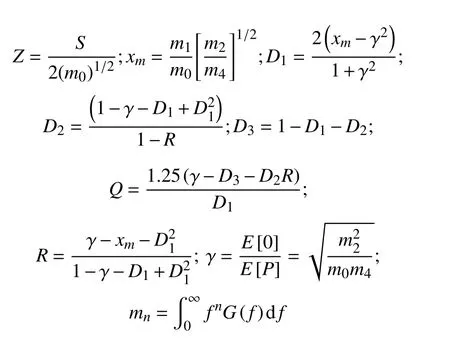
式中， G( f)为响应的应力功率谱密度函数（PSD）。

根据PDF 函数求解应力幅值为 S时对应的循环次数：

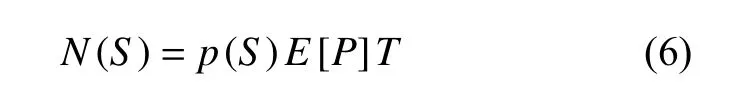
车身动态疲劳分析的流程如图1 所示。时域法动态疲劳分析中，通过模态瞬态分析求解得到车身的模态应力及各工况下的模态坐标，叠加之后计算得到结构各工况下的动应力曲线，结合材料的应变-寿命曲线（E-N 曲线），根据Miner 线性累积损伤理论计算结构的损伤值；频域法动态疲劳分析中，由载荷PSD 及结构传递函数计算结构的应力响应PSD，通过Dirlik 随机载荷模型求解结构应力幅值PDF，由Miner 线性累积损伤理论计算得到结构的损伤值[10]。

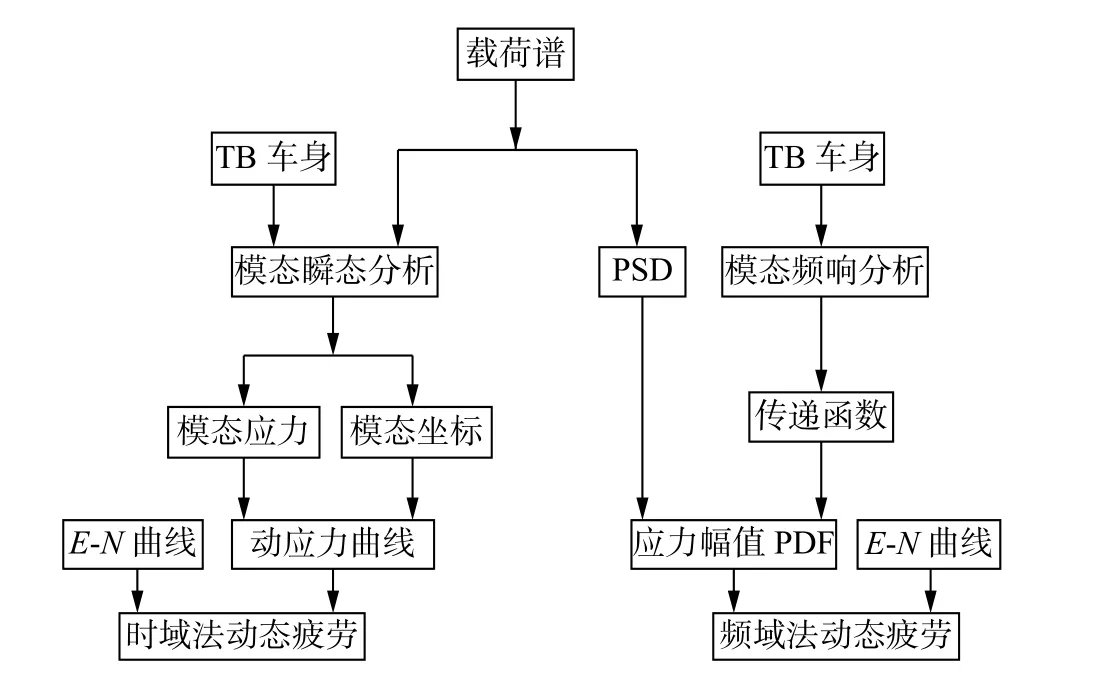
图1 车身动态疲劳分析流程图Fig.1 Process of dynamic fatigue analysis of trimmed body

2 车身动态疲劳有限元模型建立

用Hypermesh 对某车型TB 车身进行网格划分，简化车身上的圆孔、倒角等特征，焊点采用ACM 实体建模形式进行建模，划分完成的有限元模型如图2 所示。建模完成后，节点数为1 911 473，模型单元总数为2 180 354，其中，三角形单元总数为74 210，占全体单元的3.4%，三角形单元总数在5%以内，符合规定要求。本次分析关注的对象为白车身，除去座椅、车门等无关区域后，计算疲劳时模型单元的总数为988 141。

图2 某车型有限元模型Fig.2 Finite element model of a vehicle

为验证有限元模型的精度，以该模型为对象进行模态分析，并将分析结果与模态试验结果对标。表1 为车身主要模态的对标结果，结果显示，车身主要模态分析频率与试验频率的误差均在7%以内，表明该有限元模型能够满足分析精度要求，可以进行后续分析。

接附点载荷是通过VPG 仿真获取的。首先，通过3D 激光扫描技术获取试验场的数字路面模型，通过轮胎动力学台架测试和参数辨识生成适用于耐久载荷分析的FTire 轮胎模型，然后基于样车的整车参数建立整车多体模型，最后集成路面、轮胎、多体模型进行VPG 仿真和车身载荷提取。图3a 为整车多体动力学模型行驶通过虚拟路面的路面特征，图3b 为该整车模型的右前轮胎轧过路沿时各轮胎的受力情况。

表1 某车型车身模态对标Table 1 Comparison of analytic modal and experimental modal

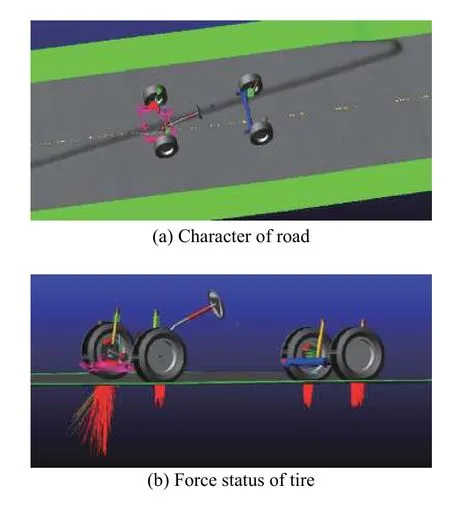
图3 整车多体模型VPG 仿真过程Fig.3 VPG simulation on multi-body dynamical model

3 车身动态疲劳分析及结果讨论

根据金属材料疲劳试验的国家标准[11]，对车身所用典型材料进行测试，得到应变幅、应力幅和失效循环数等数据，对试验数据进行回归分析可以得到不同材料的E-N 曲线，并建立材料数据库。

使用时域法计算车身动态疲劳时，在NASTRAN 中通过模态瞬态分析求取车身的模态应力和模态坐标，计算中，截断模态、阻尼比等可按工程经验给定以保证求解精度。将模态瞬态分析求解得到的模态应力和模态坐标输入nCode，导入实测的材料E-N 数据库进行疲劳计算。

使用频域法计算车身动态疲劳时，计算的关键在于将接附点的时域载荷数据转换为PSD。本研究分析的车身接附点较多，在车身上分布较广，如果计算PSD 时只考虑各通道的自谱，由于相位信息的丢失，将会对分析结果产生极大的误差。因此，考虑到求解的精确性，生成的PSD 矩阵中包含了各通道的自谱和互谱[12]。出于数据平稳性的考虑，在进行傅立叶变换前对时域载荷进行截取，剔除载荷曲线中的变化幅值较小的区域，以使生成的PSD 更符合实际路面特征。载荷的时频域转换通过快速傅立叶变换（FFT）实现，图4 为某路面工况下，车身某接附点X、Y、Z3 个方向载荷时频域自谱的转换，其中，图4a 为载荷的原始数据，图4b为剔除小幅值区域后的载荷数据，图4c 为图4b 中数据转换得到的该路面PSD，PSD 显示该路面载荷的频率成分集中在20 Hz 以内，对车身的低阶模态将产生较大的激励作用。

在NASTRAN 中通过模态频响分析计算车身的传递函数，截止频率、阻尼比的设置与时域法分析中的设置相同。通过传递函数和各工况PSD，基于Dirlik 公式可以在频域中计算结构的疲劳寿命。

3.1 损伤结果对比

车身疲劳动态分析共包含37 个工况，图5 为所有工况叠加后车身时频域疲劳分析结果云图。

图5 显示，不同分析方法的分析结果中，损伤值超过0.1 的区域均集中于后排座椅安装区域，热点单元分布基本一致。为进一步对比时频域的分析结果，绘制如图6 所示车身时频域损伤数值对比散点图，在对比损伤数值时，数值对比在0.5～2.0 之间表示一致性较好。以时域法分析中损伤数值排前1000 的单元为参考，剔除三角单元67 个，以及与RBE2 或RBE3 单元相连的单元207 个，这些单元由于单元类型和单元的连接方式会对计算结果造成影响，在本分析中不予考察。剩余的726 个单元中，294 个单元频域损伤计算值小于时域损伤计算值，432 个单元大于时域损伤计算值。此外，566 个单元损伤数值对比在0.5～2.0 之间，占考察单元总数的78.0%。

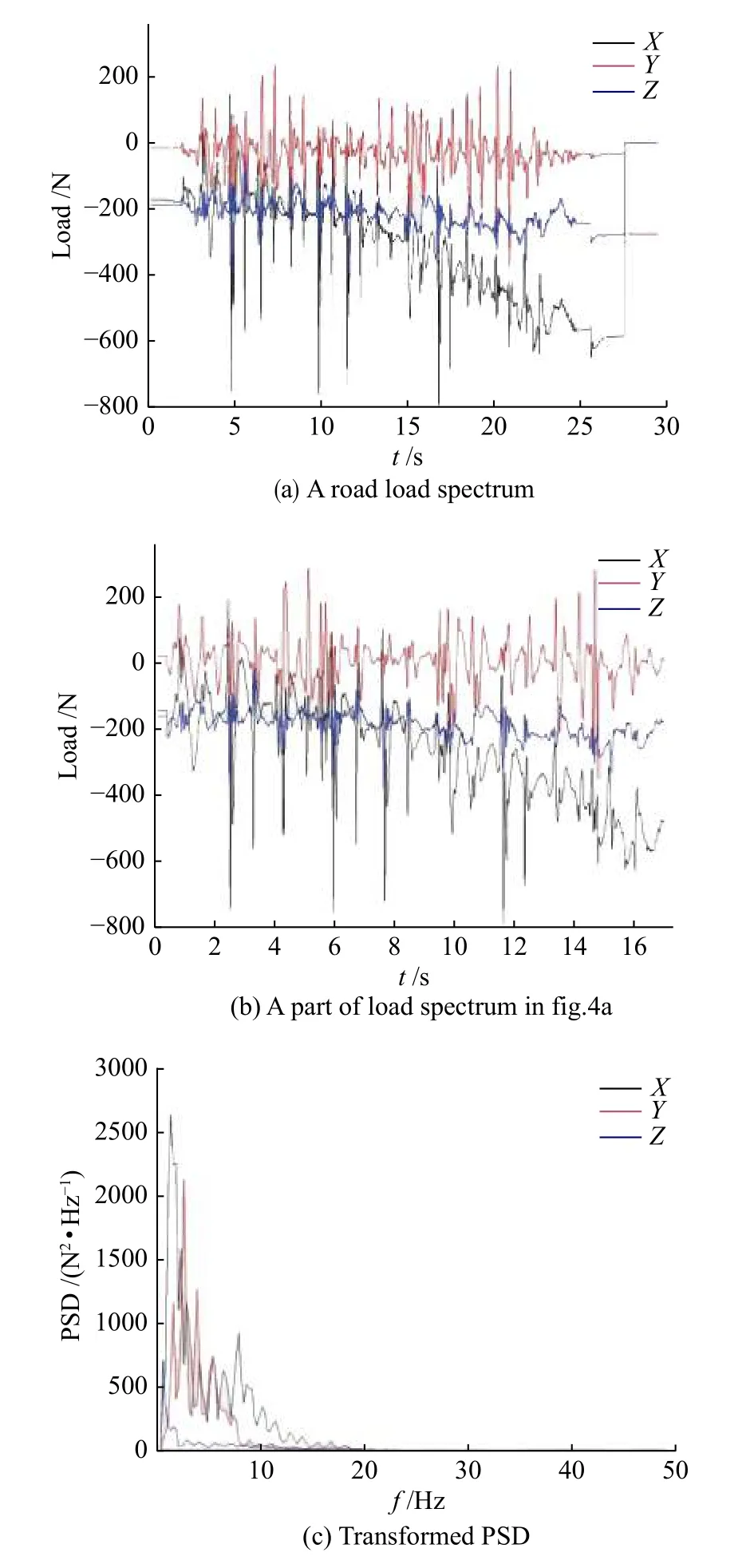
图4 某路面载荷谱和PSDFig.4 A road load spectrum and transformed PSD

图5 车身损伤计算结果Fig.5 Fatigue analysis results of trimmed body

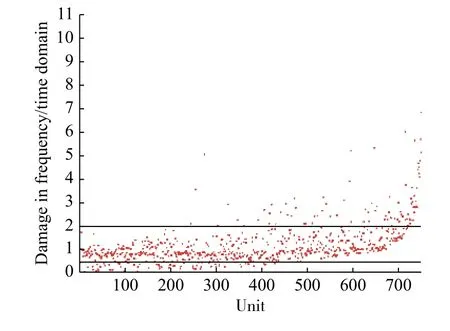
图6 车身时频域损伤数值对比散点图Fig.6 Scatter of fatigue damage ratio between frequency domain method and time domain method for trimmed body

对损伤值最高的单元进行考察，在计算的37 个工况中，有2 个工况对该单元损伤的贡献最大，时域下2 个工况的损伤值占全路面损伤的89.8%。对2 个工况下损伤数值大的前1000 个单元进行考察，去除三角单元和与RBE2、RBE3 连接的单元，剩余单元中2 个工况下时频域对比值在0.5～2.0 间的单元分别占考察单元总数的68.5%和80.1%。损伤占比高的工况下时频域对比值在可接受范围内，可以认为用频域法分析车身疲劳具有可行性。

3.2 计算效率对比

使用频域法分析可以大幅度提升工程中的分析效率。时域法计算中，由于涉及37 个工况，模态瞬态响应分析共耗时43.5 h，nCode 计算疲劳总计耗时20 h，整个流程耗时63.5 h；频域法计算中，模态频响分析耗时9 h， CFV 计算单元损伤耗时2.5 h，总计约11.5 h，相比之下，使用频域法分析车身疲劳效率显著提升了82%。

4 结论

1）频域法分析得到的热点单元与时域法基本一致，关注的损伤较大的单元中，78.0%的单元损伤时频域对比值在0.5～2.0 之间，且损伤占比大的工况下数值对比合理，均在可接受范围内。

2）与时域法相比，使用频域法大幅度提高了计算效率。因此，在项目设计初期，可以用频域法分析确定热点区域，从而引导产品设计，在项目中后期则用时域法分析单元和焊点的损伤。