轻骨料无腹筋混凝土梁剪切破坏及尺寸效应:细观模拟
金 浏,蒋轩昂,杜修力
(北京工业大学城市减灾与防灾防护教育部重点实验室,北京 100124)
轻骨料混凝土由于其质轻、高耐久性、高保温性等优点已被广泛应用于桥梁工程及高层建筑等混凝土工程结构[1]。同时,轻骨料混凝土亦存在弹性模量低,脆性明显,且易发生剪切破坏等特点。因此,需对轻骨料混凝土构件的抗剪性能开展研究。
钢筋混凝土梁是由钢筋和混凝土组成的复杂构件,是土木工程结构中常见的受剪构件之一。剪切破坏是钢筋混凝土构件失效模式中最危险的一类,通常表现出强烈的脆性特征,因而可能表现明显的尺寸效应行为。
针对普通骨料混凝土梁,研究者对无腹筋混凝土梁的剪切破坏机制及尺寸效应开展了大量的研究。如:Kani[2]设计了截面高度为150 mm~1220 mm 的几何相似的无腹筋钢筋混凝土梁的抗剪试验,研究发现,梁截面的有效高度对梁的受剪承载力有较大的影响,具有明显的尺寸效应。Nojiri 等[3]和Shioya 等[4]通过均布荷载作用下的钢筋混凝土梁的试验发现,随着截面尺寸增加梁的受剪承载力会有较大的降低。Bažant 等[5]进行了一系列有效截面高度为25.4 mm~406.4 mm 的无腹筋简支梁受剪试验,验证了此范围内简支梁剪切破坏的尺寸效应。Tan 等[6]对大尺度钢筋混凝土梁进行了深入的研究,他们认为钢筋混凝土梁斜裂缝的开裂强度与梁的尺寸无关,但极限承载时的抗剪强度则存在非常明显的尺寸效应。Chana[7]设计了截面高度为150 mm~750 mm 的36 根钢筋混凝土简支梁的抗剪试验,亦证实了尺寸效应的存在。Kim 和Park[8]对最大梁深为1000 mm 的不同剪跨比(1.5~6)的高强钢筋混凝土无腹筋梁开展抗剪破坏试验,发现高强混凝土梁剪切强度尺寸效应与普通混凝土类似,且尺寸效应与腹筋率无关。另外,于磊等[9]、车轶和于磊[10]以及Zararis 和Papadakis[11]试验结果表明:无腹筋钢筋混凝土梁的抗剪强度存在明显的尺寸效应。Sherwood 等[12]关于薄板剪切破坏试验的研究发现最大骨料尺寸对剪切承载力有重要影响;Sherwood[13]进行了无腹筋钢筋混凝土梁抗剪试验,发现有效高度从280 mm 增大到1400 mm 时,梁的名义剪切强度下降了43%。总体而言,上述研究工作均证实了无腹筋混凝土梁剪切破坏存在明显的尺寸效应。
近年来,也有研究者开始关注轻骨料混凝土梁抗剪性能,如:吴涛等[14]开展了高强轻骨料混凝土深受弯构件受剪性能的试验工作,发现剪跨比显著影响构件的极限承载力。在此试验基础上,刘喜等[15]建立了基于软化拉-压杆模型计算理论的高强轻骨料混凝土深受弯构件受剪承载力计算模型。最近,易伟建等[16]对不同骨料种类的无腹筋梁受剪性能开展了试验工作,发现:相比于普通骨料混凝土梁,轻骨料混凝土梁的剪切破坏面更为光滑,承载力更低。总体而言,这些研究工作促进了对轻骨料混凝土梁,尤其是无腹筋混凝土梁受剪破坏及力学性能的认识。尽管如此,对轻骨料混凝土梁剪切破坏行为还缺乏系统性的研究,对其破坏机理的认识还远远不足,更少见关于其剪切破坏尺寸效应方面的研究报道。
本文将轻骨料无腹筋混凝土梁作为研究对象,研究其剪切破坏行为及抗剪强度的尺寸效应规律,并揭示其与普通骨料混凝土梁受剪性能的差异。鉴于此,建立了无腹筋混凝土梁剪切破坏行为及尺寸效应研究的三维细观数值分析模型与方法。在与已有试验结果吻合良好的基础上,研究了不同尺寸普通及轻骨料无腹筋混凝土悬臂梁在单调加载下的剪切破坏模式与失效机制,揭示了名义剪切强度的尺寸效应规律。
1 轻骨料混凝土梁三维细观模型
1.1 三维几何模型的建立
混凝土尺寸效应源于其微-细观组成的非均质性[17-19]。为揭示轻骨料无腹筋混凝土梁剪切破坏行为及尺寸效应规律,这里采用细观尺度模拟方法来进行研究。从细观尺度来看,混凝土可以被视为一种三相复合材料,包含骨料、融合了细骨料的硬化水泥砂浆基质,以及骨料与桨体粘结处的界面过渡区[19-21]。目前,国内外研究者已提出了众多细观模拟方法来生成非均质混凝土试件,如陈永强等[22]采用格形化方法(Lattice)和统计技术建立了三维非均匀材料的有限元模型;Caballero等[23]和Lopez 等[24]基于界面元法对混凝土试件的拉伸断裂行为进行了模拟分析;梁正召等[25]、党发宁等[26]、马怀发等[27]均在混凝土断裂破坏的三维数值模拟方面做了研究工作。其中,随机骨料模型被证明是一种有效的模拟混凝土破坏过程和变形的细观力学方法,在混凝土断裂力学中有广泛的应用[28-29]。本文参考文献[19-21],将粗骨料(普通及轻质)颗粒假定为球体,混凝土采用二级配(粗骨料最小等效粒径为12 mm,最大等效粒径为30 mm),骨料体积分数约为30%,通过Monte Carlo 随机投放的方法将粗骨料颗粒投放到砂浆基质中,并将粗骨料周围1 mm 的薄层设定为界面过渡区,进而生成素混凝土材料的三维细观尺度分析模型。在生成的素混凝土试件基础上插入钢筋笼,进而生成非均质的钢筋混凝土悬臂梁三维细观数值模型,典型的几何模型如图1 所示。
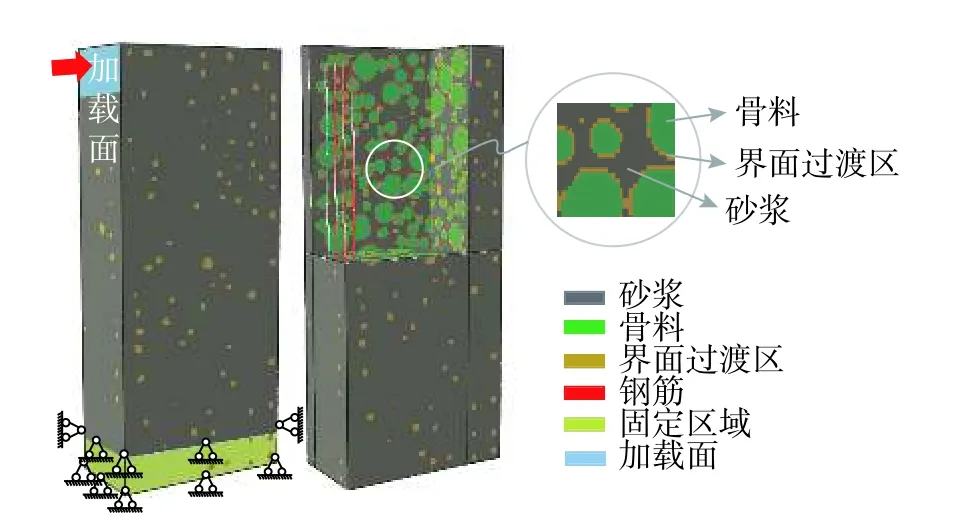
图1 无腹筋悬臂梁三维细观数值模型及加载示意图Fig. 1 3D meso-scale numerical model of concrete cantileverbeams without web reinforcement and sketch map
混凝土部分(骨料、砂浆基质及界面过渡区)采用六面体三维实体单元进行划分,梁中纵筋采用梁单元进行离散。综合计算量和计算精度的考量,以及下文中对3 个不同网格尺寸(1 mm、2 mm、4 mm)破坏模式及计算结果的比较,选取的网格单元平均尺寸为2 mm。采用如图1 所示的位移控制继续加载,旨在获得整个试件的全过程变形特性。借助ABAQUS 有限元软件,采用Newton-Raphson 法进行非线性分析计算。
1.2 细观组分及粘结-滑移本构关系


1.3 细观数值模型的验证
参照易伟健等[16]的简支梁试验,选用LB-2.2-1.58 与B-2.2-1.58 试验组,LB 表示轻骨料混凝土试验梁,B 表示普通骨料混凝土试验梁,剪跨比为2.2,配筋率为1.58%,简支梁尺寸为200 mm×400 mm×2000 mm。试件中,混凝土设计强度等级为C40 和LC40。实际通过18 个边长为150 mm的立方体试块测得轻骨料混凝土和普通混凝土立方体试块的抗压强度分别为43.9 MPa 和42.1 MPa。
如图4 无腹筋简支梁三维细观数值模型及加载示意图,网格尺寸为4 mm。因本文建立的模型为细观模型,基于细观层次的骨料颗粒、砂浆基质及两者之间的界面过渡区的三相复合材料参数的确定如表1 和表2。需要说明的是,表1 砂浆基质力学参数取自试验[16]中的实测数据,用“*”号标记;骨料的力学参数取自试验[20],用“**”号标记;而对于界面过渡区的力学参数的确定而言,通过反演法获得。

图4 无腹筋简支梁三维细观数值模型及加载示意图Fig. 4 3D meso-scale numerical model of concrete simply supported beams without web reinforcement and sketch map

表1 普通混凝土试件细观组分及钢筋力学参数Table 1 Mechanical parameters of meso components of normal concrete specimens and reinforcing bars utilized
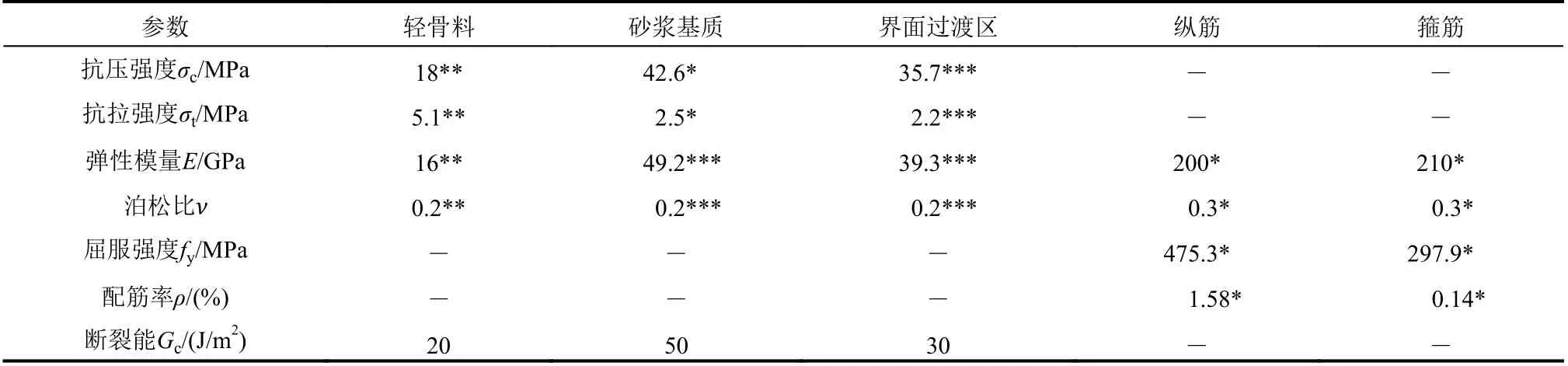
表2 轻骨料混凝土试件细观组分及钢筋力学参数Table 2 Mechanical parameters of meso components of lightweight aggregate concrete specimens and reinforcing bars utilized
数值模拟中,通过反复试算并且与试验结果对比来获得某些材料参数,是一种重要且科学的研究方法。具体做法是:将实际的砂浆基质的力学参数进行不同程度的折减(如70%~85%),作为界面力学参数的试算值,然后对混凝土立方体试块(边长为150 mm)进行反复的压缩破坏数值模拟试验,选取最接近实测混凝土抗压强度的一组数据作为界面力学参数。当采用表1 中给出的界面参数(用“***”号标记)时,获得的普通混凝土抗压强度为42.4 MPa,与实测值42.1 MPa 非常接近,因此可以认为采用该组力学参数是合理的。
表2 中砂浆基质力学参数取自试验[16]中的实测数据,用“*”号标记;轻骨料的力学参数取自试验[32],用“**”号标记;界面过渡区的力学参数则通过反演法获得。具体做法同上,当采用表1和表2 中给出的界面参数(用“***”号标记)时,获得的轻骨料混凝土试件抗压强度为44.1 MPa,与实测值43.9 MPa 较为接近,因此可以认为采用该组力学参数是合理的。
借鉴Bažant 等[18]的数值模拟验证方式,本文基于表1 和2 中所示的力学参数开展了不同网格尺寸(网格1 表示1 mm;网格2 表示2 mm;网格3 表示4 mm)普通混凝土梁与轻骨料混凝土梁抗剪破坏的三维细观数值模拟,获得了如图5 所示的试验结果[16]与模拟结果破坏模式对比图,以及如图6 所示的简支梁中部集中P-Δ(荷载-位移)关系曲线对比图。从图5 可以看出,无论是普通混凝土试件轻骨料混凝土试件,本文的细观模拟破坏模式均与易伟健等[16]的试验结果吻合良好,且网格大小对破坏模式的影响不显著。另外,图6 中模拟得到的荷载-位移关系亦与试验结果吻合良好。
2 轻骨料混凝土梁剪切破坏分析

图5 模拟与试验破坏模式的对比Fig. 5 Comparison of failure modes obtained by meso-scale simulations and experimental tests
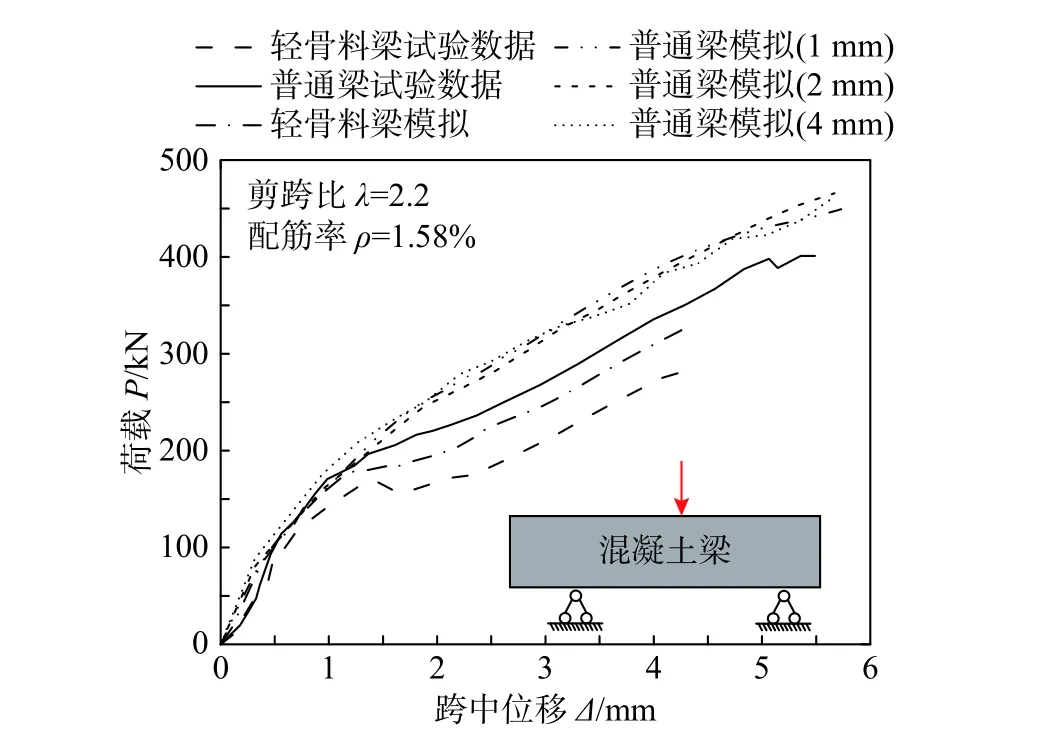
图6 细观模拟与试验荷载-跨中位移曲线的对比Fig. 6 Comparison of the P-Δ curves by meso-scale simulations and experimental tests
本节借助上述验证的三维细观数值模拟方法,拟对不同几何尺寸相似的普通及轻骨料混凝土悬臂梁的剪切破坏行为进行模拟与分析。鉴于此,对如表3 所示的4 种不同尺寸的无腹筋混凝土悬臂梁破坏行为进行研究。表3 中,给出了混凝土悬臂梁的名称,横截面尺寸(b×h),纵筋保护层厚度c,截面有效高度h0,剪跨比λ,梁长l 及纵筋率ρ。需要说明的是,试件名称栏NW(normal weight)表示普通骨料,LW(light weight)表示轻骨料,数字“1、2、3、4”表示不断增大的横截面尺寸;各试件剪跨比λ 均为2,纵筋配筋率为1.6%。为了消除一定的偶然性,每种试件方案模拟3 次(即具有3 组不同的骨料分布)。
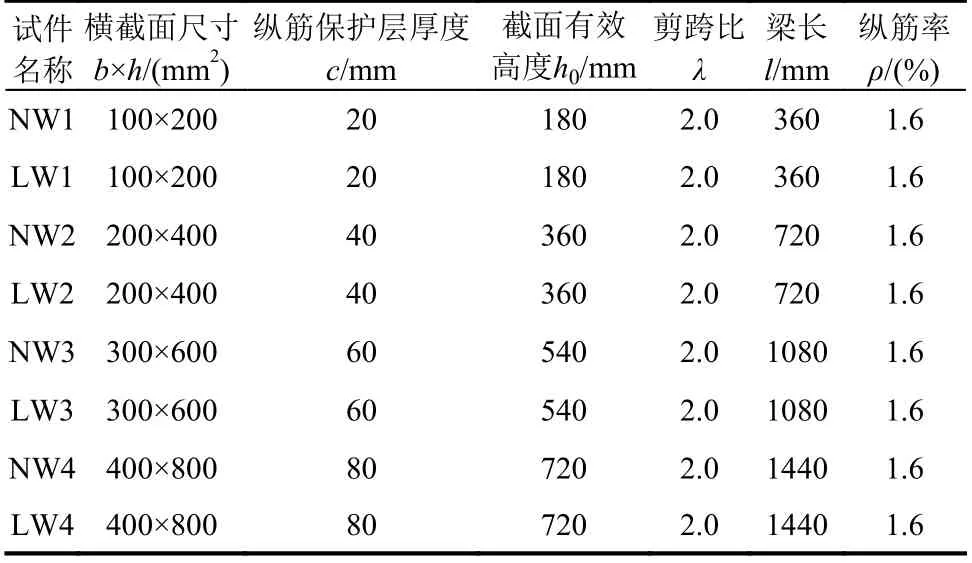
表3 混凝土悬臂梁几何参数Table 3 Geometrical parameters of concrete cantilever beams


3 剪切破坏尺寸效应
3.1 破坏模式
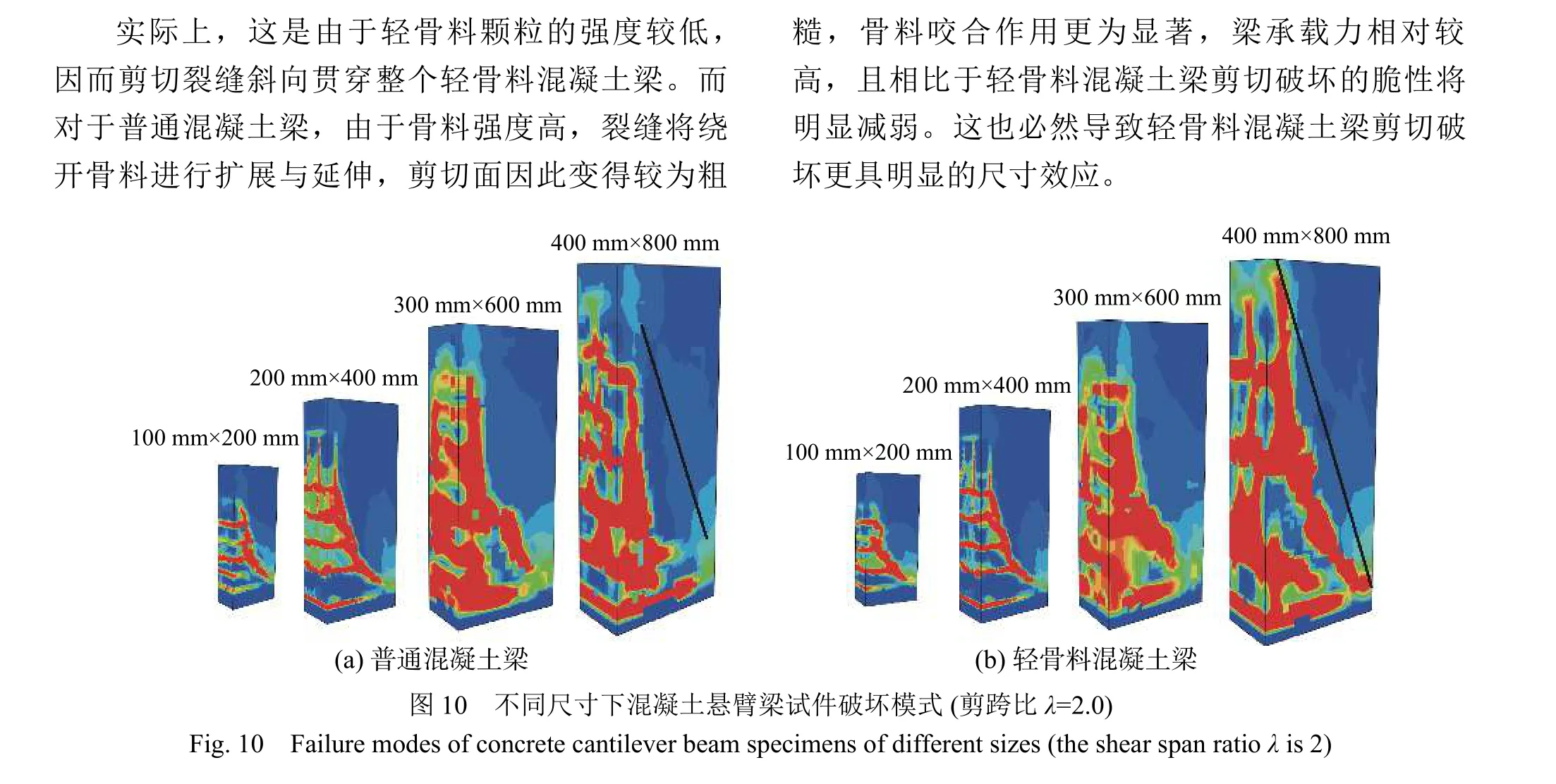
不同尺寸(梁高为200 mm~800 mm)下普通与轻骨料混凝土悬臂梁(剪跨比λ=2)的最终破坏形态分别如图10(a)和图10(b)所示。可以看出,无论是轻骨料还是普通骨料混凝土梁,试件均发生明显的剪切脆性破坏;不同尺寸下的轻骨料混凝土梁与普通混凝土梁的破坏模式基本一致,最终均形成由加载点到固定端底部的贯通斜裂缝导致整个结构失效。
3.2 荷载-位移关系
图11 是本文建立的不同尺寸下普通(NW)与轻骨料(LW)混凝土悬臂梁细观尺度力学分析数值模型在位移加载下得到的荷载-位移曲线。
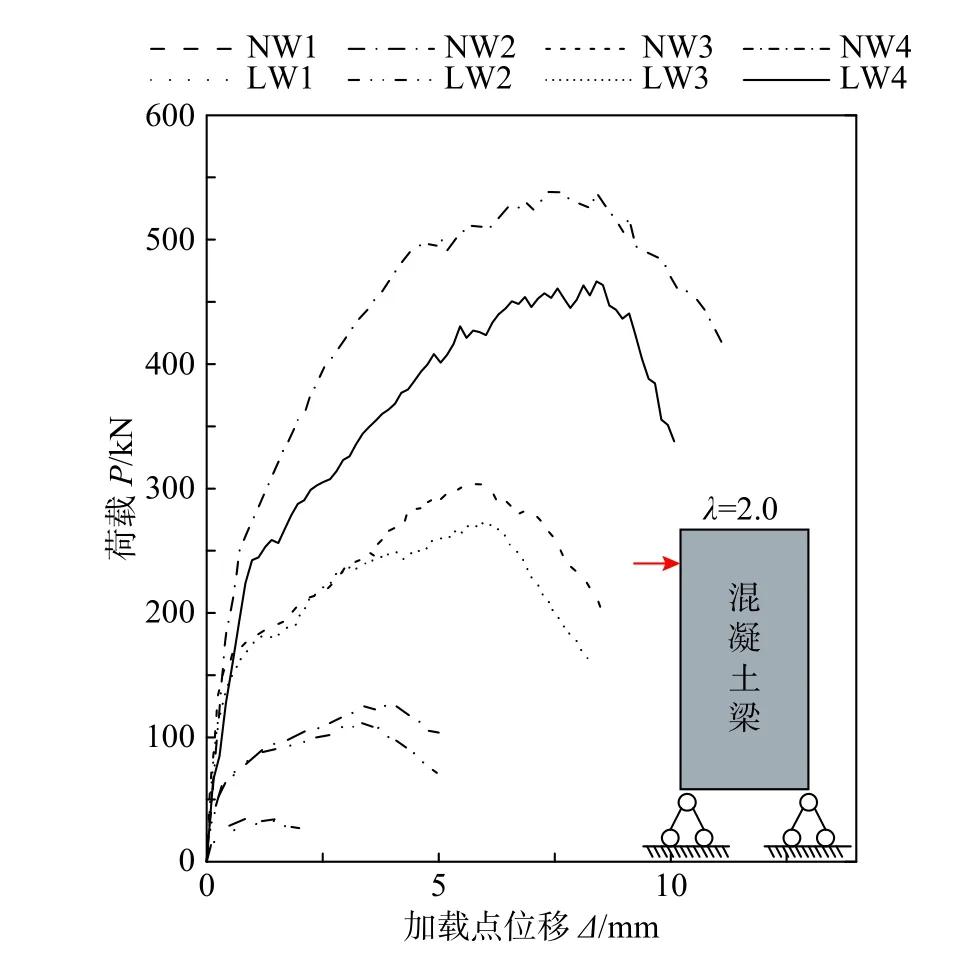
图11 不同尺寸下混凝土悬臂梁试件荷载-位移曲线Fig. 11 P-Δ curves of lightweight aggregate concrete cantilever beam specimens of different sizes
由图11 可知:2 种骨料混凝土悬臂梁在加载初期,曲线都呈线性关系,相同尺寸的两种试件曲线重合率高,这说明这个阶段剪力基本由混凝土承担;加载到极限荷载15%~20%时,曲线的斜率降低,出现明显转折点,悬臂梁刚度开始退化,进入非弹性工作阶段;当快要接近极限荷载时,曲线斜率降低不显著;当达到极限荷载后,曲线迅速下降,试件破坏。此外,随着尺寸增大,轻骨料混凝土梁慢慢达不到普通混凝土梁的最大抗剪承载力,且下降段的曲率越陡,体现了轻骨料试件的脆性,尺寸效应对轻骨料混凝土试件影响更加明显,这与Balendran 等[33]、Ehsan 等[34]的研究结果相符。
3.3 名义剪切强度尺寸效应规律
这里,根据参考文献[35],普通混凝土梁及轻骨料混凝土梁的名义剪切强度σNu定义为:

式中:Pmax为峰值荷载;b 为梁的截面宽度;h0为梁的截面有效高度。
根据上述模拟结果,给出了普通及轻骨料混凝土悬臂梁名义剪切强度σNu与特征尺寸D(这里选取为梁高h)的关系,如图12 所示。
图12 给出了3 组不同骨料分布的2 种不同骨料混凝土梁名义抗剪强度模拟值与尺寸的关系图。可以看出,轻骨料混凝土梁的名义抗剪强度普遍低于普通骨料混凝土梁,但都随构件尺寸的增大而减小,这表明两种骨料的混凝土梁皆有明显的尺寸效应现象。400 mm、600 mm、800 mm梁高普通骨料混凝土梁试件相较于200 mm 梁高试件的名义抗剪强度平均下降3%、6%、9%,轻骨料混凝土梁名义抗剪强度下降百分比为6%、12%、17%,这说明尺寸效应对轻骨料混凝土梁的名义抗剪强度影响更加明显。

从图14 数据点的分布情况可以看出,轻骨料混凝土试件的数据点普遍在普通混凝土试件数据点下方,说明轻骨料混凝土试件脆性大、延性较低。表4 为不同骨料3 组样本所对应的B 和D0数值,可以发现:不同骨料的试件,B 和D0的数值是不同的,且难以给出B 和D0与不同骨料试件之间的定量关系。即Bažant 尺寸效应律不能够反映不同骨料类型对尺寸效应的定量影响。
另外,骨料最大粒径、骨料形状及体积分数等对混凝土的破坏行为及强度等均会产生影响,亦可能会影响混凝土强度的尺寸效应行为。
4 与规范对比及讨论
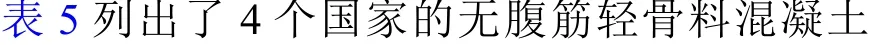
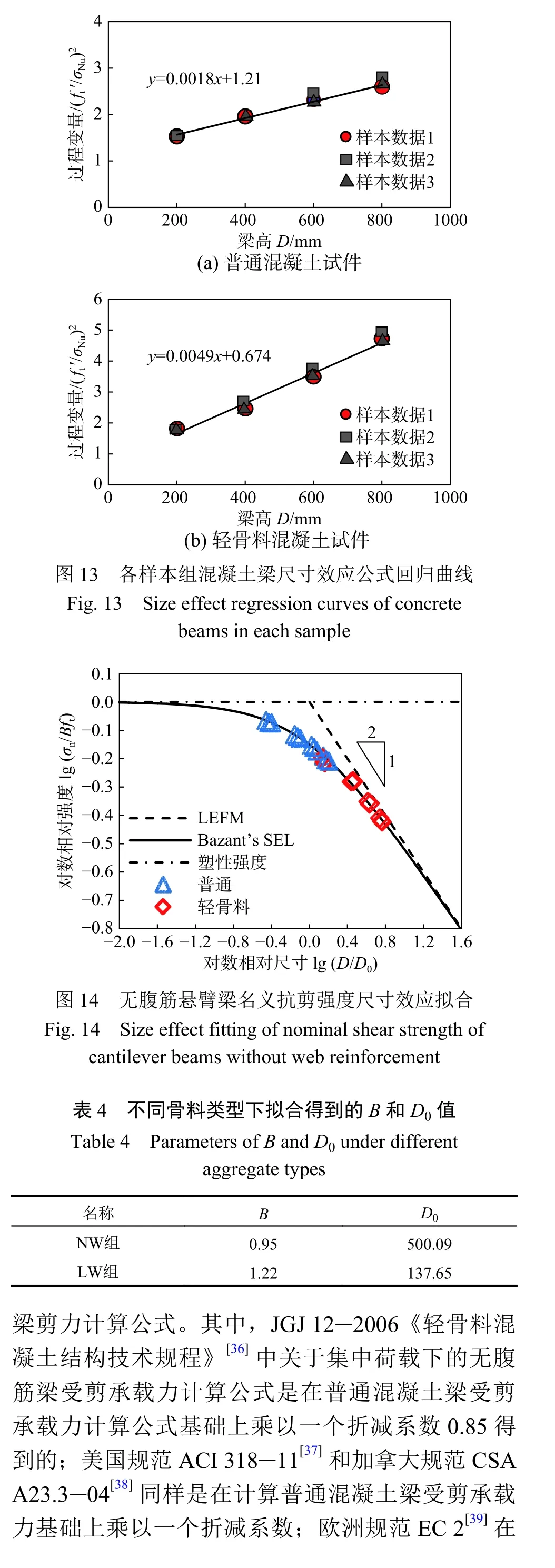
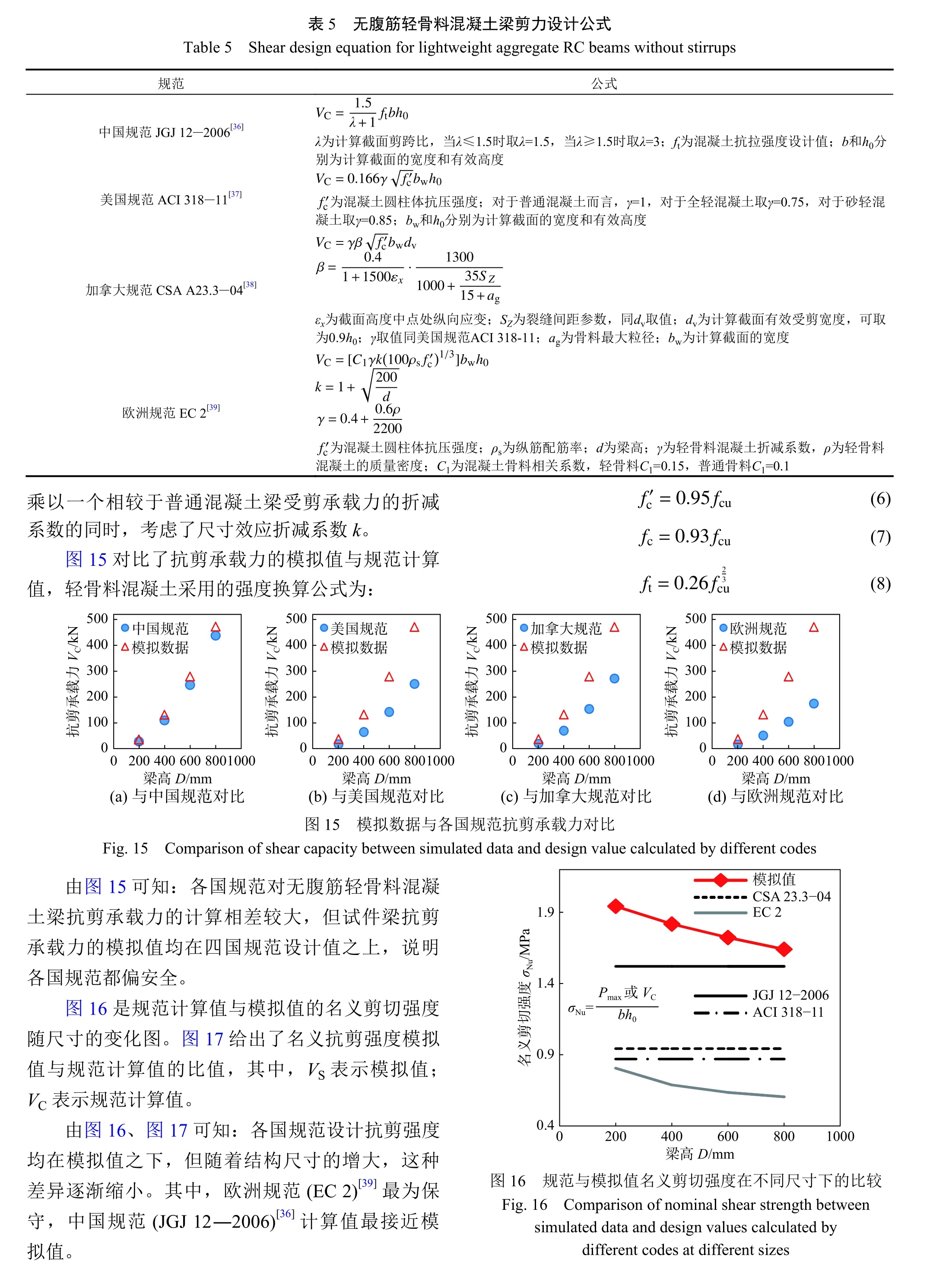
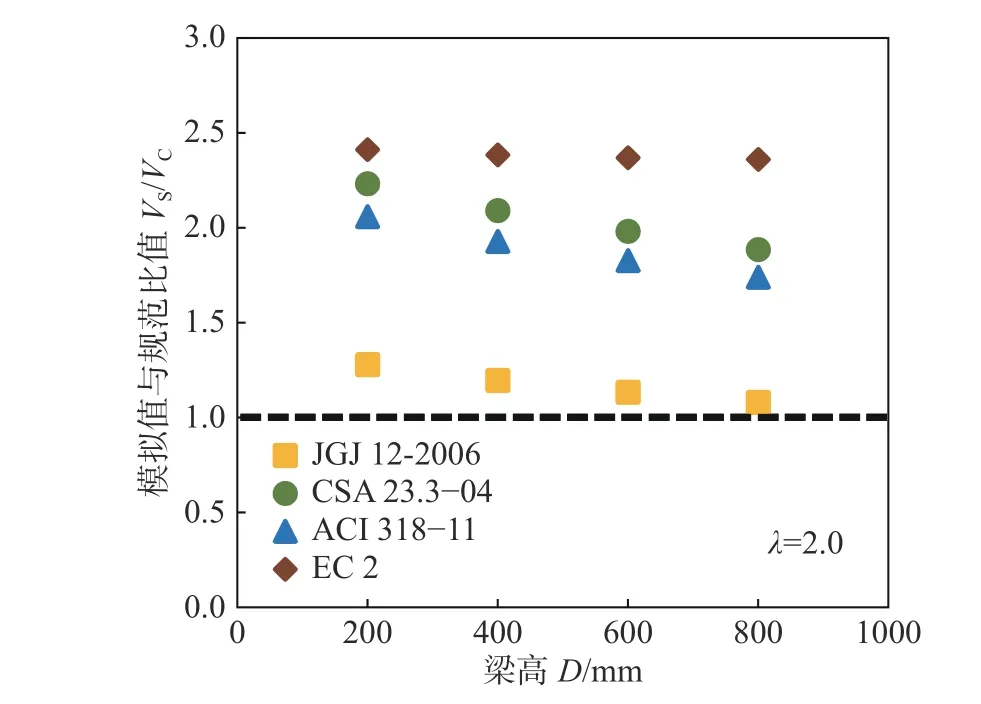
图17 模拟数据与各国规范名义抗剪强度比值Fig. 17 Ratio of nominal shear strength between simulated data and design values calculated by different codes at different sizes
5 结论
本文采用三维细观数值模拟方法,通过对不同尺寸的普通及轻骨料无腹筋混凝土悬臂梁剪切破坏模式与失效机制的研究,结合混凝土材料层次经典Bažant 尺寸效应律分析了其名义剪切强度的尺寸效应规律。此外,结合模拟结果对相关设计规范抗剪承载力计算公式的准确性和安全性进行了初步探讨。得出结论如下:
(1) 区别于普通混凝土梁,轻骨料混凝土梁由于骨料强度较低而首先发生破坏,且更具脆性。
(2) 不同尺寸混凝土梁的剪切破坏模式基本一致,梁的名义剪切强度展现出明显的尺寸效应。
(3) 相同强度等级的轻骨料混凝土梁与普通混凝土梁相比,轻骨料混凝土梁剪切破坏表现出更强的尺寸效应。
(4) 各国规范关于无腹筋轻骨料混凝土梁抗剪承载力的计算中,欧洲规范(EC 2)最为保守,中国规范(JGJ 12-2006)计算值最接近模拟值。
本文仅讨论无腹筋轻骨料混凝土梁剪切破坏的尺寸效应规律。

