梭形空间桁架约束型防屈曲支撑的性能研究

朱博莉，郭彦林

(清华大学土木工程系，北京 100084)

防屈曲支撑(BRB)兼具支撑和耗能双重作用，在高层结构、空间结构、桥梁工程抗震设计及建筑工程抗震加固中有广泛应用[1-3]。防屈曲支撑一般由内核构件和外围约束体系组成[4]。内核构件直接承受轴向荷载作用，其受压时受外围构件的侧向约束而不会发生屈曲，一般采用屈服点低、延性好的钢材。外围约束体系是受弯构件，通过对内核构件提供侧向约束，使其不发生整体失稳，提高了内核构件的承载能力，从而使BRB 的滞回曲线饱满，耗能性能更好。

防屈曲支撑根据外围约束体系的约束能力和构件的耗能性能可以分为承载型和耗能型两种。承载型防屈曲支撑受压不屈曲，改善了构件屈曲引起受压承载力下降的不足，可用于承担单调轴压荷载，要求内核屈服后呈现出一定的延性而不失稳。耗能型防屈曲支撑不仅要求其内核构件达到全截面屈服，而且应该满足位移相关型耗能器的性能要求，如《建筑抗震设计规范》(GB 50011－2016)[5]中要求在设计位移幅值下往复循环30 次后，主要设计指标误差和衰减量不应超过15%；在 AISC 341－05[6]中，通过要求屈曲约束构件的累积塑性应变能力达到一定数值来实现。为此，耗能型BRB 的内核钢材具有足够的塑性变形能力，外围约束构件应具有一定的约束刚度，即BRB 的设计约束比不低于其相应的门槛值。很显然，由于耗能型防屈曲支撑对延性要求更高，其约束比门槛值要大于承载型防屈曲支撑。前人的研究结果表明，对于采用不同外围约束体系的BRB，其约束比的门槛值规定也不尽相同[7]，需要研究其整体失稳破坏机理并建立对应的设计方法。

在防屈曲支撑的设计理论研究中，主要围绕着外围约束结构体系的革新以及提高其约束效率为主线进行研究，以满足工程的不同需求及经济的设计。对BRB 的研究现状，从其外围约束结构体系的革新和发展分类：第一类为钢筋混凝土约束型BRB[8-9]；第二类为钢管混凝土约束型的BRB[10-13]；第三类为全钢约束型BRB[14-17]。BRB的概念于1971 年由日本学者Yoshino 和Karino[18]提出后，就广泛应用于高层结构的抗震设计，而且对BRB 的外围约束型式、受力机理和设计方法的研究较多。BRB 约束比的概念最初是由Kimura等[19]提出，定义为构件弹性屈曲荷载与内核全截面屈服荷载的比值，是BRB 设计的关键参数，其兼具衡量构件外围约束体系的约束刚度及支撑的承载性能。按照限制BRB 的约束比不小于某一特定值(定义为约束比门槛值)进行设计，可保证BRB 整体的稳定性。鉴于约束比门槛值设计方法概念清晰，也便于设计人员掌握，众多国内外学者对不同类型的BRB 的约束比门槛值进行了研究。Kimura 等[19]对钢管混凝土约束型BRB 进行了试验研究，并依据试验结果给出了此类BRB 的约束比门槛值为1.9。Fujimoto 等[20]根据研究成果建议，将钢管混凝土约束型BRB 的约束比取值限定在1.5～2.17 范围内，这一成果已被日本的《钢结构稳定设计建议》采用。Tada[21]基于大量的试验结果，提出了钢管混凝土约束型BRB 累计塑性应变与约束比之间的关系，从而可根据对累计塑性应变的要求来确定约束比门槛值。郭彦林和江磊鑫[22]提出了型钢组合装配式BRB，基于外围约束构件边缘纤维屈服准则，推导了不考虑内核与外围间隙和材料应变硬化影响的约束比门槛值计算公式。郭彦林和王小安[23]对全钢装配式BRB 进行了数值分析和试验研究，主要研究了四槽钢装配组合及四角钢装配组合形成的BRB 失稳机理、单调承载力和滞回性能，并依据其外围约束体系抗弯承载力的极限状态，推导了约束比门槛值计算公式，其中考虑了内核与外围间隙、荷载的初偏心以及内核双向弯曲变形的影响。

近年来，BRB 的外围约束体系特别注重高承载效率的设计。Guo 等[24]提出了内核分离式防屈曲支撑，通过拉大分肢间距使外围约束体系截面更加展开，显著提高了防屈曲支撑的整体抗弯刚度和承载效率。借鉴于轴心受压柱屈曲后截面弯矩沿高度呈梭形变化的分布特点，提出了梭形圆钢管约束型防屈曲支撑[25]，并对其承载性能进行了研究。为了满足超长、高承载力防屈曲支撑的工程需求，近期提出了桁架约束型防屈曲支撑，并对其设计理论进行了研究[26-27]。

综上所述，依据工程需求不同对BRB 外围约束体系进行革新，并对其轴向单调加载承载力和轴向往复荷载下的滞回性能进行研究，提出其最小约束比的设计方法，也是本文研究的主要目的。

1 研究对象及内容

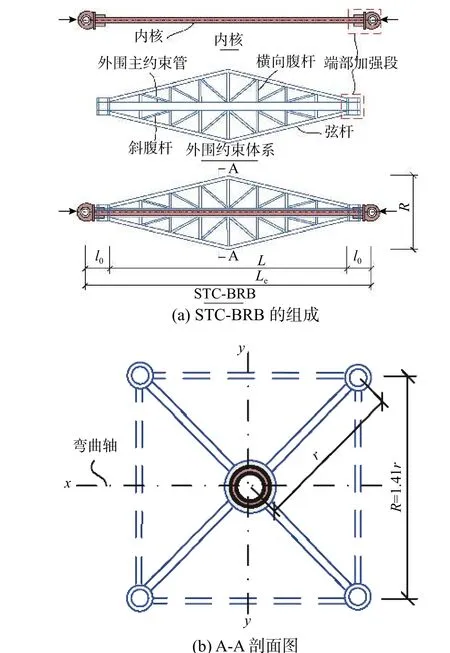
图1 STC-BRB 的组成Fig. 1 Components of STC-BRB

结合前述对BRB 研究的综述，本文提出了一种梭型空间桁架约束型BRB(STC-BRB)，如图1所示。STC-BRB 把梭形受压构件和受弯桁架的受力特点相结合，具有造型美观、承载效率高且设计经济的优点。众所周知，两端铰接的轴向受压构件屈曲时会发生侧向挠曲变形，其截面弯矩沿构件轴向呈中间大、两端小的分布模式，采用与其弯矩分布图相似的纵向梭形构件能改进截面轴向应力的均匀程度，提高材料的利用率，获得更为经济的设计[28-30]。更重要的是，采用梭形桁架作为外围约束体系，扩大了截面的整体高度，BRB发生侧向弯曲时力臂更大，因而，整体抗弯刚度显著提高，而且，外围桁架约束体系把弯矩作用转化成桁架构件的轴力作用，外围约束体系受力更加合理和高效。可以预见，这类防屈曲支撑能跨越大空间、具有高承载力以及构件轻量化等优点。此外，梭形桁架约束体系外形美观，用于高层建筑和空间结构的外露防屈曲支撑构件的设计，能增加视觉美感效果。

STC-BRB 是由梭形桁架外围约束体系与内核钢管组成。外围梭形桁架约束体系采用主约束钢管和多道弦杆、横腹杆、斜腹杆组成的三角桁架，共同与主约束钢管连接，对内核钢管提供侧向约束作用。外围梭形三角桁架约束体系中的弦杆、横腹杆、斜腹杆均选用圆钢管，且直径不大于主约束钢管：横腹杆沿纵向均匀布置，一端焊接在外围主约束钢管上，另一端焊接在外侧弦杆上。布置在外侧的弦杆在BRB 端部收拢并与外围主约束钢管焊接相连。STC-BRB 内核构件采用等截面的无缝圆钢管，通过限制其内核钢管的径厚比来规避其在轴压力作用下的局部屈曲，设计时应采用厚实截面[31]。主约束钢管的内直径要略大于内核钢管的外直径，从而能够在两者之间保留合适的间隙，避免内核构件受压时对外围主约束管产生环箍效应。

BRB 的设计和设计理论包含三个方面：第一是内核构件材料的设计，除了满足截面承载力外，更要关注组成内核构件板件的局部屈曲、材料的屈服强度和其延性性能，如内核构件采用圆钢管，由于其钢管内部不设置任何约束构件，要求内核钢管在达到屈服荷载后也不发生局部屈曲，故其径厚比限值要求更加严格；第二是整体稳定性设计，即在满足相关耗能指标要求的情况下BRB 整体不失稳，这一设计要求可通过满足BRB 最小约束比或约束比门槛值实现；第三是端部节点的构造设计，同理，在完成其耗能要求的条件下端部连接节点不先于BRB 整体失稳而破坏。为了防止端头不发生过早的强度破坏，在STC-BRB 端部采用加强措施，其具体构造设计也在图1 中显示。本文重点研究STC- BRB 的整体失稳机理，进而，确定其约束比的设计门槛值。同时，假定外围约束体系的钢管和相邻节点之间的主约束钢管受压失稳不先于STC-BRB 的整体失稳发生，即要求梭形桁架的弦杆分肢长细比(对应于弦杆两相邻节点的距离)和相邻节点之间的主约束钢管的长细比不应大于STC-BRB 整体长细比的0.5 倍[32]。这一条件在后面有限元数值算例设计中均能满足。

本文研究STC-BRB 受力机理及设计方法：首先，理论上推导STC-BRB 的整体弹性屈曲荷载的表达形式，建立与STC-BRB 斜率变化以及截面刚度常数之间关系；同时，采用梁单元有限元模型进行弹性屈曲分析，确定STC-BRB 整体弹性屈曲荷载的近似计算公式，以便于给出STC-BRB 约束比计算的表达式；最后，分别进行轴压荷载作用下的弹塑性静力承载力以及轴向往复拉压荷载作用下的滞回耗能分析，剖析STC-BRB 的约束比变化对其静力承载能力、延性能力、滞回耗能性能以及破坏机理的影响，研究承载型构件和耗能型构件的约束比门槛值大小，为其STC-BRB 的静力和抗震初步设计提供依据。

2 弹性屈曲性能

如前所述，BRB 的弹性屈曲荷载是定义其设计约束比的重要参数。本节对STC-BRB 弹性屈曲荷载进行参数研究，考察梭形桁架约束体系L/R 及截面主要几何参数对STC-BRB 弹性屈曲性能的影响，试图给出STC-BRB 的整体弹性屈曲荷载的近似计算公式。

2.1 有限元模型

图2 给出了STC-BRB 的组成及工作机理的简化计算模型，它反映了STC-BRB 的外围约束体系与内核构件之间的受力机理及位移协调关系，也可作为STC-BRB 平面内整体弹性屈曲分析的有限元模型，定义为有限元模型1。本研究假定STCBRB 两端铰接，在有限元模型中的计算长度为L 而不是Le(图1)，是因为本文仅涉及STC-BRB的整体稳定性能的研究，不包括端部节点的细部构造和强度设计。因此，STC-BRB 的计算长度L=Nl1，N 为主约束钢管被横腹杆所分割的段数。从图2 可见，外围约束结构体系保持对内核的侧向约束，实现内核构件与主约束钢管之间点-点的侧向挠曲位移(y 方向)耦合，保证二者在相应有限元节点处侧向位移相同。此外，二者轴向位移(z 方向)仅在跨中耦合，以消除二者之间的z 向错动，而在其他有限元节点处，轴向位移维持相互独立。约束内核构件两端的侧向位移(x 和y 方向)及内核与约束主管绕自身轴(z 轴)的扭转角；约束内核一端的轴向位移，放开另一端的轴向位移且施加轴向荷载P。内核构件、主约束钢管、弦杆以及连接弦杆与主约束管的腹杆均采用BEAM188，弹性模量取E=206 GPa，泊松比ν=0.3。

图2 STC-BRB 简化分析模型和有限元模型Fig. 2 Simplified analytical model and finite element model of the STC-BRB

2.2 弹性屈曲荷载

采用有限元软件ANSYS[33]对STC-BRB 进行弹性屈曲分析，重点研究构件关键几何参数与其弹性屈曲荷载的相关关系。首先，设计STC-BRB数值分析算例(见表1)，然后，采用有限元模型1 对2 组共171 个STC-BRB 算例的整体弹性屈曲荷载进行计算，研究STC-BRB 的整体弹性屈曲荷载与内核构件屈服荷载比值(Pcr/Py,c)和STC-BRB长度与跨中横腹杆长度比值(L/R)的相关关系，其中L/R∈[5, 50]，参数范围覆盖较宽，包含了工程常用范围。由于外围约束桁架的弦杆斜率较小，弦杆的长度近似取为l1，同时为方便加工，斜腹杆与横腹杆杆件选用相同截面。STC-BRB 的几何尺寸如图1 所示。

表1 STC-BRB 算例的几何尺寸Table 1 Geometric sizes of numerical examples of STC-BRB

可见，表1 中最后一列是应用有限元模型1计算获得STC-BRB 的整体弹性屈曲荷载Pcr与内核初始屈服荷载Py,c之比，图3 给出了其弹性屈曲模态。计算结果表明，STC-BRB 的整体弹性屈曲荷载Pcr与内核初始屈服荷载Py,c之比在0.41～9.79 范围变化，其典型的整体弹性屈曲模态为对称单波屈曲模态。可以预测，STC-BRB 弹性屈曲模态与带斜腹杆的梭形钢管格构柱的弹性屈曲模态相同[34]，尽管二者的受力机理和组成有显著区别。

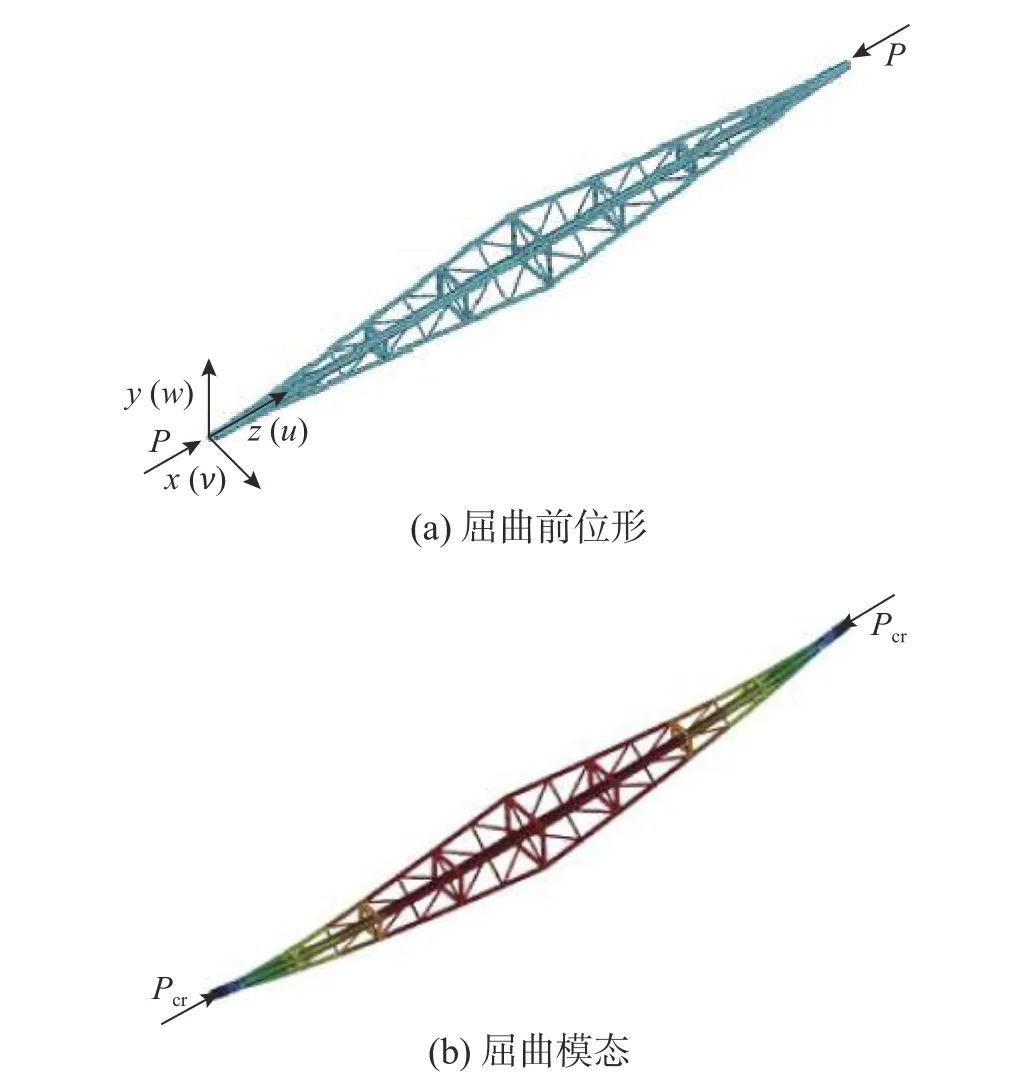
图3 STC-BRB 的弹性屈曲模态Fig. 3 Elastic buckling mode of the STC-BRB

图4 给出了STC-BRB 整体弹性屈曲荷载与分隔数N 和长度L 以及L/R 对其整体弹性屈曲荷载的影响。图4 中给出了STC-BRB 的2 组算例弹性屈曲荷载与内核构件屈服荷载比值(Pcr/Py,c)与柱长与跨中宽度比值(L/R)的相关关系曲线，可见STC-BRB 的弹性屈曲荷载与L/R 密切相关。从图4中的计算结果也可发现，由于在外围约束桁架中布置了斜腹杆，增强了外围约束体系的抗剪刚度，与仅设置横向腹杆的梭形格构柱比较，STCBRB 第一阶整体弹性屈曲模态始终呈现为对称的单波对称屈曲模态。

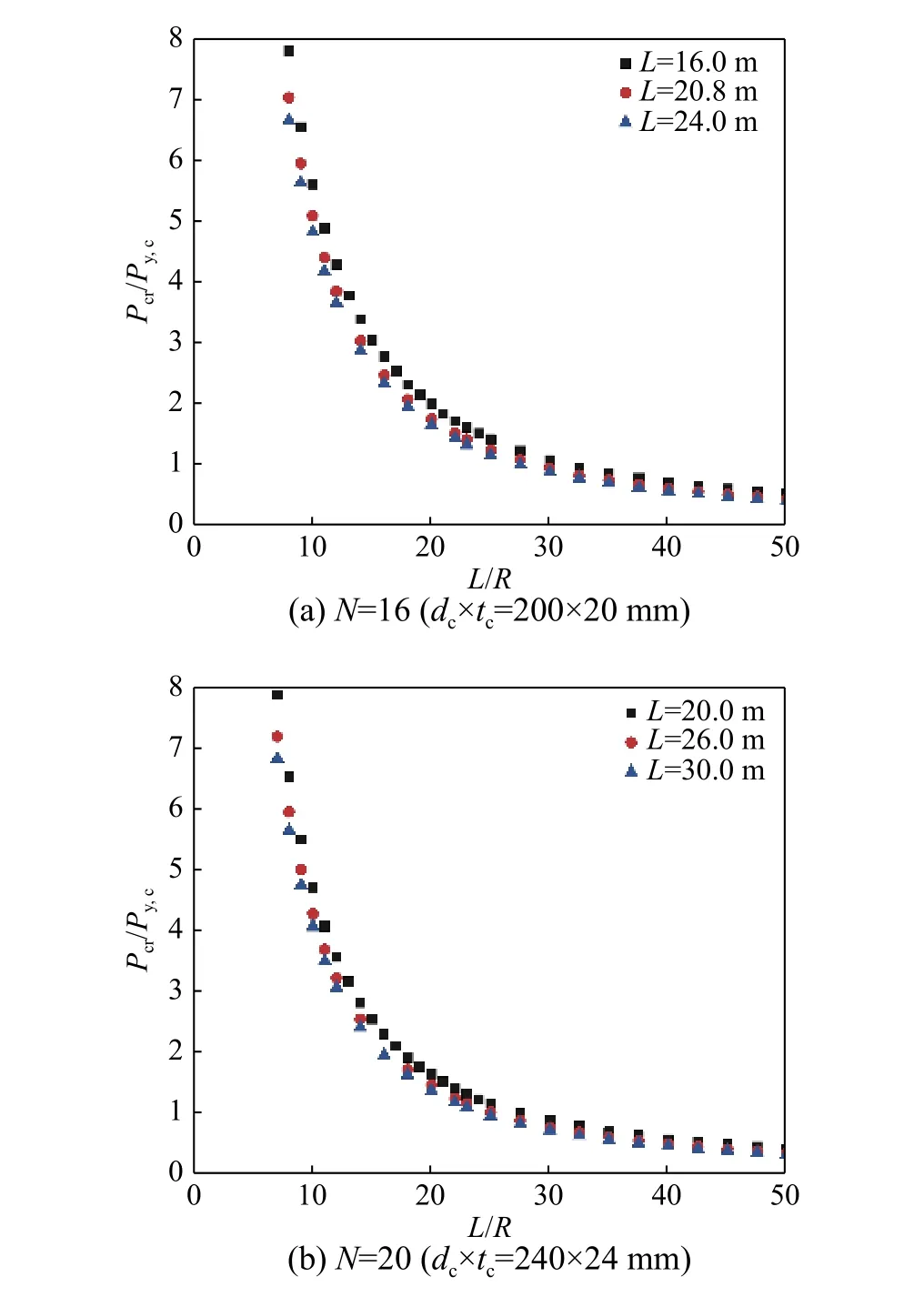
图4 STC-BRB 弹性屈曲荷载与L/R 比值之间的关系Fig. 4 Relationship of elastic buckling loads and L/R in STC-BRB

STC-BRB 两端铰接且内核受轴压作用。STCBRB 中内核构件和外围主约束管均为圆管截面，其弹性屈曲荷载可用欧拉荷载代替。借鉴等截面空间桁架约束型BRB 的整体弹性屈曲荷载[26]，采用平衡法可以给出STC-BRB 在轴压作用下考虑截面剪切变形(仅考虑外围约束桁架的剪切刚度)的弹性屈曲荷载 Pcr表达式，如式(1)所示：

式中：Pcr,c=π2EIc/L2和Pcr,tu=π2EItu/L2分别为内核构件、外围主约束管对应的弹性屈曲荷载；Pcr,tru为外围约束体系中梭形桁架不考虑剪切变形的弹性屈曲荷载；Ktru为梭形桁架跨中截面的剪切刚度。式(1)中，因为外围约束桁架沿轴线呈梭形形状，故采用跨中截面的抗弯刚度和剪切刚度会引入误差。此外，STC-BRB 整体屈曲时，内核钢管构件、外围主约束钢管和桁架外围约束之间会存在相互作用，式(1)右边对应弹性屈曲荷载的简单叠加也会引入误差。因此，式(1)中右边第三项需要修正，故引入修正系数 λm。

图5 给出了表1 中算例的弹性屈曲荷载的有限元解和式(1)的计算结果。图中Py,c为内核全截面屈服荷载。从图5 比较可见，式(1)和有限元计算结果最大误差为5%，与有限元吻合很好。有限元计算结果与式(1)计算结果之间的最大误差不超过5%，故采用式(1)用于计算STC-BRB 的整体弹性屈曲荷载。

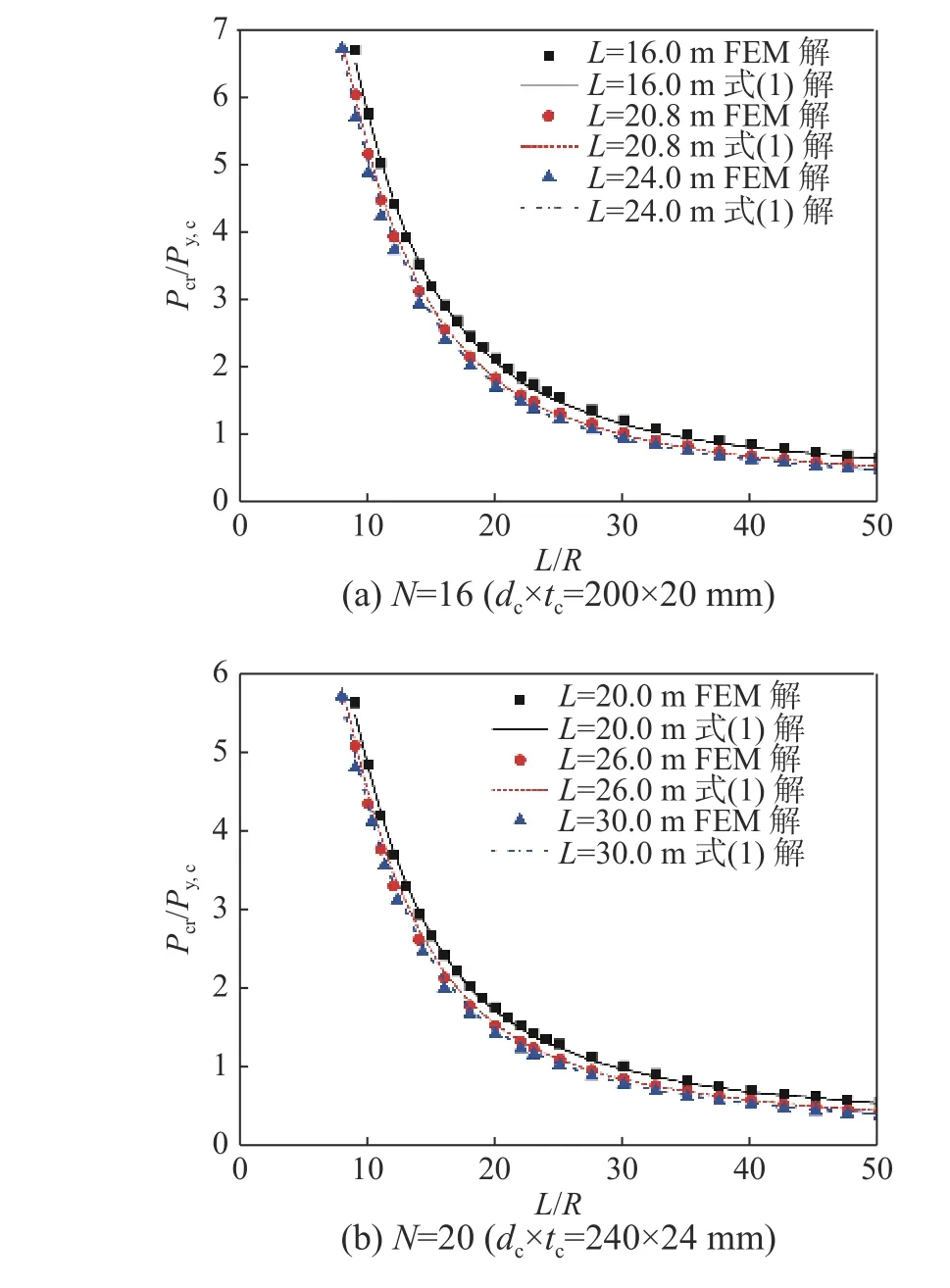
图5 STC-BRB 弹性屈曲荷载的数值解和理论解Fig. 5 Numerical verification and modification of elastic buckling loads of STC-BRB

3 弹塑性静力承载力

STC-BRB 的弹塑性极限承载力有限元数值分析要考虑STC-BRB 整体初始几何缺陷的影响。由于STC-BRB 制作所导致的初始几何缺陷分布的随机性，本文通过有限元法研究了单波对称初始缺陷模式、双波反对称初始缺陷模式以及两者的组合模型[35-37]对STC-BRB 承载性能和耗能性能的影响。计算结果表明，STC-BRB 的最不利初始缺陷模式为其第一阶屈曲模态，即单波对称初始缺陷模式。本文中弹塑性承载力分析中，STC-BRB的初始缺陷采用单波对称初始缺陷模式，其缺陷幅值取为L/500。

3.1 有限元模型

STC-BRB 的弹塑性静力极限承载力分析仍采用有限元软件ANSYS，所有构件采用梁单元BEAM188 模拟，有限元模型定义为有限元模型2，其内核构件与外围约束主管位移耦合情况同有限元模型1。内核构件采用双线性等向强化模型(BISO)，材料采用Q235 钢材，屈服强度fy=235 MPa，其初始屈服后应变硬化模量取2%E，材料塑性扩展服从von Mises 屈服准则。外围主约束钢管及梭形三角桁架弦杆、腹杆材料采用Q345，材料假定为理想弹塑性。弹性模量E=206 GPa，泊松比ν =0.3。

在弹塑性分析中，STC-BRB 算例的约束比ζ取1.0～3.0，算例能够覆盖工程中常用约束比门槛值的取值范围。分析图6 中STC-BRB 的弹性屈曲计算结果可以看出，当算例的约束比 ζ为1.0～3.0时，其L/R 大概为8～15，此时，外围约束体系跨中宽度R 与弦杆节间距 l1(l1=L/N)的比值为0.8～2.5，STC-BRB 外形美观合理，且在工程设计常用范围内。因此，在本节单调轴向加载的弹塑性承载力分析以及后续滞回性能分析中，算例设计时STC-BRB 长度与跨中宽度比值L/R 取8～15，由此，反算外围约束体系梭形桁架的跨中腹杆高度r，其中r 取0.05 m 的整倍数。

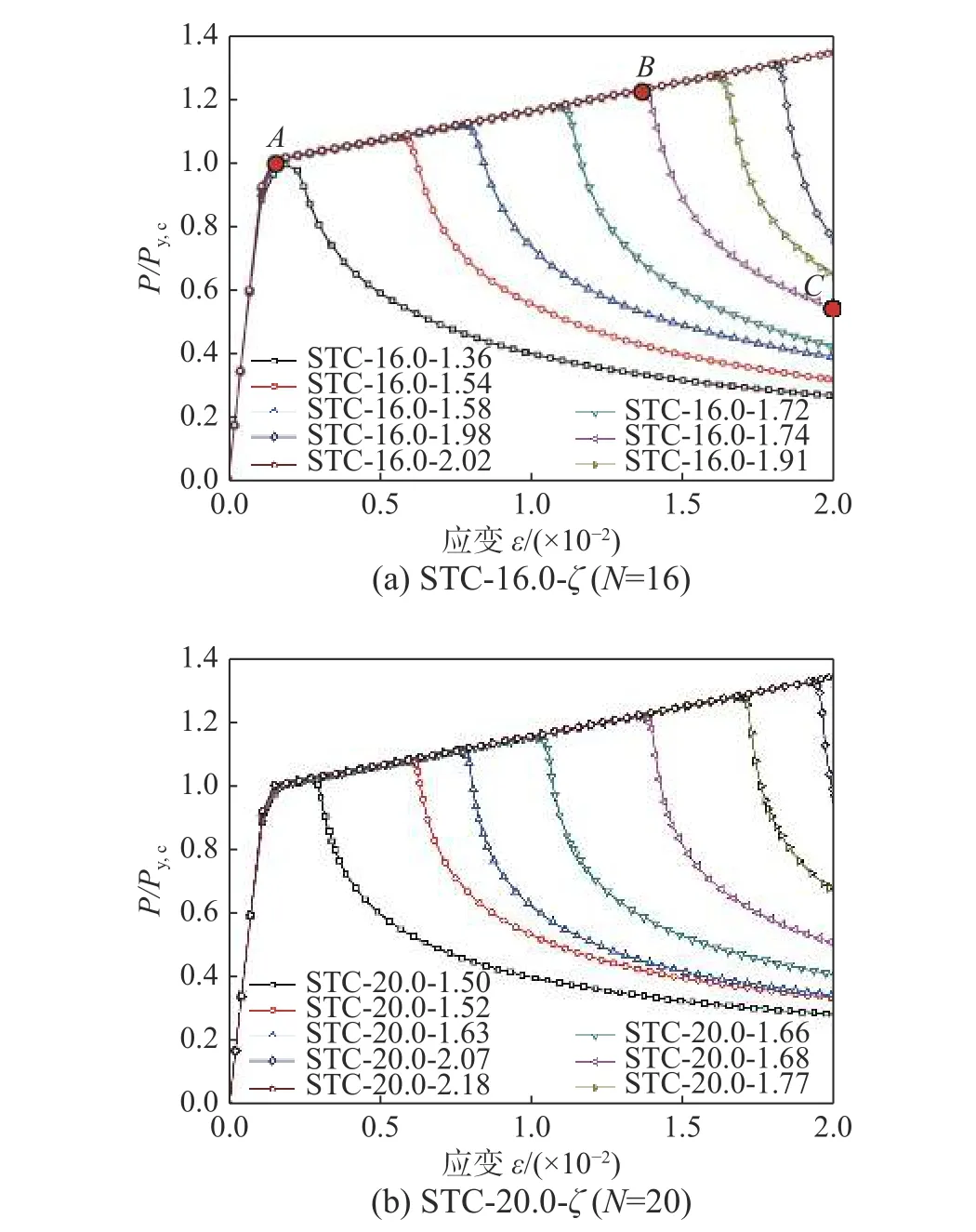
图6 STC-BRB 的荷载-位移曲线Fig. 6 Load-displacement curves of STC-BRB

基于算例的上述选择条件，根据内核构件尺寸和外围约束桁架的分隔数N 设置了两组算例，如表2 所示。其中，表中约束比 ζ按照式(5)计算。为保证外围约束主管壁厚为整数，算例中主约束管直径均取为偶数；外围约束桁架跨中宽度r取0.05 m 的整倍数，均间隔0.05 m。

3.2 极限承载力

采用有限元模型2 对表2 算例进行弹塑性承载力分析，在构件右侧内核上施加轴压位移进行单调加载(图2)，直到内核构件的轴向压缩应变达到εmax=0.02[5]为止，计算可获得STC-BRB 在轴向单调荷载作用下的轴压荷载与轴向位移或轴向应变曲线以及抗压极限承载力。给STC-BRB 施加对应于一阶屈曲模态的几何初始缺陷，其初始缺陷幅值取为构件长度的1/500，其中，等效考虑了STC-BRB 残余应力的附加影响。图6 和图7 给出了部分算例的荷载-位移曲线以及构件在不同加载状态下的变形及应力分布图。算例编号为STC-Lζ，其中，STC 代表梭形桁架约束型BRB；L 为STC-BRB 长度(见图2)；ζ 为STC-BRB 约束比。

对表2 中2 组算例进行轴压承载力分析，获得的轴向荷载-轴向应变曲线绘制在图6 中，分别对应于表2 中N=16，L=16.0 m 和N=20，L=20.0 m两组算例。以L =16.0 m的一组算例说明STC-BRB约束比变化对STC-BRB 受力性能的影响。借助柱子稳定系数的定义，可定义STC-BRB 的极限荷载与内核屈服荷载之比为φ=Pu/Py,c，其中：Pu为STCBRB 单调加载极限承载力；Py,c为STC-BRB 内核的初始屈服荷载。对于约束比ζ ＜1.0的STC-BRB而言，其外围约束刚度小，在其内核屈服前必然发生整体失稳，其φ 也必然小于1.0。

对于图6(a)中1 .0≤ζ ＜2.0的7 个算例，其约束比随着外围约束桁架刚度的增加而增大。当内核轴向压应变 ε=0.001时内核全截面屈服，其φ≥1.0。之后内核进入强化阶段，随着轴向压应变的增加其 φ缓慢上升。当轴向压应变还未达到2%时，支撑发生整体失稳，其轴向承载力迅速下降。根据有限元模拟过程可知，主要由STC-BRB的外围约束体系在偏端部区域塑性区扩展而引起整体失稳。图7 给出了算例STC-16.0-1.74 在内核刚达到屈服、极限状态和最终状态时的内核构件及外围约束桁架的von Mises 应力分布和侧向变形分布图。

表2 STC-BRB 静力承载力分析的算例尺寸Table 2 Geometric sizes of numerical examples of STC-BRB under axial monotonic load

图7 STC-16.0-1.74 的应力分布和变形图Fig. 7 Stress distributions and deformations of STC-16.0-1.74

对于图6(a)中算例STC-16.0-2.02 而言，其约束比ζ 较大，因此，在内核应变达到2%时支撑都没有发生整体失稳。从支撑内核初始屈服到应变达到2%，内核材料的强化效应明显，支撑内核对应于应变2%时的 φ=1.37。观察有限元计算结果可知，支撑的外围约束体系在加载过程中均保持弹性，因此，支撑没有出现整体失稳破坏。

图7 给出算例STC-16.0-1.74(图6(a))在不同加载阶段(A 点、B 点、C 点)的von Mises 应力分布和侧向变形图。当STC-16.0-1.74 的轴向外荷载达到内核构件的屈服荷载时，内核构件全截面达到屈服；此时，外围约束体系处于弹性阶段，最大von Mises 应力为1 89 N/mm2，其中，外围约束主管应力较小，如图7(a)所示。随着轴向力的增加，STC-BRB 的内核全截面屈服并进入强化阶段，当其达到极限状态时，外围约束体系的桁架弦杆率先屈服，屈服区域分布于腹杆与弦杆的节点区域，此时，外围约束主管仍处于弹性状态，如图7(b)所示。达到极限状态后继续对STC-16.0-1.74 进行加载直至 ε=2%时，外围约束体系在1/4 跨(或3/4 跨)靠近端部附近的弦杆发生较大变形，外围约束主管在1/4跨(或3/4 跨)靠近端部附近均已屈服，STC-16.0-1.74 出现与初始缺陷变形模式相似的单波对称破坏模式，如图7(c)所示。

基于表2 中算例的有限元弹塑性分析，STCBRB 在单调加载下的破坏模式及功能要求根据约束比大小可以分为三类：当支撑约束比小，外围约束体系不足以约束内核构件达到全截面屈服即发生塑性变形以致STC-BRB 整体失稳破坏，此为第一类破坏类型；随着外围约束桁架高度的增大，截面的抗弯刚度随之增大，即STC-BRB 的约束比也增大，此时内核构件能达到全截面屈服但仍不能达到2%应变的加载要求，由于内核强化导致内核轴向压力增大，外围约束体系发生塑性变形，支撑发生整体失稳，这是第二类破坏类型；最后一类情况则是STC-BRB 的约束比足够大，能满足内核达到全截面屈服且支撑的轴向压应变达到 ε=2%的要求，支撑还没有发生整体失稳。

在STC-BRB 初步设计阶段，需要对其约束比门槛值有一个保守估计。因此，在图8 中绘制了表2 中算例的约束比 ζ 与 φ之间的关系，可以获得其约束比门槛值的下限。由图8 可知，当STC-BRB的约束比大于2.1 时，此时内核构件的轴向压应变ε≥2%，恰好STC-BRB 不再发生整体失稳，STC-BRB 对应的单调加载极限承载力等于内核初始屈服荷载的1.35 倍。因此，建议STC-BRB 满足0.02ly塑性变形能力的约束比门槛值 [ζ]η=2.1。可以认为，当STC-BRB 的约束比ζ≥2.1 时，其满足内核全截面屈服且具有一定的塑性变形和强化能力的要求。

图8 STC-BRB 的φ -ζ相关曲线Fig. 8 φ -ζ curve of the STC-BRB

4 滞回性能研究

4.1 有限元模型及其有效性验证

同理，本文采用ANSYS 有限元软件对STCBRB 进行轴向往复加载过程的滞回性能分析，对应的有限元模型定义为有限元模型3。在有限元模型3 中内核构件以及外围约束体系均采用BEAM188梁单元，内核构件与外围约束主管位移耦合情况如图2 所示，同有限元模型1。有限元模型3 内核构件采用Q235 钢材，屈服强度fy=235 MPa；外围主约束钢管及梭形桁架弦杆、腹杆材料均采用Q345，fy=345 MPa，且不考虑初始屈服后强化作用。钢材弹性模量E=206 GPa，泊松比ν=0.3。

不同于单调加载，内核构件在轴向往复荷载作用下，往复加载会导致材料强化大幅增加，所以，理想弹塑性本构关系不再适用于滞回加载数值模拟。在对STC-BRB 反复加载滞回性能有限元分析中，ANSYS 软件中材料的双线性等向强化模型BISO 采用了von Mises 屈服准则；材料非线性随动强化模型CHAB 考虑了强化与塑性间的非线性影响，适用于大应变和循环加载。因此，在STCBRB 滞回性能的有限元模拟中，采用了ANSYS提供的非线性随动强化CHAB 模型和双线性等向强化BISO 模型的组合，该组合能很好地模拟钢材的滞回性能，其中，钢材材料BISO 模型不设置强化段。非线性随动强化模型CHAB 叠加了4 种随动强化模型，模型中的参数C 和γ 选取文献[38]中提供的数据：C1=6.0 GPa，γ1=173；C2=6.0 GPa，γ2=120；C3=3.0 GPa，γ3=32；C4=9.9 GPa，γ4=35。

在STC-BRB 弹塑性滞回性能分析中，有限元模型3 所采用的梁单元类型、内核构件与外围约束主管位移耦合情况及材料本构模型与文献[23]完全相同，且文献[23]进行了TTC-BRB 轴向往复荷载作用下的滞回试验研究，已经验证了有限元模型的可靠性。因此，确信有限元数值分析模型(有限元模型3)是可靠的。

4.2 滞回性能

根据《建筑抗震设计规范》(GB 50011－2016)[5]规定，在大震作用下，框架结构的层间位移角不应大于1/50。当BRB 斜向布置时，对应的内核轴向应变约为2%。所以，在STC-BRB 弹塑性滞回分析时，内核构件最大轴向位移取为2%ly。根据美国AISC 341－05[6]建议，位移加载幅值由小到大取为0.25%ly、0.50%ly、0.75%ly、1.00%ly、1.50%ly和2.00%ly这6 个等级，且在每级位移加载幅值水平下进行3 次拉压循环加载。STC-BRB 在反复荷载作用下的加载制度如表3 所示。这里，ly为内核屈服区长度，取值与L 相同。

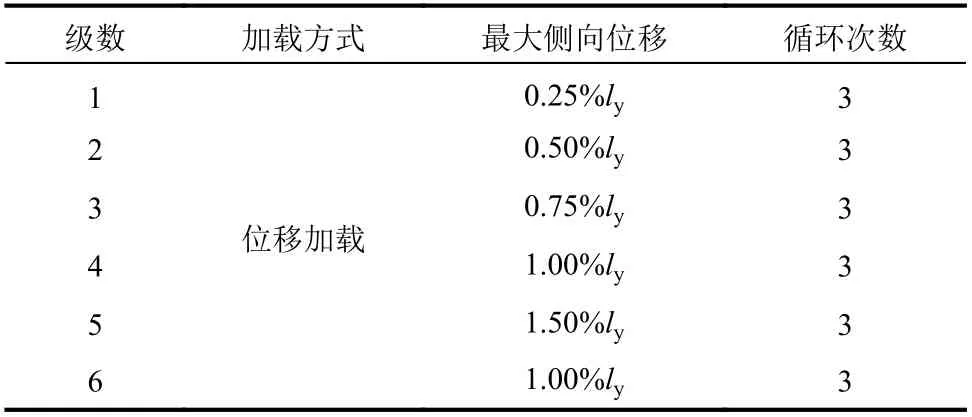
表3 STC-BRB 加载制度Table 3 The loading protocol of STC-BRB

图9 给出了表2 第一组STC-BRB 算例中部分试件在轴向往复荷载作用下的滞回曲线。图9 横坐标为内核构件的轴向压缩应变 ε；纵坐标为STC- BRB 的无量纲轴向荷载比值P/Py,c。算例编号为STC-L-ζ ，其中，STC 代表梭形桁架约束型的BRB，L 为STC-BRB 长 度， ζ为STC-BRB 约束比。

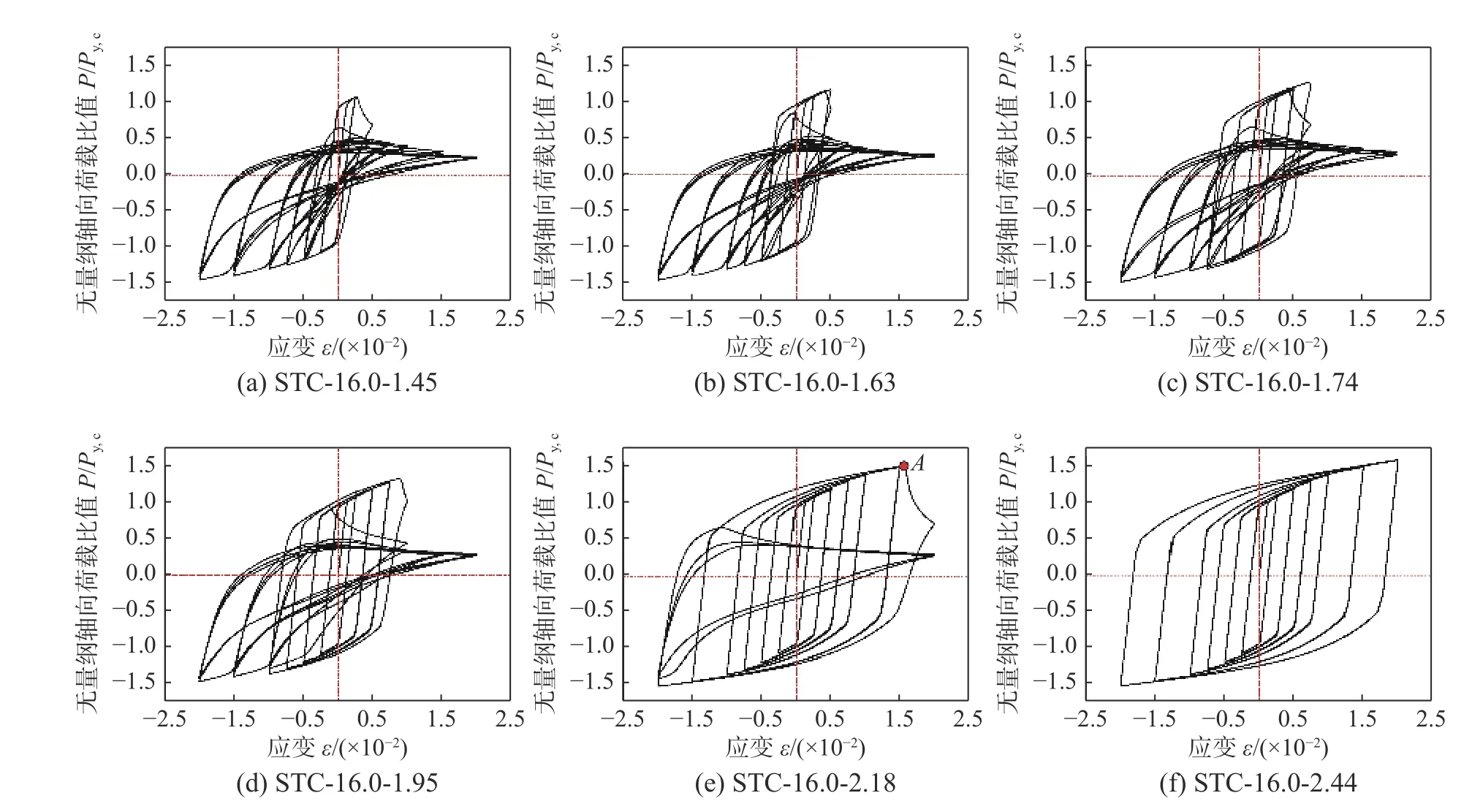
图9 STC-BRB 的滞回曲线 (N=16，L=16.0 m)Fig. 9 Hysteretic curves of STC-BRB (N=16，L=16.0 m)

STC-BRB 的弹塑性滞回分析结果表明，当其滞回分析的(P/Py,c)max在1.35≤(P/Py,c)max＜1.58 范围时，与其对应的STC-BRB 在静力加载过程中，其内核构件虽能达到全截面屈服，但其轴向压应变未达到2%。计算结果显示，这一范围的STCBRB 只能完成低阶滞回加载，其虽然具有一定的耗能能力，但不能满足塑性累计应变值的要求，用于承载型构件尚没有问题，可用于调整复杂结构的抗侧刚度，不能用于结构的耗能设计。当STC-BRB 的(P/Py,c)max=1.58 时，此时，能完成既定的滞回加载过程，滞回曲线完整且饱满，同时，满足AISC 341-05[6]规定的累积塑性变形能力 μc≥200的要求。对应地，STC-BRB 可以作为耗能构件用于结构的抗震耗能设计。图10 给出了STC-16.0-2.18 在轴向往复荷载作用下，极限状态下内核和外围约束体系的应力分布和变形分布图。在极限状态时，STC-16.0-2.18 发生与初始缺陷分布相似的单波对称破坏模式，外围约束桁架弦杆率先屈服，随后外围约束主管屈服，构件破坏。

图10 STC-16.0-2.18 的应力分布和变形图(图9(e)A 点)Fig. 10 Stress distributions and deformations of STC-16.0-2.18 at point A in Fig.9(e)

图11 给出了表2 中全部两组STC-BRB 算例的约束比ζ 与无量纲轴向荷载最大值(P/Py,c)max之间的关系曲线，从图11 可以保守地获得其约束比门槛值的下限。从图11 可见，对于STC-BRB，当其约束比ζ≥2.5 时，支撑可以满足耗能型构件对滞回性能的要求而未发生破坏，滞回曲线完整且饱满，满足AISC 341-05[6]中累积塑性变形能力系数(μc≥200)的要求。鉴于此，STC-BRB 作为耗能型构件的约束比门槛值取为[ζ]ω=2.5。对比文献[27]的计算结果，等截面桁架约束型防屈曲支撑耗能型构件的约束比门槛值大约取值[ζ]ω=3.0。对比说明，STC-BRB 材料利用率提高，其设计经济性更好。

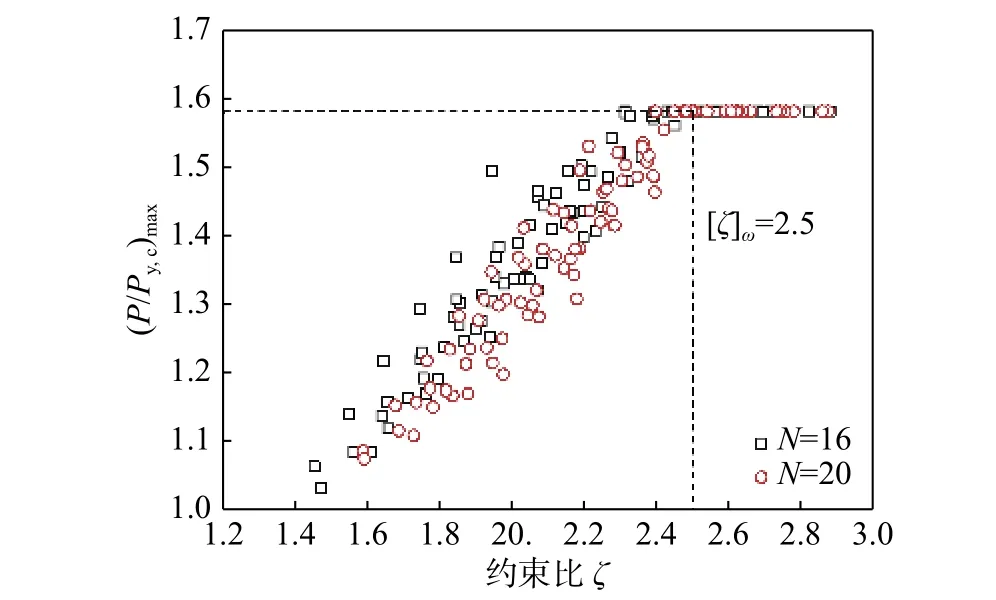
图11 STC-BRB 的(P/Py,c)max-ζ 相关曲线(滞回加载)Fig. 11 (P/Py,c)max-ζ curve of the STC -BRB

综合上述计算结果，耗能型STC-BRB 约束比门槛值[ζ]ω=2.5 大于其承载型STC-BRB 对应的约束比门槛值[ζ]η=2.1。由此可见，耗能型构件对其外围约束体系的抗弯刚度要求更高。对于承载型和耗能型两种BRB，依据工程设计需要区分使用，既保证了构件的使用功能，又节省制作成本。

5 结论

本文提出了STC-BRB 并研究了其弹性屈曲荷载、弹塑性静力承载力以及弹塑性滞回耗能性能。其要点总结如下：

(1) 建立了STC-BRB 整体弹性屈曲荷载的计算公式。采用梁单元模型，研究了STC-BRB 斜率变化及关键几何参数对其整体弹性屈曲性能的影响。计算结果表明，STC-BRB 整体屈曲模态呈现单波对称变形模式，采用式(1)计算STC-BRB 整体弹性屈曲荷载具有较高的精度。STC-BRB 整体弹性屈曲荷载的闭合解为定义其约束比提供了依据。

(2) 研究了STC-BRB 弹塑性静力极限承载性能。变化算例STC-BRB 的约束比，采用梁单元对STC-BRB 在单调轴压荷载作用下的弹塑性承载力进行分析，获得了内核轴向应变达到2%及以上的约束比要求，建议承载型STC-BRB 的约束比门槛值取为[ζ]η=2.1。计算结果也表明，STC-BRB整体失稳破坏主要由偏端部区域的弦杆屈服扩展所致。

(3) 研究了STC-BRB 在轴向往复荷载作用下的滞回耗能性能。根据STC-BRB 在轴向往复荷载作用下的滞回耗能数值计算结果，获得了满足AISC 341-05[6]中累积塑性变形能力系数(μc≥200)要求的约束比门槛值，建议耗能型STC-BRB 的约束比门槛值取为[ζ]ω=2.5。