基于带通采样的抗混叠滤波器设计
樊佳恒,王洪梅,王法广,李世银,李宗艳,刘玉英
(中国矿业大学 信息与控制工程学院,江苏 徐州 221000)
0 引 言
作为实现无线通信的重要方法和手段,软件定义无线电(software defined radio,SDR)在无线通信中被广泛应用。为将软件无线电尽可能多的功能通过软件算法实现,需对其工作频带内的射频信号(如0.8 GHz-3 GHz)进行采样,而带通采样定理的应用可以用较低的采样速率正确反映带通信号的特性[1,2],并且为后面的实时处理奠定基础。
然而,在采样过程中,有用信号混叠问题的普遍存在影响了多模式、多频段信号在同一平台上的正常接收[3,4],因此,如何有效地消除混叠成为基于软件无线电信号接收的一个研究热题。传统的,大部分学者通过更改采样频率的方式来避免混叠发生[5-7]。很多学者也致力于寻找新的算法来简化频率选择过程[8-10],但是这些方法为避免产生混叠必然会限制采样频率的选择,同时繁琐的计算过程也增加了实现的难度。
目前一些新的研究集中在改进采样结构[11-13],并提出了多通道采样,广义正交带通采样(GQBPS)和优化的均匀带通采样(OUBPS)等[14],例如,重建带限信号形成与线性规范变换(LCT)相关联的多通道样本[15],但是这些采样方法需要复杂的重构算法。为解决上述技术问题,本文基于二阶带通采样提出了一种软件无线电多带通信号接收方法,实现了软件无线电对多带通信号的无混叠接收,并且大大简化了模拟前端。
1 二阶带通采样
假设待采样的射频带通信号为R(f), 其带宽为B。 采用采样频率fs为fs=2B。 所有在以下频率区域内的信号都定义为索引为n的信号,我们定义n为位置索引
(n-1/2)fs<|f|<(n+1/2)fs
(1)
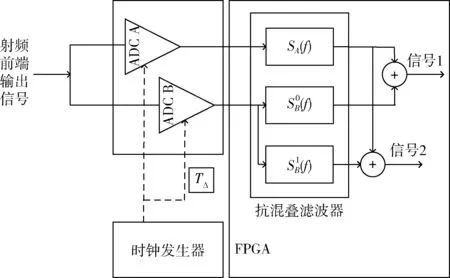
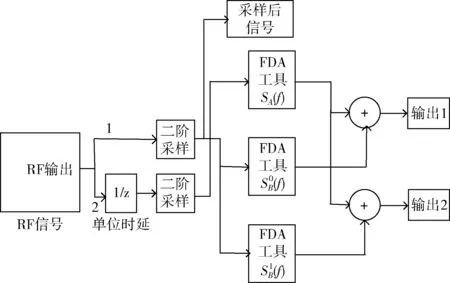
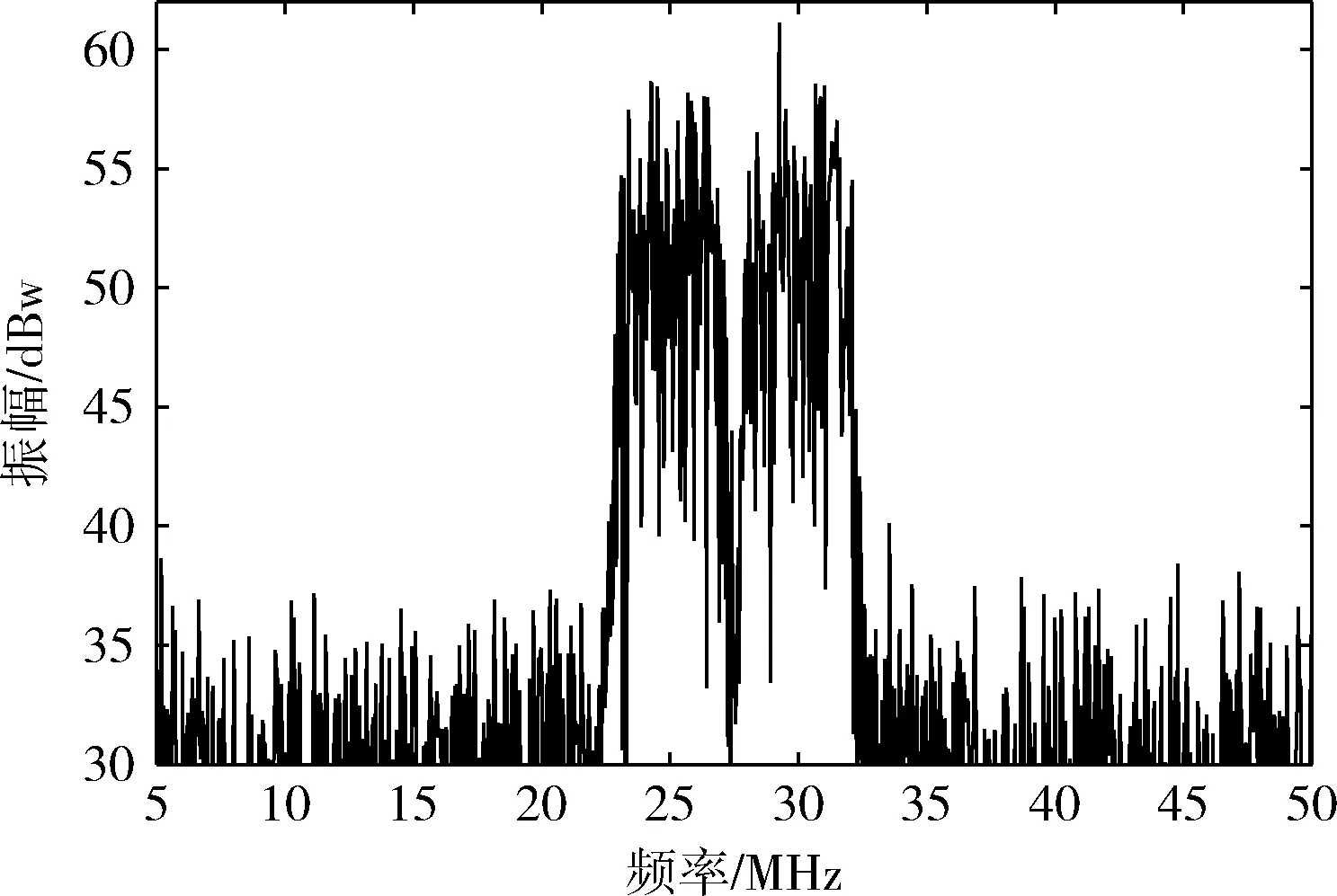
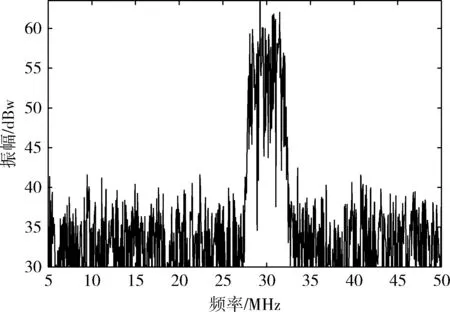
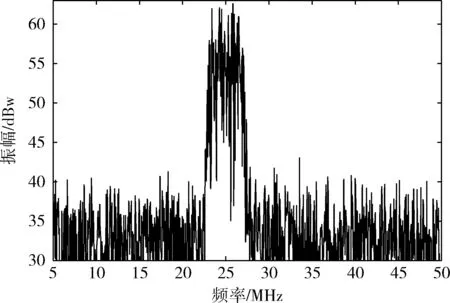
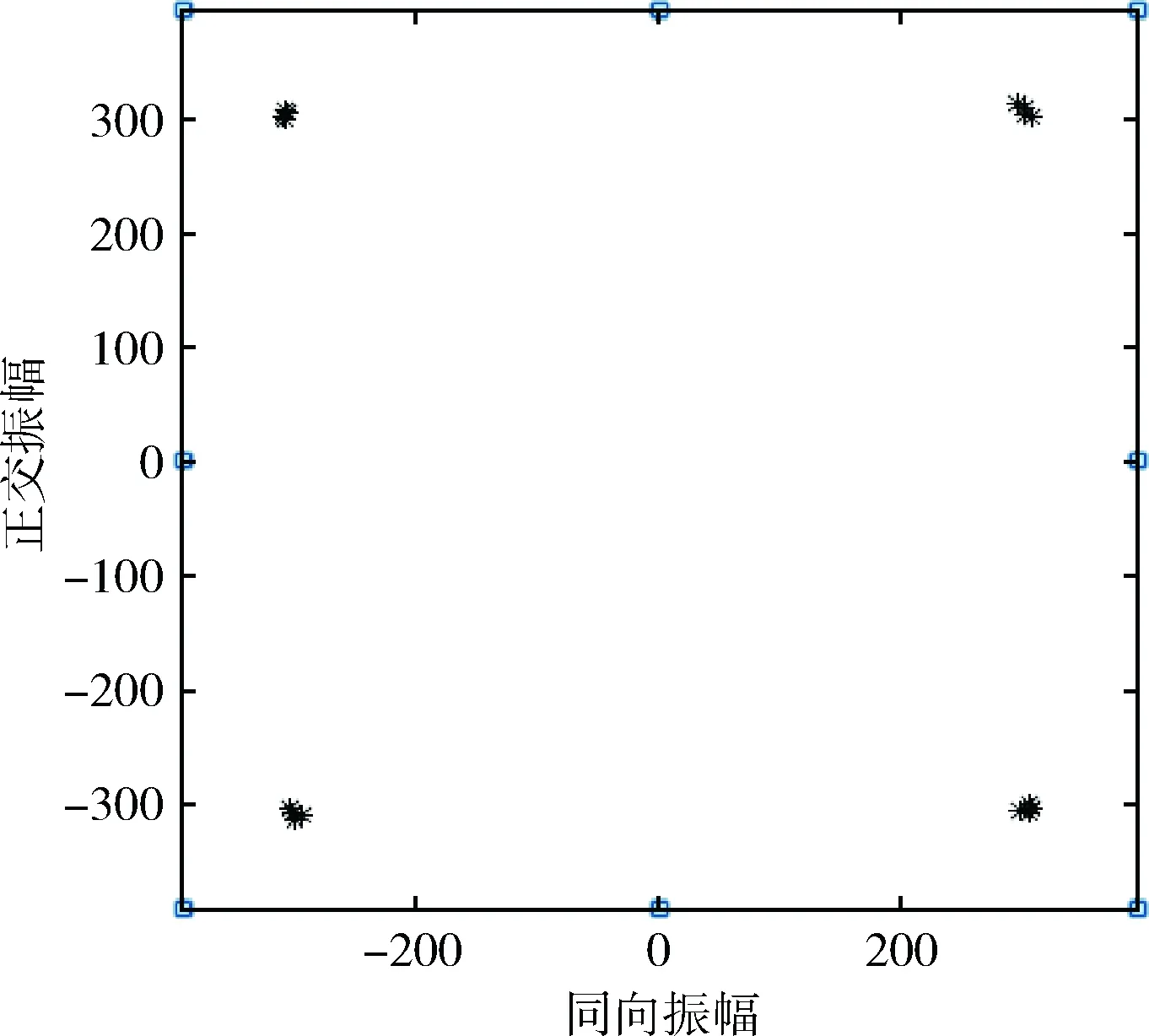
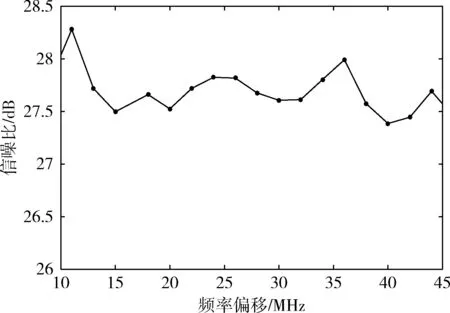
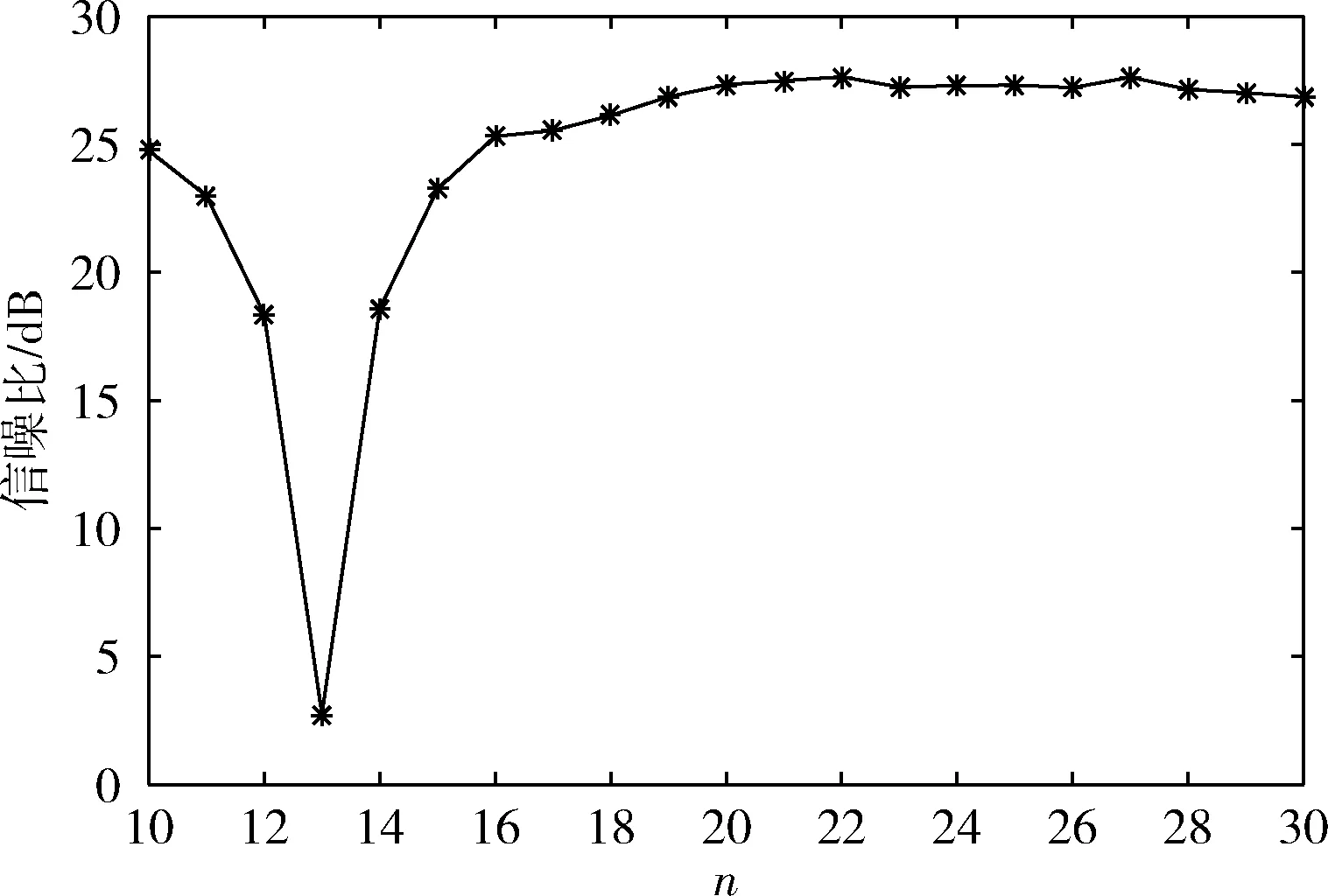
经过带通采样,所有索引为n的信号会映射到频率范围-B 图1 带通采样信号频谱 为实现软件无线电对多带通信号的无混叠接收,设计的系统应可同时接收不同频带上的多个射频带通信号,如图2所示,对多频段带通信号进行先采样、后分离处理,允许采样后在同一频段内有两个带通信号的频谱发生混叠,能够有效减轻模拟前端的负担。其中,二阶带通采样模块包括两路采样通道ADC A、ADC B和一个时钟发生器。两个ADC在操作时设置时延差TΔ以使得在两路ADC的采样信号中引入差异,在频域中则表现为相角的延迟。 图2 系统结构 若采样后的信号没有发生混叠,则对采样后的信号进行下变频转化为基带信号,并将多频段带通信号中的每个信号逐一分离;若采样后在同一频域内有两个信号发生混叠,则进行以下分析处理: 定义采样后发生混叠的两个信号分别为R0(f) 和R1(f), 第一、第二采样流之间的时延差为TΔ;两个信号经过第一采样流采样后的频谱为RA(f), 经过第二采样流采样后的频谱为RB(f);RB(f) 和RA(f) 满足关系 (2) 式中: (n-1/2)fs<|f|<(n+1/2)fs, 设β=e-j2πΔTfs, 则RB(f)=R0A(f)βn0+R1A(f)βn1, 其中,n0和n1分别为R0(f) 和R1(f) 在频率区域中的位置索引值。 二阶采样模块得到的两路数字信号经过设计的抗混叠滤波器实现混叠消除。将抗混叠滤波器SA(f) 和SB(f) 设计并分别应用于通道A和通道B。于是恢复的信号频谱变为 R(f)=B·[SA(f)·RA(f)+SB(f)·RB(f)] (3) 通过拆分信号的正频谱和副频谱,式(3)以变换为 R(f)=B·[SA(f)·(RA+(f)+RA-(f))+ (4) 对每路通道来说,都存在来自n0和n1频率位置的信号,因此,式(3)以进一步分解为 R(f)=B·[SA(f)·(R0A+(f)+R1A+(f)+R0A-(f)+ (5) (6) 和 (7) 式中:C为信号的幅值增益。这里选择SA(f) 为最简单的形式,即 (8) (9) (10) 式(8)~式(10)为滤波器在频域内的表达式,通过式(8)~式(10)以得到它们的脉冲响应,得出滤波器脉冲响应为 (11) (12) (13) 其中,fl、fh分别为抗混叠滤波器的最低频率和最高频率。通过对待采样信号以fs=2B进行采样,得到采样值用来作为抗混叠滤波器的参数。当信号位置索引发生变化时,仍可以采用同一SA。 但是对于SB, 当位置索引发生变化时,需根据位置索引对滤波器参数进行调整。 由于抗混叠滤波器的原因,恢复后的信号与原始信号具有一定的幅值差异,将式(8)、式(9)带入式(6)可得出幅值增益的表达式如式(14)所示 (14) 由式(14)可知,根据n0,n1的位置来实时调整TΔ的值可以得到较好的增益效果。 二阶带通采样模块的采样频率应当遵循以下公式 (15) 本文所提出的二阶带通采样抗混叠接收器通过MATLAB Simulink仿真模型实现,如图3所示。待处理的多频段射频带通信号通过两路设有时延差的采样流进行二阶带通采样,形成两路具有相位差的采样后信号,利用相位差设计抗混叠滤波器,从而实现对两混叠信号的分离。 图3 仿真模型 设置采样频率fs=100 MHz, 根据文献[16],设置原始时延TΔ=0.4 ns时,二阶带通采样在硬件实现中可行。 测试输入的两个信号分别具有中心频率fNca=2.025 GHz,fNcb=1.330 GHz。 用信号位置索引的定义可知n0=20,n1=13。 经过带通采样,两个信号被同时接收,频谱如图4所示。在带通采样之后,两个信号的中心频率分别是25 MHz和30 MHz。由图4可知,采样后的两个带通信号相互重叠。 图4 带通采样信号频谱 基于抗混叠滤波算法,在MATLAB中利用FDA工具设计抗混叠滤波器。通过二阶带通采样并在两路采样流之间设计时间延迟,以及根据式(8)~式(10)设计抗混叠滤波器,第一路信号可以被恢复为如图5所示,即由第二路信号引起的混叠被抑制。同样地,设计滤波器以抑制第一路信号可以分离出第二路信号,如图6所示。 图5 抗混叠滤波处理后第一路信号频谱 图6 抗混叠滤波处理后第二路信号频谱 在第一路获取恢复的带通信号之后,执行数字下变频和解调以恢复信号,图7是当输入RF信号为1.330 GHz时重构信号的星座图,信噪比SNR为27.8243 dB。 图7 重建信号星座 为了分析固定位置n时不同频偏下的信号重构效果,固定fNca=2.025 GHz, 实验测量了n1=13时频率偏置为10 MHz~45 MHz下的信噪比SNR,结果显示重构性能至少达到27.4 dB的SNR,如图8所示。 图8 不同频率偏置处的SNR 为进一步分析重构信号的性能,继续实验测试第一路信号在不同位置索引处的接收效果,固定一路信号n0=20, 测试了位置n1=10~30处的信噪比SNR,如图9所示。 图9 不同位置n1处的SNR 根据一系列实验结果可以看出,当位置n1分别为10,12,14,16时对应的SNR为24.7636 dB,18.3612 dB,18.5735 dB,25.3147 dB,效果较差。根据式(14),可以通过增加延迟TΔ的方法提高接收信号增益,将TΔ调整为1.8 ns时进行测试,结果表明,在n1=10,12,14,16时信噪比被分别提升到了27.2691 dB,27.1592 dB,27.1532 dB,27.3592 dB。因此,根据信号位置实时调整延迟TΔ可以提高系统性能。 针对采样后信号混叠的问题,提出了一种基于二阶带通采样的抗混叠滤波算法,在理论分析的基础上对所提出的相位调整滤波算法进行了仿真验证,仿真结果表明该抗混叠滤波算法可以有效实现两路混叠信号的分离,并且在接收过程中不需要针对不同位置的信号频繁变更采样频率,简化了模拟前端。最后通过仿真对信号的重构进行了性能分析,在固定位置n时可以实现至少27.4 dB的SNR,信号具有较好的恢复效果,此外还验证了可通过调整延时差来改善信号的重构性能。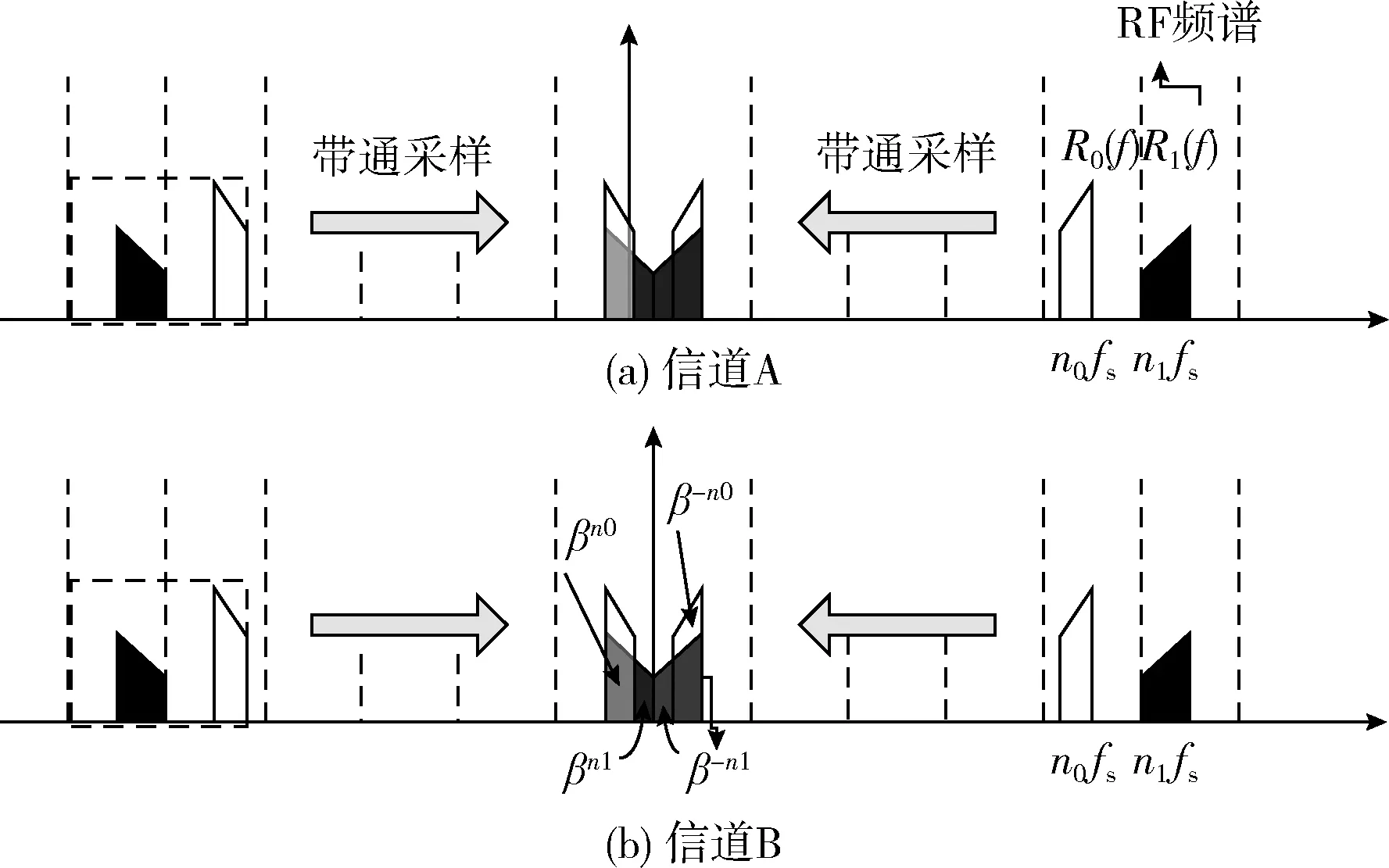
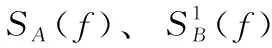
2 抗混叠滤波器
2.1 抗混叠滤波器的设计
SB(f)·(RB+(f)+RB-(f))]
R1A-(f))+SB(f)·(R0B+(f)+R1B+(f)+
R0B-(f)+R1B-(f))]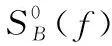
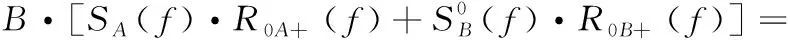
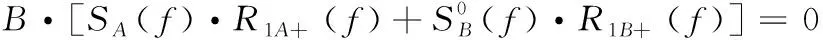
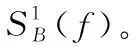
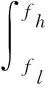
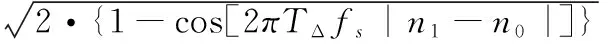
2.2 约束条件
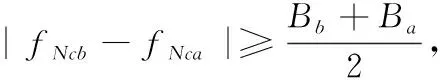
3 仿真分析
3.1 抗混叠滤波处理结果
3.2 信号的重构分析
3.3 不同位置时的信号重构性能分析
4 结束语

