三维针刺C/C控制棒导向管侧向抗压强度评价的数值研究

管月霞 刘新宽 曾广礼 高彦涛

1（上海理工大学材料科学与工程学院 上海 200093）

2（中国科学院上海应用物理研究所 上海 201800）

C/C复合材料具有导热性好、耐腐蚀性好、承载能力强等优点［1］。该材料被广泛应用于航空航天、汽车工业、核能等多个领域。三维针刺C/C复合材料是由碳基体与针刺预制体复合而成。它比三维编织复合材料的制备工艺更简单，密度更大，是一种具有广阔应用前景的耐高温结构复合材料。但三维针刺C/C复合材料构件的力学性能对几何形状、预成型结构非常敏感。在实际的制造、使用和维护过程中，往往要承受各种外部载荷，这会导致内部损伤产生，严重影响复合材料在使用过程中的性能，降低了复合材料构件的使用寿命。所以有必要对复合材料的极限承载力和渐进损伤行为进行研究。

研究渐进损伤行为需要模拟复合材料从初始损伤到最终失效的逐渐失效过程。Mei［2］对陶瓷基复合材料进行了压缩加载试验和卸载试验，分析了复合材料不同损伤机制对材料性能影响的差异性；Cai［3］对三维针刺C/C复合材料进行了三点弯曲加载试验，在弯曲载荷作用下进行了力学表征和微观结构的观察，结果表明：该材料具有假塑性断裂特征，平均强度为120 MPa；温卫东［4］着重考虑了复合材料基体开裂、层间剪应力以及层间拉应力等因素对材料在低速冲击下产生分层损伤的影响，并发展了一种可以判断复合材料层合板分层失效的准则。通过试验对复合材料失效过程的研究，可以发展一种评估复合材料渐进损伤的有限元计算方法。

有限元方法（Finite Element Method，FEM）是工程计算的重要手段之一，即使在复杂的工程结构中也可以用有限元方法进行分析［5］。由于复合材料在载荷作用下会产生多种应力状态，因此有限元方法特别适合于分析复合材料的渐进损伤。Lee［6］在用有限元方法去分析复合材料损伤方面具有突出贡献，最早使用三维有限元程序来分析复合材料的层合板失效；Chang［7］是最先提出含孔层合板在载荷作用下的渐进损伤计算模型的学者之一。他对层合板的损伤机理和破坏过程都进行了分析，并得到了与试验结果吻合较好的计算结果；Reddy和Pandey［8］采用了第一层失效的判定原理对复合材料层合板进行了失效分析；Hwang和Sun［9］对复合材料层合板建立了三维有限元损伤模型，用改进过的Tsai-Wu强度张量理论对层合板进行失效预测并根据不同的失效机制对失效的刚度进行了折减。

在工程应用中，C/C复合材料除了有简单的层合板外，还有管状结构和其他复杂的结构。近年来，人们开始对复合材料薄壁圆管的压缩破坏模式和机理进行研究。Hull［10］对复合材料薄壁圆管进行了轴向压缩试验，将其产生的破坏模式分为开放模式和破碎模式，并分析了不同破坏模式下的破坏机理；Jackson［11］对碳纤维复合材料的薄壁圆管进行了准静态压缩试验，试件呈现出开放的压缩破坏形态。在轴向压缩作用下，试件在管壁中部产生了破裂，并伴有碎片产生。

日本原子能机构（Japan Atomic Energy Agency，JAEA）一直致力于高温反应堆的研究，高温反应堆中的工作温度能够达到1 000℃以上，会大大降低控制棒材料的蠕变强度。为了提高控制棒的使用寿命，JAEA选择C/C复合材料作为控制棒的候选材料［12-13］。2012年，中国科学院启动了钍基熔盐反应堆（Thorium Molten Salt Reactor，TMSR）核能系统的研究项目，该项目的目标是研发第四代熔盐反应堆（Molten Salt Reactor，MSR）［14-15］。钍基熔盐反应堆中运用的金属控制棒导向管存在蠕变强度退化和熔盐腐蚀等问题，为了提高钍基熔盐反应堆的安全性需要开发新的控制棒导向管材料。参考JAEA的工作，考虑使用C/C复合材料作为钍基熔盐堆控制棒导向管的候选材料。为了评估三维针刺C/C复合材料作为钍基熔盐反应堆控制棒导向管的可能性，本文计算了不同尺寸三维针刺C/C导向管的极限承载能力。首先，对导向管进行了准静态侧向压缩试验，然后利用ABAQUS软件对整个试验过程进行建模和仿真，并编写了USDFLD子程序来实现侧向压缩过程中材料属性的衰减。通过试验结果与模拟计算结果的对比，建立了三维针刺C/C导向管强度和极限承载力的预测模型。在此基础上，运用提出的预测模型分析了不同直径和管壁厚度对三维针刺C/C导向管力学性能的影响。

1 渐进损伤理论

复合材料有复杂的破坏行为，受纤维和基体的组成、纤维含量、孔隙特征和载荷类型等因素的影响，基本的失效模式包括纤维断裂、纤维屈曲、基体开裂、层间分层和界面粘结失效等［16-17］。最大应力理论、最大应变理论、Hashin失效准则是常用的三种评估复合材料损伤的理论［18-19］。虽然这些理论提供了评估破坏模式的方法，但它们并没有解决复合材料的相互作用效应。Tsai和Wu［20］建立了适合各向异性材料损伤失效的Tsai-Wu强度张量理论。Tsai-Wu强度张量理论考虑了复合材料在破坏时的各种应力状态。该理论最重要的特点是将相互作用项作为独立分量，满足坐标变换的不变性要求，考虑了正应力和负应力的强度差异和复合材料的对称性［21］。根据三维针刺C/C复合材料是各向异性材料，本文计算时采用Tsai-Wu强度张量理论。

1.1 Tsai-Wu强度张量理论

在Tsai-Wu强度张量理论中，各向异性材料的强度可以从结构的承载能力来估计。强度准则的基本假设是在应力空间中存在一个破坏面，其形式为：

式中：σi，σj，σk为应力向量；Fi，Fij，Fijk表示材料属性的强度系数，并且σ4=τ23，σ5=τ32，σ6=τ12。

对于式（1），取前两阶可得：

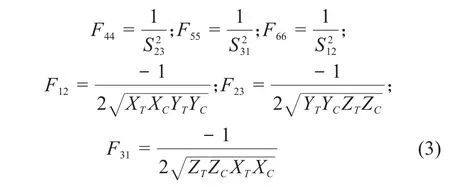
式中：XT为横向抗拉强度；XC为横向抗压强度；YT为纵向抗拉强度；YC为纵向抗压强度；ZT为厚度方向抗拉强度；ZC为厚度方向抗压强度；S为剪切强度。

1.2 材料参数损伤退化

当复合材料受到损伤时，需要根据试验结果设定退化方案去降低材料的刚度。如果在整个分析过程中使用恒定的材料刚度，计算结果将是不准确的。在大多数复合材料的渐进损伤分析模型中，材料的弹性常数根据材料的破坏模式特点而直接降低，即刚度折减方法［22］。刚度折减方法与其他方法相比更容易实现计算并且拥有较高的准确度。本文编写了一个ABAQUS材料用户子程序USDFLD来描述材料的性能退化。在损伤模型中，折减系数是一个非常重要的参数。若系数选取不当，将导致材料退化刚度矩阵出现奇异性，最终导致仿真计算无法收敛而终止。折减系数Di（i=1，2，…，9）降低损伤单元刚度的方法如下：

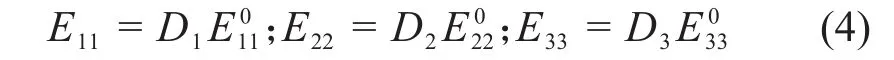
式中：E11为折减后的模量；E011为未损伤模量。各失效模式对应的材料刚度折减方案如表1所示。

表1 失效模式和刚度折减Table 1 Failure mode and the reduction of material stiffness

2 压缩试验

主要介绍三维针刺C/C导向管准静态侧向压缩试验过程，试验是在美国MTS公司的压缩测试仪（E44.204）上进行。试验时使用的三维针刺C/C复合材料由无纬碳布、预制短纤维和针刺纤维组成。一层碳布和一层预制体连续叠加，相邻的碳布层互为90°。三维针刺C/C复合材料的体积密度约为1.8 g∙cm-3，纤维体积分数约为40%，层厚为0.625 mm。三维针刺C/C复合材料在厚度方向具有不同的性能，但在其他两个方向上具有相同的性能。钍基熔盐堆设计的导向管内径为130 mm，外径为150 mm，本文试验根据钍基熔盐的设计，不改变半径和厚度尺寸，长度定为150 mm。图1（a～d）为三维针刺C/C导向管准静态侧向压缩过程。导向管固定在两个刚性圆盘之间，下盘固定，上盘垂直向下移动。上部圆盘的加载速度设定为0.50 mm∙min-1，因为加载速度较慢，所以可视为准静态过程。由图1（a）可以看出，在位移加载开始时，导向管只有轻微变形，没有损伤。随着压缩的继续，图1（b）的标记部分开始出现裂纹并开始破裂（由放大处可知）。再进一步加载后，导向管的两侧开始出现裂纹，如图1（c）所示。当导向管破裂失效时试验停止如图1（d）所示。通过对试验过程的观察，发现三维针刺C/C导向管的抗压性能优于抗拉性能，这是脆性材料的一种常见性能。

图1 导向管压缩断裂过程Fig.1 Fracture process of guide tube

图2为导向管侧向压缩过程中承载能力的变化图。在初始阶段，载荷和位移几乎呈线性关系。这表明，导向管处于弹性变形阶段。随着位移的继续加载，载荷的增长变缓慢，载荷与位移变为了非线性关系，此时基体裂纹首先出现并继续扩展。当加载位移为4.16 mm时，导向管的载荷达到极限值15.29 kN，达到极限承载能力之后导向管进入失稳状态。最终由于脱层和纤维束的脱附，曲线呈阶梯状下降［23］。

图2 导向管压缩过程中的载荷-位移Fig.2 Load-displacement of guide tube during compression

3 数值研究

讨论了用于评估三维针刺C/C导向管强度的计算模型。采用了有限元方法，用ABAQUS软件模拟准静态侧向压缩试验过程，分析比较试验结果和计算结果，验证三维针刺C/C管损伤模型的可行性。

3.1 线性分析

三维有限元程序堆导向管的失效分析为C/C复合材料在TMSR中的应用提供了一种新的评价方法。首先使用ABAQUS软件对导向管进行建模。有限元模型中使用的三维针刺C/C复合材料力学常数如表2所示。

表2 三维针刺C/C复合材料的力学常数Table 2 Mechanical constants of 3D needle-punched C/C composite material

导向管的有限元侧向压缩模型如图3（a）所示。在ABAQUS软件计算中，底部刚性圆盘下表面设定为固定边界条件，上部刚性圆盘以0.008 mm∙s-1的速度进行位移加载，当模拟时间到达1 500 s时压缩停止。图3（b）为线性有限元模型得到的位移-荷载曲线与压缩试验结果对比图。结果表明：在初始阶段两条曲线吻合良好，计算结果较为保守。随着位移加载的继续，线性计算结果慢慢偏离了试验结果。因此，本模型只能预测导向管在弹性变形下的压缩情况，无法预测导向管的极限强度。为了准确地预测导向管在压缩时的破坏过程，需要在材料达到破坏时对其刚度进行衰减，通过编写USDFLD用户子程序可以解决此问题［24］。用户子程序是利用Tsai-Wu强度张量理论和刚度折减方法对导向管的强度和破坏过程进行了数值模拟。

图3 导向管有限元模型(a)，模拟计算结果与实验结果对比图(b)Fig.3 Finite element model of guide tube FE(a),comparison diagram of simulation results and experimental results(b)

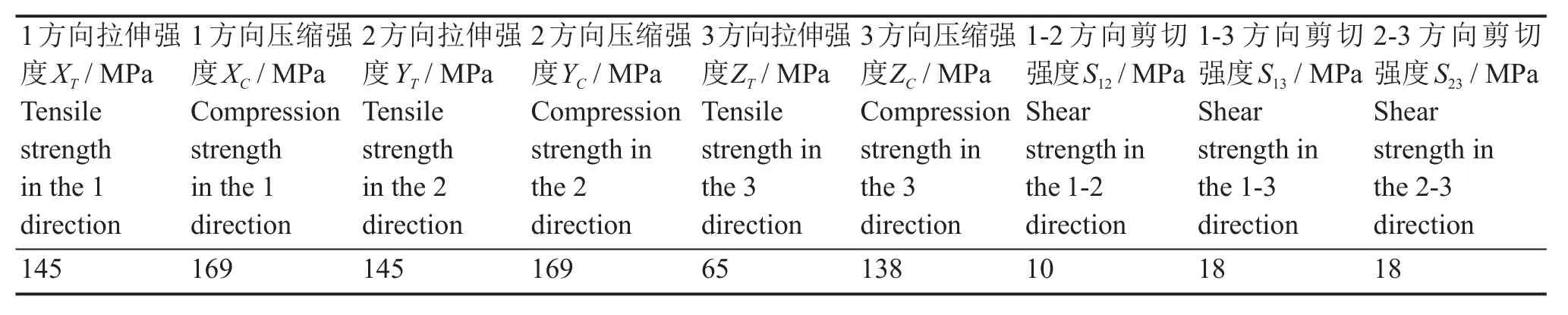
表3 三维针刺C/C复合材料的力学性能Table 3 Mechanical properties of 3D needle-punched C/C composite material

3.2 非线性分析

本节中导向管有限元压缩模型的边界条件与§3.1设定一致。式（3）中使用的材料参数如表3所示。图4（a）是导向管加载位移为12 mm时的位移图，可以直观地看到，导向管在压缩后的位移分布情况，导向管左右两侧的位移变化呈对称性。图3（b）为侧向压缩下的变形过程。对于准静态和低速破碎过程来说，结构上下部位的变形是对称的［25］。

计算时模型选择的网格单元类型为C3D8，考虑到网格密度对计算结果有很大的影响，计算了不同尺寸网格的模型。网格划分过于密集，模型计算时间将呈指数增长。在保证计算精度的前提下，继续增加网格密度不会使计算精度提高太多。为了确定合适的材料网格尺寸，分析中使用了6 mm、5 mm、4 mm和3 mm网格尺寸，计算结果如图5（a）所示。从图5（a）中可以看出，不同网格的计算结果与试验结果的变化趋势基本一致。计算结果均低于试验值，说明预测结果较为保守。随着网格尺寸的减小，计算结果趋于收敛，网格尺寸为3 mm时的结果与试验数据最吻合。网格尺寸设定为3 mm，位移加载时间为535 s时导向管失效。此时的加载位移为4.28 mm，承载能力达到最大值14.01 kN，这与准静态侧向压缩试验结果非常接近。当达到极限荷载时，导向管破坏，其承载力开始下降，与试验结果一样曲线呈阶梯状下降趋势。一般来说，试验数据与计算结果之间存在一定的误差。理论和试验结果之间的差异有几个来源，包括试验误差、失效预测方法的误差和材料的可变性。从图5（a）可以很容易计算出极限承载力之间的误差，当网格尺寸从6 mm减小到3 mm时，误差从22%减小到8%。一般认为当误差小于10%时是可以接受的。因此，当网格尺寸为3 mm、误差为8%时，该计算结果是可被接受的。在保证计算结果准确性的计算模型下，继续减小网格尺寸不仅会增加大量的计算时间还提高了成本。

导向管的应力分布也是评价损伤的重要内容。图5（b）为导向管在压缩加载过程中上部内侧面的轴向应力图。由于刚性圆盘加载在导向管的轴向中间部位，因此曲线具有对称形状。图5（b）中两个峰值点是圆盘边界与导向管之间的接触点，达到了61.50 MPa。峰值处的应力比复合材料管两端的应力高了近50%，出现应力集中的现象。应力集中不能通过塑性变形来松弛，大大降低了构件的强度，尤其在脆性材料制成的构件中，应力集中现象会一直保持到峰值应力达到强度极限之前，从而最终导致构件发生脆性破坏。在工程应用中，应力集中问题是我们首先要考虑的，此处的断裂可能会导致整个构件的失效。

图6（a～c）为导向管失效过程中的应力云图。从图6（a）可以看出，导向管上下部内壁最大主应力大于外壁最大主应力，两侧的内壁最大主应力小于外壁的最大主应力。在图6（a）中，箭头所指的位置表示峰值应力点，是损伤首先发生的位置。导向管失效后的应力图如图6（b）所示。图6（c）是图6（a）的解剖应力图，可以更直观地观察到箭头所指部位的应力分布。导向管每一层的应力是不同的，由外往内应力不断增大。

图6（a）中上部箭头所指部位在压缩过程中应力随时间变化曲线如图7（a）所示。该点的应力在A点前呈线性上升趋势，然后上升速度减缓。在B点时，应力达到最大值159.32 MPa。随着位移加载的继续，应力迅速减小，直至降为零。图7（b）为该点的应力-应变图。从图7（b）可以看出，应力-应变曲线在C点之前是线性关系，说明材料的刚度保持不变，符合胡克定律。当材料被发生破坏时，应力-应变曲线的斜率减小，表明刚度开始减小。三维针刺C/C复合材料是一种脆性材料。对于脆性材料，压缩时的应力-应变曲线是非线性曲线延展性一般小于0.5%，断裂前变形很小。模拟结果与脆性材料的性能吻合较好。刚度是物体抵抗变形的能力，表示为：图7（c）为位移加载时导向管的刚度变化图。材料断裂前，刚度保持在50 280 MPa，这与给定的材料参数是一致的。然后压缩继续，材料开始断裂，刚度降低。刚度降低的速度越来越快，当整个构件失效时，材料的刚度降低到0。

图4 导向管压缩过程中位移变化(a)和变形(b)Fig.4 Guide tube displacement(a)and deformation(b)during compression

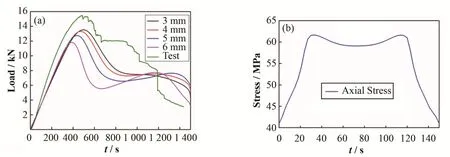
图5 不同尺寸网格的计算结果与实验结果对比(a)和轴向应力分布(b)Fig.5 Comparison of calculation results and experimental results of different meshes(a),axial stress distribution(b)

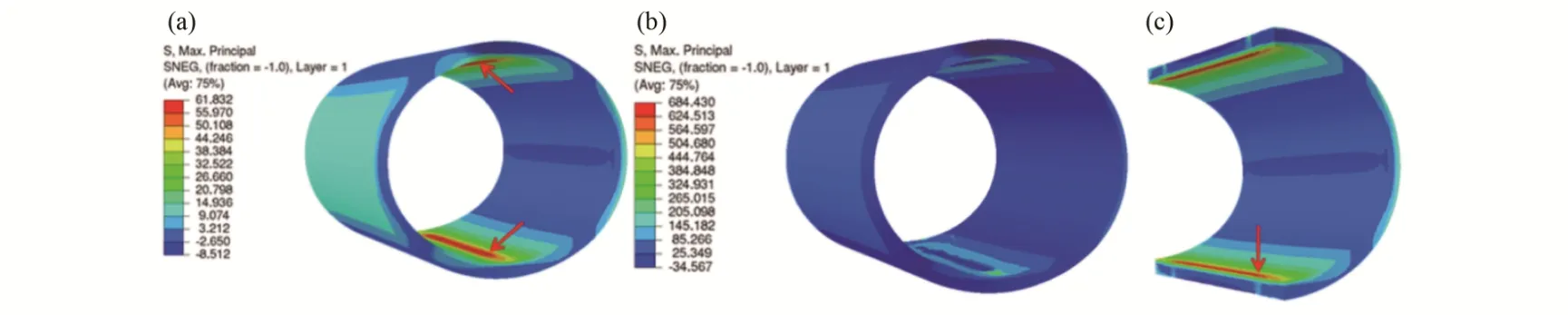
图6 导向管失效前(a)、失效后(b)和失效前解剖(c)应力云图Fig.6 Stress distribution of guide tube before the failure(a),after the failure(b),and pre-failure dissection(c)

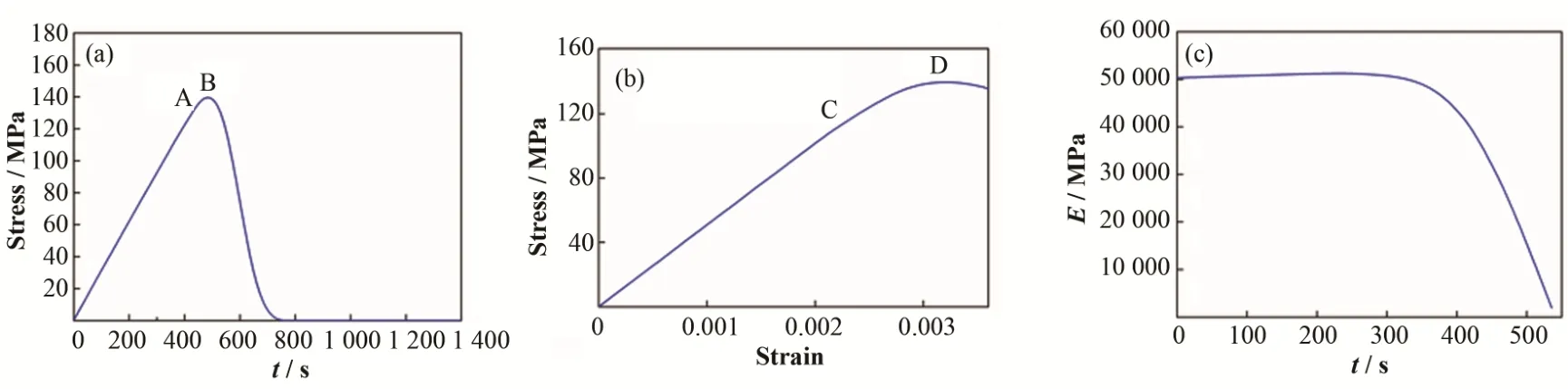
图7 应力峰值点的应力随时间变化(a)、应力-应变曲线(b)和刚度变化(c)Fig.7 Stress changes with time(a),stress strain curve(b)and stiffness changes with time(c)of peak stress point

3.3 不同直径和厚度的影响

为了进一步了解不同直径和厚度对导向管极限承载能力的影响，利用三维有限元损伤模型对多种尺寸的导向管进行仿真模拟。三种不同直径的导向管分别为 ø180 mm（内径）×ø200 mm（外径）×150 mm（长度）、ø130 mm（内径）×ø150 mm（外径）×150 mm（长度）和ø80 mm（内径）×ø100 mm（外径）×150 mm（长度）。计算结果如图8（a）所示，当导向管的外径为100 mm，压缩位移为2.36 mm时，导向管失效，极限载荷为23.77 kN。对于外径为200 mm的导向管，直到压缩位移加载到6.20 mm时才失效，并且极限承载能力下降至8.82 kN。导向管的极限承载能力随管径的增大而减小，但能够承受的变形增大。

继续预测了不同管壁厚度对导向管承载能力的影响。导向管外径尺寸为150 mm，管材厚度分别为5 mm、10 mm、15 mm。由图8（b）可知，当管壁厚度为5 mm时，导向管的极限承载能力仅为3.26 kN。当管的厚度增加到15 mm时，极限承载能力激增到32.90 kN。随着管壁厚度的增加，导向管的极限承载能力迅速增大，但导向管管壁厚度增大后仅能承受较小的变形。

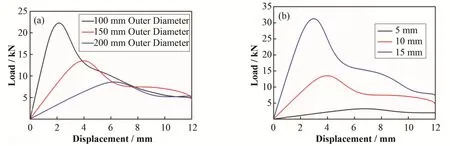
图8 不同直径(a)和不同管壁厚度(b)的计算结果Fig.8 The calculation results of different diameters(a)and thicknesses(b)

通过以上的讨论，我们可以发现直径和厚度这两个因素对导向管的极限承载能力和抵抗变形能力有很大的影响。当三维针刺C/C导向管应用于TMSR或其他工程中时，应着重考虑这两个方面。本文建立的三维失效破坏模型能有效地预测三维针刺C/C导向管的渐进破坏过程，为C/C复合材料的工程应用和设计提供了一定的参考价值。

4 结语

本文对三维针刺C/C导向管的渐进损伤过程进行了分析研究，得到以下三点结论：

1）采用准静态侧向压缩法研究了先进核材料三维针刺C/C导向管的力学性能。试验得到了位移与荷载之间的关系。结果表明：三维针刺C/C导向管的极限荷载达到了为15.29 kN。

2）提出了一种模拟导向管侧向压缩过程的先进有限元方法。本文选取的Tsai-Wu强度张量理论适用于损伤模型。USDFLD子程序中的折减系数也是恰当的。当计算3 mm的网格时，加载位移为4.28 mm时，导向管失效，其极限荷载为14.01 kN，与试验结果误差仅为8%。

3）通过对不同直径和不同厚度的导向管进行了预测和分析，发现直径和厚度这两个因素对导向管的极限承载能力有很大的影响。在不影响使用效果的情况下，应当设计直径较大，管壁厚度较厚的管状构件。