城轨交通换乘站结点换乘设施行人拥堵分析方法
何 彬,顾保南,杨 照
(1.同济大学道路与交通工程教育部重点实验室,上海201804;2.上海市轨道交通结构耐久与系统安全重点实验室,上海201804)
城市轨道交通车站站内的行人设施包括出入口通道、换乘通道、安检仪、检票闸机、楼梯、自动扶梯以及可供行人走行的站厅、站台空间。在规划设计阶段,上述要素存在许多可能变化,因而可形成诸多可能的行人设施布置方案。
由于行人流微观仿真并不适用于大量方案的快速生成与评价,为了在规划设计阶段实现大量方案的快速生成和评价,部分国内研究人员提出了“网络法”[1-6]。目前最具可操作性的“网络法”是郭长弓等[5-6]提出的行人流线网络法。该方法将列车车门和车站出入口视为客流起讫点,把安检通道、闸机组、楼梯、自动扶梯等行人设施以及设施间的各股行人流抽象为边,把站内易拥堵区域抽象为实结点,仅起连接作用的点称为虚结点,形成了行人流线网络。然后,针对闸机组前区域、梯组前区域以分时段客流迭代为核心建立了实结点模型。最后通过行人流线网络客流分配得到易拥堵区域的客流密度、拥堵面积等指标用于拥堵判定。
但是,结点换乘设施尚未被所考虑,其由一个位于上下两层站台间的平台以及连接平台与站台的2-4部楼梯组成,行人可以通过其完成上下层站台间的直接换乘。
与闸机组前区域、梯组前区域不同,结点换乘设施在客流进出换乘平台时存在合流和分流现象,随着结点换乘设施形式不同,换乘平台内存在2-8个方向客流的交织冲突,并且客流在由本线站台经过结点换乘设施到达他线站台的过程中,始终受到前方设施客流状态的影响,即:换乘平台的客流状态影响着由楼梯进入换乘平台的客流状态,楼梯客流状态影响着由换乘平台进入楼梯的客流状态以及由梯前区域进入楼梯的客流状态。上述情况在既有实结点模型中均未予以考虑。另外,结点换乘设施在进行行人拥堵分析时,可能涉及多达8个断面的客流通过情况,较闸机组前区域和梯组前区域的情况更为复杂。如果不针对结点换乘设施的上述特点提出相应的方法或模型,行人流线网络法的普适性将会受到影响。更为重要的是,现行的地铁设计规范[7]中没有给出结点换乘设施能够承受的客流需求量级,使其设计在一定程度上缺乏指导。目前,专门针对结点换乘设施的研究成果极少,文献[8]以南京地铁新街口站的结点换乘设施为案例验证其提出的交通瓶颈拥堵概率确定方法的可行性。其他文献仅将其作为一种换乘方式简述其形式,例如,丁园园[9]将结点换乘设施分为十字型、T型和L型。因此,有必要提出结点换乘设施行人拥堵分析方法。
1 研究对象
由于结点换乘设施变化较多,本文以图1所示的“十”形结点换乘设施(以下简称“设施”)为研究对象。
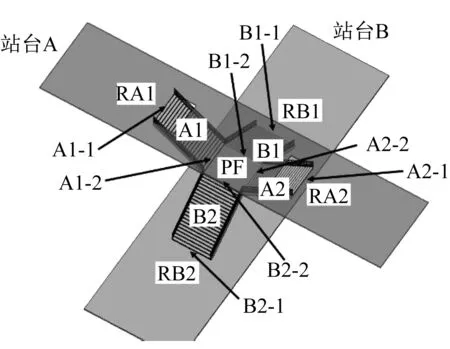
图1 “十”形结点换乘设施Fig.1 Crisscross node transfer facility
如图1所示,PF表示换乘平台,A1、A2、B1和B2表示楼梯,4部楼梯的中线向换乘平台内部延伸可形成一个正“十”形。楼梯A1和楼梯A2与上层站台(站台A)相连,楼梯B1和楼梯B2与下层站台(站台B)相连。四部楼梯和换乘平台内均不设置分隔栏杆。A1-1、A2-1、B1-1和B2-1为楼梯与站台的分界断面,A1-2、A2-2、B1-2和B2-2为楼梯与换乘平台的分界断面。换乘客流由各车门到达楼梯与站台的分界断面后若不能及时进入楼梯,则在各自楼梯对应的梯前区域RA1、RA2、RB1和RB2内等待。
2 拥堵分析方法
以换乘平台在客流集散全过程中的平均密度和最大密度表征设施拥堵情况。
上述指标随着客流集散一直变化,这里将整个集散过程切分为若干个等长的小的时段。利用设施客流的流密速关系分别计算每一个小的时段内各断面的上下行客流量,从而得到各小时段末的换乘平台客流密度。
2.1 输入条件
输入条件包括设施方案输入条件、客流输入条件和其他参数三类:
(1)方案条件包括站台A和站台B内任一车门中心至同站台的各梯组及结点换乘设施楼梯的距离、换乘平台的各项尺寸、设施楼梯宽度、设施楼梯的梯级与休息平台的个数、位置。
(2)客流条件包括两站台上各车门的下车换乘人数、4个方向列车(A线上下行、B线上下行)的到达时间差。
(3)其他参数包括车门的下车流量、站台客流速度以及楼梯上下行客流速度、换乘平台客流速度的待定系数等。
2.2 小时段切分
取4个方向列车中最早到达列车的开门时间为零时刻,然后以相等时段长度依次向后划分小时段,比如,从零时刻起增加一个时段长度为第1个小时段,从第1个小时段末增加一个时段长度为第2个小时段,依此类推,直至结点换乘设施内不再有客流为止。
小时段长度不应使结点换乘设施内任一楼梯断面的允许通过人数小于1人,若以规范中双向楼梯最小宽度2.4 m计算,小时段长度不应小于0.4 s。建议将小时段长度取为2~3 s较为合适。
2.3 梯前区域客流到达分布
假定进出站客流不使用结点换乘设施,设施客流来自于列车各个车门的换乘客流。换乘客流与列车到站时刻有着密切关系,客流分布相对较集中;如果换乘距离较长,由于乘客年龄、性别等差异,换乘客流的分布呈现逐渐分散的状态。
由于站内OD(origin-destination)表无法体现乘客年龄、性别等个人特征,主要考虑站台走行距离对梯前区域客流到达人数的影响。假设任一车门处的下车换乘乘客均选择距离自己最近的楼扶梯进行换乘,客流从邻近平台的各个车门迅速向梯前区域汇集,由于车门与楼梯的距离及换乘乘客人数的不同,造成了楼梯前区域客流的不均匀到达。
下面以梯前区域RA1为例说明任意时段客流到达人数的确定方法,该方法借鉴了文献[10]的部分方法。
图2为站台A楼梯A1一侧示意图,设车门a中心至断面A1-1中心的走行距离为La。

图2 车门a至断面A1-1距离Fig.2 Distance from door a to section A1-1
车门a的下车换乘人数为na,车门a的乘客到达断面A1-1需要时间,车门a下车客流的持续时间即车门a在时段以流量Q持a续到达断面A1-1中心,则第i时段车门a乘客到达断面 A1-1 的持续时间则第i个小时段内由车门a到达梯前区域RA1的乘客数为ta,iQa。若用连续整数对车门进行编号,假设有且仅有h个连续车门(车门编号由m至n)的下车换乘客流流向区域RA1,则第i个小时段内梯前区域RA1的到达乘客数为
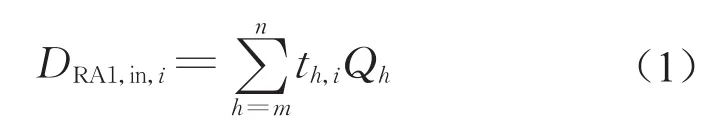
2.4 各断面客流通过客流量
从整个集散过程看,客流由换乘平台进入站台的过程中,其速度和流量一般不受站台客流状态的影响,但是客流由站台进入换乘平台的过程会受到换乘平台客流状态的影响,即速度存在关联关系,一般下面以下行客流为例进行说明:
(1)客流以一定速度通过楼梯到达换乘平台。
(2)客流开始持续进入换乘平台,使换乘平台密度由0逐渐增至KPF,dc。换乘平台内密度较低,各股客流均能够保持自由流状态。换乘平台客流速度始终大于楼梯下行速度,楼梯客流以自身下行速度持续进入换乘平台,梯前区域客流以相同速度进入楼梯。
(3)客流持续进入换乘平台,使其密度由KPF,dc持续增加至KPF,dm。在这一阶段中,换乘平台各股客流不再保持自由流状态,开始受到客流交织的影响,速度降低。某一时段后,换乘平台客流速度小于楼梯下行客流速度,楼梯客流转而以前者速度进入换乘平台。
(4)换乘平台密度达到KPF,dm并持续一段时间。换乘平台内没有多余空间,由楼梯进入换乘平台的流量降为0。换乘平台不再有乘客进入,而仍持续有乘客离开平台进入楼梯。
(5)换乘平台密度由KPF,dm逐渐下降,客流速度逐渐回升,相应的,进入平台方向的楼梯客流速度也逐渐回升,直至设施内乘客通过各部楼梯逐渐消散完全至站台为止。
梯前区域换乘客流对换乘平台密度变化的反应存在滞后性,即:由楼梯进入换乘平台的客流速度下降后,其通过流量也相应下降,但是楼梯整体客流速度不变,经过一段时间后楼梯客流密度持续增加,楼梯客流速度下降,由梯前区域进入楼梯的客流速度才随之下降。
各断面客流通过客流遵循上述过程,下面以梯前区域RA1下行客流为例,分别给出梯前区域RA1的下行客流经过各断面时的流量和通过人数计算方法。其他断面思路相同,不再赘述。
梯前区域RA1的下行客流首先经过断面A1-1进入楼梯A1,然后通过楼梯A1到达断面A1-2,然后分成两个分支,分别流向楼梯B1和楼梯B2,这里称这两支客流分别为客流A1-B1和客流A1-B2。客流A1-B1和客流A2-B1共同通过断面B1-2进入楼梯B1,而客流A1-B2和客流A2-B2共同通过断面B2-2进入楼梯B2。
(1)客流由站台经过断面A1-1进入楼梯
第i+1时段断面A1-1的下行通过流量为
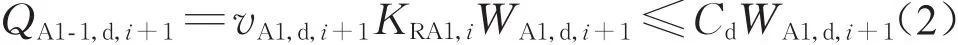
式中:vA1,d,i+1为第i+1 时段楼梯 A1 下行客流速度(m·s-1);KRA1,i为第i时段末,梯前区域RA1的客流密度(人·m-2);WA1,d,i+1为第i+1时段内楼梯A1的下行客流宽度(m);Cd为楼梯下行通过能力(人·(m·s)-1)。
结合郭长弓[5]、盛应平等[11]的研究,断面A1-1前存在一个矩形区域,该区域被占满前乘客在区域内均匀分布,被占满后会以密度KTQ,max向外扩展,因此有

式中:Lq为楼梯前乘客能够容忍的排队长度(m);WRA1,i为第i时段楼梯A1下行客流宽度(m)。
第i+1时段断面A1-1的下行通过人数为
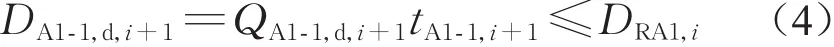
设TA1-1为梯前区域RA1客流开始到达的时刻,则tA1-1,i+1的取值见表1,其中ΔT为小时段长度。
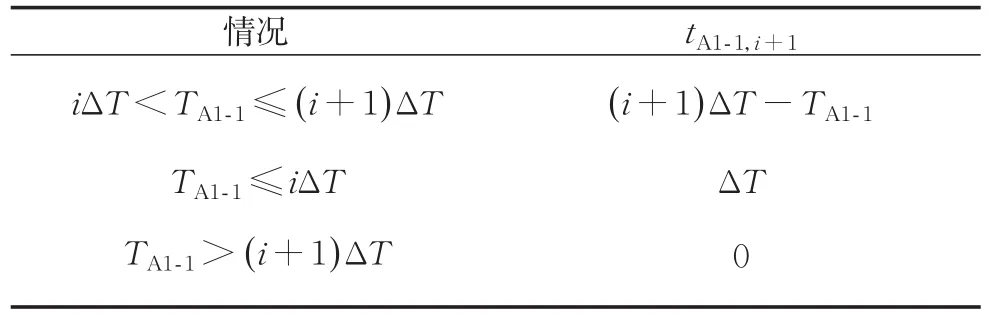
表 1 tA1-1,i+1取值Tab.1 Parameter value oftA1-1,i+1
(2)客流由楼梯经过断面A1-2进入换乘平台
客流经过断面A1-2时,客流速度受到换乘平台客流和楼梯A1下行客流的共同影响,即当客流A1-B1和客流A1-B2的客流平均速度vA1,B1+B2,i+1大于楼梯下行客流速度vA1,d,i+1时,楼梯下行客流以vA1,d,i+1持续进入换乘平台,否则,楼梯下行客流转而以vA1,B1+B2,i+1进入换乘平台。因此,第i+1 时段内,断面A1-2的下行通过流量为
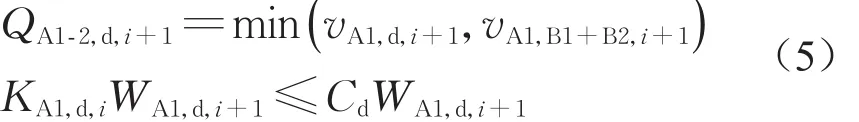
式中:KA1,d,i为第i时段末楼梯A1下行客流密度(人·m-2);vA1,B1+B2,i+1为第i+1时段客流A1-B1和客流A1-B2的平均速度(m·s-1),即
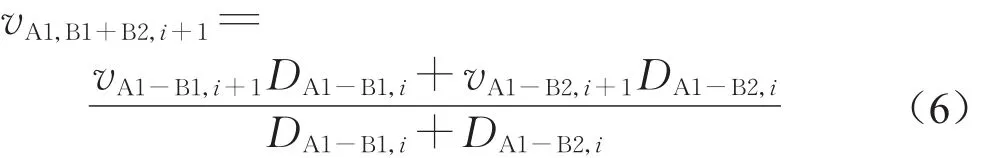
引入下行客流第i+1时段末在楼梯A1内的累计走行距离LA1,d,i+1用于判断下行客流是否通过断面A1-2。设LA1为楼梯A1的平面投影长度,当LA1,d,i+1≤LA1时,下行客流在第i+1 时段不通过断面 A1-2,QA1-2,d,i+1=0;当LA1,d,i+1>LA1时,下行客流在第i+1 时段通过断面 A1-2,QA1-2,d,i+1根据式(6)计算。
第i+1时段断面A1-2的下行通过人数为
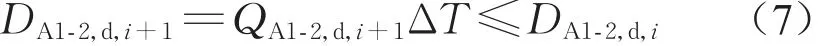
经过断面A1-2后DA1-2,d,i+1会分流至客流A1-B1和客流A1-B2,分流比例等于经过行人流线网络客流分配后得到的客流A1-B1和客流A1-B2的客流量之比,分别以αA1-B1、αA1-B2表示,具体分配方法见文献[12],不再赘述。
(3)客流A1-B1与客流A2-B1由换乘平台经过断面B1-2进入楼梯
客流由换乘平台进入楼梯时,受到换乘平台内客流A1-B1和客流A2-B1以及楼梯B1下行客流的共同影响,因此,第i+1时段内,断面B1-2的下行通过流量为
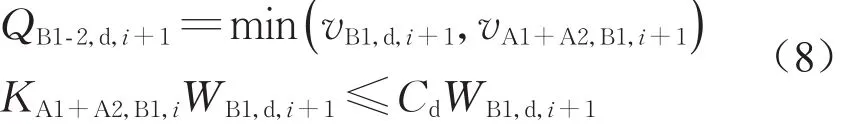
式中:vB1,d,i+1为第i+1时段内楼梯B1的下行客流速度(m·s-1);vA1+A2,B1,i+1为第i+1时段客流A1-B1和客流A2-B1的平均速度(m·s-1);KA1+A2,B1,i为第i时段末客流A1-B1和客流A2-B1的平均密度(人·m-2);WB1,d,i+1为第i+1时段内楼梯 B1 的下行客流宽度(m)。
设LA1-B1,i+1和LA2-B1,i+1分别表示客流 A1-B1和客流A2-B1第i+1时段末在换乘平台内的累计走行距离。LA1-B1和LA2-B1分别为下行客流开始通过断面A1-2和断面A2-2时客流A1-B1和客流A2-B1在换乘平台的预计走行距离。当LA1-B1,i+1≤LA1-B1且LA2-B1,i+1≤LA2-B1时,下行客流在第i+1时 段 不 通 过 断 面 B1-2,QB1-2,d,i+1=0;当LA1-B1,i+1>LA1-B1或LA2-B1,i+1>LA2-B1时,下行客流在第 i+1 时段通过断面 B1-2,QB1-2,d,i+1按式(8)计算。
假设楼梯A1和楼梯A2的下行客流于同时段开始通过断面A1-2和断面A2-2,该时段各部楼梯客流宽度如图3所示,E、F、G分别为断面A1-2、断面A2-2、断面B1-2下行部分的中点,则LA1-B1=|EG|,LA2-B1=|FG|。若客流开始通过断面A1-2或断面A2-2时楼梯B1内无下行客流,则取点G为断面B1-2中点。
第i+1时段断面B1-2的下行通过人数为

而客流A1-B1和客流A2-B1各自进入楼梯B1的人数占DB1-2,d,i+1的比例分别为同时分别不大于DA1-B1,i和DA2-B1,i。
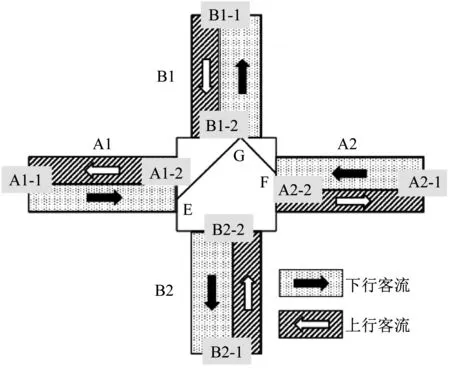
图3 换乘平台客流预计走行距离Fig.3 Expected distance of passenger flow on the transfer platform
(4)客流由楼梯经过断面B1-1进入站台
客流经过断面B1-1进入站台B的过程中,一般不受站台B客流影响,只受楼梯B1下行客流影响,则第i+1时段内断面B1-1的下行通过流量为

设LB1,d,i+1为下行客流第i+1 时段末在楼梯A1内的累计走行距离,LB1为楼梯B1的平面投影长度。当LB1,d,i+1≤LB1时,下行客流在第i+1 时段不通过断面 B1-1,QB1-1,d,i+1=0;当LB1,d,i+1>LB1时,下行客流在第i+1 时段通过断面 B1-1,QB1-1,d,i+1按照式(10)计算。
第i+1时段断面B1-1的下行通过人数为
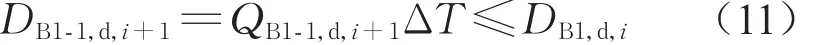
2.5 客流迭代过程
(1)令i=0,设零时刻结点换乘设施各部分客流密度、速度、各断面流量、各断面通过人数、设施滞留人数、客流宽度、客流占用长度等参数为0。
(2)判断客流是否全部离开结点换乘设施。若全部离开,则转(10);若没有,则转(3)。
(3)判断客流是否由车门到达梯前区域。若到达,则转(4),否则,仍设第i+1时段设施各部分客流密度、速度、各断面流量、各断面通过人数、设施滞留人数、客流宽度、客流占用长度等参数为0,转(9)。
(4)计算第i+1时段楼梯A1和楼梯A2的下行客流速度、楼梯B1和楼梯B2的上行客流速度,并计算上述客流的在第i+1时段末的走行长度。计算第i+1时段换乘平台各股客流速度,并计算第i+1时段末各股客流的走行长度。计算第i+1时段楼梯A1和楼梯A2的上行客流速度、楼梯B1和楼梯B2的下行客流速度,并计算上述客流在第i+1时段末的走行长度。转(5)。
(5)计算各楼梯的上下行客流在第i+1时段内的客流宽度。转(6)。
(6)根据之前得到的客流速度、客流密度、客流宽度计算设施各断面的上下行客流通过流量和客流通过人数。转(7)
(7)计算第i+1时段末各部楼梯的上下行客流滞留人数、换乘平台乘客滞留人数以及平台内各方向客流的滞留人数。转(8)。
(8)计算第i+1时段末各部楼梯的上下行客流滞留密度、换乘平台乘客滞留密度以及平台内各方向客流的滞留密度。转(9)。
(9)令i=i+1,转(2)。
(10)迭代结束,输出设施清空时间和换乘平台客流的平均密度和最大密度。
3 客流速度、宽度和占用长度计算
3.1 客流速度
(1)换乘平台客流速度
换乘平台内存在多个方向的客流,当换乘平台内客流密度较小时,由于客流具有自组织功能,有足够空间相互避让,对客流速度影响可忽略不计;当客流密度较大时,换乘平台内人均空间不足,客流相互之间无法避免交织冲突,对客流速度会产生较大影响。引用文献[13]的固定区域多向行人流速度模型,并结合设施特点,换乘平台内任一方向客流速度如下:
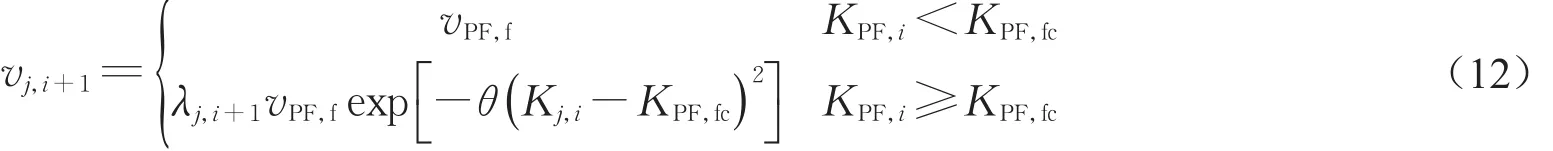
式中:j表示换乘平台内某方向客流,利用1-8这8个序号代表换乘平台内的8个方向的客流,具体见表2所示;vj,i+1为第i+1时段换乘平台内方向为j客流的速度(m·s-1);vPF,f为换乘平台客流的自由流速度(m·s-1);KPF,i为第i时段末换乘平台的客流密度(人·m-2);KPF,fc为换乘平台内客流是否为自由流的临界密度(人·m-2);Kj,i为第i时段末换乘平台内客流j的密度(人·m-2);θ为待定系数,θ>0;λj,i+1为第i+1时段内换乘平台内客流j速度相对于vPF,f的折减系数,见式(13)。

表2 换乘平台客流方向Tab.2 Passenger flow directions at a transfer platform
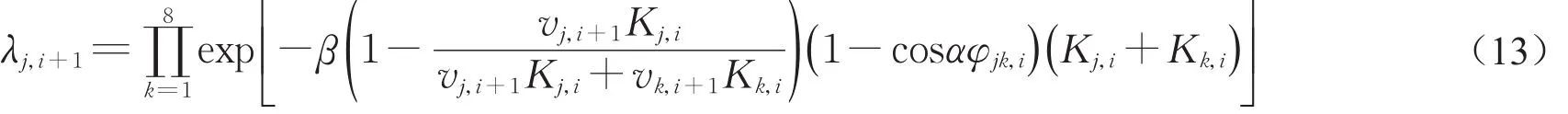
式中:j和k分别表示换乘平台内两个方向的客流,这两个方向可能相同;Kj,i、Kk,i分别为客流j和客流k在换乘平台内的密度(人·pm-2);φjk,i为客流j和客流k的冲突角度;α、β为待定系数,其中β>0。
(2)楼梯客流速度
根据文献[6],双向行人流分割楼梯空间后通常形成方向相反的两个“车道”(如图3所示),相反方向的乘客仅在“车道”交界处发生“摩擦”。根据观测,结点换乘设施楼梯段内的双向客流基本遵循上述规则,在形成车道后交界处的“摩擦”对于双向客流速度影响不大,因此,假定楼梯上双向行人流的冲突忽略不计。
以楼梯 A1 下行速度为例,当KA1,d,i<Kdc时,第i+1 时段的下行客流速度vA1,d,i+1=vd,f,当KA1,d,i≥Kdc时,有
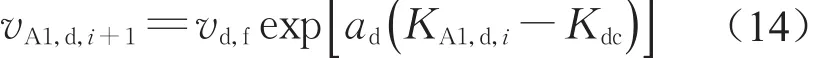
式中:vd,f为楼梯下行自由流速度(m·s-1);Kdc为楼梯下行客流速度是否为自由流速度的临界密度(人·m-2);ad为待定系数。
3.2 楼梯上下行客流宽度
首先到达楼梯的客流会以占据整个楼梯断面的形式通过,后到的客流则以靠右通行准则对楼梯空间重新分割[6],因此,当上下行客流均未到达楼梯或全部离开时,两股客流宽度均为0;当上下行客流中的一支尚未进入楼梯或全部离开楼梯时,另一支客流占据楼梯全部宽度;当楼梯上存在双向客流时,其渠化形成的“车道”数为2,上下行客流所占用车道如图3所示,以楼梯A1为例,存在以下4种情况:
(1)下行客流刚刚开始由梯前区域RA1通过断面A1-1,上行客流刚刚开始由换乘平台通过断面A1-2。第i+1时段下行客流宽度如式(15)所示。
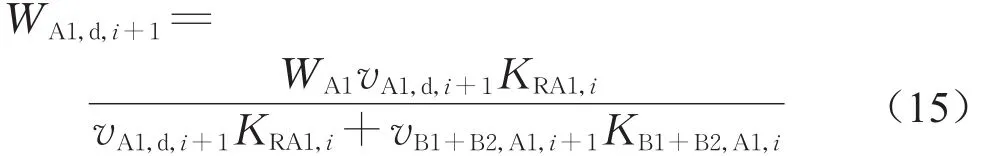
式中:WA1,d,i+1为第i+1时段楼梯A1下行客流宽度(m);WA1为楼梯A1宽度(m);vA1,d,i+1为第i+1时段楼梯A1下行客流速度(m·s-1);KRA1,i为第i时段末,梯前区域RA1的客流密度(人·m-2);vB1+B2,A1,i+1为第i+1时段客流B1-A1和客流B2-A1的平均速度(m·s-1);KB1+B2,A1,i为第i时段末客流B1-A1和客流B2-A1的平均密度(人·m-2)。
(2)楼梯A1内已经存在上行客流,而下行客流刚刚开始由梯前区域RA1通过断面A1-1。第i+1时段下行客流宽度如下:
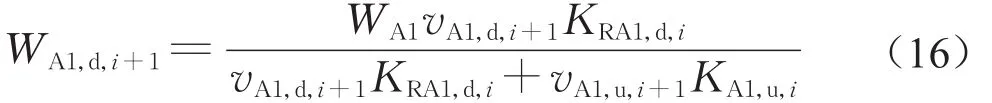
式中:vA1,u,i+1为第i+1 时段楼梯 A1 上行客流速度(m·s-1);KA1,u,i为第i时段末楼梯A1上行客流密度(人·m-2)。
(3)楼梯A1内已经存在下行客流,而上行客流刚刚开始由换乘平台通过断面A1-2。第i+1时段下行客流宽度如下:
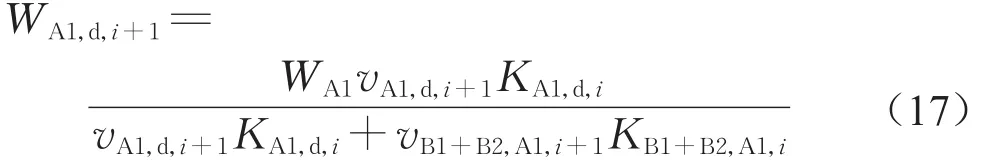
(4)楼梯A1内同时存在上行客流和下行客流。第i+1时段的上下行客流宽度维持第i时段的宽度不变。
3.3 楼梯客流占用长度
楼梯客流占用长度是上、下行客流在楼梯上实际占据范围的平面投影长度,用于计算楼梯客流密度。以楼梯A1下行客流为例,客流占用长度分别如图4所示。
3.3.1 楼梯无休息平台
楼梯无休息平台时客流占用长度对应于图4的4种情况如下:
(1)下行客流已经进入楼梯A1,但是尚未到达断面A1-2,有第i+1时段末楼梯A1下行客流长度其中,l为TJ梯级长度,φ为楼梯倾角。
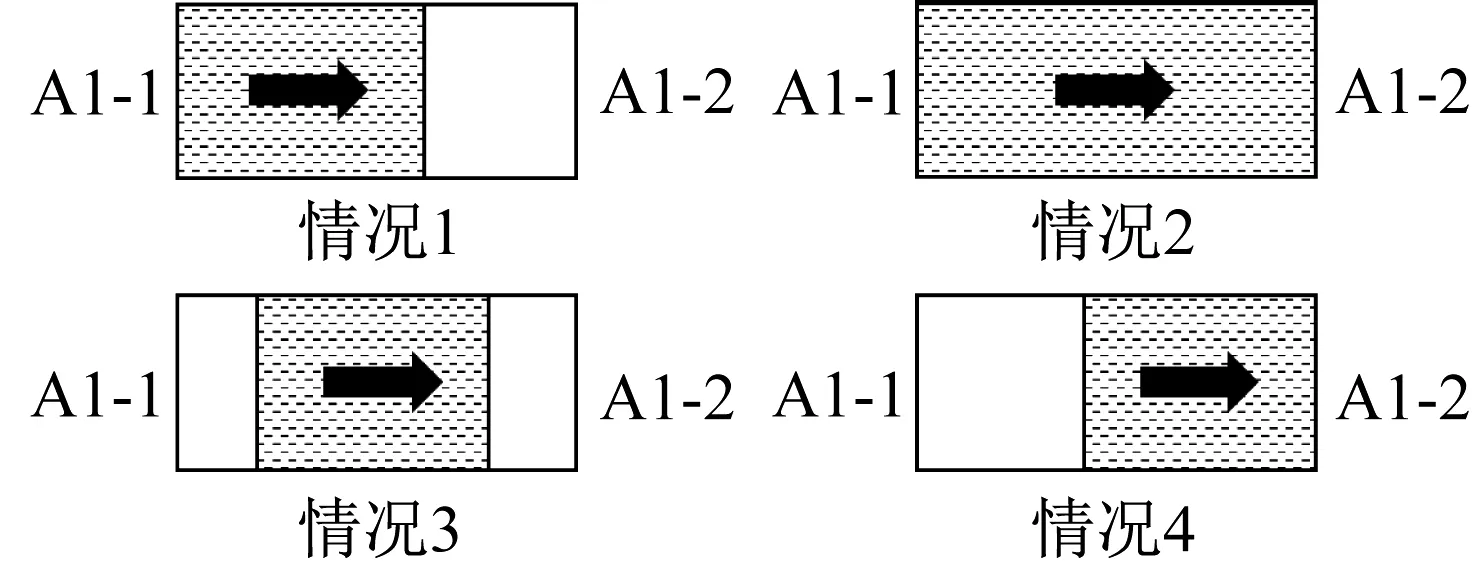
图4 楼梯客流占用长度Fig.4 Length of stairs passenger flow
(2)下行客流已经到达并开始通过断面A1-2,并且断面A1-1仍有客流持续进入楼梯A1,有LA1,d,i+1=LA1。
(3)下行客流不再持续进入楼梯A1,但是仍未开始通过断面A1-2,有LA1,d,i+1=LA1,d,i。
(4)下行客流不再持续进入楼梯A1,楼梯内的剩余客流通过断面A1-2陆续离开楼梯A1,有当楼梯内的剩余客流为0 时,LA1,d,i+1=0。
3.3.2 楼梯有休息平台
情况1时,若客流经过休息平台,则有LA1,d,i+1=LA1,d,i+vA1,d,i+1ΔT;若客流经过倾斜 梯段,则按照楼梯无休息平台情况计算。情况2、情况3和情况4仍按照楼梯无休息平台情况计算。
无论是否有休息平台,下行客流尚未到达断面A1-1或全部通过断面A1-2,则LA1,d,i+1=0。
4 算例
站台A和站台B的设施布置以及“十”形结点换乘设施布置如图5所示。
根据上海轨道交通某站结点换乘设施的调查结果,设定换乘平台沿站台A方向长4.5 m,沿站台B方向长5.9 m,即换乘平台面积为26.55 m2。楼梯A1和楼梯A2宽度均为2.8m,平面投影长度分别为10.2 m和9.9 m,其中休息平台长度分别为3.0m和2.7m。楼梯B1和楼梯B2宽度为3.1m,平面投影长度为4.5 m,无休息平台。各车门与楼梯的对应关系以及走行距离见表3。
客流速度参数取自文献[13-15],即①换乘平台客流:KPF,fc取0.43人·m-2、vPF,f取1.01 m·s-1、α、β和θ分别取1.271、0.072和0.062;②楼梯上行客流:Kuc取 0.71人·m-2、vu,f取0.69 m·s-1、au取-0.1932;③楼梯下行客流:Kdc取0.71人·m-2、ad取-0.2659、vd,f取0.90 m·s-1。站台客流速度取1.24 m·s-1[16],车门流量取2.09人·s-1[10]。左转比例取0.3,右转比例取0.7。KTQ,max取2.5人·m-2,Lq取2.5m。小时段长度ΔT为2s。
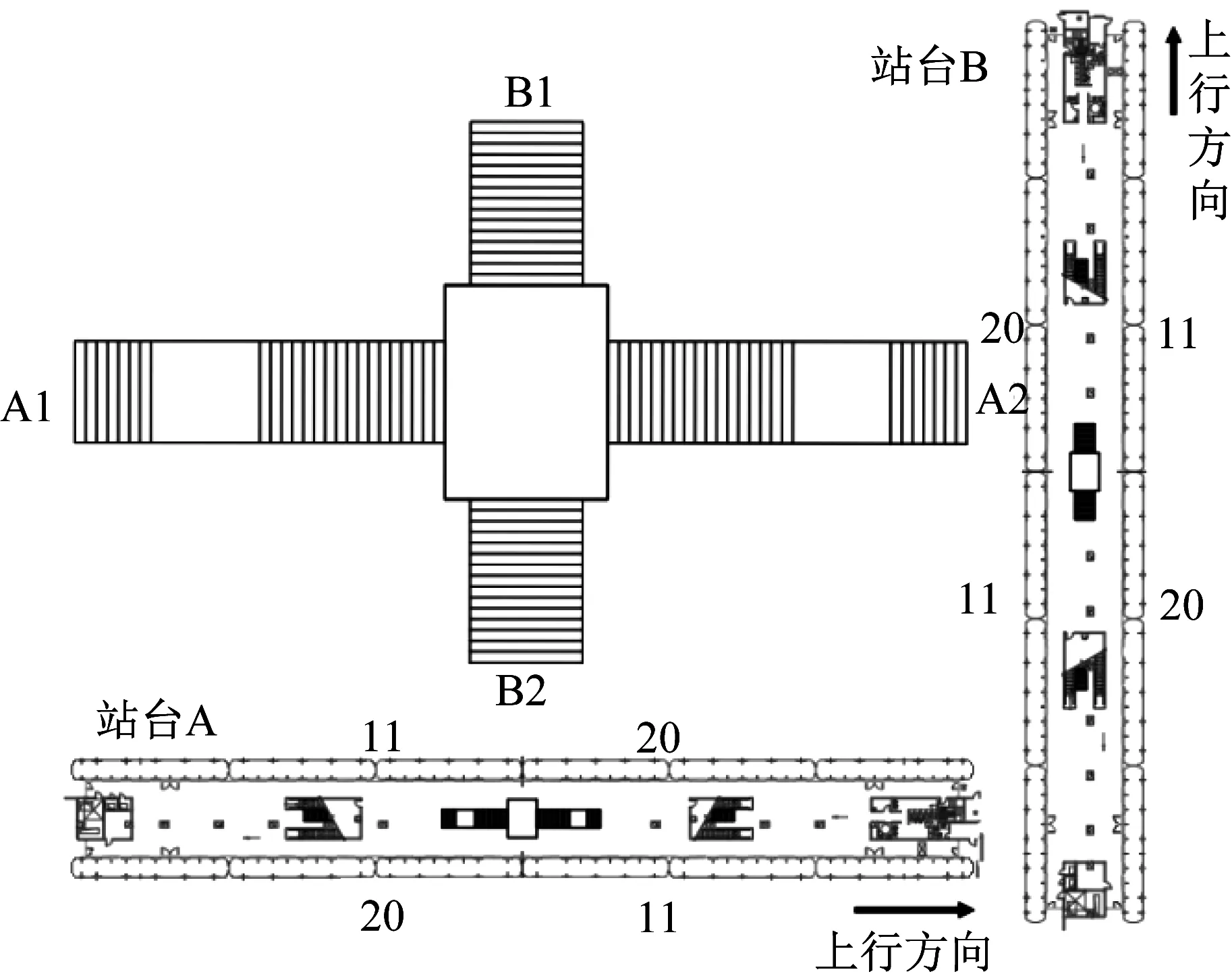
图5 站台设施布置Fig.5 Platform facility layout

表3 车门与楼梯对应关系及走行距离Tab.3 Correspondence and the distance between the door and the stairs
分析两线的上下行列车同时到达时,每个车门下车换乘客流人数分别为5人和6人时的设施拥堵情况,结果如下:①当车门下车换乘人数为5人时,设施清空时间为92s,换乘平台平均密度和最大密度分别为1.61人·m-2和2.71人·m-2;②当车门下车换乘人数为6人时,设施清空时间为104s,换乘平台平均密度和最大密度分别为1.87人·m-2和3.09人·m-2;③车门下车换乘人数为6人的情况相比车换乘人数为5人的情况,设施清空时间增加了12s,换乘平台的平均密度和最大密度分别增长16.1%和14.0%,拥堵情况较5人时严重。
5 结语
以城市轨道交通换乘站内的“十”形结点换乘设施为研究对象,以结点换乘设施的流密速关系为基础,考虑换乘平台内的多方向客流交织冲突,以及梯前区域、楼梯和换乘平台三者之间的客流状态相互影响关系,利用客流迭代建立了结点换乘设施行人拥堵分析方法。该方法可以通过不断调整输入条件,快速分析不同客流条件和设施方案条件组合下的设施拥堵情况。后续将在本文思路的指导下,实现其他类型结点换乘设施的拥堵分析,并通过不同客流组合的大量试算,尝试得到各类型结点换乘设施通过能力。

