基于灰色GM（1,1）模型的商品短期销量预测研究

刘雅琪，张 升，户一帆，靳立鹤

（河南师范大学，河南 新乡 453007）

对于商家来说，产品的采购、制作、营销都与销量紧密相关，备受商家重视。本文考虑到已知的相关样本数据量少，且销量的变化规律是一个不确定的因素，如果使用神经网络算法，将很难取得理想的效果。华中理工大学邓聚龙教授[1]在1982年率先提出了灰色系统的概念，并建立了灰色系统理论，该模型根据过去和现实的信息建模，推测将来的情况，提出事物发展变化的规律。它不受一般统计模型对原始数据种种要求的约束，具有实用性强、预测性能好的优点，能更准确地描述系统的状态和行为，适用于预测数据。目前已广泛应用于工业、农业等领域。本文利用基于灰色系统理论的GM（1，1）灰色模型来对问题进行预测[1]求解，并在此基础上开展综合性研究。

1 模型的建立

1.1 数据的检验与处理

为保证建模方法的可行性，需要对已知数列作必要的检验处理。设有效数为x(0)=[x(0)(1),x(0)(2), …,x(0)(n)]，计算数列的级比如果所有的级比λ(k)都落在了可容覆盖内，则数列x(0)可以作为模型GM（1，1）的数据进行灰色预测。否则就需要对数列x(0)做必要的变化处理，使其落入可容覆盖内。即取适当常数c，做平移变换：y(0)(k)=y(0)(k)+c,k=1,2,…,n，则使数列y(0)=[y(0)(1),(y(0)(2),…,(y(0)(n)]的级比为：

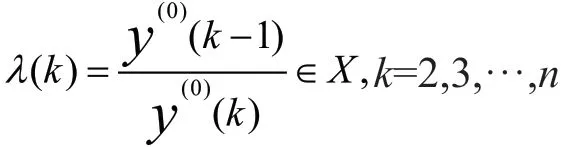
1.2 模型的建立

由表格知数列x(0)共有3个有效观察值：x(0)(1),x(0)(2),x(0)(3)，（分别是需预测月份在2016，2017，2018年的销量数据），对公式（2）进行累加生成，弱化随机序列的波动性和随机性，可得到新的数列：x(1)＝[x(1)(1),x(1)(2),x(1)(3)]，其中，然后生成x(1)的邻均值等权数列k=2,3,4，于是根据灰色理论对x(1)建立关于t的一阶一元微分方程用最小二乘法求解灰参数将灰参数代入，求解得最后，将上述结果累减还原，即可得到预测值：

1.3 模型精度检验

对所建立的GM（1，1）模型进行检验，判定模型是否合格。本文采用后验差比值（C值）和小误差概率（P值）来判断模型的精确度，将计算结果代入检验准则中求出相对残差检验：

对于以上模型，有以下两个检验准则：

当C＜C0时，称模型为均方差比合格模型。

当P＞P0时，称模型为小误差概率合格模型，精度检验的标准。

模型综合精度级别=MAX{p的级别，C的级别}。具体预测标准如表1所示。

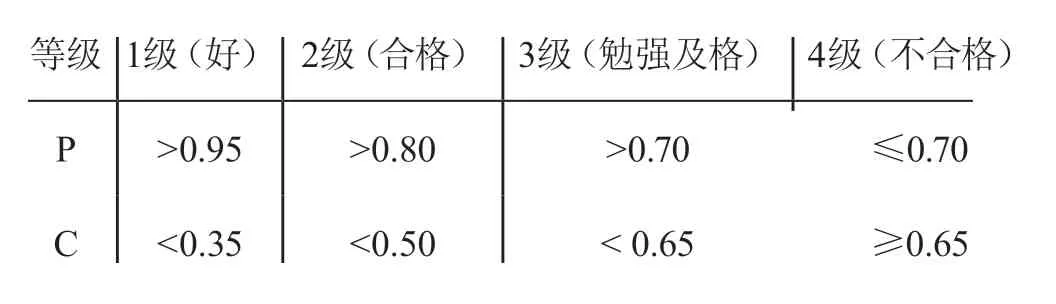
表1 精度检验等级参照

2 模型的求解

通过多次拟合后发现选取需预测月份对应的每一年的数据做原始数据比以2019年第一季度的数据作为原始数据或者直接以前连续n月的数据作为原始数据效果更好。现以预测地区以A250bc口味一商品5月份销量为例。

2.1 数据的检验与处理

设M=[44.163, 33.17, 44.241]，计算得到其级比数列为λ=(λ2,λ3)=（1.331 4, 0.749 8）。计算可容覆盖区间可看出所有的级比λ(k)都落在了可容覆盖区间内，所以，该建模方案是可行的[2]。

2.2 建立模型

给定原始数据序列：M=[44.163, 33.170, 44.241]，对原始数列M做累加得到数列N=[44.163, 77.333, 121.574]，接着，对N做紧邻均值生成，构造数据矩阵N和Y，利用公式：得出：

2.3 精度检验

通过后验差检验法将计算结果分别带入两个检验准则中，计算判断模型的精度是否达到要求，具体模型精度如表2所示。

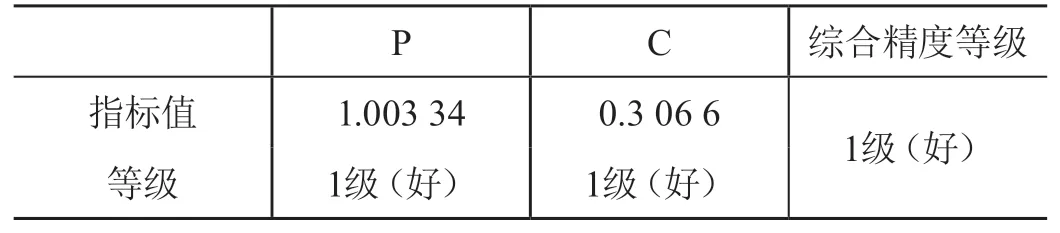
表2 模型精度检验

根据表2中精度检验结果可知，本团队所建立的模型中二模型精度等级为1级（好），精确度较高，可以进行预测。

2.4 模型预测与分析

文章选取产品2016—2018年销售数据，运用灰色预测GM（1，1）模型对2019年的销量进行预测，从检验结果来看，其通过了后验差检验，等级为一级，表明预测精度较高。产品短期内销量呈上升趋势，但是不同产品以及同一产品的不同口味之间销量差也很大[3]。因此，对产品采用不同的营销手段也很有必要。部分产品2019年第二季度预测销量如表3所示。

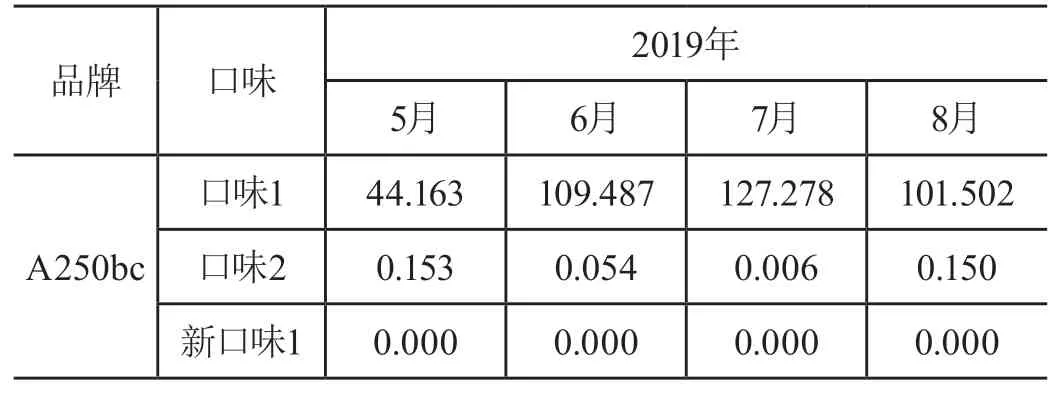
表3 部分产品2019年第二季度预测销量表

3 结语

本文采用灰色预测GM（1，1）模型对商品的销量进行短期预测，所得结果精确度较高，对帮助商家合理调整价格、有效解决库存等具有一定的参考意义。但是，由于数据较少，本文的预测精度有待提高。在未来的研究中，可以在获取更多数据的基础上，尝试采用不同的模型对其进行预测，以更好地帮助商家解决实际问题。