多维时频图像特征组合的电磁辐射源信号识别*

肖 祺，陈茂洋

（杭州电子科技大学 通信工程学院，浙江 杭州 310018）

0 引言

在电子对抗侦察领域，准确识别电磁辐射源信号的调制方式，可以为信号的下一步分析和操作提供有效依据，从而获得精确的情报数据。但在复杂电磁环境下，电磁辐射源信号调制方式多样化，对信号的分选和识别比较困难[1]。所以实现电磁辐射源信号的检测与识别准确化和智能化具有重要的意义。

针对调制方式多样化的电磁辐射源信号，要实现调制方式自动分类识别，就要提取信号特征。常见的特征提取方法主要有时域分析法、频域分析法、调制域分析法、谱相关法和时频域分析法等。这些方法都是对采样信号进行某种变换，使信号之间的特征存在明显不同，进而实现信号识别。文献[2]对BPSK、QPSK、MFSK 这3 类调制方式信号进行功率谱、平方谱特征提取并运用主成分分析对谱特征参数进行再提取，结合人工神经网络（Artificial Neural Network,ANN）进行调制识别。文献[3]提出了基于混合特征的支持向量机（Support Vector Machine,SVM）的识别方法，提取了5 种调制信号的瞬时特征和基于循环平稳和信息熵的特征。文献[4]采用信号的瞬时特征和高阶统计量特征，利用决策树进行调制识别。文献[5]提取了信号时频能量谱纹理特征，通过SVM 实现了6种调制方式的识别。文献[6]对8 种信号通过Choi-Williams 分布算法得到时频图像，使用卷积神经网络（Convolutional Neural Networks,CNN）对信号时频图像进行识别分类。目前，在信噪比较高的条件下，信号的调制方式识别方法较多。但是在低信噪比下，信号特征的鲁棒性较差，特征距离较小，许多方法的识别效果较差。本文提出一种时频图像角点和直线特征组合的调制方式识别方法，该方法在较低信噪比条件下，具有识别优势。

1 算法原理

假设接收到的信号表示为：

其中，t为信号时间，s(t)为源信号，n(t)为高斯白噪声。

本文利用不同调制方式的信号时频图像的差异特点，通过提取时频图像的角点和直线特征，实现电磁辐射源信号调制方式分类识别，其计算流程如图1 所示。

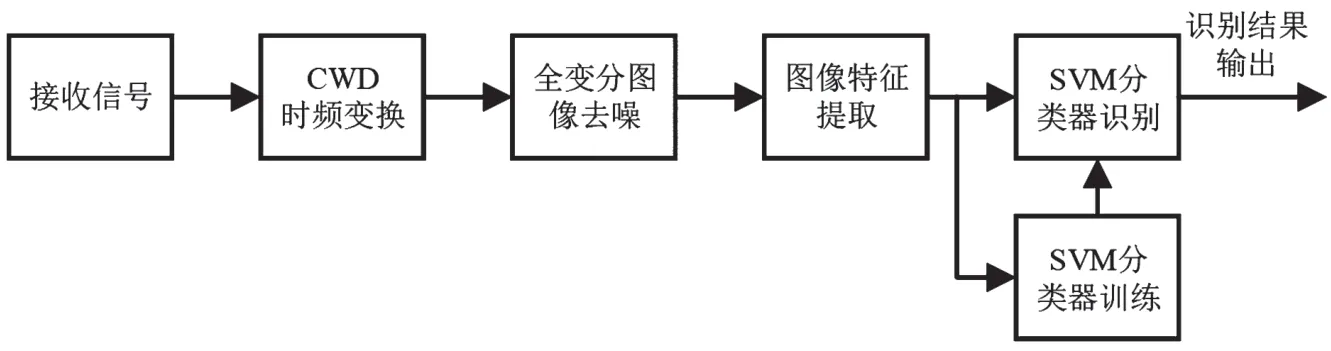
图1 计算流程

由图1 可知，获取信号时频图像后实现图像去噪，提取图像角点和直线特征组成多维特征向量，由SVM 分类器完成对特征向量的训练和识别分类。

1.1 时频变换

目前，获取信号时频图像的方法主要有短时傅里叶变换（short-time Fourier transform,STFT）、Wigner-Ville 分布（Wigner-Ville distribution,WVD）、平滑伪Wigner-Ville 分布（smoothed pseudo Wigner-Ville distribution,SPWVD） 和Choi-Williams 分 布（Choi-Williams distribution,CWD）。STFT 的 时 间和频率分辨率相互制约，时频分辨率低。WVD 具有理想的时频分辨率，但会产生交叉项，交叉项的存在会干扰真实信号的特征[7]。SPWVD 和CWD 都能有效抑制交叉项且具有良好的时频分辨率。

本文采用CWD 方法获取信号时频图像，其表达式为：

其中，σ为衰减系数，与交叉项的幅值成比例关系。

1.2 全变分图像去噪

在图像处理领域，全变分理论自提出以来，一直受到研究者的广泛关注，尤其是在该理论提出时所针对的图像修复和去噪领域。基于全变分模型的图像去噪可以在保护图像边缘信息的同时，降低图像噪声[8]。

设图像噪声模型为：

其中，u0(x,y)为含噪图像，u(x,y)为原始无噪图像，n(x,y)为高斯白噪声，像素点(x,y)∈Ω，Ω为图像定义域。

噪声使图像的灰度起伏变大，总变分也因此增大。原始无噪图像的总变分较小但又接近含噪图像，因此图像去噪问题可转化为总变分约束条件下相关性极小最优化模型，或者是相关性约束条件下总变分极小最优化模型。全变分模型可表述为：

上述优化模型的拉格朗日乘子法可表述为：

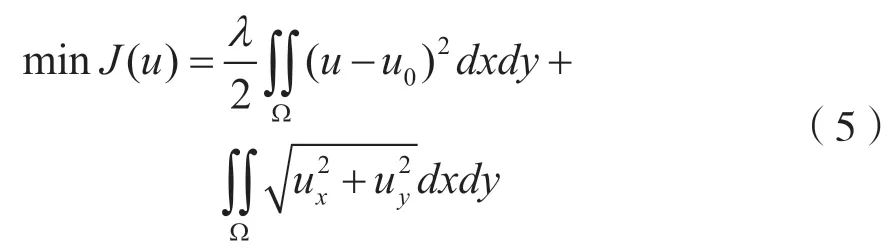
其中，λ起去噪与平滑作用，其大小与噪声水平有关。前一项为数据保真项，代表去噪图像和含噪图像之间的逼近程度，起保留原图像特征和降低图像失真度的作用。后一项为正则化项，能够很好地反映图像的边缘信息。由式（5）可导出相应的欧拉-拉格朗日方程为：

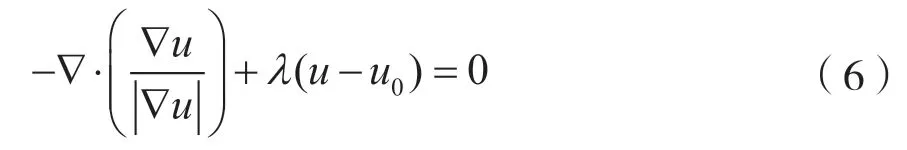
1.3 特征提取

通过Harris 角点检测算法得到时频图像中的角点位置，通过霍夫变换得到时频图像中的水平直线信息，从而得到以下特征：角点与直线的位置关系、角点的数量、水平直线段间的位置关系、水平直线段的数量、水平直线段的占比。其中角点与直线的位置关系包括角点全在直线上、角点不全在直线上和角点全不在直线上3 种，角点的数量则分为角点在直线上的数量和角点的总数量2 个特征值，水平直线段的位置关系包括在一条直线上、平行和多条平行3 种。

1.3.1 Harris 角点检测

角点可以反映出图像的重要特征，对图像的分析有极大作用。角点是一种信息含量很高的图像特征。

角点一般具有以下特点：

（1）该点附近区域的像素点无论在梯度方向上还是梯度幅值上都有较大的变化。

（2）该点的图像局部曲率突变。Harris 角点检测的基本思想是在图像上使用一个固定窗口[9]进行任意方向上的滑动，如果滑动前后窗口中的像素灰度变化较大，那么该窗口中就存在角点。

1.3.2 霍夫直线检测

霍夫变换（Hough Transform）于1962 年首次由Paul Hough 提出，于1972 年由Richard Duda 和Peter Hart 推广使用，是图像处理领域内从图像中检测几何形状的基本方法之一。可用霍夫变换来检测图像中的直线。

一条直线在极坐标系下可表示为：

图像中的每一条直线都与一对参数(r,θ)相对应，这个参数(r,θ)平面称为霍夫空间[10]。

霍夫直线检测的基本原理就是利用点与线的对偶性，即图像空间中的直线与霍夫空间中的点是一一对应的，霍夫空间中的直线与图像空间中的点也是一一对应的。因此霍夫直线检测算法就是把在图像空间中的直线检测问题转换到霍夫空间中对点的检测问题，通过在霍夫空间里寻找峰值来完成直线检测任务。

1.4 训练分类

使用支持向量机分类器对提取的特征向量进行识别分类。支持向量机结构简单，运算速度快，用小样本容量就能达到良好的识别分类效果。

SVM 的参数选取对于分类精度有很大的影响，惩罚参数决定了SVM 最优分类平面[11]对错误样本的容忍程度，核函数参数决定了样本间隔的尺度范围。为确定合适的惩罚参数c和核函数参数g，采用一种参数优化选取的方法。对于暂取定的c和g，把训练集作为原始数据集利用交叉验证方法（KCV）得到在此组c和g下训练集分类准确率，最终取使得分类准确率最高的那组c和g作为最佳参数。

径向基（radial basis function,RBF）核函数复杂度小且不受样本数量和特征维数的影响，因此本文选用RBF 核函数。

2 仿真实验与结果分析

本文使用二进制频移键控（2FSK）、四进制频移键控（4FSK）、最小频移键控（MSK）、二进制相移键控（BPSK）和正交相移键控（QPSK）这5种信号进行仿真。信号采样频率均为100 MHz。在信噪比为-6～14 dB 范围内，每种信号每隔2dB 产生600 个样本，合计3000 个样本，把其中2000 个作为训练集，剩下的1000 个作为测试集。具体的实验步骤如下：

（1）对信号进行Choi-Williams 时频变换，得到时频图像TF(t,f)。

（2）对TF(t,f)图像进行裁剪和全变分图像去噪，得到F(t,f)图像。

（3）对F(t,f)图像进行角点检测，设置阈值剔除伪角点，得到真实角点的信息数据。

（4）对F(t,f)图像进行二值化处理得到B(t,f)图像，对B(t,f)图像进行霍夫变换，得到水平直线的信息数据。

（5）通过角点和水平直线的信息数据得到所需要的6 维特征向量，利用SVM 对特征向量进行分类识别。

如图2 所示为在信噪比为0 dB 时，经过上述实验步骤得到的5 种信号的时频图像。表1 为图2所示的5 种信号的6 维特征向量，其中，角点与直线的关系由0 表示角点全不在直线上，1 表示角点全在直线上，2 表示角点不全在直线上；直线间的位置关系由0 表示平行，1 表示在一条直线上，2表示多条平行。由图2 和表1 可知，这5 种信号的角点和直线特征存在明显的区别，使用本文算法可以达到识别这5 种信号的目的。

表1 信号的6 维特征向量

图2 信号时频图

表2是在信噪比为0 dB时5种信号的识别结果。

表2 信噪比为0 dB 时5 种信号识别结果

由表2 可知，在信噪比为0 dB 时，5 种信号的平均识别率达到92.3%，对于2FSK、4FSK 和MSK这3 种信号，平均识别率达到97.2%，能较好地实现信号的识别分类。图3 是在不同信噪比下的信号识别率统计图。由图3 可知，信号的识别正确率随信噪比的升高而增大。

图3 不同信噪比下的识别正确率

实验最后验证了全变分去噪对识别性能的影响。由图4 可知，未经过全变分去噪的信号识别正确率明显变低。同时将本文算法与其他文献采用的算法进行比较。文献[3]提取了这5 种信号的瞬时特征和基于循环平稳和信息熵的特征，采用支持向量机进行识别。由图4 可知，在信噪比小于4 dB 时，本文算法的识别率远远大于文献[3]算法的识别率，本文算法的识别效果较好。当信噪比大于4 dB 时，两种算法的识别率都大于95%，但文献[3]算法的识别效果更好。以上结果可以说明，采用本文算法可以对这5 种信号有效识别，且可以运用在低信噪比环境下。

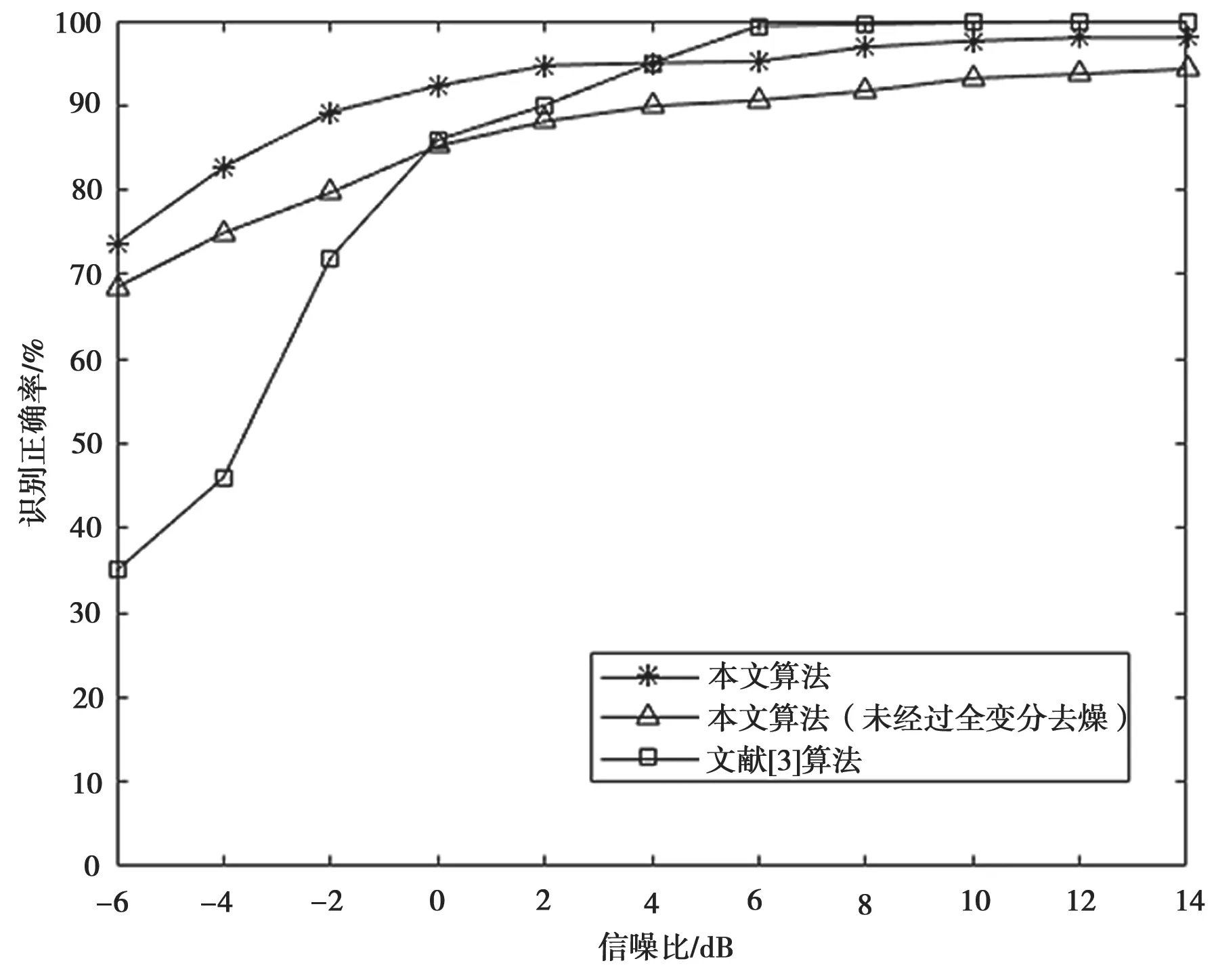
图4 识别效果对比情况

3 结语

本文利用Harris 角点检测和霍夫变换提取了信号时频图像的特征，将时频图像的角点和直线特征结合起来组成6 维特征向量，通过SVM 分类器实现了电磁辐射源信号的调制方式识别。实验结果表明，与其他算法相比较，本文算法在较低信噪比条件下识别效果较好，具有识别优势。