基于ABAQUS的黏胶织物传热性能模拟分析

张 洁, 刘新金, 张 娣, 谢春萍, 苏旭中

(1.江南大学 生态纺织教育部重点研究室,江苏 无锡 214122;2.无锡市金茂对外贸易有限公司,江苏 无锡 214122)

织物的舒适性在服用过程中十分重要,其中热舒适性是人体舒适的重要因素之一。利用有限元软件预测织物性能,可高质量低成本地完成织物产品的评估及优化[1]。关于织物的热传递性能,近些年,科研工作者青睐借助有限元方法对其进行仿真模拟,范坚等[2]建立织物二维传热模型及单元格控制方程,比较了不同结构的织物一维及二维传热情况;陈扬等[3]通过织物平板简化模型探究不同因素下模型内部及织物外表面的温度情况。张鹤誉等[4]基于有限元方法针对玻璃纤维织物的传热性能进行了模拟分析,采用实验对模拟结果进行了验证。朱方龙[5]对附加PCM相变材料层的热防护服装进行了数值分析,验证了PCM织物层的防护作用。Barauskas Rimantas等[6]利用有限元模型对生物陶瓷添加剂增强织物的耐热性进行了研究。

本文通过代数插值方法求纱线弯曲中心线,进而在建模软件中采用扫掠横截面等建立织物模型;基于有限元软件ABAQUS分析含有空气参与的织物结构系统,再利用实验就仿真模拟分析方法的有效性与可行性进行验证;并基于此对织物传热性的影响因素进行分析,以更好地研究热防护高性能材质的织物。

1 理论与计算

1.1 传热基本理论

热量是通过纤维及空气间的交换在织物内传递,由于沿厚度方向热量交换较多,因此可将织物传热简化成沿着“人体—织物—外部环境”的一维传热。热量的传递方式有三种:热传导、热对流及热辐射。由于热量交换过程中温度的变化较小,因此热辐射带来的影响可忽略不计。热分析遵循能量守恒定律,即对于一个没有质量流入或流出的封闭系统而言,热量等于系统做的功与系统内能、系统势能、系统动能的总和。根据傅里叶定律,在单位时间下,单位面积热传导的导热热量与板面积及温度变化率同比例增长,导热系数数值的大小直接反应材料的导热能力,通常由实验测定。热流密度是在单位面积下垂直于等温面的方向上的传热效率,由傅里叶定律可求得[7]:

(1)

由于热传导遵循傅里叶定律,所以通过傅里叶定律进一步计算织物的热阻,可由下式得到:

(2)

式中:q为热流密度,W/℃;ΔT为被测织物两面的温度差,℃,R为热阻,m2·K/W。

热对流是指固体表面与接触的流体之间由于存在温差而引起的热量交换,可用牛顿方程来描述:

q=h(Ts-Tb)

(3)

式中:q为热流密度,W/℃;h为对流换热系数,W/(m2·K);Ts为固体表面温度,℃;Tb为流体温度,℃。

1.2 纱线导热系数的计算

纱线是多孔性物体,纤维内部和纤维之间有很多孔隙,孔隙中也充满空气,因此纱线自身的有效导热系数应由纱线中纤维的导热系数及空气的含量两个因素决定。纱线中纤维的体积分数及纱线的导热系数可由下式算出[8]:

(4)

Ky=KfVfy+Kair(1-Vfy)

(5)

式中:Tt为纱线的线密度,tex;ly为纱线的长度;Vy为纱线的体积;ρf为纤维的密度;Vyf为纤维在纱线中的体积分数。Ky为纱线导热系数;Kf为纤维导热系数;Kair为空气的导热系数。

1.3 织物模型的建立

织物模型建立一般是通过定义纱线横截面和纱线在织物中的成纱轨迹来实现。纱线的理论轨迹主要有三种:正弦(余弦)曲线法、折线法和分段拟合法。确定纱线中心线要遵循以下原则:既要保证纱线接触充分,又要防止出现纱线接触过盈[9]。但采用以上方法建立的模型织物交织点位置的纱线接触以及浮长线的弯曲都不够理想,本文受到Perice圆形截面纱线理论的启示,通过选取织物的几个特殊节点,并基于数值分析方法中的牛顿插值对纱线中心线的方程曲线进行拟合。下面是平纹织物纱线的拟合过程[10]:

现设经、纬纱的长袖和短袖分别用a1、b1和a2、b2表示,纱线间的间距和屈曲波高分别用lj、lw和hj、hw表示。如图1所示,分别以织物经、纬纱及厚度方向表示X、Y和Z建议直角坐标系。再根据几何关系建立织物厚度方程Z=f(y),y∈[-lj,lj]。

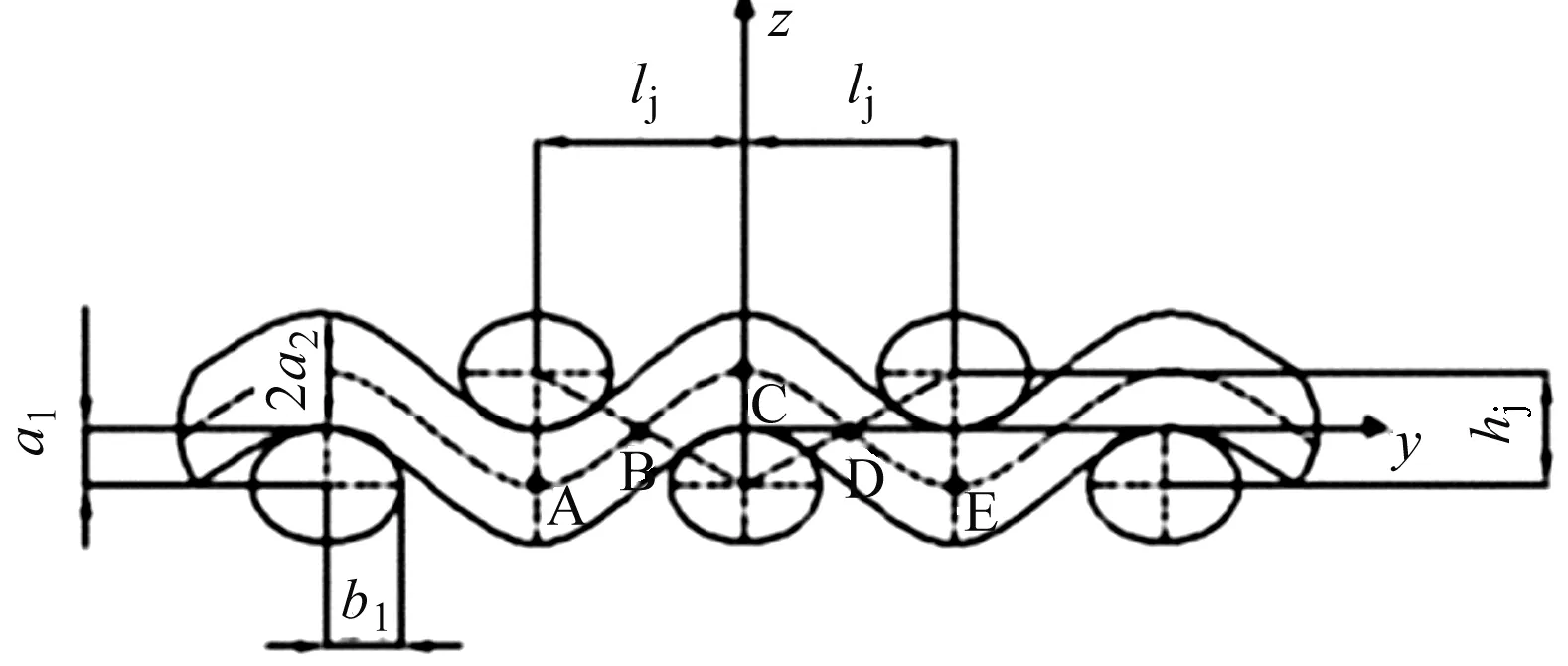
图1 织物横截面模型Fig.1 Fabric cross-sectional model

图1的曲线方程是关于Z对称的,且不难得出几个特殊节点A、B、C、D、E的坐标,再利用数值分析牛顿插值公式中的K阶均差公式。

(6)

可得到各特征点的四阶均差值,根据四次多项式可得纱线曲线方程:

(7)

2 有限元分析

2.1 模型构建

本文选用平纹组织黏胶织物为研究对象。经纬纱线密度为14.8 tex,织物经纬密度为420×350/10 cm、织物总紧度为80%。参照ISO 5084—1996《纺织品及纺织制品厚度的测定》使用YG 141LA型厚度仪(宁波纺织仪器厂)多次测量织物厚度,织物厚度为0.27 mm。

近年来,纱线截面轮廓理论主要分为圆形、椭圆形、跑道形和凸透镜形等。利用VHX-5000超景深显微镜(基恩士有限公司)对织物样品的截面模型进行观测,可以发现织物截面中纱线之间互相挤压缠绕,导致纱线截面改变,交织点处纱线截面变形严重,对于大多数纱线的截面,纱线与纱线间在保证接触不过盈的情况下可以充分接触,则本文可大致将织物纱线视为椭圆形。在超景深显微镜中通过显微图像技术测量以多次测量取平均值的方式对织物纱线的几何参数进行测量,结果如表1所示。

表1 织物截面几何参数Tab.1 Geometrical parameters of fabric cross section mm

根据纱线曲线方程(7),在Auto CAD建模软件中,将方程得到的节点利用B样条曲线光滑的连接实现纱线中心线,再利用扫掠和平移的方法对织物进行物理建模,如图2所示。利用布尔运算建立空气模型,并将其与织物模型装配一体,如图3所示。其中,较亮面为整体模型的侧面,较暗面为系统模型中与外界空气产生对流作用的面。

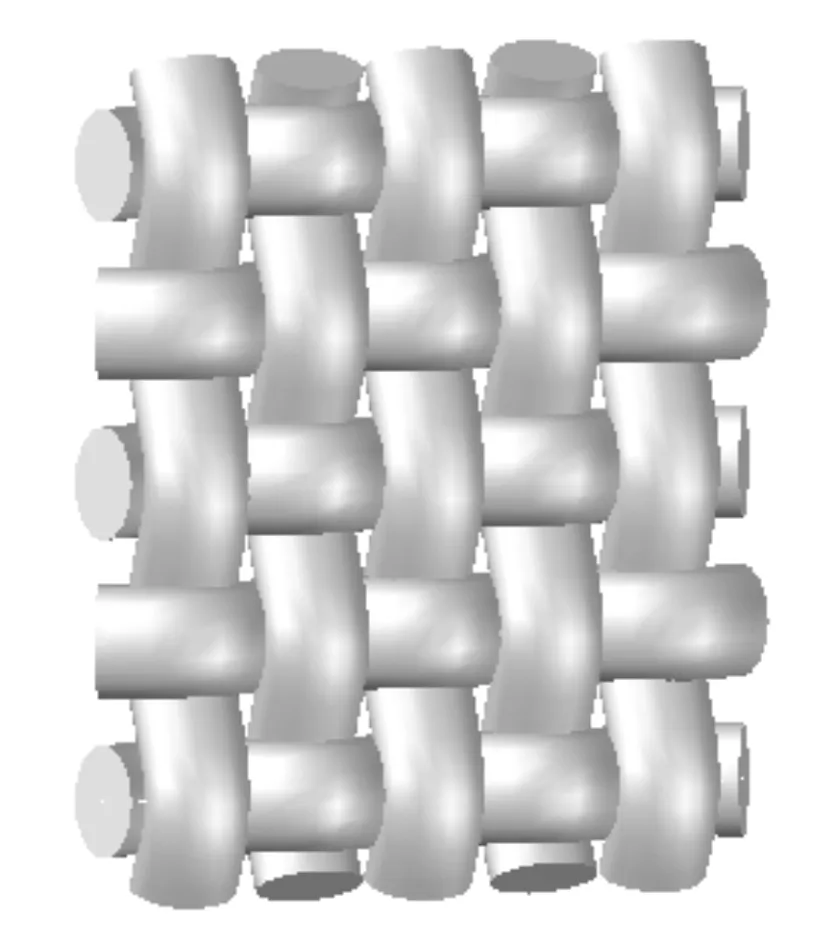
图2 织物模型Fig.2 Fabric model

图3 空气模型Fig.3 Air model

2.2 ABAQUS有限元模拟

ABAQUS是用于工程模拟的有限元软件,可解决一系列简单或相对复杂的线性与非线性工程问题。在模拟织物传热性能前,为更好地创建织物传热环境,本次分析计算阶段选用ABAQUS/Standard求解方式,便于分析和计算,现考虑:1)忽略衡量织物材料导热性能的导热系数及比热容数值随温度的变化;2)假设织物侧面边界绝热,仅考虑织物上下表面与外界空气的热交换;3)织物表面的流体即空气与织物表面无滑移,是不可压缩、稳态的流体[11-12]。材料属性如表2所示。

表2 材料属性Tab.2 Material properties

将Auto CAD中的模型以sat格式导入有限元软件ABAQUS中,定义材料性质。假定模拟环境为人体舒适的室温,设置模型初始温度为t0=24.5 ℃。建立热传递稳态分析步,定义边界条件,定义相互作用,单元类型选用standard四节点线性传热四面体(DC3D4)对模型进行网格划分,适用于分析模型的热传递。设置热学场输出变量和历史输出变量,其他接受默认值,提交作业并运算。其中边界条件的设定为第一类边界条件[12],织物内侧贴近人体皮肤,定义织物内侧温度为ti=36 ℃。则边界条件控制方程如下:

k2t2+k3t3+k4t4-(k1+k2+k3+k4)t=-t1ti

(8)

k1t1+k3t3+k4t4-(k1+k2+k3+k4)t=-t2t0

(9)

式中:t为任意某单元格的温度,t1、t2、t3、t4为此单元格上下左右单元格的温度,k1、k2、k3、k4为此单元格上下左右单元格的导热系数。

由于两边边界处为绝热,则两边边界处的控制方程为:

k1t1+k2t2+k4t4-(k1+k2+k4)t=0

(10)

k1t1+k2t2+k3t3-(k1+k2+k3)t=0

(11)

2.3 ABAQUS有限元模拟结果

ABAQUS运算结束后,在Visualization模块可查看传热状态时及传热平衡时织物温度和热流量分布云图(图4)。在模型中提取三个节点,导出节点温度随时间变化的曲线,如图5所示。节点A为空气层与织物内表面相交面的温度分布,节点B为织物横截面内温度分布,节点C为织物与人体间空气层横截面内温度分布。

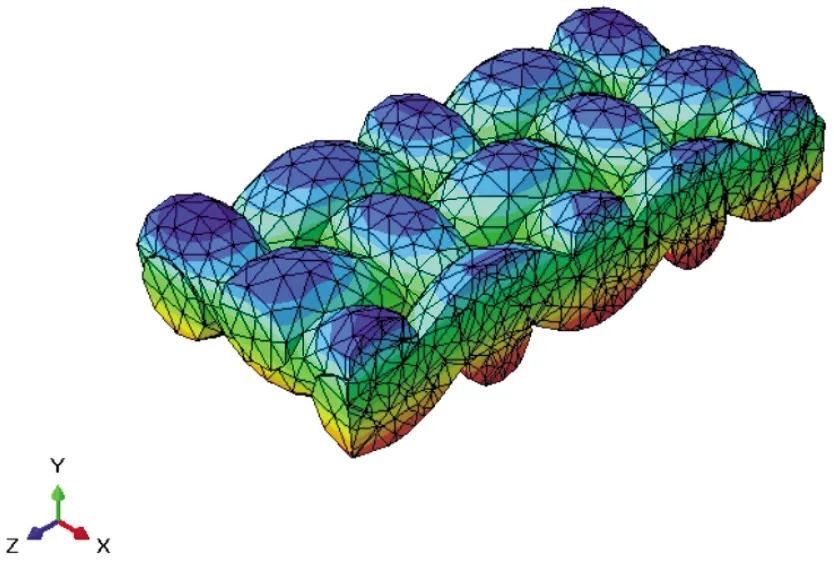
图4 织物截面的温度场云图Fig.4 Cloud diagram of temperature field of fabric cross section

图5 织物节点温度变化Fig.5 Node temperature change of fabric

对于ABAQUS模拟分析结果,可通过report导出节点温度和热流量,结合式(1)(2)对结果进行计算,可得到ABAQUS分析的织物模拟热阻为0.011 4 m2·℃/W,克罗值与热阻的换算关系为:1 clo=0.155 m2·℃/W,则模拟结果的织物克罗值为0.073 5 clo。织物参照GB/T 11048—1989《纺织品 保温性能测试标准》,为得到织物传热的保温率、传热系数和克罗值等参数,现利用平板式织物保温仪对其进行测量。将ABAQUS仿真模拟得到的克罗值结果与实验对比,其中误差值/%=(模拟结果/实验结果-1)×100,可得误差为8.12%。

为了再次验证模拟结果,在恒温恒湿实验室中将织物平铺在36℃的恒温加热板上,利用UT300A红外测温仪(优利德科技有限公司)对织物外表面选取的目标节点进行表面温度测量,在温度达到平衡前,以取平均值的方式记录温度变化,并将其结果与ABAQUS软件模拟分析的进行对比,如图6所示。

图6 织物外表面平均温度变化Fig.6 The average temperature variation of the outer surface of the fabric

由图4及图5可得出,热量会透过织物由其内侧向外侧进行传递,即在沿着其厚度方向,热量和温度慢慢变小。根据不同节点的温度变化,可得在40 s内织物外表面的温度上升迅速,而后上升缓慢且逐渐趋于平缓。由图6可得,织物外表面温度变化的模拟结果与实验结果相近,利用决定系数公式计算两条曲线的拟合度,可得决定系数为0.957 2,以上都可以说明模拟结果与实验结果的误差较小,进一步证明了上述有限元分析方法的可行性及模型建立的有效性。模拟结果与实验结果有所差异,分析认为是纱线存在毛羽或松散现象,导致实际情况纤维在纱线中的比例与实际情况存在误差,模型情况下空气的占比大于实际情况中空气的占比,进而造成温度上升的差异;其次,模型侧面与外界的热交换及热辐射带来的热量损失也对结果有一定的影响。

3 不同因素对传热性能的影响分析

3.1 空气层厚度对传热性能的影响

衣物在穿着过程中并非紧贴皮肤,而是在织物和皮肤间或织物与织物之间存在一定的空气层,由于空气的导热系数与纤维本身的导热系数相差甚远,因此空气层的存在会对织物的传热过程产生影响。研究空气层厚度如何影响织物传热性能,在上述模型的基础上,考虑几种不同空气层厚度的织物模型,织物厚度为0.28 mm,将空气层以0.1 mm为梯度增加,直至空气层厚度为0.5 mm,如图7所示。

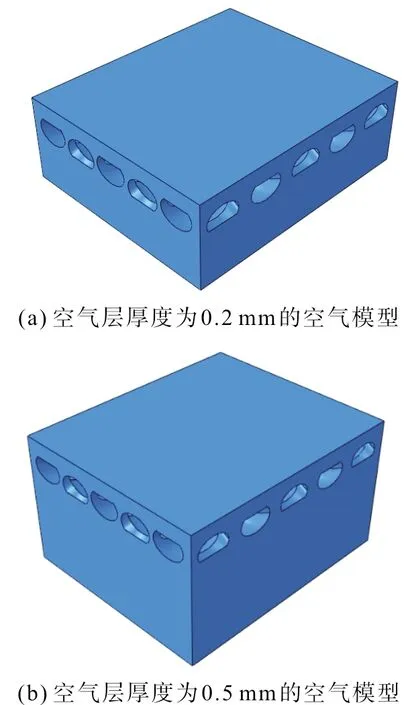
图7 空气模型Fig.7 Air model

赋予纱线及空气属性,设定边界条件及相互作用,仿真计算,并对数值模拟的结果进行分析,模拟结果见图8所示;不同空气层厚度时,织物外表面温度随时间变化的曲线如图9所示。图10为温度差与空气层厚度的关系。

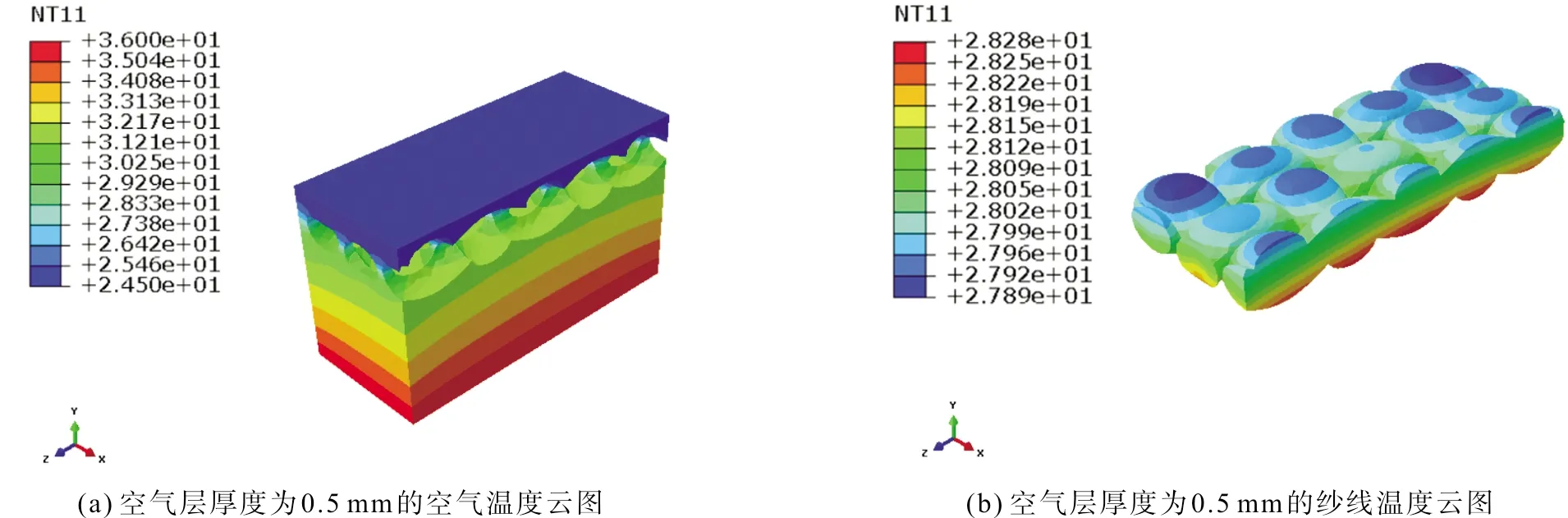
图8 模型温度场分布Fig.8 Cloud diagram of temperature field distribution

分析模型温度场分布云图及曲线可得,当热量通过空气层传递到织物时,织物外表面温度表征了传热情况。织物外表面温度越高,皮肤透过空气层传递到织物的热量越多。织物外表面温度随着时间逐渐升高,最终趋于缓慢,达到热平衡状态(图9)。随着织物与人体皮肤间的空气层厚度的增加,织物外表面温度逐渐降低,传递的热量越来越少,且下降的梯度越来越小(图10)。这是因为由于此次模拟中假设空气层是静止均匀空气,静止空气的导热系数较小,是优良的保暖介质,织物与皮肤间的空气含量越多,阻挡的热量就越多,空气含量增大到一定程度后,热量的传递速度减缓,下降的梯度减少。

图9 不同空气层厚度的织物表面温度变化Fig.9 The temperature variation of fabric surface with different air tightness

图10 温度差与空气层厚度的关系Fig.10 Relationship between temperature difference and air thickness

3.2 织物厚度对传热性能的影响

为探究织物厚度对织物传热性能的影响,选取了10种常见线密度纱线来进行实验模拟。线密度反映了纱线的粗细程度,改变纱线线密度进而可改变织物厚度。为保证单一变量,设计织物组织皆为平纹织物,织物经纬向密度相同,运用上述建模方法建立织物模型,织物几何结构参数如表3所示。其他前处理同上述过程,提交作业进行运算,模拟结果见图11。

表3 织物几何结构参数Tab.3 Geometrical parameters of fabric

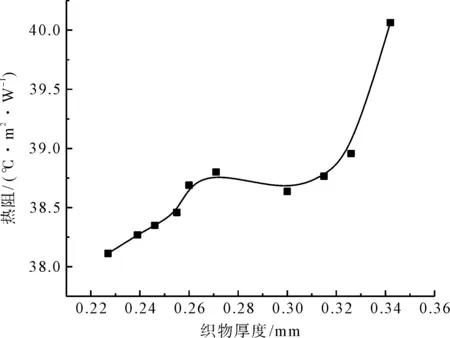
图11 不同织物厚度的热阻变化Fig.11 Change curve of thermal resistance with different fabric tightness

根据模拟过程及结果可得,随着线密度的减少,织物厚度逐渐减小,因此织物传递热量逐渐增多,克罗值逐渐减小。这是因为在经纬密和组织相同的情况下,使用线密度较大即较粗的纱线织造的织物单位面积内纱线交织得更加紧密,经纬纱之间接触面积增大,纱线间束缚的静止空气减少,但由于织物更加紧密,束缚的空气更加稳定,且织物厚度的增大导致传热通道变长,热量在纱线之间进行连续性传导,织物的热阻逐渐增加。且根据傅里叶定律,热流密度是指在与传输方向相同的单位面积上的传热速率,厚度增加时,热量在传输方向单位时间的传热效率就会减慢,热量传递较少,织物热阻增加。

4 结 论

本文基于常见平纹机织物纱线交织情况,引入数学数值分析中的牛顿插值方法对纱线中心线方程进行拟合,再利用绘图软件对其进行三维建模,导入有限元软件中模拟织物在服用状态下的传热情况,分析织物的热舒适性。后采用实验方法验证了有限元方法模拟结果及模型建立的有效性,继而基于上述方法模拟预测了不同空气层及不同织物厚度情况下的织物的热传递性能。研究得出:随着织物与皮肤间的空气层厚度的增加,织物传递的热量越来越少,且传递速度逐渐降低,下降梯度逐渐减小;纱线线密度越大即织物厚度越大的织物,织物的热阻越大,传递的热量越少。

PDF下载