基于空间量证明的共识算法综述

王昱博 马春光

摘   要：在区块链系统中，空间量证明被认为是比工作量证明更绿色、更经济的选择。与工作量证明不同，空间量证明将存储作为投入的资源，以此有效地避免資源的集中化，提高不同矿工之间挖矿的公平性。文章将空间量证明作为主要论述对象，列举了区块链中现有的物理资源消耗型证明技术，对其中以存储量作为消耗资源的证明技术进行展开，阐述了空间量证明的当前研究现状，对将基于空间量证明的共识算法与区块链结合的难点进行分析并总结现有的解决方法。

关键词：区块链;空间量证明;共识算法

中图分类号： TP301.6          文献标识码：A

Abstract： In the blockchain system， proof of space is considered a greener and more economical choice than proof of work. Different from proof of work， the proof of space takes the storage as the consuming resource， so as to effectively avoid the concentration of resources and improve the fairness of mining among different miners. Summary takes proof of space as the main object， listing the existing proof technology of physical resource consumption in blockchain， detailedly discussing the proof technologies which take storage as consuming resource， generalizing current research status of proof of space， analyzing the difficulty of applying the consensus algorithm based on proof of space in blockchain and summarizing the current solution.

Key words： blockchain; proof of space; consensus algorithm

1 引言

比特币[1]作为第一个以区块链技术实现的应用，一经问世就吸引了众多研究人员的目光，这一现象也使得区块链相关的技术得到了飞速发展。尽管最初区块链的应用仅限于电子货币[2]，但随着研究人员的不断尝试与创新，区块链技术已经开始逐渐融入各行各业，如医疗[3]、智能家居[4]、卫星通信[5]等。共识算法作为区块链的核心技术之一，其保证了区块链系统的分布式一致性，对推动区块链的发展有着重大作用，也自然而然的被广大研究人员所关注。

区块链是通过采用对等（Peer-to-Peer，P2P）网络组织所有节点[6]，并采用激励机制使得每个节点自愿参与系统维护的过程，而共识算法就是为了实现在这样一个分布式系统中保证不同节点数据存储的一致性。但因为P2P网络中节点间无法相互约束，且激励机制使得区块链系统中有利可图，这必然会出现一些节点希望通过不诚实行为，获得比诚实节点更高的利益。为了防止潜在的不诚实行为的出现，系统必须通过恰当的共识算法使得不诚实的行为被大多数用户所认可。

对于可自由进入的公链系统而言，缺乏身份验证是一个主要的问题。敌手可能通过制造出许多虚假身份使得自己成为系统中的“大多数”，从而危及系统的安全性，这种攻击被称为“女巫攻击（Witch Attack）”。共识算法要求每个参与的节点必须消耗一定资源来生成证明，从而证明自己的身份，由于每个节点拥有的资源有限，故能生成的证明也是有限的，通过这种方式来提高伪造身份（即，生成证明的过程）所需要的代价，从而一定程度上可以抵抗“女巫攻击”。

投入资源一般分为物理资源和虚拟资源，其中虚拟资源是指现实不存在，而仅存在于区块链系统中的资源，例如权益证明（Proof of Stake，PoStake）[8]中的币龄（Coin Age）（即币持有的天数X币的数量）、授权股份证明[9]（Delegated Proof of Stake，DPoStake）中的股权（与持有资产的数量呈线性关系）等。而物理资源主要是指硬件资源，例如计算受限（Computation bound）工作量证明（Proof of work，PoW）中的计算能力、内存依赖（Memory dependency）PoW的内存相关资源。而内存依赖型函数一般是被分为两类—内存受限函数（Memory Bound Functions，MBF）和内存难解函数（Memory Hard Functions，MHF），其中MBF依赖于访存时间，而MHF依赖于内存的消耗。空间量证明（Proof of Space，PoSpace）使用的磁盘空间也属于物理资源的一种，本文对四种物理资源进行介绍。

计算受限的PoW：计算受限算法是通过一段时间内CPU计算操作有限来抵抗女巫攻击。这种方法最早由Dwork和Naor[10]提出，用于阻止垃圾邮件泛滥。在发送电子邮件之前，验证者必须执行一些计算工作并生成一个可以有效验证的证明，以使得发送大量垃圾邮件需要付出一些时间上的代价，使得任何人不能无节制的发送垃圾邮件。

内存受限的PoW：基于平衡设备差异和坚持本地计算这两个要求，Abadi等人[11]和Dwork等人[12，13]相继提出了内存受限函数。内存受限函数主要是通过访存时间来决定的，其复杂性度量是内存访问的次数，而不考虑实际使用的内存容量。内存受限的PoW的特点在于，它需要不断地通过访存和少量计算对内存进行填充，此时访存时间成为了影响挖矿速度最主要的因素。因此，为了消除系统中高速缓冲存储器（Cache）对访存时间的优化，必须强制对内存填充的数据块至少大于Cache的容量。

内存难解的PoW：内存难解函数的主要思想是，对于给定的操作次数，设备需要尽可能多地消耗内存。Percival[14]给出了内存难解函数的概念并设计了满足条件的Scrypt算法。由于Scrypt算法对内存有一定的需求，故可以一定程度上抵抗ASIC带来的不公平性，但现场可编程门阵列（Field Programmable Gate Array，FPGA）仍旧可以在以Scrypt算法为基础的挖矿活动获得很大的优势。

PoSpace：PoSpace[15，16]是以磁盘容量作为投入资源来获取记账权的资源消耗性证明。与基于MHF的PoW类似，PoSpace也需要投入大量的存储空间来解决某个问题[18]。不同的是，PoSpace需要先在本地生成一个很大的随机文件，然后读出每次随机挑战所对应的数据作为空间量证明，以证明自己确实投入了与随机文件相同大小的空间量。此外，MHF运算一次只需要几分钟且用完之后就会丢弃，而PoSpace生成随机文件往往需要几个小时，且生成的随机文件需要长期保存。

比特币是通过工作量证明来抵抗“女巫攻击”，传统基于哈希的PoW有一些缺點，最明显的是不能有效地防止使用专用集成电路（Application Specific Integrated Circuit ，ASIC）。ASIC的哈希集成单元常常会使得在CPU上提供100倍加速的同时导致10000倍能源消耗，这使得装备了ASIC的对手相对于使用普通设备的用户具有巨大的优势，但与此同时也带来了巨大的能源损耗问题[7]。空间量证明一直以来被视为是工作量证明的一种替代方案。由于PoSpace是以磁盘空间作为投入资源，这使得个人很难将大量的资源集中化，这将很好的解决专用设备所带来的能源浪费和不公平性问题。

本文以空间量证明技术为核心，从不同的方面讨论空间量证明相关研究及其发展。文章结构安排为：首先，讨论包含空间量证明技术在内的存储证明技术，罗列各类存储技术发展中的重要成果，并展示这些成果对空间量证明技术的发展的促进作用;然后，对现有的空间量证明技术类型划分，并阐述其安全性的发展;接着，分析将空间量证明技术与区块链结合存在的难点，并总结现有的解决方案。最后对空间量证明技术的发展和研究趋势进行总结。

2 存储证明技术

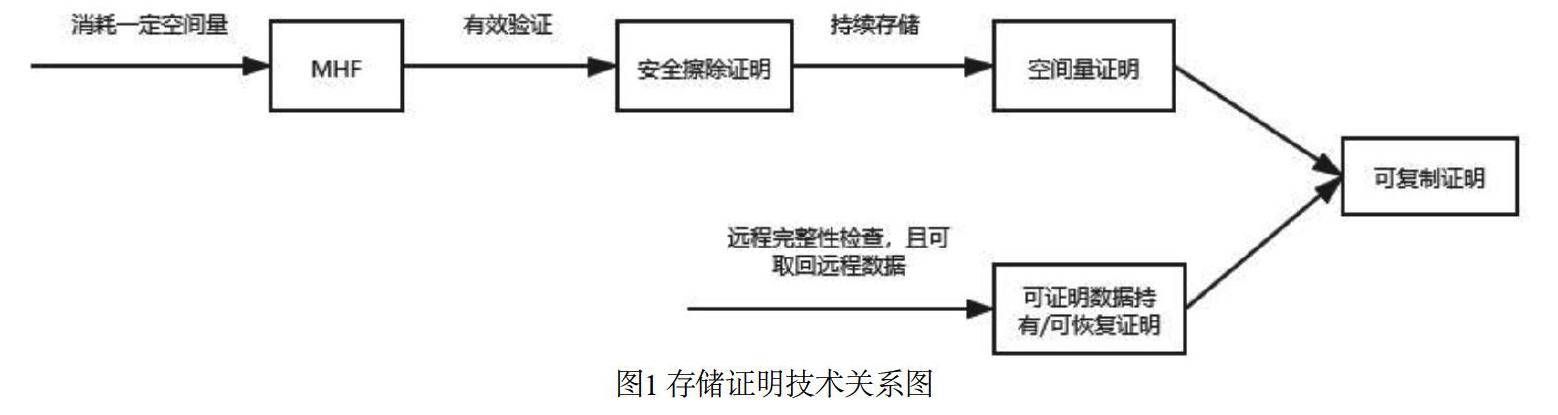
空间量证明技术作为一种存储证明技术，其发展与其他存储证明技术之间有着密不可分的联系。从这些技术中可以看到空间量证明技术的发展过程，以及未来的发展趋势。本节致力于对安全擦除证明、可证明数据持有、可恢复证明、空间量证明和复制证明进行区分，将对一些基本成果进行论述。其各种技术之间的关系如图1所示。

2.1安全擦除证明

对于某一个存储量有限的设备，如果怀疑设备中可能存在恶意程序或希望删除设备中的机密文件，研究人员可以通过安全擦除证明（Proof of Secure Erasure，PoSE）来实现。

PoSE是由验证者V和证明者P参与的双方协议，协议过程分为两个阶段：第一阶段，V向P发送一个与P存储器容量相等的随机文件;第二阶段，P保存V的随机文件，并对文件进行适当计算，将结果返回给V，以证明自己确实保存了完整的随机文件。

2010年，Perito等人[19]为了实现设备认证和代码更新首次引入了PoSE的概念。Perito等人希望通过哈希函数对随机文件进行处理，并要求使用随机文件的最后k位作为密钥。由于P在随机文件的最后才能获得密钥并对随机文件进行处理，这使得在随机文件传送完成之前，P需要前面的数据完整保存。

2011年，Dziembowski等人[20]通过基于箭头图的铺石游戏（Pebbling Game），设计了新的原语“不可计算哈希函数（Uncomputable Hash Functions）”，并希望通过这种函数设计PoSE第二阶段的计算过程。该方法极大的减小了通信的复杂度，但很大程度地增加了验证者的验证负担。

2014年，Karvelas等人[21]分别通过基于超集中蝴蝶图簇（Butter?y Superconcentrator Family of Graphs）[22]的铺石游戏和函数求逆的方法，构造了两个新的PoSE方案。其中，与基于铺石游戏的方案Dziembowski等人的方案思想相同，但在效率上得到了一定的改善。而在基于函数求逆的方案中，验证者只需要一次正向计算来判断证明者给出的值是否正确，从而完全消除了验证者的验证压力。但相较于基于铺石游戏的方案，基于函数求逆的方法并没有很好的紧凑性。

2.2 可证明数据持有

为了解决分布式存储中数据是否被恶意篡改或丢弃的问题，人们提出了可证数据持有（Provable Data Precession，PDP）概念，以实现远程数据完整性检查。对于远程检查数据完整性的实现方法，一种自然的想法是从分布式数据库中下载数据，并在本地进行比对。但每次检查都需要网络将整个文件进行传输，增加了网络负荷。因此，如何在不下载全部数据的情况下检查远程数据的完整性，成为了一个关键的问题。

2003年，Deswarte等人[23]通过引入Diffie-Hellman协议[24]设计实现了远程完整性检查。此外，他们还设计了一个可实现远程完整性检查的函数结构。遗憾的是，Deswarte等人并没有给出这样一个具体方案。2006年，Gazzoni等人[25]通过引入RSA哈希同态函数，设计了Deswarte等人提出的函数结构，并由此设计了证明数据持有协议。

2007年，Giuseppe等人[26]为这一类远程数据完整性检查技术命名为“可证明数据持有”，并给出了完整定义。他们的方案将大文件分块并使用同态可验证标签技术对其进行标记，采取概率抽样验证方法避免对整个待验证文件进行计算，在保证安全性的同时提高了协议交互的效率。

同样在2007年，Juels等人[27]提出了“可恢复证明（Proof of retrievability，PoR）”方案，解决了远程数据完整性检查问题。他们将一些随机数据填充到文件中，并对文件进行纠错编码。如果远程数据被大范围改动，则可以通过随机数据的完整性检测出来;而如果只是文件中少数位发生变化，则可以通过纠错编码进行纠正。

为了实现远程动态数据完整性检查，Chris等人[28]提出了动态可证明数据持有（Dynamic Provable Data Precession，DPDP）方案。该方案通过基于秩的认证跳跃表，在实现原本PDP方案的基础上增加了远程更新和更新验证的过程，使得用户可以远程对数据进行增、删、改操作，并可对更新后的结果进行远程验证。

2.3 空间量证明

空间量证明是证明者P与验证者V之间的协议，协议要求P使V相信自己确实投入了一定量的磁盘资源。协议过程需要P根据V的要求构造一个相当大的随机文件，然后V再检查该随机文件的完整性以确保P确实生成并保存了该随机文件。与PDP/PoR等问题中涉及的数据完整性检查不同，验证者并不知道完整的数据内容，因而无法生成用于辅助验证的数据。为解决具体设计中存在的问题，Giuseppe等人与Dziembowski等人分别独立的构造了不同的PoSpace方案。

2014年，Giuseppe等人[16]基于铺石游戏和随机神谕假设，实现了单段PoSpace协议，其中协议包含两轮交互。该方案与Dziembowski等人提出的PoSE的方案[20]类似（事实上，Giuseppe等人的PoSpace方案也仅实现了PoSE的功能），不同的是：（1）Giuseppe等人利用铺石图自身结构的性质和Merkle树，大大降低了验证者的计算复杂度;（2）用堆式超集中蝶形图（Stack of Butter?y Superconcentrators）结合基本下限证明[29]，提高了方案的紧凑性。Giuseppe等人指出PoSpace有潜力作为PoW的替代方案，但遗憾的是，他们的方案每次执行都需要大量的时间构造随机文件，效率低下明显的限制了其应用。

2015年，基于同样的思想，Dziembowski等人[15]设计了两段PoSpace协议。该PoSpace协议具体可分为初始化阶段和执行阶段。初始化阶段与Giuseppe等人的单段PoSpace协议基本相同，需要完成随机文件和Merkle树的计算并检查文件的一致性。而在执行过程中，V同样需要生成随机挑战并发送给P，P根据挑战对应的标签返回对应的Merkle路径作为空间量证明。两段的PoSpace一定程度上更好的迎合了区块链系统的要求，但是两段协议使得方案的紧凑性明显下降。

基于对PoSpace中时空权衡问题的研究，2016年Ren等人[30]提出一种堆式二分扩展图作为铺石游戏中构造随机文件的结构。他们的方案表明，可以通过加节点之间的边数提高紧凑性，但这增加了图的复杂程度，降低了实用性。

2017年， Abusalah等人[31]舍弃了铺石游戏，而选择随机函数求逆作为PoSpace协议的底层问题，并基于Hellman的时空权衡攻击[32，33]做出了详细的讨论。基于随机函数求逆的PoSpace由于没有随机文件承诺过程且证明尺寸较小等特点，被认为比基于铺石游戏的PoSpace更适用于区块链系统中，但该方案在紧凑性上有很大的不足。

2.4 复制证明

假设验证者（用户）V希望将两段相同的数据D，D'存储至证明者（远程服务器）P中，则P可能仅存储D，每次进行数据完整性检查时快速生成D'，并根据PDP/PoR协议正确响应V的挑战。该问题主要是由于PDP/PoR方案无法解决远程数据备份存储问题，以及PDP/PoR方案没有公开可验证的性质。

2017年，Benet等人[34]提出了复制证明（Proof of Replicability，PoRep）作为解决方案。PoRep的主要思想是，通过编码生成与源数据内容不同但大小相同的副本并存储，并通过远程完整性检查来确保P确实存储了数据及其副本。同时，PoRep使用了PoSpace的两段结构解决可公开验证的问题。此外，他们的方案使用缓慢的伪随机置换（Pseudo-random permutation）函数计算副本，使得P不能快速通过原数据得到副本。

2018年，Alwen、Blocki和Pietrzak[36]研究出了一种具有更强性质的深度健壮图（Depth Robust Graphs，DRG）。同年，Pietrzak[35]提出使用该图的构造实现PoRep中的编码过程。这种编码本质上是利用铺石游戏构造出随机文件，再通过这些随机文件对存储文件进行编码。如此设计的编码过程确实减缓了计算副本的过程，但对副本进行恢复时也需要同样的过程，這使得效率十分低下。

同样在2018年，Fisch将深度健壮图与可验证延迟编码（Verifiable Delay Encode，VDE）相结合，构造了新的PoRep方案[37]。该方案使用了Bucket抽样算法[40]构造深度健壮图，使其具有很强的实用性。不同于Pietrzak的方案中仅保留部分节点标签，Fisch将整个图进行保存，再配合VDE快速解码的特性，明显提高了将副本恢复为原数据的效率。

2019年，Fisch基于PoRep方案的紧凑性考虑，基于对深度健壮图和堆式扩展二分图的研究[39]，设计了堆式深度健壮图并将其应用于PoRep协议设计中。其思想类似Ren等人[30]的分层结构，不同的是，每层中的节点形成一个深度健壮图。随着图的层数不断增加，理论上该方案的紧凑性可以也会无限提高，且深度健壮图自身的特性使得方案可以有效抵抗并行攻击。

3 空间量证明分类

针对当前对于空间量证明技术的研究，研究人员可以将其视为证明者P和验证者V之间的一个两段协议。为了讨论空间量证明协议的不同模型，本文介绍了Dziembowski等人给出的协议交互形式。整个空间量证明协议可以被划分为初始化和执行两个阶段，但由于不同的PoSpace方案之间使用的构造技术不同，从而使得每个阶段的交互目的存在一些差异。当前对PoSpace协议的研究主要可以分为两类：基于铺石游戏的PoSpace协议，基于函数求逆的PoSpace协议。

3.1 基于铺石游戏的PoSpace协议

3.1.1 铺石游戏与标签问题

铺石游戏是一种基于有向无环图（DAG）的分析时空复杂的技术。在铺石游戏中，铺石者需要用到黑色石头和白色石头，游戏要求铺石者根据铺石规则将石头放在DAG的顶点上。将有向无环图中的所有汇点（即没有后继的顶点）记为挑战集C，铺石者需要通过拓扑排序用石头铺满挑战集，方可获得游戏胜利。对于白色石头而言，有三条铺石规则。

（1）对于某一顶点，如果其所有前驱顶点上都有石头（白色或黑色），则可以将石头放在该顶点。

（2）对于某一顶点，如果它是源点（即没有前驱的节点），则可以将石头放在该顶点。

（3）每次铺石者只能将一块白色石头放在图上，但可以移除任意多个图上的白色石头。

基于铺石游戏的时空复杂度分析，将放置一块白色石头作为一次关键计算，将某一时间图上石头的个数记作当前消耗的空间量，铺石者总希望通过最少的计算和空间量完成游戏。与白色石头不同的是，黑色石头可以任意被放在图上。毫无疑问，可以用个黑色石头铺满挑战集，如此一来铺石者不需要计算步骤便可以获得游戏胜利。而铺石游戏中的时空权衡问题需要研究的是，是否存在使用个黑色石头的策略，使得通过T次铺石和同时最多个白色石头来获得游戏胜利。如果的值远小于且T的值又不太大，则这将是个很好的时空权衡策略，来实现用少量的时间换取空间。

在PoSpace协议中，铺石游戏是通过图标签问题来实现的。取图为DAG，其中为图中边的集合，为顶点的集合且。在图标签问题中，每一个顶点都对应与一个标签值，通过存储来模拟在顶点上铺石，通过删除来模拟将上的石头移除。此外，引入随机神谕来计算图上顶点的标签值，计算为：

其中，是表示铺石者身份的标识符，是前驱节点的索引。由公式（1）可知，对于非源点顶点，必须要计算其所有前驱的标签值，才能获得自己的标签值。由此，实现了模拟DAG中的拓扑序列。

3.1.2 基于铺石游戏的PoSpace协议结构

基于铺石游戏的PoSpace协议生成随机文件的过程，实际上是一个计算DAG顶点标签的过程，其随机文件的内容由DAG中頂点标签构成。在初始化阶段，证明者P会根据系统参数抽取一个DAG图，并将公钥作为自己的标识符，根据拓扑顺序计算并保存图G上对应挑战集顶点的标签。为了证明随机文件的完整性，证明者P将所有存储的挑战集顶点的标签值作为叶子结点，构建完整的Merkle树，并将Merkle树的根节点作为随机文件的承诺值发送给验证者V。随后V会通过一个“挑战-响应”过程，完成对随机文件完整性的检查。

在初始化的“挑战-响应”过程中，V随机抽取图上若干个顶点，将其作为挑战发送给证明者P。P的响应内容分为两部分：1）挑战节点的前驱节点的标签值（用于验证随机文件生成的正确性）;2）挑战节点及其前驱节点对应的Merkle路径（用于验证与承诺的一致性）。由于验证需要用到挑战节点前驱的标签值，而证明者P仅存储挑战集中的顶点标签，这意味此次验证过程需要重复一遍随机文件构造过程。

根据两段空间量协议的设计思想，执行阶段是一个需要反复运行的过程，因此执行阶段要比初始化阶段简单得多。执行阶段也是一个“挑战-响应”的过程，不同的是，V只能从挑战集中随机抽取顶点作为挑战，而P的响应也只是挑战节点对应的Merkle路径。具体协议为：

（1）初始化阶段

1）V和P分别获取相关参数和各自的公私钥对。

2）P根据系统参数、自己的公私钥、投入空间量N等生成自己的随机文件F。

3）构建F对应的Merkle树，并将树根作为F的承诺值发送给V。

4）V从整个DAG图中任意选取几个顶点，并将其作为挑战发送给P。

5）P重新执行生成文件F的操纵，并将挑战顶点及其前驱点的标签和Merkle路径作为响应，发送给V。

6）V验证响应的正确性。

（2）执行阶段

1）V从顶点挑战集C中随机选取几个顶点，并将其作为挑战发送给P。

2）P将挑战顶点对应的Merkle路径作为响应发送给V。

3）V验证响应的正确性。

3.1.3 基于铺石游戏的PoSpace安全性研究

基于铺石游戏的PoSpace协议的安全性很大程度依赖于DAG图的构造。由于铺石游戏本身存在时空权衡的现象，如何加强DAG中前驱节点与挑战集的依赖性，从而使得无法通过一定量的计算实现更少的空间存储，成为基于铺石游戏的PoSpace协议安全性研究的关键问题。

“空间差距（Space Gap）”是一种衡量不同方案间时空权衡能力的参数，其本质上是一个比值（N-N'）/N，其中N表示诚实证明者需要投入的空间量， 为敌手通过现有手段可获得的最小空间（也称为可证明的下界）。

Dziembowski等人[15]提出了两种图的结构来构造PoSpace协议，第一种基于Paul、Tarjan和Celoni[22]的图簇，第二种基于二分图、超集中图和Erdos、Graham、Szemeredi[41]的混合构造图。但是，Dziembowski的方案的空间差距至少为，如此大的空间差距使得协议的安全性无法得到保障。

2016年，Ren等人[30]提出一种堆式二分图来改善PoSpace协议的空间差距。堆式二分图可分为k层，各层分别为且每层包含n个节点。每层中每个节点恒定以d为出度，将边连接到下一层的节点上，使得每层之间形成一个随机二分图。堆式二分图确实大幅度的提高了空间差距，但理论上仍然存在的差距，且需要将无限增加d的取值作为代价。这极大程度的限制了方案的实用性。

Fisch[39]将堆式二分图的想法与深度健壮图结合起来，将其称为堆式深度健壮图，并将其用于PoRep协议中。随着构造堆式深度健壮图的迭代次数不断增加，理论上方案的空间差距将无限减少，这将允许对初始化阶段效率和安全性进行权衡。此外，堆式深度健壮图还可以有效地抵抗并行攻击。

3.2 基于函数求逆的PoSpace协议

3.2.1 基于函数求逆的PoSpace协议结构

基于函数求逆的PoSpace协议中存储的随机文件本质上是一个函数表，方案会事先设计一个反向求解困难的函数，要求证明者P通过穷举的方法正向计算出函数像与原像之间的对应关系并记录在函数表中。在初始化阶段，证明者P根据系统参数和自己的公钥计算函数表，其中函数域由P投入的空间量决定。在执行阶段，验证者V在函数域中抽取一个随机数作为挑战，P根据挑战值在函数表中找出相应的原像作为响应。具体协议过程为二个阶段。

（1）初始化阶段

1）V和P分别获取相关参数和各自的公私钥对，及函数像与原像的域。

2）P根据系统参数、自己的公私钥、投入空间量N等生成自己的函数表F。

（2）执行阶段

1）V选择随机数人r（mod N），并将其作为挑战发送给P。

2）P通过查找函数表F，找出对应的原像作为响应。

3）V验证响应的正确性。

3.2.2 基于函数求逆的PoSpace安全性研究

当前，只有Abusalah[31]提出了一个基于函数求逆的PoSpace协议，且基于Hellman的时空权衡攻击给出了安全性分析。Hellman的时空权衡攻击描述了这样一个过程：

（1）对于一个正向求解容易但反向求解困难的置换（为了避免发生碰撞，方案要求函数f是一个置换），取一个随机数x令，考虑序列其中;

（2）取N的一个因子T，证明者会存储所有的得到新的函数表，此时函数表的大小是原大小的1/T;

（3）对于一个随机挑战c，证明者对c递归的进行f置换，直到与某个发生碰撞;

（4）找到并递归的进行f置换，直到找到一个a使得，则将a作为对挑战c。

从上面的过程可以看出，一个正向求解容易的置换似乎总是可以通过上述过程，通过T次计算将存储量降低为原来的1/T，将敌手使用的空间大小记为S，则满足（表示忽略所有亚线性因子）。但实际上，正向求解容易似乎并不是基于函数求逆的PoSpace协议所必须的性质。

Abusalah设计了一个随机函数，其由函数和置换组成。将该随机函数定义为，其中（表示为编码取反）。该方案可以实现的安全性，而且可以通过对这种结构嵌套构造，实现的安全性。但是，这种方法构造的PoSpace协议的空间差距为，使得方案缺乏紧凑性。

3.3 两种方案对比

就当前研究进展而言，基于铺石游戏PoSpace方案的紧凑性远优于基于函数求逆PoSpace方案。从协议的交互过程上看，基于铺石游戏的PoSpace方案在初始化过程中比基于函数求逆的PoSpace方案多一个“挑战-响应”阶段，用于实现随机文件的完整性检查。这使得将PoSpace与区块链进行结合的时候，基于铺石游戏的PoSpace方案还需要有一个注册过程，用于提交承诺空间、随机文件的Merkle承诺等信息。而且在执行完整性检查的期間，提供证明的一方必须完整的执行一遍随机文件生成过程，这似乎对于无许可的公链而言有些不友好。此外，验证者在每次验证证明正确性，还需要获取提交承诺空间、随机文件的Merkle承诺等信息，这使得每次验证还需要回溯以前的块，而这些区块很可能极为久远。

通过分析执行阶段很容易发现，基于铺石游戏的PoSpace方案证明长度的规模比基于函数求逆的PoSpace方案要大很多。对于每一个标签的位置，基于铺石游戏的PoSpace方案的证明是一个Merkle路径，使得证明规模为O（logN）（N为投入的空间量）。但对于基于函数求逆的PoSpace方案而言，证明是一个函数原像，长度规模为O（1）。

虽然基于铺石游戏的PoSpace方案在紧凑性方面很有优势，但在具体实现上，区块链似乎对基于函数求逆的PoSpace方案更友好。

4 空间量共识与区块链

专用硬件的出现使得比特币系统中计算资源越来越集中，其产生的不公平性和能源浪费等问题也日趋严重。不同于比特币中将计算能力作为投入资源，以磁盘容量作为投入资源的PoSpace被视为一种解决这些问题的替代方案。然而将基于PoSpace的共识算法与区块链系统结合的过程中仍然面临着一些挑战。

4.1 空间量共识在区块链中的挑战

PoSpace与区块链系统结合的过程中挑战主要有两方面，“利益无关（nothing at stake）问题”和“竞争记账权问题”。与比特币中PoW不同，PoSpace的证明是从矿工存储文件中读取的某个随机数，这使得所有诚实矿工都可以在第一时间拿出合法的证明，因此什么样的证明可以在基于PoSpace的共识算法中获得记账权是一个关键的问题。

利益无关问题[42]是指生成区块所需证明的代价很低而产生的一系列安全性威胁。由于PoSpace生成证明的过程非常简单（仅从已保存的随机文件中读取），这使得当使用PoSpace替代PoW时很容易面临与PoStake一样的利益无关问题，而其中比较突出的攻击手段包括区块打磨攻击（Grinding attack）和长程攻击（Long-range attack）。

打磨攻击也可以分为两种情况。在第一种情况中，矿工通过调整区块中的可变内容使得下一个挑战更有利于自己。区块链系统中，所有矿工都会从上一个区块中获得随机挑战（通常是区块头的哈希值），此时研究人员将获取记账权的过程抽象成一个函数 ，记账权由f（x）值最高的矿工获得，其中x是矿工给出的空间量证明。矿工从自己的随机文件中读取相应的证明x并计算f（x）的值，如果矿工认为自己很大概率会在记账权竞争过程中获胜，则构造对应的区块头并反复调整区块头的内容，使得下一个由自己生成的证明x'也极有可能获胜。反复调整区块头内容的过程就是打磨过程，显然区块中有很多内容是允许打磨的，如时间戳和事务数量等。

第二种情况是在比特币中，每个矿工的计算能力有限，这使得矿工必须在多个分叉中选择一条链扩展。理性的矿工会要求自己选择扩展的链与大多数矿工的选择相一致，如此一来，另一条链将逐渐被系统遗忘。由于在基于PoSpace的共识算法中生成证明的过程非常容易，理性的矿工会选择同时对多个分叉链进行扩展，以避免自己选择的链被遗忘所带来的财产损失。而这样的结果将导致分叉永远存在，且多个分叉会以同样的速度延伸，从而导致系统永远无法达成共识。

长程攻击是指矿工对很早之前的区块发起分叉攻击，并构造一条链来代替主链。在比特币系统中，矿工根据链的长度来判断主链，当个人算力无法超过50%时，矿工用永远无法通过长程攻击构造一条链来取代主链。但在基于PoSpace的共识算法中，任意矿工都可以生成一条足够长的链，这使得比特币中的方法行不通。方便起见，这里将矿工判断主链的过程也抽象成一个函数F（·），显然F（·）的值应该是与链上每一个区块f（·）值相关。但矿工似乎总可以通过第一种打磨攻击构造一条链，且链上的每个区块的f（·）值都很高，這极大程度的威胁了共识算法的安全性。

由于利益无关问题是由产生证明的过程太容易所造成的，因此增加证明产生的难度成为了解决该问题的主要方式。为了使矿工在一段时间内（一个挖矿周期中）只能产生有限的证明数量，许多方案往往会将时间作为一个参考量融入到证明中，因此提出了时空量证明（Proof of SpaceTime，PoST）。当前，已经有许多基于PoSpace协议的区块链系统，如Spacemesh、Filecoin和Chia。他们都无一例外的提出了PoST的概念，但它们实现的方式都不相同，甚至在概念上也存在很大的差异。当然，也有非PoST解决方案，如Spacemint协议，它们同样给基于PoSpace的区块链系统提出了许多有意义的方案。对于不同系统解决问题的方案如表1所示。

4.2 Spacemint

2018年，Park等人提出了一个基于PoSpace的区块链协议—Spacemint[17]。协议给出一个判断记账权和最佳链的具体方案，并基于对利益无关问题的分析给出了相应的解决方案。

在判断记账权和最佳链的方案中，Spacemint引入了“质量”的概念。在竞争记账权的过程中，验证方会比较不同区块的质量大小，并将质量最大的区块作为候选区块记在区块链上。而方案中的链质量是由链上所有区块的质量按一定权重乘在一起的结果。

为了抵抗第一种打磨攻击，Spacemint对区块的结构进行分割。整个区块被分割成哈希部分、签名部分和事务部分，不同部分之间通过签名相互关联。该结构将原本区块头中允许打磨的内容从哈希部分移到前面部分中，并将哈希部分的哈希值作为下一个区块的随机挑战，以此来抵抗块打磨攻击。出于对第二种打磨攻击的考虑，Spacemint引入惩罚机制，并设计适当激励措施使所有矿工对系统进行监督，并举报恶意行为。

至于长程攻击，Spacemint提出让一个区块的哈希部分作为此后多个区块的挑战来源。例如，区块i的哈希部分的哈希值c，将为其后的次记账权竞争生成随机挑战，如此一来，矿工就不能通过调整区块内容来获得更有利于自己的挑战。

此外，Spacemint中调整了基于铺石游戏PoSpace的交互过程。原本基于铺石游戏PoSpace的交互过程中，初始化阶段需要完成随机文件生成和文件完整性证明两个过程。在Spacemint的初始化阶段中，矿工仅完成随机文件生成然后就开始执行阶段，而文件完整性证明则在成功获得记账权后随完整区块一起提交给区块链。这样做的优点是多次检查文件完整性，提高了系统的安全性。但缺点是每一次文件完整性证明生成的过程相当于重新生成随机文件的过程，这种效率对于实际的系统而言是不可能接受的。

Spacemint确实为基于PoSpace系统设计提出了许多有用的建议，但仍然有一些问题解决的不够优雅（如，抵御第二种打磨攻击采用的惩罚机制），这使得该协议离实际部署仍有一定差距。

4.3 Chia

Chia是由Cohen和Pietrzak[43]提出的一种基于函数求逆PoSpace的共识方案，目前作为Alpha电子货币的底层协议，该项目一定程度上借鉴了Spacemint的处理方法，但在许多问题的处理上比Spacemint更加实用。

Chia在解决竞争记账权的问题时引入了PoST的概念。在Chia网络中除了有矿工负责打包区块之外，还有时主需要确认矿工生成的空间量证明。时主确认证明时采用的技术是VDF[44]，不同于Fisch方案中数据编码的作用，此处是利用了VDF计算过程缓慢的性质，使得确认一个合法的证明需要消耗一些时间资源。在竞争记账权的过程中，矿工产生空间证明后需要交由时主确认，而后才能被记入区块链中。Chia借用了Spacemint中区块质量的概念，要求时主确认证明的速度与证明的质量有关，这使得质量越优的区块越容易被确认，从而获得记账权。

在对抗第一种打磨攻击的方法上，Chia除了采用Spacemint的区块分割方式之外，还要求哈希部分的密码原语均具有唯一性，以防止矿工对签名、证明值或VDF输出进行打磨。对于第二种打磨攻击，Chia采取的方案是允许矿工对分叉的多条链进行延伸。对于时主而言，每个竞争周期他们只会确认k个证明（由于网络延时的原因，可能存在每个周期确认证明数量多于k的情况）。k的值设置的越大，越能保证系统的安全性，但随着k的增加，每个周期矿工的负担也在增加，Chia的开发团队认为k=3是一个较为合理的权衡。

另外，由于VDF是一個计算缓慢的技术，其似乎天然具有抵抗长程攻击的优势。这使得在Chia中，矿工几乎不可能以很快的速度产生一条当前链的替代链。

4.4 Spacemesh

Spacemesh是一个将用户投入的空间资源和投入时长综合考虑的共识协议，当前也作为电子货币系统的底层协议。该项目开创性的使用网状结构代替常见的链状结构，为区块链研究提供了许多开创性的思路。

与Chia中增加证明生成难度的目的不同，Spacemesh中提到的PoST[45，46]概念强调矿工或投入一定量空间，或消耗一定量的计算能力。与PoSpace不同的是，PoST允许矿工对存储的数据进行时空权衡，但根据其理性存储证明保证了一个理性矿工必然选择存储完整数据作为资源投入（即，存储完整数据的代价最小）。此外，PoST并不使用类似于铺石游戏的空间难解函数，而是通过不可压缩工作量证明（Incompressible Proofs of Work，IPoW）计算随机文件。IPoW强调的不可压缩性使得矿工无法通过少量存储节省计算时间，即每一块数据的丢失都必须通过完整的计算重新获得，提高了删除部分文件的代价。为了证明矿工投入资源用掉的时间，Spacemesh引入了消逝时间证明（Proof of Elapsed Time，PoET），该技术可以证明从矿工得到初始挑战到现在所用的时间。最终，将PoET和PoST组合并结合Fiat-Shamir技术，从而实现了非交互时空证明（Non-Interactive Proofs of Space-Time），该证明可确保矿工确实在一定时间内投入了一定量的空间。

对于竞争记账权问题，协议要求每个矿工进入系统时都需要对自己的身份进行注册，系统会将所有的注册身份汇成一张身份表存储在注册节点上。在每层竞争记账权的过程中，每个矿工先通过一个统一的随机函数计算出身份表上的一个子集，然后在这些矿工生成的区块中选出超过阈值的区块记录在区块链上。这一思想类似于Chia中，对每个周期确认证明数量k的控制，因此同样具有防止第二种打磨攻击的作用。此外，方案结合拜占庭算法提出了“龟兔共识（tortoise and hares consensus）”协议[48]，由此确保诚实者的资源都集中在同一条链上，从而有效地抵抗长程攻击。

4.5 Filecoin

Filecoin[48]是一个基于PoRep协议[34]设计的文件存储与检索系统。系统中包含用户、存储矿工和检索矿工三种角色，其中用户需要使用系统存储或获取数据，存储矿工通过帮助用户存储数据来获得服务费，而检索矿工通过帮助用户获取数据来获得服务费。但只有存储矿工才能产生新的区块，检索矿工需要根据请求寻找存储对应资源的存储矿工，并要求其提供数据服务。

Filecoin在竞争记账权阶段采用了“期望共识（Expected Consensus）”的方法，该方法要求在每个周期中，区块链系统会选取小部分人获得记账权，人数的期望为1。但在某个阶段中，选取的人数可能为0或2。如果为0则由系统添加一个空块;如果为2则会类似于比特币，较少人选择的链将会被人遗忘。对于矿工而言，它们需要在每个竞争周期检查自己是否被选中，检查方法类似CoA[49]、Snow White[50]或Algorand[51]。

Filecoin中也存在PoST的概念，其通过反复读取随机文件来增加矿工产生证明的复杂程度。Filecoin中的PoST本质上是一个证据链，矿工根据区块链系统中给出的挑战计算第一个证明，再根据第一个证明的哈希值计算的二个证明，依次计算出完整的证据链。证据链的串行计算对长程攻击和第二种打磨攻击都能起到一定的抵御作用。

5 结束语

空间量证明作为工作量证明的一种替代方案，其节省能源和公平的特性吸引了许多研究学者的青睐。本文对一些存储证明技术进行介绍，并对空间量证明的研究进行详细的梳理与分析。此外，文章希望给专注于共识算法的研究人员一个新视角，并对后续的研究起到启发和借鉴作用。

综合现有的对空间量证明的研究来看，大致可以分为三个方向，分别为功能研究、紧凑性研究和工程研究。

在功能研究上，一个重要的成果就是PoRep协议。该协议使得矿工在贡献磁盘空间时，不再存储一些无意义的随机文件，而是有意义且可恢复的文件。一个简单的想法是，基于该技术开发的区块链系统不再把存储区块作为一种负担，而将其作为自己获取奖励的资源。此外，可以结合DPDP技术，在保证远程数据存储安全性的同时增加动态性，使得区块链系统不只提供存储服务，还可以动态产生或删除一些用户数据。

在紧凑性研究上，基于铺石游戏的PoSpace方案已经取得了一些理论成就，但将具有完美紧凑性的PoSpace投入应用还有些距离。另一方面，由于区块链对基于函数求逆的PoSpace方案更友好，因此提高基于函数求逆PoSpace的紧凑性将非常有意义。

在工程研究上，协议的安全和效率是永恒的话题。虽然基于PoSpace的区块链系统已经开始部署，但单从理论上难以判断其成功与否。对各类区块链系统需要不断发掘可能出现的恶意行为，并研究对抗策略。通过不断尝试引入新的密码技术，完善人们对系统的需求。

参考文献

[1] Nakamoto S. Bitcoin： A peer-to-peer electronic cash system[J]. 2008.

[2] Underwood S. Blockchain beyond bitcoin[J]. Communications of the ACM， 2016， 59（11）： 15-17.

[3] Mettler M. Blockchain technology in healthcare： The revolution starts here[C]//2016 IEEE 18th International Conference on e-Health Networking， Applications and Services （Healthcom）. IEEE， 2016： 1-3.

[4] Dorri A， Kanhere S S， Jurdak R， et al. Blockchain for IoT security and privacy： The case study of a smart home[C]//2017 IEEE international conference on pervasive computing and communications workshops （PerCom workshops）. IEEE， 2017： 618-623.

[5] Mital R， de La Beaujardiere J， Mital R， et al. Blockchain application within a multi-sensor satellite architecture[J]. 2018.

[6] 袁勇，倪曉春，曾帅，等.区块链共识算法的发展现状与展望[J].自动化学报， 2018， 44（11）： 2011-2022.

[7] De Vries A. Bitcoin's growing energy problem[J]. Joule， 2018， 2（5）： 801-805.

[8] King S， Nadal S. Ppcoin： Peer-to-peer crypto-currency with proof-of-stake[J]. self-published paper， August， 2012， 19.

[9] Larimer D. Delegated proof-of-stake （dpos）[J]. Bitshare whitepaper， 2014.

[10] Dwork C， Naor M. Pricing via processing or combatting junk mail[C]//Annual International Cryptology Conference. Springer， Berlin， Heidelberg， 1992： 139-147.

[11] Abadi M， Burrows M， Manasse M， et al. Moderately hard， memory-bound functions[J]. ACM Transactions on Internet Technology （TOIT）， 2005， 5（2）： 299-327.

[12] Dwork C， Goldberg A， Naor M. On memory-bound functions for fighting spam[C]//Annual International Cryptology Conference. Springer， Berlin， Heidelberg， 2003： 426-444.

[13] Dwork C， Naor M， Wee H. Pebbling and proofs of work[C]//Annual International Cryptology Conference. Springer， Berlin， Heidelberg， 2005： 37-54.

[14] Percival C. Stronger key derivation via sequential memory-hard functions[J]. 2009.

[15] Dziembowski S， Faust S， Kolmogorov V， et al. Proofs of space[C]//Annual Cryptology Conference. Springer， Berlin， Heidelberg， 2015： 585-605.

[16] Ateniese G， Bonacina I， Faonio A， et al. Proofs of space： When space is of the essence[C]//International Conference on Security and Cryptography for Networks. Springer， Cham， 2014： 538-557.

[17] Park S， Kwon A， Fuchsbauer G， et al. Spacemint： A cryptocurrency based on proofs of space[C]//International Conference on Financial Cryptography and Data Security. Springer， Berlin， Heidelberg， 2018： 480-499.

[18] Alwen J， Chen B， Kamath C， et al. On the complexity of scrypt and proofs of space in the parallel random oracle model[C]//Annual International Conference on the Theory and Applications of Cryptographic Techniques. Springer， Berlin， Heidelberg， 2016： 358-387.

[19] Perito D， Tsudik G. Secure code update for embedded devices via proofs of secure erasure[C]//European Symposium on Research in Computer Security. Springer， Berlin， Heidelberg， 2010： 643-662.

[20] Dziembowski S， Kazana T， Wichs D. One-time computable self-erasing functions[C]//Theory of Cryptography Conference. Springer， Berlin， Heidelberg， 2011： 125-143.

[21] Karvelas N P， Kiayias A. Efficient proofs of secure erasure[C]//International Conference on Security and Cryptography for Networks. Springer， Cham， 2014： 520-537.

[22] Paul W J， Tarjan R E， Celoni J R. Space bounds for a game on graphs[J]. Mathematical systems theory， 1976， 10（1）： 239-251.

[23] Deswarte Y， Quisquater J J， Sa?dane A. Remote integrity checking[C]//Working Conference on Integrity and Internal Control in Information Systems. Springer， Boston， MA， 2003： 1-11.

[24] Diffie W， Hellman M. New directions in cryptography[J]. IEEE transactions on Information Theory， 1976， 22（6）： 644-654.

[25] Gazzoni Filho D L， Barreto P S L M. Demonstrating data possession and uncheatable data transfer[J]. IACR Cryptology ePrint Archive， 2006， 2006： 150.

[26] Ateniese G， Burns R， Curtmola R， et al. Provable data possession at untrusted stores[C]//Proceedings of the 14th ACM conference on Computer and communications security. 2007： 598-609.

[27] Juels A， Kaliski Jr B S. PORs： Proofs of retrievability for large files[C]//Proceedings of the 14th ACM conference on Computer and communications security. 2007： 584-597.

[28] Erway C C， Küp?ü A， Papamanthou C， et al. Dynamic provable data possession[J]. ACM Transactions on Information and System Security （TISSEC）， 2015， 17（4）： 1-29.

[29] Tompa M. Time-space tradeoffs for computing functions， using connectivity properties of their circuits[J]. Journal of Computer and System Sciences， 1980， 20（2）： 118-132.

[30] Ren L， Devadas S. Proof of space from stacked expanders[C]//Theory of Cryptography Conference. Springer， Berlin， Heidelberg， 2016： 262-285.

[31] Abusalah H， Alwen J， Cohen B， et al. Beyond Hellmans time-memory trade-offs with applications to proofs of space[C]//International Conference on the Theory and Application of Cryptology and Information Security. Springer， Cham， 2017： 357-379.

[32] Hellman M. A cryptanalytic time-memory trade-off[J]. IEEE transactions on Information Theory， 1980， 26（4）： 401-406.

[33] Fiat A， Naor M. Rigorous time/space tradeoffs for inverting functions[C]//Proceedings of the twenty-third annual ACM symposium on Theory of computing. 1991： 534-541.

[34] Benet J， Dalrymple D， Greco N. Proof of replication[J]. Protocol Labs， July， 2017， 27： 20.

[35] Pietrzak K. Proofs of catalytic space[C]//10th Innovations in Theoretical Computer Science Conference （ITCS 2019）. Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik， 2018.

[36] Alwen J， Blocki J， Pietrzak K. Sustained space complexity[C]//Annual International Conference on the Theory and Applications of Cryptographic Techniques. Springer， Cham， 2018： 99-130.

[37] Fisch B. PoReps： Proofs of Space on Useful Data[J]. IACR Cryptology ePrint Archive， 2018， 2018： 678.

[38] Boneh D， Bonneau J， Bünz B， et al. Verifiable delay functions[C]//Annual international cryptology conference. Springer， Cham， 2018： 757-788.

[39] Fisch B. Tight proofs of space and replication[C]//Annual International Conference on the Theory and Applications of Cryptographic Techniques. Springer， Cham， 2019： 324-348.

[40] Alwen J， Blocki J， Harsha B. Practical graphs for optimal side-channel resistant memory-hard functions[C]//Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security. 2017： 1001-1017.

[41] Erdoes P， Graham R L， Szemeredi E. On sparse graphs with dense long paths[M]. Stanford University. Computer Science Department， 1975.

[42] Martinez J. Understanding proof of stake： the nothing at stake theory[J]. 2018.

[43] Cohen B， Pietrzak K. The Chia Network Blockchain[J]. 2019.

[44] Pietrzak K. Simple verifiable delay functions[C]//10th innovations in theoretical computer science conference （itcs 2019）. Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik， 2018.

[45] Moran T， Orlov I. Rational proofs of space-time[J]. Cryptol. ePrint Arch.， Tech. Rep， 2016， 35.

[46] Moran T， Orlov I. Simple proofs of space-time and rational proofs of storage[C]//Annual International Cryptology Conference. Springer， Cham， 2019： 381-409.

[47] Bentov I， Hubácek P， Moran T， et al. Tortoise and Hares Consensus： the Meshcash Framework for Incentive-Compatible， Scalable Cryptocurrencies[J]. IACR Cryptology ePrint Archive， 2017， 2017： 300.

[48] Benet J， Greco N. Filecoin： A decentralized storage network[J]. Protoc. Labs， 2018.

[49] Bentov I， Lee C， Mizrahi A， et al. Proof of activity： Extending bitcoin's proof of work via proof of stake [extended abstract] y[J]. ACM SIGMETRICS Performance Evaluation Review， 2014， 42（3）： 34-37.

[50] Bentov I， Pass R， Shi E. Snow White： Provably Secure Proofs of Stake[J]. IACR Cryptology ePrint Archive， 2016， 2016（919）.

[51] Micali S. Algorand： the efficient and democratic ledger （2016）[J]. arXiv preprint arXiv：1607.01341， 2017.