一种Petri网优化的验证码识别方法

马金林,陈德光,马自萍,魏 麟

(北方民族大学 计算机科学与工程学院,银川 750021)

0 概述

随着互联网技术的飞速发展,验证码(CAPTCHA)识别已成为判别人机身份的有效手段,担负着保护网络账号安全的第一道屏障,用于防止网站被自动程序进行大批量的恶意攻击[1]。基于此,验证码识别技术的研究有益于验证各种验证码的安全性,帮助人们设计更可靠、安全的验证码。

传统的验证码处理流程可分为验证码预处理、二值化、去除离散噪声、字符分割、归一化、特征提取、训练和字符识别等步骤[2]。这些步骤相对独立,整个流程较为复杂,其对粘连较低、噪声较小的验证码图片效果明显,而对于字符相互堆叠、扭曲度较高的验证码效果不理想。近年来,随着深度学习的兴起,有学者提出采用深度神经网络的方法实现噪音较大的验证码识别,并取得了较好的成果。文献[3]提出的基于两极DCNN架构的模型能将形变度较大的验证码识别准确度提升至95%以上,但是其模型的参数量与浮点数计算量偏高。文献[4]提出的自适应中值滤波算法经过多次迭代后平均准确度达到98%以上,但是其步骤较多相对繁琐。文献[5]提出的方法对极其复杂验证码的识别率达到82%左右,但是验证码复杂性还缺少评判标准。

神经网络的特征提取与训练过程类似于“黑箱”操作,若要得到识别率高的结果,需要针对网络结构以及模型参数进行大量的繁琐调整,而在国内外研究过程中,通常情况下直接给出模型的合理结构与最优参数值,并未对结构和参数值的探索过程进行合理的解释,致使网络的泛化能力较差且不便于后续改进。同时,在以往的验证码识别系统中,模型优劣的评判标准更注重准确度,并未讨论该模型所需参数量与浮点数计算总量,存在一定的局限性。

针对上述问题,本文提出一种基于深度卷积神经网络的验证码识别方法。在研究神经网络模型结构的基础上,运用Petri网建模,并利用Petri网的相关理论分析该模型内部组成及相互关联的关系。在此基础上,提出模型的优化策略并通过相关实验验证优化策略的正确性。同时,针对模型参数量与浮点数计算量之间的关系,提出超活性概念,以对不同模型进行灵敏度分析。

1 卷积神经网络和Petri网

1.1 卷积神经网络

卷积神经网络(Convolutional Neural Network,CNN)是一种建立在传统神经网络基础上的深度神经网络[2,6]。在结构上其通常由卷积层、池化层、激励函数(通常使用线性整流单元)及全连接层组成[7]。图1为CNN结构。

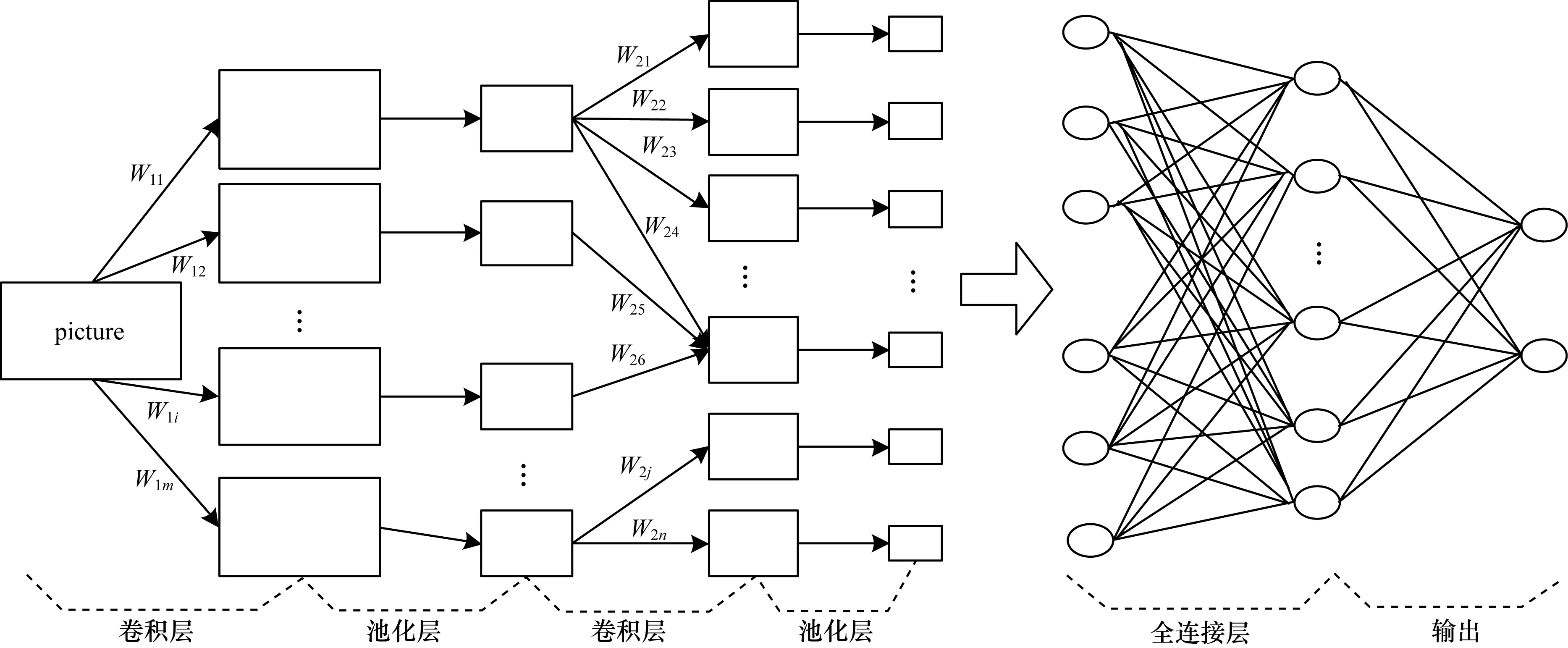
图1 CNN结构

1.2 Petri网

Petri网是离散并行系统的数学表示,其用于描述异步并发的系统模型[8-9],它既具有严格的数学表述方法,同时也具有直观的图形表示方法[10]。为了支撑CNN模型,需要利用先进的信息化技术手段对其建模。由于CNN是发生在训练周期内的活动,因此可参照Petri网的概念,即以基本网(EN-net)系统为基础,从而逐步扩展为符合卷积神经模型的网络结构,进而优化网络结构与参数以提高验证码识别准确度。借助Petri网重要的理论和关键技术,并根据EN-net的定义,可对CNN模型给出以下定义:

定义1卷积神经基本网(CNE-net)系统是由四元组N=(P,T,F,M0)组成。其中:P={P0,P1,…,Pm}为有限库所的集合,每个库所包含一批验证码资源;T={T0,T1,…,Tn}为有限变迁的集合,每个变迁的发生代表当前库所的资源流向下一个库所,且当前库所中不会剩余资源;F为流关系,即库所与变迁之间关系的集合,为库所与变迁的笛卡尔积,代表当前阶段训练完成后的信息输出到后续库所中,以方便后续工作开展[11];M0为初始情态,即在初始情况下各个库所的资源分布情况。在此基础上,CNE-net网络还应满足以下条件:

1)P∪T≠∅,即库所与变迁至少存在一类,它们不能同时为空。

2)P∩T≡∅,即库所与变迁是2类元素,不能交叉。

3)F⊆(P×T)∪(T×P),即流关系F既可以由库所流向变迁也可以由变迁流向库所。

4)M0⊆2p,即M0为初始情态,表示初始情况下各库所的资源分布情况。

5)dom(F)∪cod(F)≡P∪T,即流关系F的定义域dom(F)与值域cod(F)的并集为库所P与变迁T的并集,用符号表示为dom(F)={x|∃y:(x,y)∈F},cod(F)={y|∃x:(x,y)∈F}。

2 Petri网模型优化

2.1 AlexNet网络结构

AlexNet网络设计结构如图2所示,其由5层卷积、3层池化、3层全连接构成。AlexNet网络中每层的参数如表1中的AlexNet所示。 基于AlexNet网络并根据定义1的CNE-net,给出其对应的Petri网模型,如图3所示,其模型元素与对应的流程如表2所示。

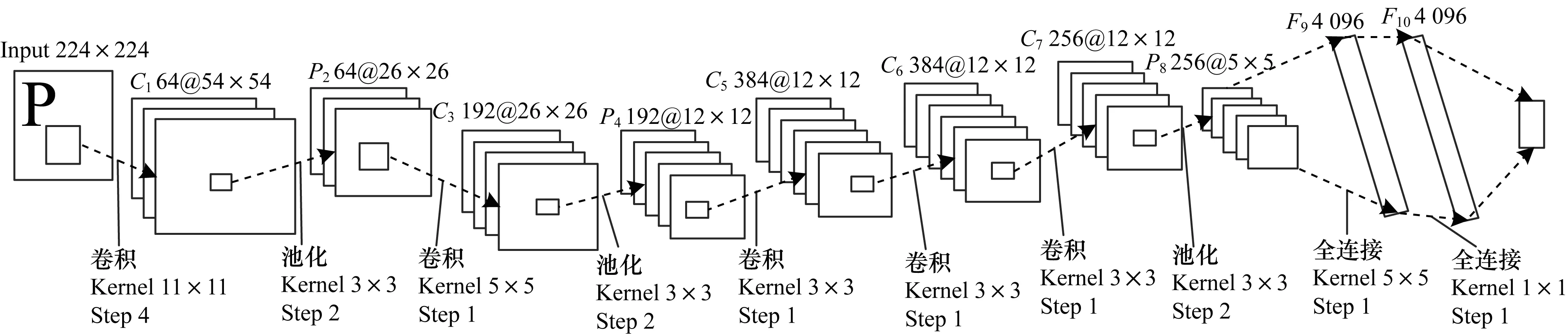
图2 AlexNet网络结构

表1 AlexNet各层参数设置

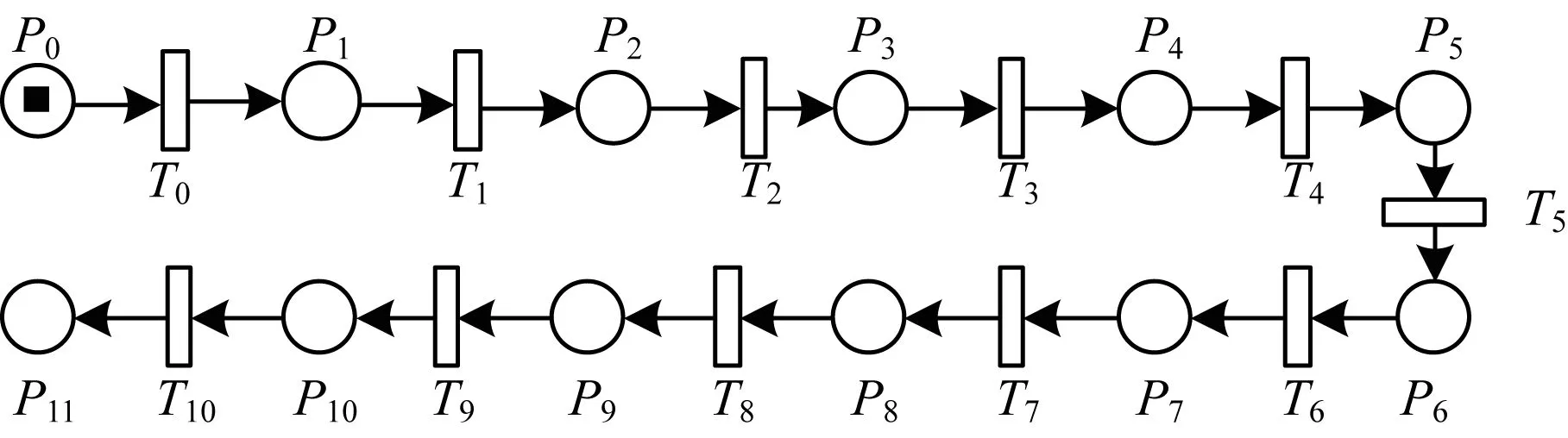
图3 基于AlexNet的Petri网模型

表2 AlexNet的Petri网模型流程

由上述Petri网结构可知,其类似于一个出现网,而出现网仅是将发生过程按时间顺序进行排列,因此其不足以优化AlexNet网络模型。基于AlexNet网络的特殊性,并结合CNE-net,下文给出AlexNet网络的Petri网优化方法。

2.2 基于Petri网参数优化的AlexNet

2.2.1 预备知识

预备知识主要有以下4个方面:

1)发生权。t∈T,M为N的标识,t在M下有发生权,记作M[t>[12],且满足以下条件:

(1)∀s∈·t:M(s)≥W(s,t),即s在t变迁前驱发生的条件为s库所中的资源要大于等于所需要消耗的资源。

(2)∀s∈t:M(s)+W(s,t)≤K(s),即库所s的容量K要大于等于原库所中的资源容量加上该变迁所产生的资源容量。

2)后继。若M[t>,即t在M条件下具有发生权,M′记为M的后继,后继关系记为M[t>M′[13],且满足以下条件:

(1)如果s∈·t-t·,则M′(s)=M(s) -W(s,t),即s库所要消耗资源W(s,t)。

(2)如果s∈t·-·t,则M′(s)=M(s) +W(s,t),即s库所要生成资源W(s,t)。

(3)如果s∈·t∩t·,则M′(s)=M(s)+W(t,s) -W(s,t),即s库所既要生成资源W(t,s),又要消耗资源W(s,t)。

(4)如果s∉·t∪t·,则M′(s)=M(s),即s库所既不生成资源,也不消耗资源。

3)前集与后集。对于x∈P∪T,若有:

(1)·x={y|y∈P∪T∧(y,x)∈F},则称·x为x的前集[14]。

(2)x·={y|y∈P∪T∧(x,y)∈F},则称x·为x的后集[14]。

4)公平性。对于t1,t2∈T,若存在正整数k,使得∀M∈R(M0)和∀σ∈T*:M[σ>有#(ti/σ)=0↔#(tj/σ)≤k,i,j∈{1,2}且i≠j,则称t1和t2处于公平关系[15]。

2.2.2 基于Petri网参数优化的AlexNet网络

定义2Petri网参数优化的AlexNet(Petri-ANPP-net)由六元组Π=(P,T;F,K,W,M0)组成,其中N=(P,T;F,M0)为定义1中卷积神经的基本网系统,其在满足基本网系统的前提下还满足以下条件:

1)Π中有一个开始位置i∈P和一个结束位置o∈P。

2)K为库所P元素的容量函数,其代表验证码图片批次的大小,即有K:P→{1,2,3,…}∪{∞}。

3)W为流关系F上的权函数,其代表验证码图片的产生或消耗的量多少,本文采用学习率来表示流关系,即有W:F→{1,2,3,…}。

4)M0为初始资源分布情况,且还应该满足∀s∈S:M0(s)≤K(s)。

5)具有合理性,即:Π具有安全性,在任何时刻,Π中的所有库所中至少包含一类验证码资源;具有规范性,任何库所P均有容纳资源(token)多少的表示,而非用一个token表示一类资源,这样的Petri网描述能力更强。同理,每个变迁t均具有发生权M[t>和后继M[t>M′;Π不包含无法执行的死任务,即从开始位置{i}起,任何一个变迁均可以被激活用来执行任务。

2.3 基于Petri网结构优化的AlexNet

Petri网是一个异步并发系统,而定义2中Petri-ANPP-net给出的Petri网模型是一个顺序执行系统且系统参数较多,将顺序执行系统扩展为异步并发系统且减少参数的量。由并发公理可知,系统性能将会得到进一步改善且网络更容易解读。

定义3Petri网结构优化的AlexNet(Petri-ANPS-net)是四元组Σ=(S,T,W′,M0),其中,S,T,M0与Petri-ANPP-net中相同,其应满足以下条件:

1)如果对于∀(x,y)∈S×T∪T×S,即当(x,y)∈F时,有W′(x,y)=W(x,y),则称W′:S×T∪T×S→{0,1,2,…}为Σ的广义权函数[16]。

2)如果M[t>发生,则∀s∈S:M(s)≥W′(s,t)且M(s)+W′(s,t)≤K(s)[16-17],即变迁t在M标识下具有发生权的条件为库所s中的token要大于等于所消耗的token数量,且库所s中所容纳的token数量要大于等于其原本库所中的数量加上新产生的token数量。

3)如果M[t>M′发生,则M[t>且∀s∈S,有M′(s)=M(s)+W′(t,s)-W′(s,t)][18-19],即M若有后继M′,则应满足t在M下有发生权,且M′的token数量为原库所中的token数量加上产生的token数量再减去消耗的token数量。

4)由于Petri-ANPS-net是异步并发系统,且每个验证码字母地位相当,则当其并发时,各个子系统间的权重相同。

为使更改后的模型与原模型变动最小,在图3模型中P9库所后设置4组并发操作(这是因为验证码的字符长度为4)。并发操作完成后,汇聚于漏库所O。这样改进后,将原来的顺序执行系统变为异步并发系统,具体优势有以下3点:

(1)模型简洁,由定义2的Petri-ANPP-net六元组改造为定义3的Petri-ANPS-net的四元组,降低了模型的复杂度。

(2)模型参数更新合理化,P10～P13共享P9中的token,但是各个分支的关系相互独立,则各个分支的权值与偏置值的更新与其余分支无关。

(3)加速模型收敛,由于异步并发系统中4条分支同时训练,相对于顺序执行收敛速度更快。

图4所示为基于ANPS-net的模型(黑色变迁为隐变迁,表示前面的若干库所与变迁,由于图4中前面的库所变迁与图3中的P0～P9相同,因此采用隐变迁代替)。相关参数见表1(右)表示的Petri-ANPS-net网络结构。

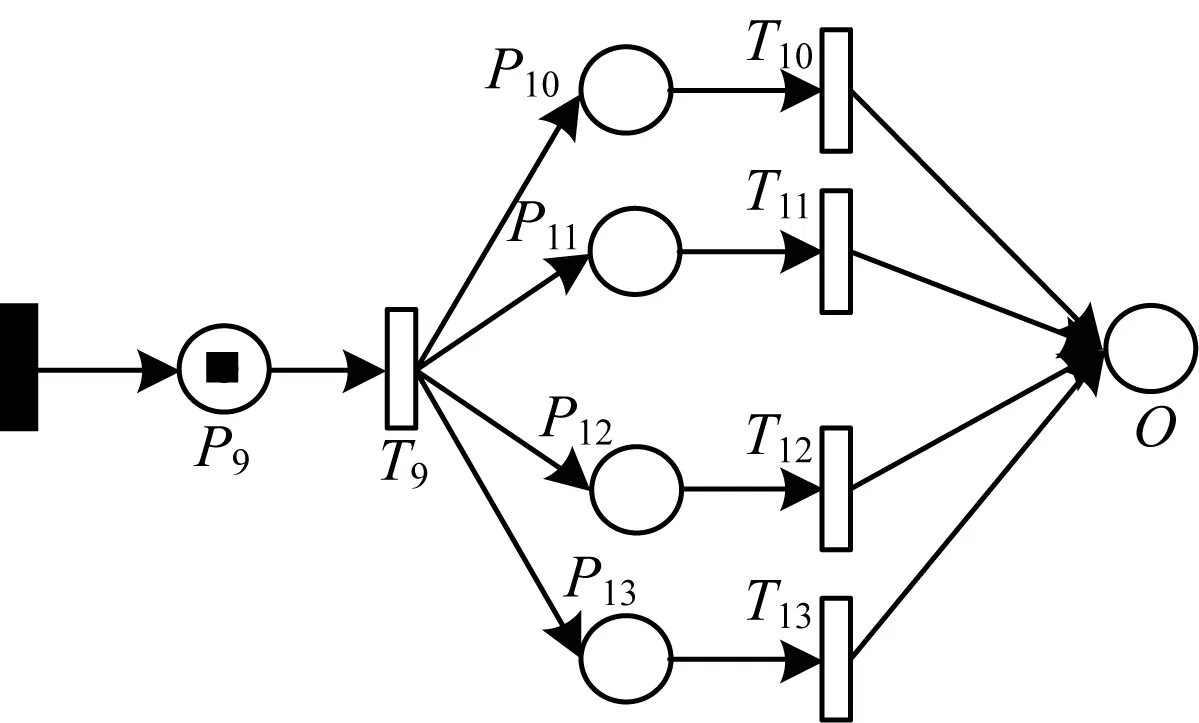
图4 Petri-ANPS-net模型

2.4 基于Petri网优化的DenseNet-BC

2.4.1 DenseNet网络

密集型卷积神经网络DenseNet由文献[20]提出,其从神经网络的特征入手,简化模型参数,同时达到了更好的效果。它的主要思想是跨层连接,网络的每一层输入都是前面所有层输出的并集,而该层学习到的特征也会被直接传给后面所有层作为输入。在上述过程中,信息流进行整合,避免了信息在层与层之间传递丢失的问题,极大地减轻了梯度弥散。

DenseNet主要由密集块和过渡层组成。在每个密集块内,层与层之间的非线性转换函数Hl(·)包含3个连续操作,即批量标准化、线性整流函数ReLU以及3×3 卷积(3×3Conv)[20]。 定义超参数k为增长率,如果Hl(·)每层产生k个特征映射,则第l层将有k0+k(l-1)个特征映射输入(k0为首个输入层的特征数)。

2.4.2 DenseNet-BC网络

DenseNet网络的密集连接方式会导致后续密集层有大量输入特征,从而导致参数量急剧增长,因此在每个密集层的3×3Conv前引入1×1Conv作为颈瓶层,来减少特征映射输入的数量[21],同时,在每个过渡层中引入一个1×1Conv使其输出特征减少,以增强GPU内存的利用率。

由于实现朴素的DenseNet-BC可能需要大量的GPU内存,基于此,引入共享内存分配机制,所有层都使用共享内存分配来存储中间结果。后续图层会覆盖先前图层的中间结果,但可以在后向传递期间以最低成本重新填充它们的值,这样做可以将特征映射内存消耗从二次减少到线性。图5所示为DenseNet-BC网络结构模型,由3个密集块与2个过渡层组成,图6第3列为DenseNet-BCm网络参数,图6第4列、第5列给出Petri-DNBC-net的网络参数。

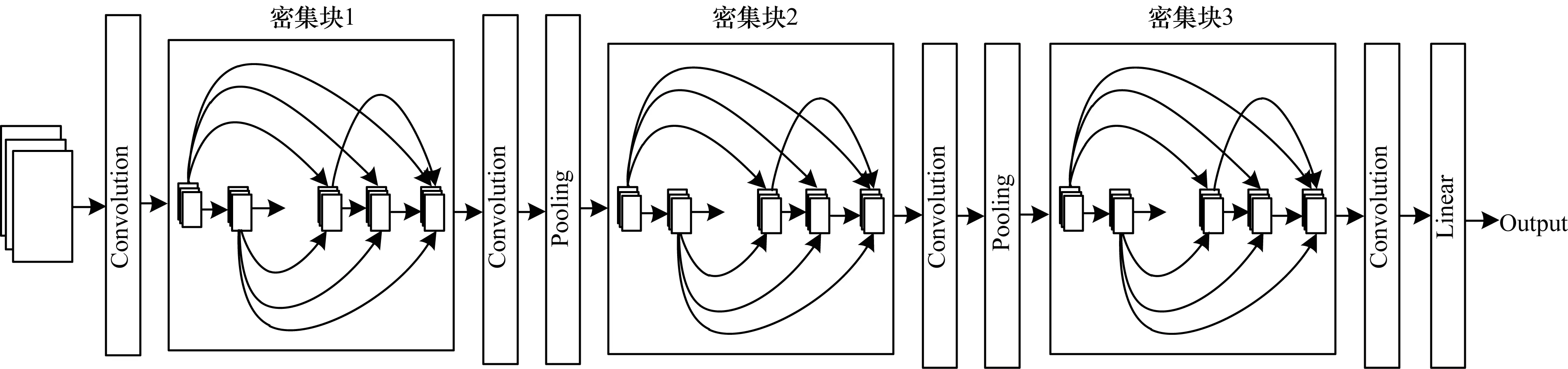
图5 DenseNet-BC网络结构

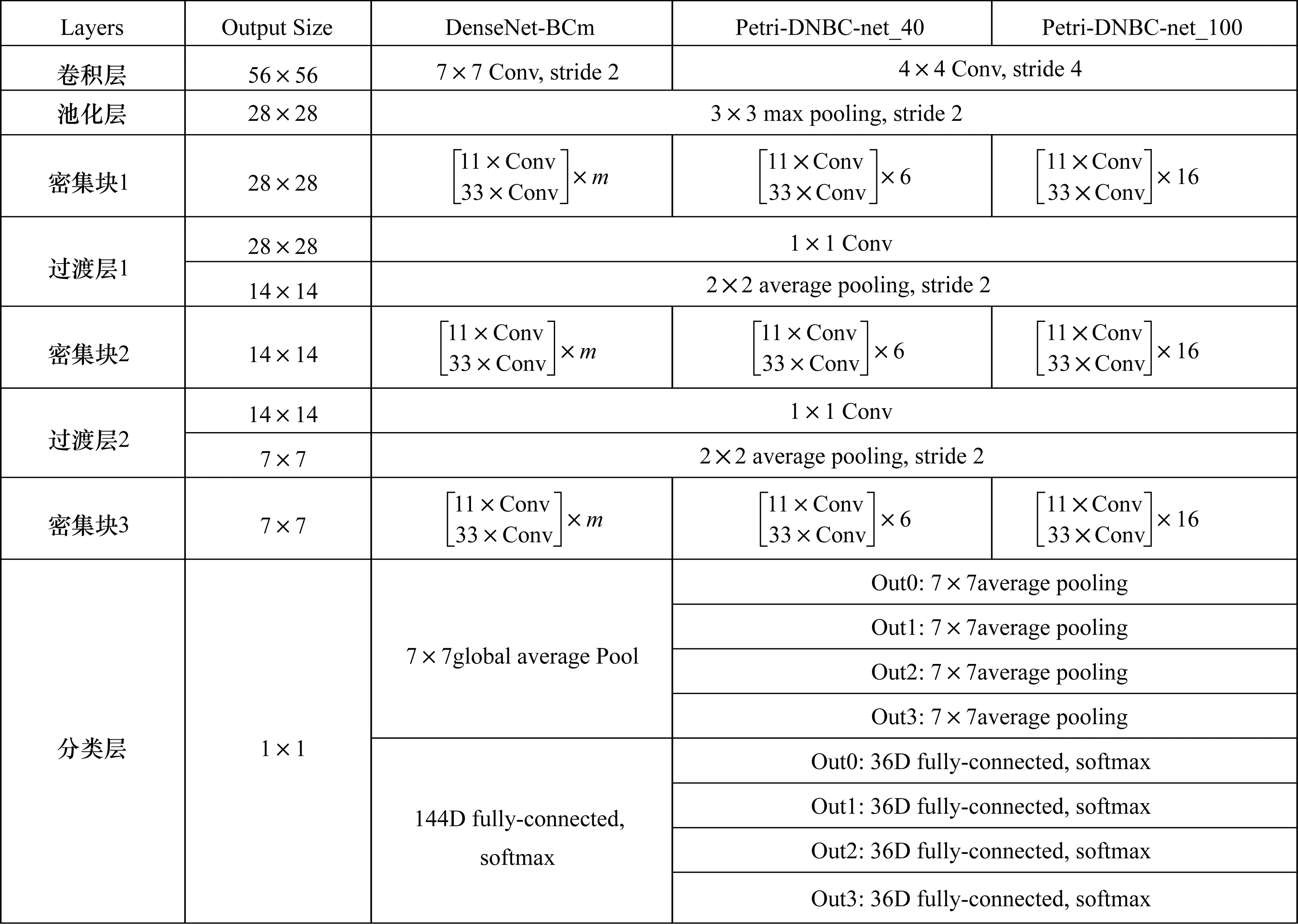
图6 DenseNet-BC网络参数

从图6可以看出,该模型由3个密集块与2个过渡层组成,并将原来的单分类层改为并行的四分类层。

2.4.3 基于Petri网优化的DenseNet-BC

定义4Petri网优化的DenseNet-BC(Petri-DNBC-net)在定义3的条件下还应满足以下条件:

1)∀x∈S∪T,x∩x·≠∅即对元素x的前集与后集相交不为空(网络不为纯网)。

2)t1,t2∈T时,t1和t2不一定处于公平状态。

2.5 活性及超活性对模型的性能评价

2.5.1 活性

根据定义1中的CNE-net,如果对任意C∈R(M0),都存在M′∈R(M),使得M′[t>,则称变迁t是活的。如果t∈T都是活的,则称N为活的Petri网[14]。

2.5.2 超活性

活性用来评判网络是否存在死锁或者陷阱等不足,但是其不能用来评判网络的反应灵敏度。基于此,提出了超活性的概念。

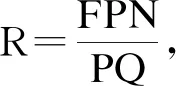
1)在同构系统中,超活性(R)相同时,则灵敏度相同。

2)在异构系统中,比较超活性R1和R2的值,R较大者则灵敏度相对较高。

2.5.3 3种网络结构的超活性比较

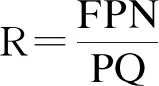
3 实验结果与分析

本文实验基于Win10平台,CPU为Inter(R) Xeon(R) E5-1620 v3 3.5 GHz,内存8 GB,显卡为NVIDIA RTX 2080。

3.1 数据集

在深度学习的训练过程中需要大量的数据来训练构建的网络模型。由于目前没有公开的验证码数据集,本文采用验证码生成器生成4字验证码数据集,在生成验证码的过程中对字符进行不同程度的旋转、扭转、平移、加入噪点及字符重叠等处理[22]。验证码图片大小为60×160,由阿拉伯数字0～9以及小写字母a～z共36类随机组成。通过对生成的验证码图片进行灰度化处理,以提高训练和测试的速度,然后将得到的灰度图片制作成Tensorflow易读取的TFrecords格式的数据集。图7为部分验证码图片。

图7 部分验证码图片

3.2 数据集选择

选择基于框架Tensorflow的实现,在综合比较后,损失函数采用sigmoid交叉熵损失函数,优化器采用AdamOptimizer来使损失函数sigmoid交叉熵最小化,其学习率初始固定为0.000 3,初始训练批次大小为20。在训练过程中还添加了dropout层,能够在一定程度上防止过拟合,其参数值为0.5。图8显示了不同训练集下的准确度。

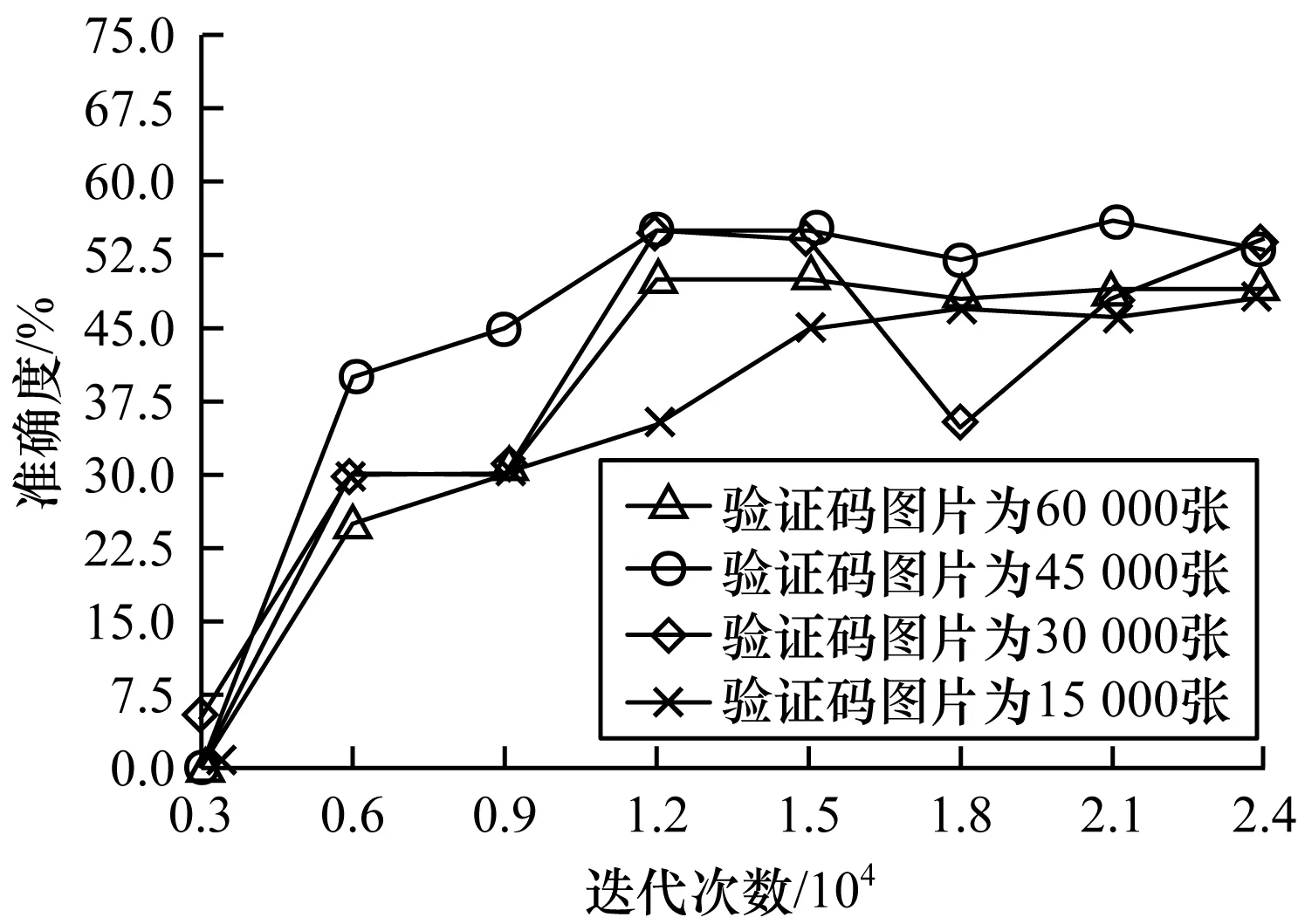
图8 不同训练集的准确度

从图8可以看出,当选用45 000张验证码图片时(其中训练集为40 000张,测试集为5 000张),其准确度最高为55%左右(测试方式为测试10个批次,每个批次为40张,将每个批次的准确度相加再除以10即为最终的准确度),较其余3组数据集性能更为优越。因此,在下文的实验中,TFrecords数据集均采用45 000张图片制作。

3.3 Petri-ANPP-net实验

由Petri-ANPP-net可知,Petri网在结构确定的情况下,其性能由库所P中资源和流关系F上的权函数共同决定。预备实验中的学习率(权函数)与批次大小(资源)是随机设置的,存在较大的局限性,而同时调整2个参数会导致模型变得异常复杂。因此,假设当token发生变化时,权函数W为理想条件,即M[t>M′一定发生。同理,当调整权函数W时,其资源一定满足所有条件即不发生冲突、冲撞等异常情况。

实验1结合预备实验,将初始学习率设为0.000 3,即流关系F的权值设置为0.000 3(这里将0.000 3看成无穷大,资源均能快速通过),设置4组不同批次的对照实验。第1组为10张/批次,第2组为20张/批次,第3组为25张/批次,第4组为30张/批次。在初始库所P0中放置不同的token数量,以测试该系统的最佳token性能。图9显示了不同大小的批次量在不同迭代次数下的准确度。

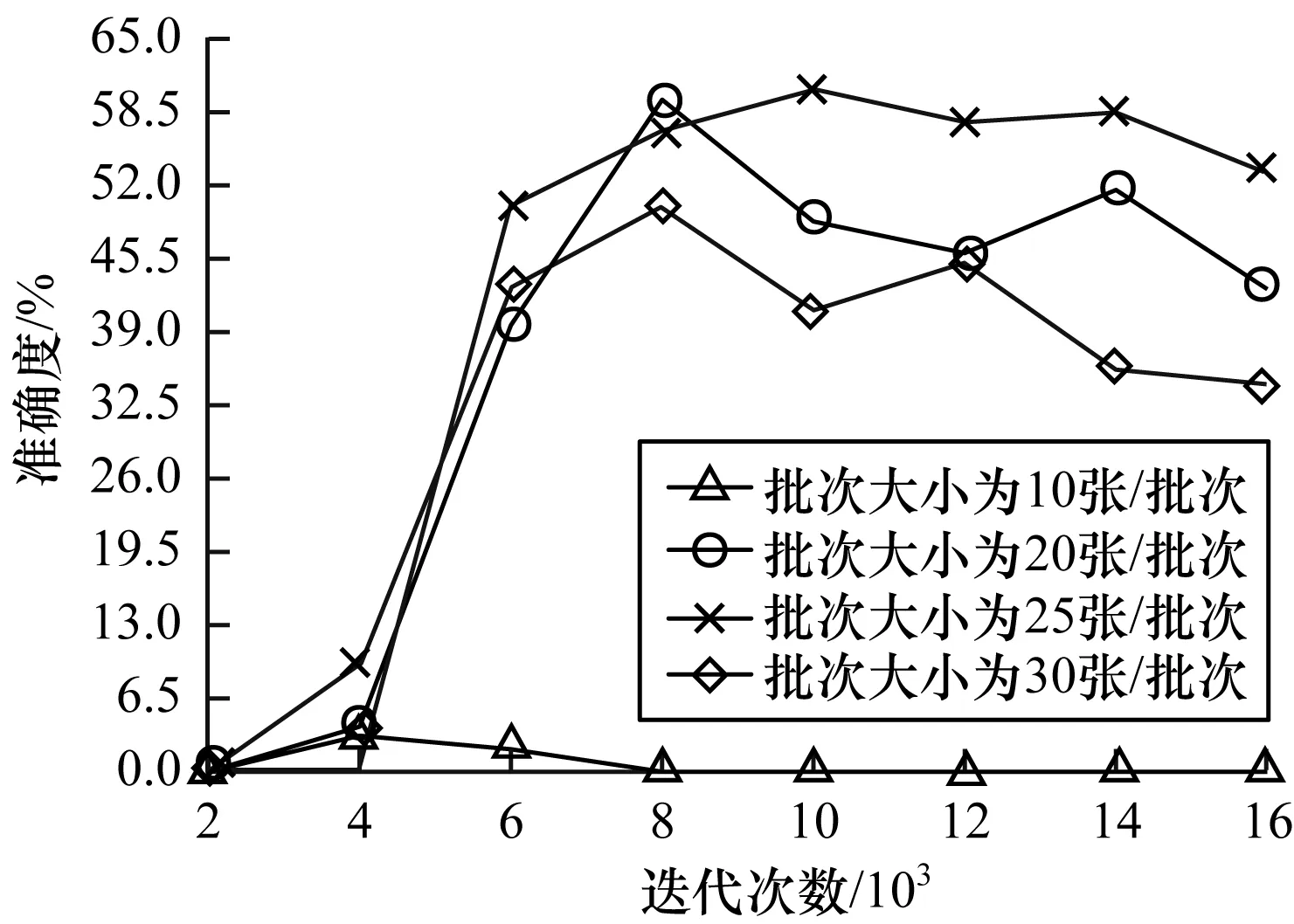
图9 不同大小批次量的准确度

从图9可以看出,批次量太大或太小均会影响系统的整体性能,当批次量为25张/批次时,在该网络结构条件下准确度达到最优,且最优值为60%。

实验2由实验1可知,当批次量设置为25张/批次时,系统所能达到的性能具有最优标准。但是实验1随机固定了初始学习率,不能说明实验1的最高准确度就是该网络结构下的最高值。基于此,在实验1的基础上(即固定批次量为25张/批次),设置4组不同的学习率参数进行对照实验。第1组学习率为0.000 2,第2组学习率为0.000 3,第3组学习率为0.000 4,第4组学习率为0.000 5。图10显示了不同学习率在不同迭代次数下的准确度。

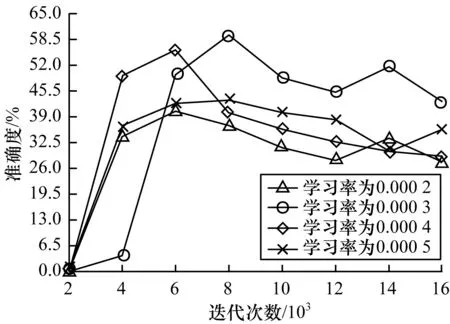
图10 不同学习率的准确度

从图10可以看出,学习率过大或过小均会影响系统整体性能,当学习率为0.000 3时,在该网络结构条件下,准确度达到最优,且最优值为60%(说明实验1随机设置的学习率即为最佳学习率)。

基于Petri-ANPP-net所能达到的准确度最高为60%,与预处理实验中55%相比略有提升。而此时库所中token资源与流关系F均已调整为最佳。由以上实验可知,参数调节能在一定范围内优化系统性能。

3.4 Petri-ANPS-net实验

由Petri-ANPS-net可知,网结构优化后,其性能也会发生改变。为此,设置实验3、实验4两组实验。

实验3为验证不同学习率下Petri网优化结构后模型的准确度,将批次量设置为25张/批次(结合实验1、实验2),进行了4组对比实验。第1组学习率为0.000 1,第2组学习率为0.000 2,第3组学习率为0.000 3,第4组学习率为0.000 4,实验结果如图11所示。

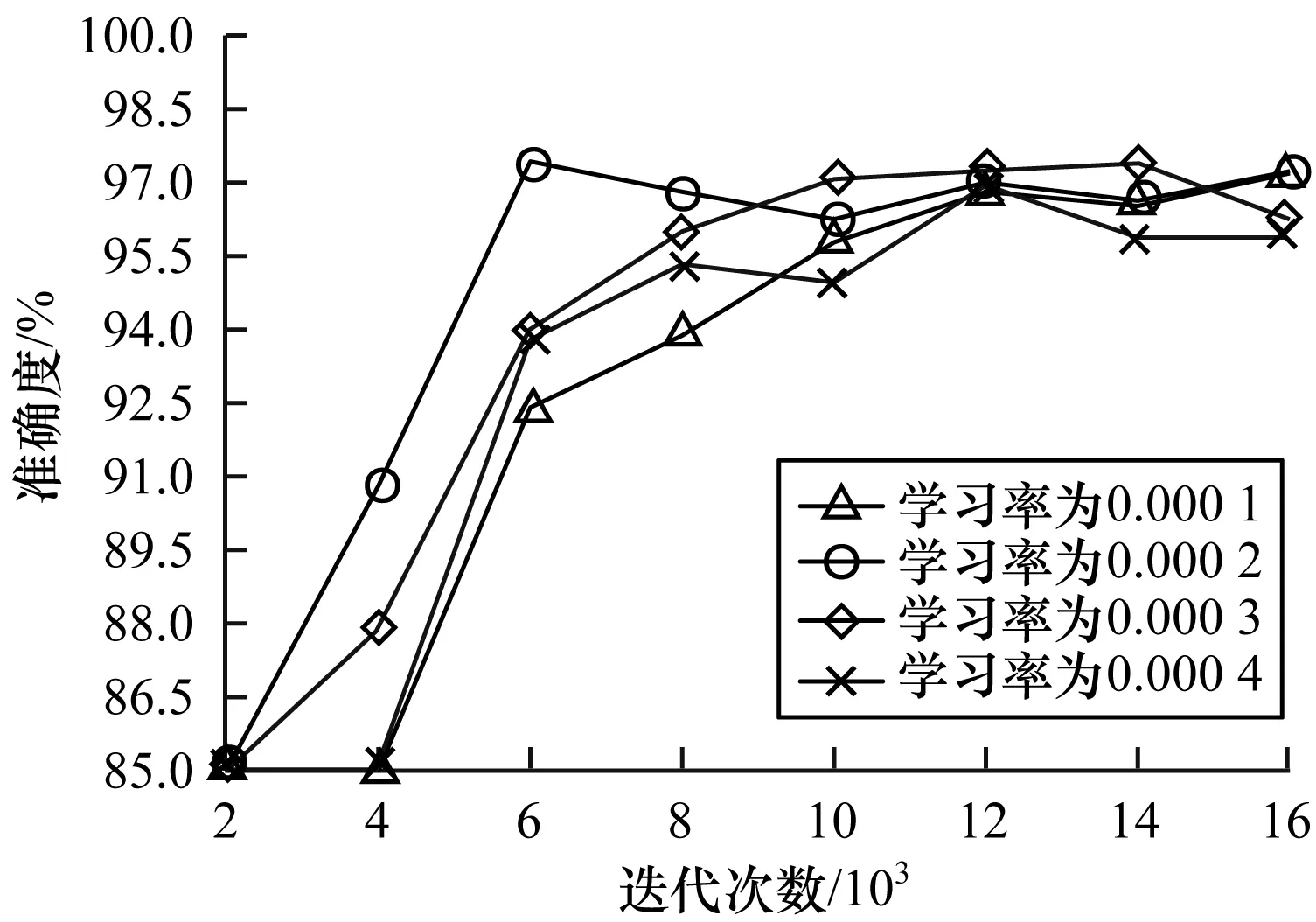
图11 优化结构后不同学习率的准确度

从图11可以看出,在网络结构合理的条件下,准确度将保持较高水平,当学习率为0.000 3时,其最高值相对平稳且略优于其他各组。

实验4为验证不同批次下Petri网优化结构后模型的准确度,将学习率设置为0.000 3(由实验3得),调整批次大小后再进行4组实验。第1组批次大小为20张/批次,第2组为25张/批次,第3组为30张/批次,第4组为40张/批次,优化结构后不同批次下准确度的实验结果如图12所示。

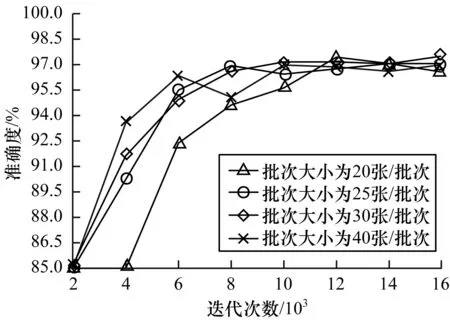
图12 优化结构后不同批次的准确度

从图12可以看出,在网络结构合理的情况下,单一参数在一定范围内变化对准确度影响较小;当学习率为0.000 3、批次大小为30张/批次时,其准确度最高达到了97.50%。

对以上各组实验中不同参数条件下的平均最高准确度进行总结,结果如表3所示。

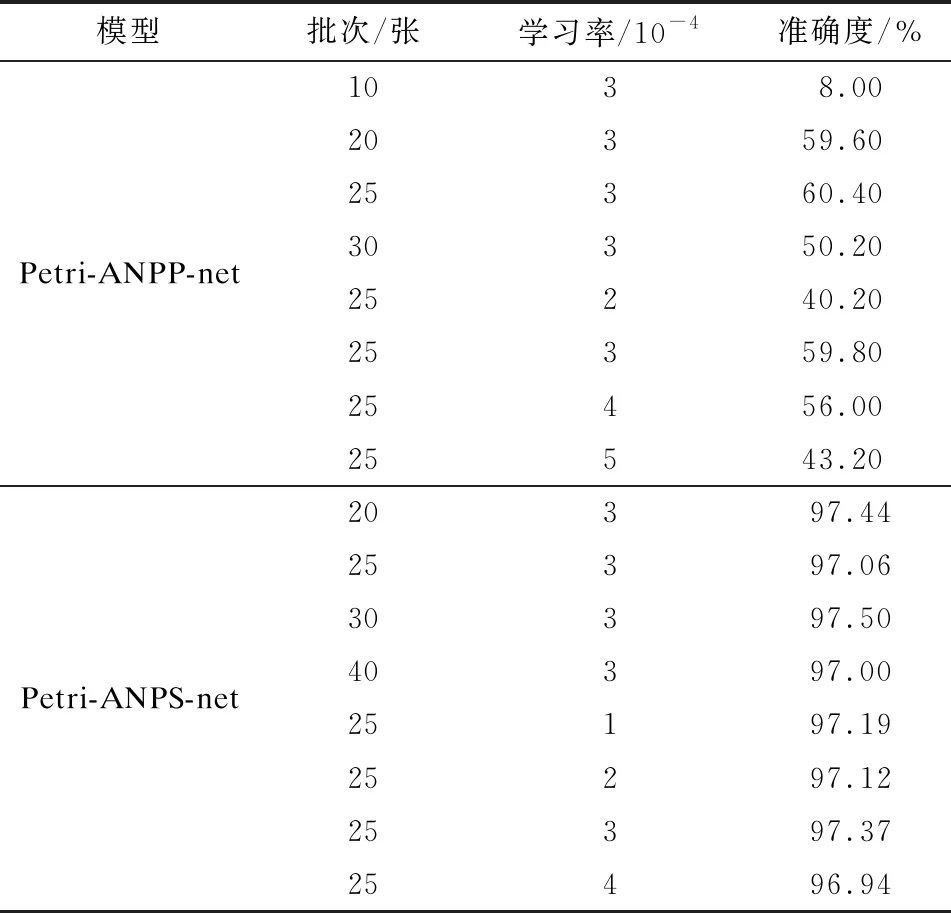
表3 不同参数下的平均最高准确度

从表3可以看出,批次和学习率均能影响模型性能,尤其是一些不合理的参数会导致网络模型失败,在最佳参数条件下,Petri-ANPS-net网络相对于Petri-ANPP-net绝对准确度提升了37.10%,说明网络模型设计是系统成功的关键。

3.5 Petri-DNBC-net实验

由Petri-DNBC-net可知,当网络模型改变后,则网络性质将会发生一定的改变,从而导致网络性能发生改变。

实验5参考Petri-ANPP-net以及Petri-ANPS-net,将验证码大小设置为224×224。经过综合比较后,学习率设置为0.1,偏置值设置为0.000 1,批次大小为64张/批次。在此基础上,设置4组对比实验,第1组网络深度为40,增长率为12%,第2组网络深度为40,增长率为24%,第3组网络深度为100,增长率为12%,第4组网络深度为100,增长率为24%。表4为在各参数条件下Petri-DMBC-net的准确度。

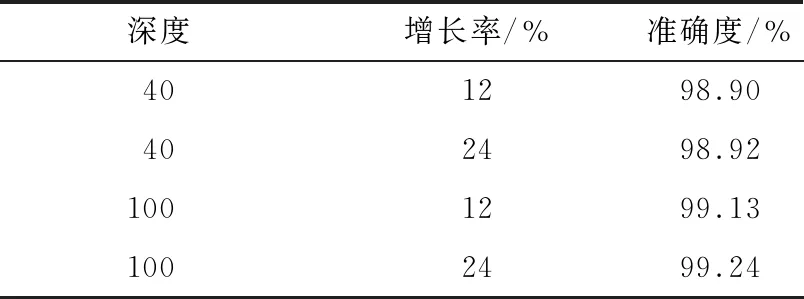
表4 Petri-DNBC-net的准确度

从表4可以看出,当深度和增长率增加后,其准确度会相应增加,当深度为100时,其准确度大于99%。

3.6 超活性对模型的性能评价

由以上实验可知,Petri-DNBC-net的准确度略优于Petri-ANPS-net,且Petri-ANPP-net准确度最低。但是,准确度仅是验证模型综合性能的指标之一。为此,还应考虑超活性对模型性能的影响。

为测试各模型的超活性,选择在不同模型的最高准确度下进行超活性分析,实验结果如表5所示。

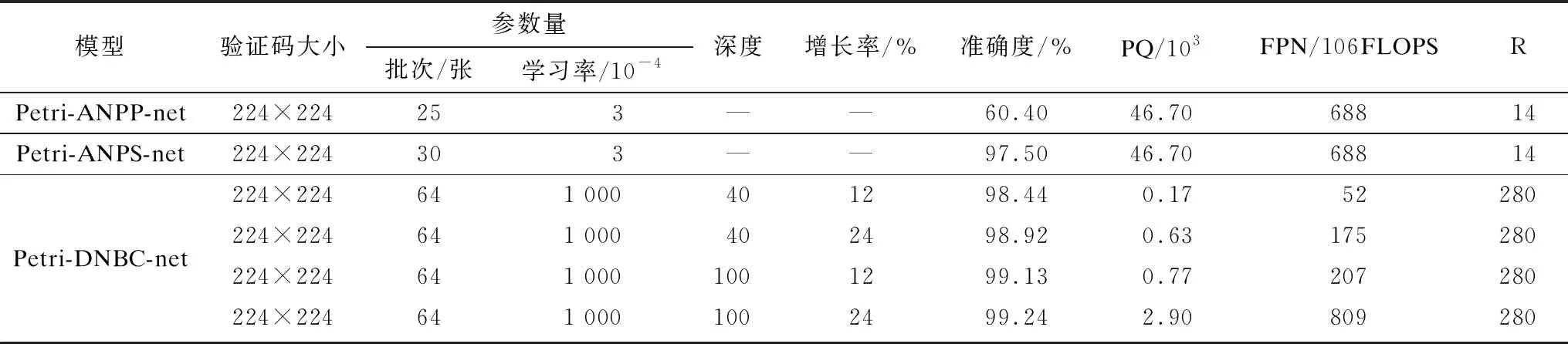
表5 不同模型的性能指标

从表5可以看出:

1)Petri-ANPP-net和Petri-ANPS-net网络的超活性R值相同,说明它们的灵敏度相同,这也验证了同构网络具有相同的PQ、FPN和超活性R值。同时,Petri-ANPP-net的最高准确度为60.40%,而Petri-ANPS-net的最高准确度为97.50%,说明Petri-ANPS-net综合性能远高于Petri-ANPP-net。

2)无论在何种条件下,Petri-DNBC-net的准确度都略高于Petri-ANPS-net。而在超活性方面,Petri-DNBC-net的超活性RD≈280,Petri-ANPS-net的超活性RA≈14。因此,Petri-DNBC-net的灵敏度高于Petri-ANPS-net,且综合性能也优于Petri-ANPS-net网络。

4 结束语

本文利用Petri网理论,基于AlexNet、DenseNet-BC网络得到Petri-ANPP-net、Petri-ANPS-net以及Petri-DNBC-net 3种优化的网络模型,并提出基于Petri网优化的验证码识别方法。基于模型异构性对评判标准产生的影响,提出了超活性概念,其对模型的灵敏度评判具有较高准确性,能够消除异构性从而达到公平评判模型灵敏度的目的。实验结果表明,本文方法能够在一定程度上优化网络模型的结构和参数。下一步将优化卷积核、池化核以及研究学习率与批次大小之间的关系,以提升验证码的安全性。